REGULARIZATION OF NON-NORMAL MATRICES BY GAUSSIAN NOISE—THE BANDED TOEPLITZ AND TWISTED TOEPLITZ CASES

Abstract

We consider the spectrum of additive, polynomially vanishing random perturbations of deterministic matrices, as follows. Let 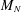$M_{N}$ be a deterministic 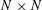$N\times N$ matrix, and let 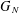$G_{N}$ be a complex Ginibre matrix. We consider the matrix 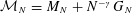${\mathcal{M}}_{N}=M_{N}+N^{-\unicode[STIX]{x1D6FE}}G_{N}$, where 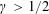$\unicode[STIX]{x1D6FE}>1/2$. With 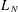$L_{N}$ the empirical measure of eigenvalues of 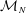${\mathcal{M}}_{N}$, we provide a general deterministic equivalence theorem that ties 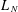$L_{N}$ to the singular values of 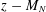$z-M_{N}$, with 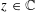$z\in \mathbb{C}$. We then compute the limit of 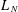$L_{N}$ when 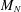$M_{N}$ is an upper-triangular Toeplitz matrix of finite symbol: if 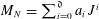$M_{N}=\sum _{i=0}^{\mathfrak{d}}a_{i}J^{i}$ where 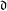$\mathfrak{d}$ is fixed, 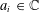$a_{i}\in \mathbb{C}$ are deterministic scalars and 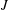$J$ is the nilpotent matrix 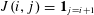$J(i,j)=\mathbf{1}_{j=i+1}$, then 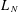$L_{N}$ converges, as 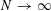$N\rightarrow \infty$, to the law of 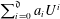$\sum _{i=0}^{\mathfrak{d}}a_{i}U^{i}$ where 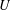$U$ is a uniform random variable on the unit circle in the complex plane. We also consider the case of slowly varying diagonals (twisted Toeplitz matrices), and, when 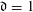$\mathfrak{d}=1$, also of independent and identically distributed entries on the diagonals in 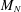$M_{N}$.