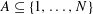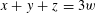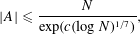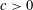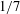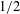Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Browning, T. D.
and
Prendiville, S. M.
2016.
A Transference Approach to a Roth-Type Theorem in the Squares.
International Mathematics Research Notices,
p.
rnw096.
Cwalina, Karol
and
Schoen, Tomasz
2017.
Tight bounds on additive Ramsey-type numbers.
Journal of the London Mathematical Society,
Vol. 96,
Issue. 3,
p.
601.
Hatami, Hamed
Hosseini, Kaave
and
Lovett, Shachar
2018.
Structure of Protocols for XOR Functions.
SIAM Journal on Computing,
Vol. 47,
Issue. 1,
p.
208.
Grochow, Joshua
2018.
New applications of the polynomial method: The cap set conjecture and beyond.
Bulletin of the American Mathematical Society,
Vol. 56,
Issue. 1,
p.
29.
FOX, JACOB
SAH, ASHWIN
SAWHNEY, MEHTAAB
STONER, DAVID
and
ZHAO, YUFEI
2020.
Triforce and corners.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 169,
Issue. 1,
p.
209.
Terry, C.
and
Wolf, J.
2020.
Quantitative structure of stable sets in finite abelian groups.
Transactions of the American Mathematical Society,
Vol. 373,
Issue. 6,
p.
3885.
Schoen, Tomasz
2021.
Improved bound in Roth's theorem on arithmetic progressions.
Advances in Mathematics,
Vol. 386,
Issue. ,
p.
107801.
PRENDIVILLE, SEAN
2022.
Solving equations in dense Sidon sets.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 173,
Issue. 1,
p.
25.
Bloom, Thomas F.
and
Sisask, Olof
2023.
The Kelley–Meka bounds for sets free of
three-term arithmetic progressions.
Essential Number Theory,
Vol. 2,
Issue. 1,
p.
15.
Kelley, Zander
and
Meka, Raghu
2023.
Strong Bounds for 3-Progressions.
p.
933.
Schoen, Tomasz
2024.
Translation-Invariant Equations With at Least Four Variables.
International Mathematics Research Notices,
Vol. 2024,
Issue. 16,
p.
11611.
Shapira, Asaf
2024.
A generalisation of Varnavides’s theorem.
Combinatorics, Probability and Computing,
Vol. 33,
Issue. 6,
p.
724.
Ren, Xiumin
Zhang, Qingqing
and
Zhang, Rui
2024.
Roth-type theorem for quadratic system in Piatetski-Shapiro primes.
Journal of Number Theory,
Vol. 257,
Issue. ,
p.
1.
Peluse, Sarah
2024.
Surveys in Combinatorics 2024.
p.
159.
Schoen, Tomasz
2025.
A note on sumsets of progression-free sets.
The Ramanujan Journal,
Vol. 68,
Issue. 1,