Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Holmes, David
2019.
Torsion points and height jumping in higher-dimensional families of abelian varieties.
International Journal of Number Theory,
Vol. 15,
Issue. 09,
p.
1801.
Burgos Gil, José Ignacio
Holmes, David
and
de Jong, Robin
2019.
Positivity of the Height Jump Divisor.
International Mathematics Research Notices,
Vol. 2019,
Issue. 7,
p.
2044.
Brosnan, Patrick
and
Pearlstein, Gregory
2019.
Jumps in the Archimedean height.
Duke Mathematical Journal,
Vol. 168,
Issue. 10,
Jespers, Michiel
and
de Jong, Robin
2020.
Chern–Weil Theory for Line Bundles with the Family Arakelov Metric.
Michigan Mathematical Journal,
Vol. 69,
Issue. 1,
Burgos Gil, Jose Ignacio
Goswami, Souvik
and
Pearlstein, Gregory
2022.
Height pairing on higher cycles and mixed Hodge structures.
Proceedings of the London Mathematical Society,
Vol. 125,
Issue. 1,
p.
61.
Song, Yinchong
2023.
Asymptotic behavior of the Zhang–Kawazumi's φ-invariants.
Advances in Mathematics,
Vol. 435,
Issue. ,
p.
109349.
Botero, Ana María
Burgos Gil, José Ignacio
Holmes, David
and
de Jong, Robin
2024.
Rings of Siegel–Jacobi forms of bounded relative index are not finitely generated.
Duke Mathematical Journal,
Vol. 173,
Issue. 12,
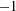 $-1$
.
$-1$
.