Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T16:56:55.316Z Has data issue: false hasContentIssue false
  • English
  • Français

THE SPACE OF HYPERKÄHLER METRICS ON A 4-MANIFOLD WITH BOUNDARY

Part of: Partial differential equations on manifolds; differential operators Global differential geometry

Published online by Cambridge University Press:  01 March 2017

JOEL FINE ,
JASON D. LOTAY  and
MICHAEL SINGER
JOEL FINE
Affiliation:
Départment de mathématique, Université libre de Bruxelles (ULB), CP 218, Boulevard du Triomphe, B-1050 Bruxelles, Belgium; joel.fine@ulb.ac.be
JASON D. LOTAY
Affiliation:
Department of Mathematics, University College, London WC1E 6BT, UK; j.lotay@ucl.ac.uk, michael.singer@ucl.ac.uk
MICHAEL SINGER
Affiliation:
Department of Mathematics, University College, London WC1E 6BT, UK; j.lotay@ucl.ac.uk, michael.singer@ucl.ac.uk

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 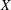$X$ be a compact 4-manifold with boundary. We study the space of hyperkähler triples 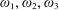$\unicode[STIX]{x1D714}_{1},\unicode[STIX]{x1D714}_{2},\unicode[STIX]{x1D714}_{3}$ on 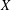$X$, modulo diffeomorphisms which are the identity on the boundary. We prove that this moduli space is a smooth infinite-dimensional manifold and describe the tangent space in terms of triples of closed anti-self-dual 2-forms. We also explore the corresponding boundary value problem: a hyperkähler triple restricts to a closed framing of the bundle of 2-forms on the boundary; we identify the infinitesimal deformations of this closed framing that can be filled in to hyperkähler deformations of the original triple. Finally we study explicit examples coming from gravitational instantons with isometric actions of 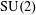$\text{SU}(2)$.

MSC classification

Primary: 53C26: Hyper-Kähler and quaternionic Kähler geometry, “special” geometry 58J32: Boundary value problems on manifolds
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 5 , 2017 , e6
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2017

References

Atiyah, M. F. and Hitchin, N. J., The Geometry and Dynamics of Magnetic Monopoles, M. B. Porter Lectures (Princeton University Press, Princeton, NJ, 1988).Google Scholar
Atiyah, M. F., Hitchin, N. J. and Singer, I. M., ‘Self-duality in four-dimensional Riemannian geometry’, Proc. R. Soc. Lond. Ser. A 362 (1978), 425–461.Google Scholar
Bär, C. and Ballmann, W., ‘Guide to boundary value problems for Dirac-type operators’, inArbeitstagung Bonn 2013, Progress in Mathematics, 319 , 43–80.Google Scholar
Bartnik, R. A. and Chrusciel, P. T., ‘Boundary value problems for Dirac-type equations’, J. Reine Angew. Math. 579 (2005), 13–73.Google Scholar
Biquard, O., ‘Métriques autoduales sur la boule’, Invent. Math. 148 (2002), 545–607.Google Scholar
Bryant, R. L., ‘Nonembedding and nonextension results in special holonomy’, inThe Many Facets of Geometry (Oxford University Press, Oxford, 2010), 346–367.CrossRefGoogle Scholar
Cartan, É., La géometrie des espaces de Riemann, Mémorial des Sciences Mathematiques, Fasc. IX (Gauthier-Villars, Paris, 1925).Google Scholar
Dancer, A. S., ‘A family of hyperkähler manifolds’, Q. J. Math. 45 (1994), 463–478.Google Scholar
Donaldson, S. K., ‘Two-forms on four-manifolds and elliptic equations’, inInspired by S. S. Chern, Nankai Tracts in Mathematics, 11 (World Scientific Publishing, Hackensack, NJ, 2006), 153–172.Google Scholar
Ebin, D., ‘The manifold of Riemannian metrics’, Proc. Sympos. Pure Math. 15 (1970), 11–40.CrossRefGoogle Scholar
Ebin, D. and Marsden, J., ‘Groups of diffeomorphisms and the motion of an incompressible fluid’, Ann. of Math. (2) 92 (1970), 102–163.Google Scholar
Gibbons, G. and Pope, C., ‘The positive action conjecture and asymptotically Euclidean metrics in quantum gravity’, Commun. Math. Phys. 66 (1979), 267–290.CrossRefGoogle Scholar
Gromov, M., Partial Differential Relations (Springer, Berlin, 1986).CrossRefGoogle Scholar
Hitchin, N., ‘Hyper-Kähler manifolds’, Séminaire Bourbaki, Vol. 1991/92, Astérisque, 206 (1992), Exp. No. 748, 3, 137–166.Google Scholar
LeBrun, C., ‘Spaces of complex geodesics and related structures’, DPhil, University of Oxford, 1980. Available at http://ora.ox.ac.uk/objects/uuid:e29dd99c-0437-4956-8280-89dda76fa3f8.Google Scholar
LeBrun, C., ‘On complete quaternionic-Kähler manifolds’, Duke Math. J. 63 (1991), 723–743.CrossRefGoogle Scholar
Schwarz, G., Hodge Decomposition—A Method for Solving Boundary Value Problems, (Springer, Berlin, 1995).Google Scholar
Taylor, M. E., Partial Differential Equations, Vol. 1, Applied Mathematical Sciences, 115 (Springer, New York, 1996).Google Scholar
Tromba, A. J., Teichmüller Theory in Riemannian Geometry, Lectures in Mathematics ETH Zürich (Birkhäuser, Basel, 1992).Google Scholar