Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T22:21:33.427Z Has data issue: false hasContentIssue false
  • English
  • Français

STABILITY, COHOMOLOGY VANISHING, AND NONAPPROXIMABLE GROUPS

Part of: Locally compact groups and their algebras

Published online by Cambridge University Press:  30 March 2020

MARCUS DE CHIFFRE ,
LEV GLEBSKY ,
ALEXANDER LUBOTZKY  and
ANDREAS THOM
MARCUS DE CHIFFRE
Affiliation:
TU Dresden, Germany; marcus@dechiffre.dk
LEV GLEBSKY
Affiliation:
L.G., Universidad Autónoma de San Luis Potosí, México; glebsky@cactus.iico.uaslp.mx
ALEXANDER LUBOTZKY
Affiliation:
A.L., Hebrew University, Israel; alex.lubotzky@mail.huji.ac.il
ANDREAS THOM
Affiliation:
TU Dresden, Germany; andreas.thom@tu-dresden.de

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Several well-known open questions (such as: are all groups sofic/hyperlinear?) have a common form: can all groups be approximated by asymptotic homomorphisms into the symmetric groups 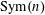$\text{Sym}(n)$ (in the sofic case) or the finite-dimensional unitary groups 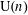$\text{U}(n)$ (in the hyperlinear case)? In the case of 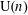$\text{U}(n)$, the question can be asked with respect to different metrics and norms. This paper answers, for the first time, one of these versions, showing that there exist finitely presented groups which are not approximated by 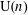$\text{U}(n)$ with respect to the Frobenius norm 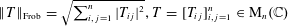$\Vert T\Vert _{\text{Frob}}=\sqrt{\sum _{i,j=1}^{n}|T_{ij}|^{2}},T=[T_{ij}]_{i,j=1}^{n}\in \text{M}_{n}(\mathbb{C})$. Our strategy is to show that some higher dimensional cohomology vanishing phenomena implies stability, that is, every Frobenius-approximate homomorphism into finite-dimensional unitary groups is close to an actual homomorphism. This is combined with existence results of certain nonresidually finite central extensions of lattices in some simple 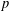$p$-adic Lie groups. These groups act on high-rank Bruhat–Tits buildings and satisfy the needed vanishing cohomology phenomenon and are thus stable and not Frobenius-approximated.

MSC classification

Primary: 22D10: Unitary representations of locally compact groups
Secondary: 39B82: Stability, separation, extension, and related topics
Type
Topology
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e18
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2020

References

Abramenko, P. and Brown, K. S., ‘Theory and applications’, inBuildings, Graduate Texts in Mathematics, 248 (Springer, New York, 2008).CrossRefGoogle Scholar
Bhatia, R., Matrix Analysis, Graduate Texts in Mathematics, 169 (Springer, New York, 1997).CrossRefGoogle Scholar
Arzhantseva, G., ‘Asymptotic approximations of finitely generated groups’, inExtended Abstracts Fall 2012—Automorphisms of Free Groups, Trends Math. Res. Perspect. CRM Barc., 1 (Springer, Cham, 2014), 7–15.Google Scholar
Arzhantseva, G. and Păunescu, L., ‘Almost commuting permutations are near commuting permutations’, J. Funct. Anal. 269(3) (2015), 745–757.CrossRefGoogle Scholar
Bader, U. and Nowak, P. W., ‘Cohomology of deformations’, J. Topol. Anal. 7(1) (2015), 81–104.CrossRefGoogle Scholar
Ballmann, W. and Światkowski, J., ‘On L 2 -cohomology and property (T) for automorphism groups of polyhedral cell complexes’, Geom. Funct. Anal. 7(4) (1997), 615–645.CrossRefGoogle Scholar
Baumslag, G. and Solitar, D., ‘Some two-generator one-relator non-Hopfian groups’, Bull. Amer. Math. Soc. 68 (1962), 199–201.CrossRefGoogle Scholar
Becker, O., Lubotzky, A. and Thom, A., ‘Stability and invariant random subgroups’, Duke Math. J. 168(12) (2019), 2207–2234.CrossRefGoogle Scholar
Bekka, B., de la Harpe, P. and Valette, A., Kazhdan’s Property (T), New Mathematical Monographs, 11 (Cambridge University Press, Cambridge, 2008).CrossRefGoogle Scholar
Blackadar, B. and Kirchberg, E., ‘Generalized inductive limits of finite-dimensional C ∗ -algebras’, Math. Ann. 307(3) (1997), 343–380.CrossRefGoogle Scholar
Borel, A., ‘Stable real cohomology of arithmetic groups’, Ann. Sci. Éc. Norm. Supér. (4) 7(1974) (1975), 235–272.CrossRefGoogle Scholar
Borel, A. and Wallach, N., Continuous Cohomology, Discrete Subgroups, and Representations of Reductive Groups, 2nd edn, Mathematical Surveys and Monographs, 67 (American Mathematical Society, Providence, RI, 2000).CrossRefGoogle Scholar
Brown, K. S., Cohomology of Groups, Graduate Texts in Mathematics, 87 (Springer, New York, 1994), Corrected reprint of the 1982 original.Google Scholar
Burger, M., Ozawa, N. and Thom, A., ‘On Ulam stability’, Israel J. Math. 193(1) (2013), 109–129.CrossRefGoogle Scholar
Carrion, J., Dadarlat, M. and Eckhardt, C., ‘On groups with quasidiagonal C ∗ -algebras’, J. Funct. Anal. 265(1) (2013), 135–152.CrossRefGoogle Scholar
Connes, A., ‘Classification of injective factors. Cases II 1II ∞III 𝜆 𝜆̸ = 1’, Ann. of Math. (2) 104(1) (1976), 73–115.CrossRefGoogle Scholar
De Chiffre, M., Ozawa, N. and Thom, A., ‘Operator algebraic approach to inverse and stability theorems for amenable groups’, Mathematika 65(1) (2019), 98–118.CrossRefGoogle Scholar
Deligne, P., ‘Extensions centrales non résiduellement finies de groupes arithmétiques’, C. R. Acad. Sci. Paris Sér. A-B 287(4) (1978), A203–A208. (French, with English summary).Google Scholar
Deodhar, V. V., ‘On central extensions of rational points of algebraic groups’, Bull. Amer. Math. Soc. 81 (1975), 573–575.CrossRefGoogle Scholar
Dymara, J. and Januszkiewicz, T., ‘New Kazhdan groups’, Geom. Dedicata 80(1–3) (2000), 311–317.CrossRefGoogle Scholar
Dymara, J. and Januszkiewicz, T., ‘Cohomology of buildings and their automorphism groups’, Invent. Math. 150(3) (2002), 579–627.CrossRefGoogle Scholar
Exel, R. and Loring, T., ‘Almost commuting unitary matrices’, Proc. Amer. Math. Soc. 106(4) (1989), 913–915.CrossRefGoogle Scholar
Fritz, T., ‘On infinite-dimensional state spaces’, J. Math. Phys. 54(5)052107 (2013).CrossRefGoogle Scholar
Garland, H., ‘p-adic curvature and the cohomology of discrete subgroups of p-adic groups’, Ann. of Math. (2) 97 (1973), 375–423.CrossRefGoogle Scholar
Glebsky, L. and Rivera, L. M., ‘Sofic groups and profinite topology on free groups’, J. Algebra 320(9) (2008), 3512–3518.CrossRefGoogle Scholar
Gromov, M., ‘Endomorphisms of symbolic algebraic varieties’, J. Eur. Math. Soc. 1(2) (1999), 109–197.CrossRefGoogle Scholar
Grove, K., Karcher, H. and Ruh, E. A., ‘Jacobi fields and Finsler metrics on compact Lie groups with an application to differentiable pinching problems’, Math. Ann. 211 (1974), 7–21.CrossRefGoogle Scholar
Gundert, A. and Wagner, U., ‘On eigenvalues of random complexes’, Israel J. Math. 216(2) (2016), 545–582.CrossRefGoogle Scholar
Kazhdan, D., ‘On 𝜀-representations’, Israel J. Math. 43(4) (1982), 315–323.CrossRefGoogle Scholar
Kropholler, P. H., ‘Baumslag–Solitar groups and some other groups of cohomological dimension two’, Comment. Math. Helv. 65(4) (1990), 547–558.CrossRefGoogle Scholar
Lubotzky, A., ‘High dimensional expanders’, Proc. Int. Cong. Math. 1 (2018), 705–730.Google Scholar
Lubotzky, A. and Oppenheim, I., ‘Non $p$-norm approximated groups’, J. d’Anal. Math., to appear.Google Scholar
Moore, C. C., ‘Group extensions of p-adic and adelic linear groups’, Publ. Math. Inst. Hautes Etudes Sci. 35 (1968), 157–222.CrossRefGoogle Scholar
Nikolov, N., Schneider, J. and Thom, A., ‘Some remarks on finitarily approximated groups’, J. Éc. Polytech. Math. 5 (2018), 239–258.CrossRefGoogle Scholar
Oppenheim, I., ‘Vanishing of cohomology and property (T) for groups acting on weighted simplicial complexes’, Groups Geom. Dyn. 9(1) (2015), 67–101.CrossRefGoogle Scholar
Ozawa, N., Rørdam, M. and Sato, Y., ‘Elementary amenable groups are quasidiagonal’, Geom. Funct. Anal. 25(1) (2015), 307–316.CrossRefGoogle Scholar
Pansu, P., ‘Formules de Matsushima, de Garland et propriété (T) pour des groupes agissant sur des espaces symétriques ou des immeubles’, Bull. Soc. Math. France 126(1) (1998), 107–139. (French, with English and French summaries).CrossRefGoogle Scholar
Pestov, V. G., ‘Hyperlinear and sofic groups: a brief guide’, Bull. Symb. Logic 14(4) (2008), 449–480.CrossRefGoogle Scholar
Platonov, V. and Rapinchuk, A. S., Algebraic Groups and Number Theory, Pure and Applied Mathematics 139 (Academic Press, Inc., Boston, MA, 1994).CrossRefGoogle Scholar
Prasad, G., ‘Deligne’s topological central extension is universal’, Adv. Math. 181(1) (2004), 160–164.CrossRefGoogle Scholar
Prasad, G. and Rapinchuk, A. S., ‘Computation of the metaplectic kernel’, Publ. Math. Inst. Hautes Etudes Sci. 84 (1997), 91–187.CrossRefGoogle Scholar
Rădulescu, F., ‘The von Neumann algebra of the non-residually finite Baumslag group 〈a, b|ab 3a -1 = b 2〉 embeds into R 𝜔’, inHot Topics in Operator Theory, Theta Ser. Adv. Math., 9 (Theta, Bucharest, 2008), 173–185.Google Scholar
Raghunathan, M. S., ‘Torsion in cocompact lattices in coverings of Spin(2,  n)’, Math. Ann. 266(4) (1984), 403–419.CrossRefGoogle Scholar
Raghunathan, M. S., ‘Corrigendum: “Torsion in cocompact lattices in coverings of Spin(2, n)”’, Math. Ann. 303(3) (1995), 575–578.CrossRefGoogle Scholar
Rapinchuk, A. S., ‘On the congruence subgroup problem for algebraic groups’, Dokl. Akad. Nauk SSSR 306(6) (1989), 1304–1307 (Russian); English transl., Soviet Math. Dokl. 39 (1989), no. 3, 618–621.Google Scholar
Rudin, W., Functional Analysis, 2nd edn, International Series in Pure and Applied Mathematics (McGraw-Hill, Inc., New York, 1991).Google Scholar
Tikuisis, A., White, S. and Winter, W., ‘Quasidiagonality of nuclear C ∗ -algebras’, Ann. of Math. (2) 185(1) (2017), 229–284.CrossRefGoogle Scholar
Thom, A., ‘Finitary approximations of groups and their applications’, Proc. Int. Cong. Math. 2 (2018), 1775–1796.Google Scholar
Thom, A., ‘Examples of hyperlinear groups without factorization property’, Groups Geom. Dyn. 4(1) (2010), 195–208.CrossRefGoogle Scholar
Toledo, D., ‘Projective varieties with non-residually finite fundamental group’, Publ. Math. Inst. Hautes Etudes Sci. 77 (1993), 103–119.CrossRefGoogle Scholar
Tomanov, G., ‘On the congruence-subgroup problem for some anisotropic algebraic groups over number fields’, J. Reine Angew. Math. 402 (1989), 138–152.Google Scholar
Turing, A. M., ‘Finite approximations to Lie groups’, Ann. of Math. (2) 39(1) (1938), 105–111.CrossRefGoogle Scholar
Ulam, S., A Collection of Mathematical Problems, Interscience Tracts in Pure and Applied Mathematics, 8 (Interscience Publishers, New York–London, 1960).Google Scholar
Voiculescu, D., ‘Asymptotically commuting finite rank unitary operators without commuting approximants’, Acta Sci. Math. (Szeged) 45(1–4) (1983), 429–431.Google Scholar
Żuk, A., ‘Property (T) and Kazhdan constants for discrete groups’, Geom. Funct. Anal. 13(3) (2003), 643–670.CrossRefGoogle Scholar