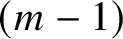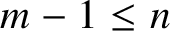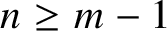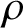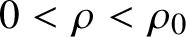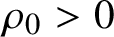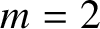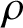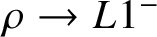1 Introduction
1.1 An Informal Introduction
A voting method or social choice function with m candidates and n voters is a function
From the social choice theory perspective, the input of the function f is a list of votes of n people who are choosing between m candidates. Each of the m candidates is labelled by the integers ![]() $1,\ldots ,m$. If the votes are
$1,\ldots ,m$. If the votes are ![]() $x\in \{1,\ldots ,m\}^{n}$, then
$x\in \{1,\ldots ,m\}^{n}$, then ![]() $x_{i}$ denotes the vote of person
$x_{i}$ denotes the vote of person ![]() $i\in \{1,\ldots ,n\}$ for candidate
$i\in \{1,\ldots ,n\}$ for candidate ![]() $x_{i}\in \{1,\ldots ,m\}$. Given the votes
$x_{i}\in \{1,\ldots ,m\}$. Given the votes ![]() $x\in \{1,\ldots ,m\}^{n}$,
$x\in \{1,\ldots ,m\}^{n}$, ![]() $f(x)$ is interpreted as the winner of the election.
$f(x)$ is interpreted as the winner of the election.
It is both natural and desirable to find a voting method whose output is most likely to be unchanged after votes are randomly altered. One could imagine that malicious third parties or miscounting of votes might cause random vote changes, so we desire a voting method f whose output is stable to such changes. In addition to voting motivations, finding a voting method that is stable to noise has applications to the unique games conjecture [Reference Khot, Kindler, Mossel and O’DonnellKKMO07, Reference Mossel, O’Donnell and OleszkiewiczMOO10, Reference Khot and MoshkovitzKM16], to semidefinite programming algorithms such as MAX-CUT [Reference Khot, Kindler, Mossel and O’DonnellKKMO07, Reference Isaksson and MosselIM12], to learning theory [Reference Feldman, Guruswami, Raghavendra and WuFGRW12], etc. For some surveys on this and related topics, see [Reference O’DonnellO’D, Reference KhotKho, Reference HeilmanHei20].
The output of a constant function f is never altered by changes to the votes. Also, if the function f only depends on one of its n inputs, then the output of f is rarely changed by independent random changes to each of the votes. In these cases, the function f is rather ‘undemocratic’ from the perspective of social choice theory. In the case of a constant function, the outcome of the election does not depend at all on the votes. In the case of a function that only depends on one of its inputs, the outcome of the election only depends on one voter (so f is called a dictatorship function).
Among ‘democratic’ voting methods, it was conjectured in [Reference Khot, Kindler, Mossel and O’DonnellKKMO07] and proven in [Reference Mossel, O’Donnell and OleszkiewiczMOO10] that the majority voting method is the voting method that best preserves the outcome of the election. The following is an informal statement of the main result of [Reference Mossel, O’Donnell and OleszkiewiczMOO10].
Theorem 1.1 Majority Is Stablest, Informal Version [Reference Mossel, O’Donnell and OleszkiewiczMOO10, Theorem 4.4]
Suppose that we run an election with a large number n of voters and ![]() $m=2$ candidates. We make the following assumptions about voter behavior and about the election method.
$m=2$ candidates. We make the following assumptions about voter behavior and about the election method.
• Voters cast their votes randomly and independently, with equal probability of voting for either candidate.
• Each voter has a small influence on the outcome of the election. (That is, all influences from Equation 5 are small for the voting method.)
• Each candidate has an equal chance of winning the election.
Under these assumptions, the majority function is the voting method that best preserves the outcome of the election, when votes have been corrupted independently each with probability less than ![]() $1/2$.
$1/2$.
We say a vote ![]() $x_{i}\in \{1,2\}$ is corrupted with probability
$x_{i}\in \{1,2\}$ is corrupted with probability ![]() $0<\delta <1$ when, with probability
$0<\delta <1$ when, with probability ![]() $\delta $, the vote
$\delta $, the vote ![]() $x_{i}$ is changed to a uniformly random element of
$x_{i}$ is changed to a uniformly random element of ![]() $\{1,2\}$, and with probability
$\{1,2\}$, and with probability ![]() $1-\delta $, the vote
$1-\delta $, the vote ![]() $x_{i}$ is unchanged.
$x_{i}$ is unchanged.
For a formal statement of Theorem 1.1, see Theorem 1.8 below.
The primary interest of the authors of [Reference Khot, Kindler, Mossel and O’DonnellKKMO07] in Theorem 1.1 was proving optimal hardness of approximation for the MAX-CUT problem. In the MAX-CUT problem, we are given a finite undirected graph on n vertices, and the objective of the problem is to find a partition of the vertices of the graph into two sets that maximises the number of edges going between the two sets. The MAX-CUT problem is MAX-SNP hard, i.e. if ![]() $P\neq NP$, there is no polynomial time (in n) approximation scheme for this problem. Nevertheless, there is a randomised polynomial time algorithm [Reference Goemans and WilliamsonGW95] that achieves, in expectation, at least
$P\neq NP$, there is no polynomial time (in n) approximation scheme for this problem. Nevertheless, there is a randomised polynomial time algorithm [Reference Goemans and WilliamsonGW95] that achieves, in expectation, at least ![]() $.87856\ldots $ times the maximum value of the MAX-CUT problem. This algorithm uses semidefinite programming. Also, the exact expression for the
$.87856\ldots $ times the maximum value of the MAX-CUT problem. This algorithm uses semidefinite programming. Also, the exact expression for the ![]() $.87856\ldots $ constant is
$.87856\ldots $ constant is
 $$ \begin{align*} \min_{-1\leq\rho\leq 1}\frac{2}{\pi}\frac{\arccos(\rho)}{1-\rho}=.87856\ldots \end{align*} $$
$$ \begin{align*} \min_{-1\leq\rho\leq 1}\frac{2}{\pi}\frac{\arccos(\rho)}{1-\rho}=.87856\ldots \end{align*} $$ The authors of [Reference Khot, Kindler, Mossel and O’DonnellKKMO07] showed that, if the Unique Games Conjecture is true, then Theorem 1.1 implies that the Goemans-Williamson algorithm’s .87856![]() $\ldots $ constant of approximation cannot be increased. Assuming the validity of the Unique Games Conjecture is a fairly standard in complexity theory, though the conjecture remains open. See [Reference O’DonnellO’D, Reference KhotKho] and the references therein for more discussion on this conjecture, and see [Reference Khot, Minzer and SafraKMS18] for some recent significant progress.
$\ldots $ constant of approximation cannot be increased. Assuming the validity of the Unique Games Conjecture is a fairly standard in complexity theory, though the conjecture remains open. See [Reference O’DonnellO’D, Reference KhotKho] and the references therein for more discussion on this conjecture, and see [Reference Khot, Minzer and SafraKMS18] for some recent significant progress.
Theorem 1.1 (i.e. Theorem 1.8) gives a rather definitive statement on the two candidate voting method that is most stable to corruption of votes. Moreover, the applcation of Theorem 1.1 gives a complete understanding of the optimal algorithm for solving MAX-CUT, assuming the Unique Games Conjecture. Unfortunately, the proof of Theorem 1.1 says nothing about elections with ![]() $m>2$ candidates. Moreover, Theorem 1.1 fails to prove optimality of the Frieze-Jerrum [Reference Frieze and JerrumFJ95] semidefinite programming algorithm for the MAX-m-CUT problem. In the MAX-m-CUT problem, we are given a finite undirected graph on n vertices, and the objective of the problem is to find a partition of the vertices of the graph into m sets that maximises the number of edges going between the two sets. So, MAX-CUT is the same as MAX-2-CUT.
$m>2$ candidates. Moreover, Theorem 1.1 fails to prove optimality of the Frieze-Jerrum [Reference Frieze and JerrumFJ95] semidefinite programming algorithm for the MAX-m-CUT problem. In the MAX-m-CUT problem, we are given a finite undirected graph on n vertices, and the objective of the problem is to find a partition of the vertices of the graph into m sets that maximises the number of edges going between the two sets. So, MAX-CUT is the same as MAX-2-CUT.
In order to prove the optimality of the Frieze-Jerrum [Reference Frieze and JerrumFJ95] semidefinite programming algorithm for the MAX-m-CUT problem, one would need an analogue of Theorem 1.1 for ![]() $m>2$ voters, where the plurality function replaces the majority function. For this reason, it was conjectured [Reference Khot, Kindler, Mossel and O’DonnellKKMO07, Reference Isaksson and MosselIM12] that the plurality function is the voting method that is most stable to independent, random vote corruption.
$m>2$ voters, where the plurality function replaces the majority function. For this reason, it was conjectured [Reference Khot, Kindler, Mossel and O’DonnellKKMO07, Reference Isaksson and MosselIM12] that the plurality function is the voting method that is most stable to independent, random vote corruption.
Conjecture 1.2 Plurality Is Stablest, Informal Version [Reference Khot, Kindler, Mossel and O’DonnellKKMO07], [Reference Isaksson and MosselIM12, Conjecture 1.9]
Suppose we run an election with a large number n of voters and ![]() $m\geq 3$ candidates. We make the following assumptions about voter behavior and about the election method.
$m\geq 3$ candidates. We make the following assumptions about voter behavior and about the election method.
• Voters cast their votes randomly, independently, with equal probability of voting for each candidate.
• Each voter has a small influence on the outcome of the election. (That is, all influences from Equation 5 are small for the voting method.)
• Each candidate has an equal chance of winning the election.
Under these assumptions, the plurality function is the voting method that best preserves the outcome of the election when votes have been corrupted independently each with probability less than ![]() $1/2$.
$1/2$.
We say that a vote ![]() $x_{i}\in \{1,\ldots ,m\}$ is corrupted with probability
$x_{i}\in \{1,\ldots ,m\}$ is corrupted with probability ![]() $0<\delta <1$ when, with probability
$0<\delta <1$ when, with probability ![]() $\delta $, the vote
$\delta $, the vote ![]() $x_{i}$ is changed to a uniformly random element of
$x_{i}$ is changed to a uniformly random element of ![]() $\{1,\ldots ,m\}$, and with probability
$\{1,\ldots ,m\}$, and with probability ![]() $1-\delta $, the vote
$1-\delta $, the vote ![]() $x_{i}$ is unchanged.
$x_{i}$ is unchanged.
In the case that the probability of vote corruption goes to zero, the first author proved the first known case of Conjecture 1.2 in [Reference HeilmanHei19], culminating in a series of previous works [Reference Colding and MinicozziCM12, Reference McGonagle and RossMR15, Reference Barchiesi, Brancolini and JulinBBJ17, Reference HeilmanHei17, Reference Milman and NeemanMN18a, Reference Milman and NeemanMN18b, Reference HeilmanHei18]. Conjecture 1.2 for all fixed parameters ![]() $0<\rho <1$ was entirely open until now. Unlike the case of the majority is stablest (Theorem 1.8), Conjecture 1.2 cannot hold when the candidates have unequal chances of winning the election [Reference Heilman, Mossel and NeemanHMN16]. This realization is an obstruction to proving Conjecture 1.2. It suggested that existing proof methods for Theorem 1.8 cannot apply to Conjecture 1.2.
$0<\rho <1$ was entirely open until now. Unlike the case of the majority is stablest (Theorem 1.8), Conjecture 1.2 cannot hold when the candidates have unequal chances of winning the election [Reference Heilman, Mossel and NeemanHMN16]. This realization is an obstruction to proving Conjecture 1.2. It suggested that existing proof methods for Theorem 1.8 cannot apply to Conjecture 1.2.
Nevertheless, we are able to overcome this obstruction in the present work.
Theorem 1.3 Main Result, Informal Version
There exists ![]() $\varepsilon>0$ such that Conjecture 1.2 holds for
$\varepsilon>0$ such that Conjecture 1.2 holds for ![]() $m=3$ candidates, for all
$m=3$ candidates, for all ![]() $n\geq 1$, when the probability of a single vote being corrupted is any number in the range
$n\geq 1$, when the probability of a single vote being corrupted is any number in the range ![]() $(1/2-\varepsilon ,1/2)$.
$(1/2-\varepsilon ,1/2)$.
Theorem 1.3 is the first proven case of the plurality is stablest conjecture (Conjecture 1.2).
1.2 More Formal Introduction
Using a generalization of the central limit theorem known as the invariance principle [Reference Mossel, O’Donnell and OleszkiewiczMOO10, Reference Isaksson and MosselIM12], there is an equivalence between the discrete problem of Conjecture 1.2 and a continuous problem known as the standard simplex conjecture [Reference Isaksson and MosselIM12]. For more details on this equivalence, see Section 7 of [Reference Isaksson and MosselIM12]. We begin by providing some background for the latter conjecture, stated in Conjecture 1.6.
For any ![]() $k\geq 1$, we define the Gaussian density as
$k\geq 1$, we define the Gaussian density as
 $$ \begin{align} \begin{aligned} \gamma_{k}(x)&\colon = (2\pi)^{-k/2}e^{-\left\|x\right\|^{2}/2},\qquad \langle x,y\rangle\colon=\sum_{i=1}^{n+1}x_{i}y_{i},\qquad \left\|x\right\|^{2}\colon=\langle x,x\rangle,\\ &\qquad\forall\,x=(x_{1},\ldots,x_{n+1}),y=(y_{1},\ldots,y_{n+1})\in\mathbb{R}^{n+1}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \gamma_{k}(x)&\colon = (2\pi)^{-k/2}e^{-\left\|x\right\|^{2}/2},\qquad \langle x,y\rangle\colon=\sum_{i=1}^{n+1}x_{i}y_{i},\qquad \left\|x\right\|^{2}\colon=\langle x,x\rangle,\\ &\qquad\forall\,x=(x_{1},\ldots,x_{n+1}),y=(y_{1},\ldots,y_{n+1})\in\mathbb{R}^{n+1}. \end{aligned} \end{align} $$ Let ![]() $z_{1},\ldots ,z_{m}\in \mathbb {R}^{n+1}$ be the vertices of a regular simplex in
$z_{1},\ldots ,z_{m}\in \mathbb {R}^{n+1}$ be the vertices of a regular simplex in ![]() $\mathbb {R}^{n+1}$ centred at the origin. For any
$\mathbb {R}^{n+1}$ centred at the origin. For any ![]() $1\leq i\leq m$, define
$1\leq i\leq m$, define
 $$ \begin{align} \Omega_{i}\colon=\{x\in\mathbb{R}^{n+1}\colon\langle x,z_{i}\rangle=\max_{1\leq j\leq m}\langle x,z_{j}\rangle\}. \end{align} $$
$$ \begin{align} \Omega_{i}\colon=\{x\in\mathbb{R}^{n+1}\colon\langle x,z_{i}\rangle=\max_{1\leq j\leq m}\langle x,z_{j}\rangle\}. \end{align} $$We refer to any sets satisfying (2) as cones over a regular simplex.
Let ![]() $f\colon \mathbb {R}^{n+1}\to [0,1]$ be measurable and let
$f\colon \mathbb {R}^{n+1}\to [0,1]$ be measurable and let ![]() $\rho \in (-1,1)$. Define the Ornstein–Uhlenbeck operator with correlation
$\rho \in (-1,1)$. Define the Ornstein–Uhlenbeck operator with correlation ![]() $\rho $ applied to f by
$\rho $ applied to f by
 $$ \begin{align} \begin{aligned} T_{\rho}f(x) \colon =\,&\int_{\mathbb{R}^{n+1}}f(x\rho+y\sqrt{1-\rho^{2}})\gamma_{n+1}(y)\,\mathrm{d} y\\ =\,&(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\int_{\mathbb{R}^{n+1}}f(y)e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y, \qquad\forall x\in\mathbb{R}^{n+1}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} T_{\rho}f(x) \colon =\,&\int_{\mathbb{R}^{n+1}}f(x\rho+y\sqrt{1-\rho^{2}})\gamma_{n+1}(y)\,\mathrm{d} y\\ =\,&(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\int_{\mathbb{R}^{n+1}}f(y)e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y, \qquad\forall x\in\mathbb{R}^{n+1}. \end{aligned} \end{align} $$![]() $T_{\rho }$ is a parametrization of the Ornstein–Uhlenbeck operator, which gives a fundamental solution of the (Gaussian) heat equation
$T_{\rho }$ is a parametrization of the Ornstein–Uhlenbeck operator, which gives a fundamental solution of the (Gaussian) heat equation
 $$ \begin{align} \frac{d}{d\rho}T_{\rho}f(x)=\frac{1}{\rho}\Big(-\overline{\Delta} T_{\rho}f(x)+\langle x,\overline{\nabla}T_{\rho}f(x)\rangle\Big),\qquad\forall\,x\in\mathbb{R}^{n+1}. \end{align} $$
$$ \begin{align} \frac{d}{d\rho}T_{\rho}f(x)=\frac{1}{\rho}\Big(-\overline{\Delta} T_{\rho}f(x)+\langle x,\overline{\nabla}T_{\rho}f(x)\rangle\Big),\qquad\forall\,x\in\mathbb{R}^{n+1}. \end{align} $$Here  $\overline {\Delta }\colon =\sum _{i=1}^{n+1}\partial ^{2}/\partial x_{i}^{2}$ and
$\overline {\Delta }\colon =\sum _{i=1}^{n+1}\partial ^{2}/\partial x_{i}^{2}$ and ![]() $\overline {\nabla }$ is the usual gradient on
$\overline {\nabla }$ is the usual gradient on ![]() $\mathbb {R}^{n+1}$.
$\mathbb {R}^{n+1}$. ![]() $T_{\rho }$ is not a semigroup, but it satisfies
$T_{\rho }$ is not a semigroup, but it satisfies ![]() $T_{\rho _{1}}T_{\rho _{2}}=T_{\rho _{1}\rho _{2}}$ for all
$T_{\rho _{1}}T_{\rho _{2}}=T_{\rho _{1}\rho _{2}}$ for all ![]() $\rho _{1},\rho _{2}\in (0,1)$. We have chosen this definition because the usual Ornstein–Uhlenbeck operator is only defined for
$\rho _{1},\rho _{2}\in (0,1)$. We have chosen this definition because the usual Ornstein–Uhlenbeck operator is only defined for ![]() $\rho \in [0,1]$.
$\rho \in [0,1]$.
Definition 1.4 Noise Stability
Let ![]() $\Omega \subseteq \mathbb {R}^{n+1}$ be measurable. Let
$\Omega \subseteq \mathbb {R}^{n+1}$ be measurable. Let ![]() $\rho \in (-1,1)$. We define the noise stability of the set
$\rho \in (-1,1)$. We define the noise stability of the set ![]() $\Omega $ with correlation
$\Omega $ with correlation ![]() $\rho $ to be
$\rho $ to be
 $$ \begin{align*} \int_{\mathbb{R}^{n+1}}1_{\Omega}(x)T_{\rho}1_{\Omega}(x)\gamma_{n+1}(x)\,\mathrm{d} x \stackrel{(3)}{=}(2\pi)^{-(n+1)}(1-\rho^{2})^{-(n+1)/2}\int_{\Omega}\int_{\Omega}e^{\frac{-\|x\|^{2}-\|y\|^{2}+2\rho\langle x,y\rangle}{2(1-\rho^{2})}}\,\mathrm{d} x\mathrm{d} y. \end{align*} $$
$$ \begin{align*} \int_{\mathbb{R}^{n+1}}1_{\Omega}(x)T_{\rho}1_{\Omega}(x)\gamma_{n+1}(x)\,\mathrm{d} x \stackrel{(3)}{=}(2\pi)^{-(n+1)}(1-\rho^{2})^{-(n+1)/2}\int_{\Omega}\int_{\Omega}e^{\frac{-\|x\|^{2}-\|y\|^{2}+2\rho\langle x,y\rangle}{2(1-\rho^{2})}}\,\mathrm{d} x\mathrm{d} y. \end{align*} $$Equivalently, if ![]() $X=(X_{1},\ldots ,X_{n+1}),Y=(Y_{1},\ldots ,Y_{n+1})\in \mathbb {R}^{n+1}$ are
$X=(X_{1},\ldots ,X_{n+1}),Y=(Y_{1},\ldots ,Y_{n+1})\in \mathbb {R}^{n+1}$ are ![]() $(n+1)$-dimensional jointly Gaussian distributed random vectors with
$(n+1)$-dimensional jointly Gaussian distributed random vectors with ![]() $\mathbb {E} X_{i}Y_{j}=\rho \cdot 1_{(i=j)}$ for all
$\mathbb {E} X_{i}Y_{j}=\rho \cdot 1_{(i=j)}$ for all ![]() $i,j\in \{1,\ldots ,n+1\}$, then
$i,j\in \{1,\ldots ,n+1\}$, then
 $$ \begin{align*} \int_{\mathbb{R}^{n+1}}1_{\Omega}(x)T_{\rho}1_{\Omega}(x)\gamma_{n+1}(x)\,\mathrm{d} x=\mathbb{P}((X,Y)\in \Omega\times \Omega). \end{align*} $$
$$ \begin{align*} \int_{\mathbb{R}^{n+1}}1_{\Omega}(x)T_{\rho}1_{\Omega}(x)\gamma_{n+1}(x)\,\mathrm{d} x=\mathbb{P}((X,Y)\in \Omega\times \Omega). \end{align*} $$Maximising the noise stability of a Euclidean partition is the continuous analogue of finding a voting method that is most stable to random corruption of votes among voting methods where each voter has a small influence on the election’s outcome.
Problem 1.5 Standard Simplex Problem [Reference Isaksson and MosselIM12]
Let ![]() $m\geq 3$. Fix
$m\geq 3$. Fix ![]() $a_{1},\ldots ,a_{m}>0$ such that
$a_{1},\ldots ,a_{m}>0$ such that ![]() $\sum _{i=1}^{m}a_{i}=1$. Fix
$\sum _{i=1}^{m}a_{i}=1$. Fix ![]() $\rho \in (0,1)$. Find measurable sets
$\rho \in (0,1)$. Find measurable sets ![]() $\Omega _{1},\ldots \Omega _{m}\subseteq \mathbb {R}^{n+1}$ with
$\Omega _{1},\ldots \Omega _{m}\subseteq \mathbb {R}^{n+1}$ with  $\cup _{i=1}^{m}\Omega _{i}=\mathbb {R}^{n+1}$ and
$\cup _{i=1}^{m}\Omega _{i}=\mathbb {R}^{n+1}$ and ![]() $\gamma _{n+1}(\Omega _{i})=a_{i}$ for all
$\gamma _{n+1}(\Omega _{i})=a_{i}$ for all ![]() $1\leq i\leq m$ that maximise
$1\leq i\leq m$ that maximise
 $$ \begin{align*} \sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}}1_{\Omega_{i}}(x)T_{\rho}1_{\Omega_{i}}(x)\gamma_{n+1}(x)\,\mathrm{d} x, \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}}1_{\Omega_{i}}(x)T_{\rho}1_{\Omega_{i}}(x)\gamma_{n+1}(x)\,\mathrm{d} x, \end{align*} $$subject to the above constraints. (Here  $\gamma _{n+1}(\Omega _{i})\colon =\int _{\Omega _{i}}\gamma _{n+1}(x)\,\mathrm {d} x \ \forall \ 1\leq i\leq m$.)
$\gamma _{n+1}(\Omega _{i})\colon =\int _{\Omega _{i}}\gamma _{n+1}(x)\,\mathrm {d} x \ \forall \ 1\leq i\leq m$.)
We can now state the continuous version of Conjecture 1.2.
Conjecture 1.6 Standard Simplex Conjecture [Reference Isaksson and MosselIM12]
Let ![]() $\Omega _{1},\ldots \Omega _{m}\subseteq \mathbb {R}^{n+1}$ maximise Problem 1.5. Assume that
$\Omega _{1},\ldots \Omega _{m}\subseteq \mathbb {R}^{n+1}$ maximise Problem 1.5. Assume that ![]() $m-1\leq n+1$. Fix
$m-1\leq n+1$. Fix ![]() $\rho \in (0,1)$. Let
$\rho \in (0,1)$. Let ![]() $z_{1},\ldots ,z_{m}\in \mathbb {R}^{n+1}$ be the vertices of a regular simplex in
$z_{1},\ldots ,z_{m}\in \mathbb {R}^{n+1}$ be the vertices of a regular simplex in ![]() $\mathbb {R}^{n+1}$ centred at the origin. Then
$\mathbb {R}^{n+1}$ centred at the origin. Then ![]() $\exists \ w\in \mathbb {R}^{n+1}$ such that, for all
$\exists \ w\in \mathbb {R}^{n+1}$ such that, for all ![]() $1\leq i\leq m$,
$1\leq i\leq m$,
 $$ \begin{align*}\Omega_{i}=w+\{x\in\mathbb{R}^{n+1}\colon\langle x,z_{i}\rangle=\max_{1\leq j\leq m}\langle x,z_{j}\rangle\}.\end{align*} $$
$$ \begin{align*}\Omega_{i}=w+\{x\in\mathbb{R}^{n+1}\colon\langle x,z_{i}\rangle=\max_{1\leq j\leq m}\langle x,z_{j}\rangle\}.\end{align*} $$ It is known that Conjecture 1.6 is false when ![]() $(a_{1},\ldots ,a_{m})\neq (1/m,\ldots ,1/m)$ [Reference Heilman, Mossel and NeemanHMN16]. In the remaining case that
$(a_{1},\ldots ,a_{m})\neq (1/m,\ldots ,1/m)$ [Reference Heilman, Mossel and NeemanHMN16]. In the remaining case that ![]() $a_{i}=1/m$ for all
$a_{i}=1/m$ for all ![]() $1\leq i\leq m$, it is assumed that
$1\leq i\leq m$, it is assumed that ![]() $w=0$ in Conjecture 1.6.
$w=0$ in Conjecture 1.6.
For expositional simplicity, we separately address the case ![]() $\rho <0$ of Conjecture 1.6 in Section 7.
$\rho <0$ of Conjecture 1.6 in Section 7.
1.3 Plurality Is Stablest Conjecture
As previously mentioned, the standard simplex conjecture [Reference Isaksson and MosselIM12] stated in Conjecture 1.6 is essentially equivalent to the plurality is stablest conjecture from Conjecture 1.2. After making several definitions, we state a formal version of Conjecture 1.2 as Conjecture 1.7.
If ![]() $g\colon \{1,\ldots ,m\}^{n}\to \mathbb {R}$ and
$g\colon \{1,\ldots ,m\}^{n}\to \mathbb {R}$ and ![]() $1\leq i\leq n$, we denote
$1\leq i\leq n$, we denote
 $$ \begin{align*}\mathbb{E}(g)\colon= m^{-n}\sum_{\omega\in\{1,\ldots,m\}^{n}} g(\omega)\end{align*} $$
$$ \begin{align*}\mathbb{E}(g)\colon= m^{-n}\sum_{\omega\in\{1,\ldots,m\}^{n}} g(\omega)\end{align*} $$ $$ \begin{align*}\mathbb{E}_{i}(g)(\omega_{1},\ldots,\omega_{i-1},\omega_{i+1},\ldots,\omega_{n})\colon= m^{-1}\sum_{\omega_{i}\in\{1,\ldots,m\}} g(\omega_{1},\ldots,\omega_{n})\end{align*} $$
$$ \begin{align*}\mathbb{E}_{i}(g)(\omega_{1},\ldots,\omega_{i-1},\omega_{i+1},\ldots,\omega_{n})\colon= m^{-1}\sum_{\omega_{i}\in\{1,\ldots,m\}} g(\omega_{1},\ldots,\omega_{n})\end{align*} $$Define also the ith influence of g – that is, the influence of the ![]() $i^{th}$ voter of g – as
$i^{th}$ voter of g – as
Let
If ![]() $f\colon \{1,\ldots ,m\}^{n}\to \Delta _{m}$, we denote the coordinates of f as
$f\colon \{1,\ldots ,m\}^{n}\to \Delta _{m}$, we denote the coordinates of f as ![]() $f=(f_{1},\ldots ,f_{m})$. For any
$f=(f_{1},\ldots ,f_{m})$. For any ![]() $\omega \in \mathbb {Z}^{n}$, we denote
$\omega \in \mathbb {Z}^{n}$, we denote ![]() $\left \|\omega \right \|_{0}$ as the number of nonzero coordinates of
$\left \|\omega \right \|_{0}$ as the number of nonzero coordinates of ![]() $\omega $. The noise stability of
$\omega $. The noise stability of ![]() $g\colon \{1,\ldots ,m\}^{n}\to \mathbb {R}$ with parameter
$g\colon \{1,\ldots ,m\}^{n}\to \mathbb {R}$ with parameter ![]() $\rho \in (-1,1)$ is
$\rho \in (-1,1)$ is
 $$ \begin{align*} S_{\rho} g \colon =\,& m^{-n}\sum_{\omega\in\{1,\ldots,m\}^{n}} g(\omega)\mathbb{E}_{\rho} g(\delta)\\ =\,& m^{-n}\sum_{\omega\in\{1,\ldots,m\}^{n}} g(\omega)\sum_{\sigma\in\{1,\ldots,m\}^{n}}\left(\frac{1-(m-1)\rho}{m}\right)^{n-\left\|\sigma-\omega\right\|_{0}} \left(\frac{1-\rho}{m}\right)^{\left\|\sigma-\omega\right\|_{0}} g(\sigma). \end{align*} $$
$$ \begin{align*} S_{\rho} g \colon =\,& m^{-n}\sum_{\omega\in\{1,\ldots,m\}^{n}} g(\omega)\mathbb{E}_{\rho} g(\delta)\\ =\,& m^{-n}\sum_{\omega\in\{1,\ldots,m\}^{n}} g(\omega)\sum_{\sigma\in\{1,\ldots,m\}^{n}}\left(\frac{1-(m-1)\rho}{m}\right)^{n-\left\|\sigma-\omega\right\|_{0}} \left(\frac{1-\rho}{m}\right)^{\left\|\sigma-\omega\right\|_{0}} g(\sigma). \end{align*} $$Equivalently, conditional on ![]() $\omega $,
$\omega $, ![]() $\mathbb {E}_{\rho }g(\delta )$ is defined so that for all
$\mathbb {E}_{\rho }g(\delta )$ is defined so that for all ![]() $1\leq i\leq n$,
$1\leq i\leq n$, ![]() $\delta _{i}=\omega _{i}$ with probability
$\delta _{i}=\omega _{i}$ with probability  $\frac {1-(m-1)\rho }{m}$, and
$\frac {1-(m-1)\rho }{m}$, and ![]() $\delta _{i}$ is equal to any of the other
$\delta _{i}$ is equal to any of the other ![]() $(m-1)$ elements of
$(m-1)$ elements of ![]() $\{1,\ldots ,m\}$ each with probability
$\{1,\ldots ,m\}$ each with probability  $\frac {1-\rho }{m}$, so that
$\frac {1-\rho }{m}$, so that ![]() $\delta _{1},\ldots ,\delta _{n}$ are independent.
$\delta _{1},\ldots ,\delta _{n}$ are independent.
The noise stability of ![]() $f\colon \{1,\ldots ,m\}^{n}\to \Delta _{m}$ with parameter
$f\colon \{1,\ldots ,m\}^{n}\to \Delta _{m}$ with parameter ![]() $\rho \in (-1,1)$ is
$\rho \in (-1,1)$ is
 $$ \begin{align*}S_{\rho}f\colon=\sum_{i=1}^{m}S_{\rho}f_{i}.\end{align*} $$
$$ \begin{align*}S_{\rho}f\colon=\sum_{i=1}^{m}S_{\rho}f_{i}.\end{align*} $$ Let ![]() $m\geq 2$,
$m\geq 2$, ![]() $k\geq 3$. For each
$k\geq 3$. For each ![]() $j\in \{1,\ldots ,m\}$, let
$j\in \{1,\ldots ,m\}$, let ![]() $e_{j}=(0,\ldots ,0,1,0,\ldots ,0)\in \mathbb {R}^{m}$ be the jth unit coordinate vector. Define the plurality function
$e_{j}=(0,\ldots ,0,1,0,\ldots ,0)\in \mathbb {R}^{m}$ be the jth unit coordinate vector. Define the plurality function ![]() $\mathrm {PLUR}_{m,n}\colon \{1,\ldots ,m\}^{n}\to \Delta _{m}$ for m candidates and n voters such that for all
$\mathrm {PLUR}_{m,n}\colon \{1,\ldots ,m\}^{n}\to \Delta _{m}$ for m candidates and n voters such that for all ![]() $\omega \in \{1,\ldots ,m\}^{n}$.
$\omega \in \{1,\ldots ,m\}^{n}$.
 $$ \begin{align*}\mathrm{PLUR}_{m,n}(\omega) \colon=\begin{cases} e_{j}&,\mbox{if }\left|\{i\in\{1,\ldots,m\}\colon\omega_{i}=j\}\right|>\left|\{i\in\{1,\ldots,m\}\colon\omega_{i}=r\}\right|,\\ &\qquad\qquad\qquad\qquad\forall\,r\in\{1,\ldots,m\}\setminus\{j\}\\ \frac{1}{m}\sum_{i=1}^{m}e_{i}&,\mbox{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*}\mathrm{PLUR}_{m,n}(\omega) \colon=\begin{cases} e_{j}&,\mbox{if }\left|\{i\in\{1,\ldots,m\}\colon\omega_{i}=j\}\right|>\left|\{i\in\{1,\ldots,m\}\colon\omega_{i}=r\}\right|,\\ &\qquad\qquad\qquad\qquad\forall\,r\in\{1,\ldots,m\}\setminus\{j\}\\ \frac{1}{m}\sum_{i=1}^{m}e_{i}&,\mbox{otherwise}. \end{cases} \end{align*} $$We can now state the more formal version of Conjecture 1.2.
Conjecture 1.7 Plurality Is Stablest, Discrete Version
For any ![]() $m\geq 2$,
$m\geq 2$, ![]() $\rho \in [0,1]$,
$\rho \in [0,1]$, ![]() $\varepsilon>0$, there exists
$\varepsilon>0$, there exists ![]() $\tau>0$ such that if
$\tau>0$ such that if ![]() $f\colon \{1,\ldots ,m\}^{n}\to \Delta _{m}$ satisfies
$f\colon \{1,\ldots ,m\}^{n}\to \Delta _{m}$ satisfies ![]() $\mathrm {Inf}_{i}(f_{j})\leq \tau $ for all
$\mathrm {Inf}_{i}(f_{j})\leq \tau $ for all ![]() $1\leq i\leq n$ and for all
$1\leq i\leq n$ and for all ![]() $1\leq j\leq m$, and if
$1\leq j\leq m$, and if  $\mathbb {E} f=\frac {1}{m}\sum _{i=1}^{m}e_{i}$, then
$\mathbb {E} f=\frac {1}{m}\sum _{i=1}^{m}e_{i}$, then
 $$ \begin{align*}S_{\rho}f\leq \lim_{n\to\infty}S_{\rho}\mathrm{PLUR}_{m,n}+\varepsilon. \end{align*} $$
$$ \begin{align*}S_{\rho}f\leq \lim_{n\to\infty}S_{\rho}\mathrm{PLUR}_{m,n}+\varepsilon. \end{align*} $$ The main result of the present article (stated in Theorem 1.10) is ![]() $\exists \ \rho _{0}>0$ such that Conjecture 1.7 is true for
$\exists \ \rho _{0}>0$ such that Conjecture 1.7 is true for ![]() $m=3$ for all
$m=3$ for all ![]() $0<\rho <\rho _{0}$, for all
$0<\rho <\rho _{0}$, for all ![]() $n\geq 1$. The only previously known case of Conjecture 1.7 was the following.
$n\geq 1$. The only previously known case of Conjecture 1.7 was the following.
Theorem 1.8 Majority Is Stablest, Formal, Biased Case [Reference Mossel, O’Donnell and OleszkiewiczMOO10, Theorem 4.4]
Conjecture 1.7 is true when ![]() $m=2$.
$m=2$.
For an even more general version of Theorem 1.8, see [Reference Mossel, O’Donnell and OleszkiewiczMOO10, Theorem 4.4]. In particular, the assumption on ![]() $\mathbb {E} f$ can be removed, though we know that this cannot be done for
$\mathbb {E} f$ can be removed, though we know that this cannot be done for ![]() $m\geq 3$ [Reference Heilman, Mossel and NeemanHMN16].
$m\geq 3$ [Reference Heilman, Mossel and NeemanHMN16].
1.4 Our Contribution
The main structure theorem below implies that sets optimising noise stability in Problem 1.5 are inherently low-dimensional. Though this statement might seem intuitively true, because many inequalities involving the Gaussian measure have low-dimensional optimisers, this statement has not been proven before. For example, Theorem 1.9 was listed as an open question in [Reference De, Mossel and NeemanDMN17, Reference De, Mossel and NeemanDMN18] and [Reference Ghazi, Kamath and RaghavendraGKR18]. Indeed, the lack of Theorem 1.9 has been one main obstruction to a solution of Conjectures 1.5 and 1.7.
Theorem 1.9 Main Structure Theorem/Dimension Reduction
Fix ![]() $\rho \in (0,1)$. Let
$\rho \in (0,1)$. Let ![]() $m\geq 2$ with
$m\geq 2$ with ![]() $m\leq n+2$. Let
$m\leq n+2$. Let ![]() $\Omega _{1},\ldots \Omega _{m}\subseteq \mathbb {R}^{n+1}$ maximise Problem 1.5. Then, after rotating the sets
$\Omega _{1},\ldots \Omega _{m}\subseteq \mathbb {R}^{n+1}$ maximise Problem 1.5. Then, after rotating the sets ![]() $\Omega _{1},\ldots \Omega _{m}$ and applying Lebesgue measure zero changes to these sets, there exist measurable sets
$\Omega _{1},\ldots \Omega _{m}$ and applying Lebesgue measure zero changes to these sets, there exist measurable sets  $\Omega _{1}',\ldots \Omega _{m}'\subseteq \mathbb {R}^{m-1}$ such that
$\Omega _{1}',\ldots \Omega _{m}'\subseteq \mathbb {R}^{m-1}$ such that
 $$ \begin{align*}\Omega_{i}=\Omega_{i}'\times\mathbb{R}^{n-m+2},\qquad\forall\, 1\leq i\leq m.\end{align*} $$
$$ \begin{align*}\Omega_{i}=\Omega_{i}'\times\mathbb{R}^{n-m+2},\qquad\forall\, 1\leq i\leq m.\end{align*} $$ In the case ![]() $m=2$, Theorem 1.9 is (almost) a variational proof of Borell’s inequality, because it reduces Problem 1.5 to a 1-dimensional problem.
$m=2$, Theorem 1.9 is (almost) a variational proof of Borell’s inequality, because it reduces Problem 1.5 to a 1-dimensional problem.
In the case ![]() $m=3$, Theorem 1.9 says that Conjecture 1.6 for arbitrary
$m=3$, Theorem 1.9 says that Conjecture 1.6 for arbitrary ![]() $n+1$ reduces to the case
$n+1$ reduces to the case ![]() $n+1=2$, which was solved for small
$n+1=2$, which was solved for small ![]() $\rho>0$ in [Reference HeilmanHei14]. That is, Theorem 1.9 and the main result of [Reference HeilmanHei14] imply the following.
$\rho>0$ in [Reference HeilmanHei14]. That is, Theorem 1.9 and the main result of [Reference HeilmanHei14] imply the following.
Theorem 1.10 Main; Plurality Is Stablest for Three Candidates and Small Correlation
There exists ![]() $\rho _{0}>0$ such that Conjecture 1.7 is true for
$\rho _{0}>0$ such that Conjecture 1.7 is true for ![]() $m=3$ and for all
$m=3$ and for all ![]() $0<\rho <\rho _{0}$.
$0<\rho <\rho _{0}$.
In [Reference HeilmanHei14] it is noted that  $\rho _{0}=e^{-20\cdot 3^{10^{14}}}$ suffices in Theorem 1.10.
$\rho _{0}=e^{-20\cdot 3^{10^{14}}}$ suffices in Theorem 1.10.
We can also prove a version of Theorem 1.9 when ![]() $\rho <0$. See Theorem 7.9 and the discussion in Section 7. One difficulty in proving Theorem 1.9 directly for
$\rho <0$. See Theorem 7.9 and the discussion in Section 7. One difficulty in proving Theorem 1.9 directly for ![]() $\rho <0$ is that it is not a priori obvious that a minimiser of Problem 1.5 exists in that case.
$\rho <0$ is that it is not a priori obvious that a minimiser of Problem 1.5 exists in that case.
1.5 Noninteractive Simulation of Correlated Distributions
As mentioned above, Theorem 1.9 answers a question in [Reference De, Mossel and NeemanDMN17, Reference De, Mossel and NeemanDMN18] and [Reference Ghazi, Kamath and RaghavendraGKR18]. Their interest in Theorem 1.9 stems from the following problem. Let ![]() $(X,Y)\in \mathbb {R}^{n}$ be a random vector. Let
$(X,Y)\in \mathbb {R}^{n}$ be a random vector. Let ![]() $(X_{1},Y_{1}),(X_{2},Y_{2}),\ldots $ be independent and identically distributed copies of
$(X_{1},Y_{1}),(X_{2},Y_{2}),\ldots $ be independent and identically distributed copies of ![]() $(X,Y)$. Suppose there are two players A and B. Player A has access to
$(X,Y)$. Suppose there are two players A and B. Player A has access to ![]() $X_{1},X_{2},\ldots $ and player B has access to
$X_{1},X_{2},\ldots $ and player B has access to ![]() $Y_{1},Y_{2},\ldots $. Without communication, what joint distributions can players A and B jointly simulate? For details on the relation of this problem to Theorem 1.9, see [Reference De, Mossel and NeemanDMN17, Reference De, Mossel and NeemanDMN18] and [Reference Ghazi, Kamath and RaghavendraGKR18].
$Y_{1},Y_{2},\ldots $. Without communication, what joint distributions can players A and B jointly simulate? For details on the relation of this problem to Theorem 1.9, see [Reference De, Mossel and NeemanDMN17, Reference De, Mossel and NeemanDMN18] and [Reference Ghazi, Kamath and RaghavendraGKR18].
1.6 Outline of the Proof of the Structure Theorem
In this section we outline the proof of Theorem 1.9 in the case ![]() $m=2$. The proof loosely follows that of a corresponding statement [Reference McGonagle and RossMR15, Reference Barchiesi, Brancolini and JulinBBJ17] for the Gaussian surface area (which was then adapted to multiple sets in [Reference Milman and NeemanMN18a, Reference Milman and NeemanMN18b, Reference HeilmanHei18]), with a few key differences. For didactic purposes, we will postpone a discussion of technical difficulties (such as existence and regularity of a maximiser) to Subsection 2.1.
$m=2$. The proof loosely follows that of a corresponding statement [Reference McGonagle and RossMR15, Reference Barchiesi, Brancolini and JulinBBJ17] for the Gaussian surface area (which was then adapted to multiple sets in [Reference Milman and NeemanMN18a, Reference Milman and NeemanMN18b, Reference HeilmanHei18]), with a few key differences. For didactic purposes, we will postpone a discussion of technical difficulties (such as existence and regularity of a maximiser) to Subsection 2.1.
Fix ![]() $0<a<1$. Suppose there exists
$0<a<1$. Suppose there exists ![]() $\Omega ,\Omega ^{c}\subseteq \mathbb {R}^{n+1}$ are measurable sets maximizing
$\Omega ,\Omega ^{c}\subseteq \mathbb {R}^{n+1}$ are measurable sets maximizing
 $$ \begin{align*}\int_{\mathbb{R}^{n+1}}1_{\Omega}(x)T_{\rho}1_{\Omega}(x)\gamma_{n+1}(x)dx,\end{align*} $$
$$ \begin{align*}\int_{\mathbb{R}^{n+1}}1_{\Omega}(x)T_{\rho}1_{\Omega}(x)\gamma_{n+1}(x)dx,\end{align*} $$subject to the constraint ![]() $\gamma _{n+1}(\Omega )=a$. A first variation argument (Lemma 3.1) implies that
$\gamma _{n+1}(\Omega )=a$. A first variation argument (Lemma 3.1) implies that ![]() $\Sigma \colon =\partial \Omega $ is a level set of the Ornstein–Uhlenbeck operator applied to
$\Sigma \colon =\partial \Omega $ is a level set of the Ornstein–Uhlenbeck operator applied to ![]() $1_{\Omega }$. That is, there exists
$1_{\Omega }$. That is, there exists ![]() $c\in \mathbb {R}$ such that
$c\in \mathbb {R}$ such that
 $$ \begin{align} \Sigma=\{x\in\mathbb{R}^{n+1}\colon T_{\rho}1_{\Omega}(x)=c\}. \end{align} $$
$$ \begin{align} \Sigma=\{x\in\mathbb{R}^{n+1}\colon T_{\rho}1_{\Omega}(x)=c\}. \end{align} $$Because ![]() $\Sigma $ is a level set, a vector perpendicular to the level set is also perpendicular to
$\Sigma $ is a level set, a vector perpendicular to the level set is also perpendicular to ![]() $\Sigma $. Denoting
$\Sigma $. Denoting ![]() $N(x)\in \mathbb {R}^{n+1}$ as the unit length exterior pointing normal vector to
$N(x)\in \mathbb {R}^{n+1}$ as the unit length exterior pointing normal vector to ![]() $x\in \partial \Omega $, (7) implies that
$x\in \partial \Omega $, (7) implies that
 $$ \begin{align} \overline{\nabla}T_{\rho}1_{\Omega}(x)= -N(x)\|\overline{\nabla}T_{\rho}1_{\Omega}(x)\|. \end{align} $$
$$ \begin{align} \overline{\nabla}T_{\rho}1_{\Omega}(x)= -N(x)\|\overline{\nabla}T_{\rho}1_{\Omega}(x)\|. \end{align} $$(It is not obvious that there must be a negative sign here, but it follows from examining the second variation.) We now observe how the noise stability of ![]() $\Omega $ changes as the set is translated infinitesimally. Fix
$\Omega $ changes as the set is translated infinitesimally. Fix ![]() $v\in \mathbb {R}^{n+1}$ and consider the variation of
$v\in \mathbb {R}^{n+1}$ and consider the variation of ![]() $\Omega $ induced by the constant vector field v. That is, let
$\Omega $ induced by the constant vector field v. That is, let ![]() $\Psi \colon \mathbb {R}^{n+1}\times (-1,1)\to \mathbb {R}^{n+1}$ such that
$\Psi \colon \mathbb {R}^{n+1}\times (-1,1)\to \mathbb {R}^{n+1}$ such that ![]() $\Psi (x,0)=x$ and such that
$\Psi (x,0)=x$ and such that  $\frac {\mathrm {d}}{\mathrm {d} s}|_{s=0}\Psi (x,s)=v$ for all
$\frac {\mathrm {d}}{\mathrm {d} s}|_{s=0}\Psi (x,s)=v$ for all ![]() $x\in \mathbb {R}^{n+1},s\in (-1,1)$. For any
$x\in \mathbb {R}^{n+1},s\in (-1,1)$. For any ![]() $s\in (-1,1)$, let
$s\in (-1,1)$, let ![]() $\Omega ^{(s)}=\Psi (\Omega ,s)$. Note that
$\Omega ^{(s)}=\Psi (\Omega ,s)$. Note that ![]() $\Omega ^{(0)}=\Omega $. Denote
$\Omega ^{(0)}=\Omega $. Denote ![]() $f(x)\colon = \langle v,N(x)\rangle $ for all
$f(x)\colon = \langle v,N(x)\rangle $ for all ![]() $x\in \Sigma $. Then define
$x\in \Sigma $. Then define
 $$ \begin{align*}S(f)(x)\colon= (1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\int_{\Sigma}f(y)e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y,\qquad\forall\,x\in\Sigma. \end{align*} $$
$$ \begin{align*}S(f)(x)\colon= (1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\int_{\Sigma}f(y)e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y,\qquad\forall\,x\in\Sigma. \end{align*} $$A second variation argument (Lemma 4.5) implies that, if f is Gaussian volume preserving – that is,  $\int _{\Sigma }f(x)\gamma _{n+1}(x)\,\mathrm {d} x=0$ – then
$\int _{\Sigma }f(x)\gamma _{n+1}(x)\,\mathrm {d} x=0$ – then
 $$ \begin{align} \begin{aligned} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\int_{\mathbb{R}^{n+1}}1_{\Omega^{(s)}}(x)T_{\rho}1_{\Omega^{(s)}}(x)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad\qquad\qquad=\int_{\Sigma}\Big(S(f)(x)-\|\overline{\nabla}T_{\rho}1_{\Omega}(x)\|f(x)\Big)f(x)\gamma_{n+1}(x)\,\mathrm{d} x. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\int_{\mathbb{R}^{n+1}}1_{\Omega^{(s)}}(x)T_{\rho}1_{\Omega^{(s)}}(x)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad\qquad\qquad=\int_{\Sigma}\Big(S(f)(x)-\|\overline{\nabla}T_{\rho}1_{\Omega}(x)\|f(x)\Big)f(x)\gamma_{n+1}(x)\,\mathrm{d} x. \end{aligned} \end{align} $$Somewhat unexpected, the function ![]() $f(x)=\langle v,N(x)\rangle $ is almost an eigenfunction of the operator S (by Lemma 5.1), in the sense that
$f(x)=\langle v,N(x)\rangle $ is almost an eigenfunction of the operator S (by Lemma 5.1), in the sense that
 $$ \begin{align} S(f)(x)=\frac{1}{\rho}f(x)\|\overline{\nabla} T_{\rho}1_{\Omega}(x)\|,\qquad\forall\,x\in\Sigma. \end{align} $$
$$ \begin{align} S(f)(x)=\frac{1}{\rho}f(x)\|\overline{\nabla} T_{\rho}1_{\Omega}(x)\|,\qquad\forall\,x\in\Sigma. \end{align} $$Equation (10) is the key fact used in the proof of the main theorem, Theorem 1.9. Equation (10) follows from (8) and the divergence theorem (see Lemma 5.1 for a proof of (10).) Plugging (10) into (9),
 $$ \begin{align} \begin{aligned} \int_{\Sigma}\langle v,N(x)\rangle\gamma_{n+1}(x)\,\mathrm{d} x=0\quad\Longrightarrow\quad &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\int_{\mathbb{R}^{n+1}}1_{\Omega^{(s)}}(x)T_{\rho}1_{\Omega^{(s)}}(x)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad=\Big(\frac{1}{\rho}-1\Big)\int_{\Sigma}\langle v,N(x)\rangle^{2}\left\|\overline{\nabla}T_{\rho}1_{\Omega}(x)\right\|\gamma_{n+1}(x)\,\mathrm{d} x. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \int_{\Sigma}\langle v,N(x)\rangle\gamma_{n+1}(x)\,\mathrm{d} x=0\quad\Longrightarrow\quad &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\int_{\mathbb{R}^{n+1}}1_{\Omega^{(s)}}(x)T_{\rho}1_{\Omega^{(s)}}(x)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad=\Big(\frac{1}{\rho}-1\Big)\int_{\Sigma}\langle v,N(x)\rangle^{2}\left\|\overline{\nabla}T_{\rho}1_{\Omega}(x)\right\|\gamma_{n+1}(x)\,\mathrm{d} x. \end{aligned} \end{align} $$The set
 $$ \begin{align*} V\colon=\Big\{v\in\mathbb{R}^{n+1}\colon \int_{\Sigma}\langle v,N(x)\rangle\gamma_{n+1}(x)\,\mathrm{d} x=0\Big\} \end{align*} $$
$$ \begin{align*} V\colon=\Big\{v\in\mathbb{R}^{n+1}\colon \int_{\Sigma}\langle v,N(x)\rangle\gamma_{n+1}(x)\,\mathrm{d} x=0\Big\} \end{align*} $$has dimension at least n, by the rank-nullity theorem. Because ![]() $\Omega $ maximises noise stability, the quantity on the right of (11) must be nonpositive for all
$\Omega $ maximises noise stability, the quantity on the right of (11) must be nonpositive for all ![]() $v\in V$, implying that
$v\in V$, implying that ![]() $f=0$ on
$f=0$ on ![]() $\Sigma $ (except possibly on a set of measure zero on
$\Sigma $ (except possibly on a set of measure zero on ![]() $\Sigma $. One can show that
$\Sigma $. One can show that  $\left \|\overline {\nabla }T_{\rho }1_{\Omega }(x)\right \|>0$ for all
$\left \|\overline {\nabla }T_{\rho }1_{\Omega }(x)\right \|>0$ for all ![]() $x\in \Sigma $. See Lemma 4.8.) That is, for all
$x\in \Sigma $. See Lemma 4.8.) That is, for all ![]() $v\in V$,
$v\in V$, ![]() $\langle v,N(x)\rangle =0$ for all
$\langle v,N(x)\rangle =0$ for all ![]() $x\in \Sigma $ (except possibly on a set of measure zero on
$x\in \Sigma $ (except possibly on a set of measure zero on ![]() $\Sigma $). Because V has dimension at least n, there exists a measurable discrete set
$\Sigma $). Because V has dimension at least n, there exists a measurable discrete set ![]() $\Omega '\subseteq \mathbb {R}$ such that
$\Omega '\subseteq \mathbb {R}$ such that ![]() $\Omega =\Omega '\times \mathbb {R}^{n}$ after rotating
$\Omega =\Omega '\times \mathbb {R}^{n}$ after rotating ![]() $\Omega $, concluding the proof of Theorem 1.9 in the case
$\Omega $, concluding the proof of Theorem 1.9 in the case ![]() $m=2$.
$m=2$.
Theorem 1.9 follows from the realization that all of the above steps still hold for arbitrary m in Conjecture 1.5. In particular, the key lemma (10) still holds. See Lemmas 5.1 and 5.4.
Remark 1.11. In the case that we replace the Gaussian noise stability of ![]() $\Omega $ with the Euclidean heat content
$\Omega $ with the Euclidean heat content
 $$ \begin{align*}\int_{\mathbb{R}^{n+1}}1_{\Omega}(x)P_{t}1_{\Omega}(x)\,\mathrm{d} x,\qquad\forall\,t>0 \end{align*} $$
$$ \begin{align*}\int_{\mathbb{R}^{n+1}}1_{\Omega}(x)P_{t}1_{\Omega}(x)\,\mathrm{d} x,\qquad\forall\,t>0 \end{align*} $$ $$ \begin{align*}P_{t}f(x) \colon=\int_{\mathbb{R}^{n+1}}f(x+y\sqrt{t})\gamma_{n+1}(y)\,\mathrm{d} y, \qquad\forall x\in\mathbb{R}^{n+1},\qquad\forall\,f\colon\mathbb{R}^{n+1}\to[0,1],\end{align*} $$
$$ \begin{align*}P_{t}f(x) \colon=\int_{\mathbb{R}^{n+1}}f(x+y\sqrt{t})\gamma_{n+1}(y)\,\mathrm{d} y, \qquad\forall x\in\mathbb{R}^{n+1},\qquad\forall\,f\colon\mathbb{R}^{n+1}\to[0,1],\end{align*} $$the corresponding operator ![]() $\overline {S}$ from the second variation of the Euclidean heat content satisfies
$\overline {S}$ from the second variation of the Euclidean heat content satisfies
 $$ \begin{align*}\overline{S}(f)(x)\colon= t^{(n+1)/2}(2\pi)^{-(n+1)/2}\int_{\Sigma}f(y)e^{-\frac{\left\|y- x\right\|^{2}}{2t}}\,\mathrm{d} y,\qquad\forall\,x\in\Sigma, \end{align*} $$
$$ \begin{align*}\overline{S}(f)(x)\colon= t^{(n+1)/2}(2\pi)^{-(n+1)/2}\int_{\Sigma}f(y)e^{-\frac{\left\|y- x\right\|^{2}}{2t}}\,\mathrm{d} y,\qquad\forall\,x\in\Sigma, \end{align*} $$and then the analogue of (9) for ![]() $f(x)\colon =\langle v,N(x)\rangle $ is
$f(x)\colon =\langle v,N(x)\rangle $ is
so that the second variation corresponding to ![]() $f=\langle v,N\rangle $ is automatically zero. This fact is expected, because a translation does not change the Euclidean heat content. However, this example demonstrates that the key property of the above proof is exactly (10). More specifically, f is an ‘almost eigenfunction’ of S with ‘eigenvalue’
$f=\langle v,N\rangle $ is automatically zero. This fact is expected, because a translation does not change the Euclidean heat content. However, this example demonstrates that the key property of the above proof is exactly (10). More specifically, f is an ‘almost eigenfunction’ of S with ‘eigenvalue’ ![]() $1/\rho $ that is larger than
$1/\rho $ that is larger than ![]() $1$. It seems plausible that other semigroups could also satisfy an identity such as (10), because (10) seems related to hypercontractivity. We leave this open for further research.
$1$. It seems plausible that other semigroups could also satisfy an identity such as (10), because (10) seems related to hypercontractivity. We leave this open for further research.
2 Existence and Regularity
2.1 Preliminaries and Notation
We say that ![]() $\Sigma \subseteq \mathbb {R}^{n+1}$ is an n-dimensional
$\Sigma \subseteq \mathbb {R}^{n+1}$ is an n-dimensional ![]() $C^{\infty }$ manifold with boundary if
$C^{\infty }$ manifold with boundary if ![]() $\Sigma $ can be locally written as the graph of a
$\Sigma $ can be locally written as the graph of a ![]() $C^{\infty }$ function on a relatively open subset of
$C^{\infty }$ function on a relatively open subset of ![]() $\{(x_{1},\ldots ,x_{n})\in \mathbb {R}^{n}\colon x_{n}\geq 0\}$. For any
$\{(x_{1},\ldots ,x_{n})\in \mathbb {R}^{n}\colon x_{n}\geq 0\}$. For any ![]() $(n+1)$-dimensional
$(n+1)$-dimensional ![]() $C^{\infty }$ manifold
$C^{\infty }$ manifold ![]() $\Omega \subseteq \mathbb {R}^{n+1}$ such that
$\Omega \subseteq \mathbb {R}^{n+1}$ such that ![]() $\partial \Omega $ itself has a boundary, we denote
$\partial \Omega $ itself has a boundary, we denote
 $$ \begin{align} \begin{aligned} C_{0}^{\infty}(\Omega;\mathbb{R}^{n+1}) &\colon =\{f\colon \Omega\to\mathbb{R}^{n+1}\colon f\in C^{\infty}(\Omega;\mathbb{R}^{n+1}),\, f(\partial\partial \Omega)=0,\\ &\qquad\qquad\qquad\exists\,r>0,\,f(\Omega\cap(B(0,r))^{c})=0\}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} C_{0}^{\infty}(\Omega;\mathbb{R}^{n+1}) &\colon =\{f\colon \Omega\to\mathbb{R}^{n+1}\colon f\in C^{\infty}(\Omega;\mathbb{R}^{n+1}),\, f(\partial\partial \Omega)=0,\\ &\qquad\qquad\qquad\exists\,r>0,\,f(\Omega\cap(B(0,r))^{c})=0\}. \end{aligned} \end{align} $$We also denote ![]() $C_{0}^{\infty }(\Omega )\colon = C_{0}^{\infty }(\Omega ;\mathbb {R})$. We let
$C_{0}^{\infty }(\Omega )\colon = C_{0}^{\infty }(\Omega ;\mathbb {R})$. We let ![]() $\mathrm {div}$ denote the divergence of a vector field in
$\mathrm {div}$ denote the divergence of a vector field in ![]() $\mathbb {R}^{n+1}$. For any
$\mathbb {R}^{n+1}$. For any ![]() $r>0$ and for any
$r>0$ and for any ![]() $x\in \mathbb {R}^{n+1}$, we let
$x\in \mathbb {R}^{n+1}$, we let ![]() $B(x,r)\colon =\{y\in \mathbb {R}^{n+1}\colon \left \|x-y\right \|\leq r\}$ be the closed Euclidean ball of radius r centred at
$B(x,r)\colon =\{y\in \mathbb {R}^{n+1}\colon \left \|x-y\right \|\leq r\}$ be the closed Euclidean ball of radius r centred at ![]() $x\in \mathbb {R}^{n+1}$. Here
$x\in \mathbb {R}^{n+1}$. Here ![]() $\partial \partial \Omega $ refers to the
$\partial \partial \Omega $ refers to the ![]() $(n-1)$-dimensional boundary of
$(n-1)$-dimensional boundary of ![]() $\Omega $.
$\Omega $.
Definition 2.1 Reduced Boundary
A measurable set ![]() $\Omega \subseteq \mathbb {R}^{n+1}$ has locally finite surface area if, for any
$\Omega \subseteq \mathbb {R}^{n+1}$ has locally finite surface area if, for any ![]() $r>0$,
$r>0$,
 $$ \begin{align*}\sup\left\{\int_{\Omega}\mathrm{div}(X(x))\,\mathrm{d} x\colon X\in C_{0}^{\infty}(B(0,r),\mathbb{R}^{n+1}),\, \sup_{x\in\mathbb{R}^{n+1}}\left\|X(x)\right\|\leq1\right\}<\infty.\end{align*} $$
$$ \begin{align*}\sup\left\{\int_{\Omega}\mathrm{div}(X(x))\,\mathrm{d} x\colon X\in C_{0}^{\infty}(B(0,r),\mathbb{R}^{n+1}),\, \sup_{x\in\mathbb{R}^{n+1}}\left\|X(x)\right\|\leq1\right\}<\infty.\end{align*} $$Equivalently, ![]() $\Omega $ has locally finite surface area if
$\Omega $ has locally finite surface area if ![]() $\nabla 1_{\Omega }$ is a vector-valued Radon measure such that, for any
$\nabla 1_{\Omega }$ is a vector-valued Radon measure such that, for any ![]() $x\in \mathbb {R}^{n+1}$, the total variation
$x\in \mathbb {R}^{n+1}$, the total variation
 $$ \begin{align*}\left\|\nabla 1_{\Omega}\right\|(B(x,1)) \colon=\sup_{\substack{\mathrm{partitions}\\ C_{1},\ldots,C_{m}\,\mathrm{of}\,B(x,1) \\ m\geq1}}\sum_{i=1}^{m}\left\|\nabla 1_{\Omega}(C_{i})\right\| \end{align*} $$
$$ \begin{align*}\left\|\nabla 1_{\Omega}\right\|(B(x,1)) \colon=\sup_{\substack{\mathrm{partitions}\\ C_{1},\ldots,C_{m}\,\mathrm{of}\,B(x,1) \\ m\geq1}}\sum_{i=1}^{m}\left\|\nabla 1_{\Omega}(C_{i})\right\| \end{align*} $$is finite [Reference Cicalese and LeonardiCL12]. If ![]() $\Omega \subseteq \mathbb {R}^{n+1}$ has locally finite surface area, we define the reduced boundary
$\Omega \subseteq \mathbb {R}^{n+1}$ has locally finite surface area, we define the reduced boundary ![]() $\partial ^{*} \Omega $ of
$\partial ^{*} \Omega $ of ![]() $\Omega $ to be the set of points
$\Omega $ to be the set of points ![]() $x\in \mathbb {R}^{n+1}$ such that
$x\in \mathbb {R}^{n+1}$ such that
 $$ \begin{align*}N(x)\colon=-\lim_{r\to0^{+}}\frac{\nabla 1_{\Omega}(B(x,r))}{\left\|\nabla 1_{\Omega}\right\|(B(x,r))}\end{align*} $$
$$ \begin{align*}N(x)\colon=-\lim_{r\to0^{+}}\frac{\nabla 1_{\Omega}(B(x,r))}{\left\|\nabla 1_{\Omega}\right\|(B(x,r))}\end{align*} $$exists, and it is exactly one element of ![]() $S^{n}\colon =\{x\in \mathbb {R}^{n+1}\colon \left \|x\right \|=1\}$.
$S^{n}\colon =\{x\in \mathbb {R}^{n+1}\colon \left \|x\right \|=1\}$.
The reduced boundary ![]() $\partial ^{*}\Omega $ is a subset of the topological boundary
$\partial ^{*}\Omega $ is a subset of the topological boundary ![]() $\partial \Omega $. Also,
$\partial \Omega $. Also, ![]() $\partial ^{*}\Omega $ and
$\partial ^{*}\Omega $ and ![]() $\partial \Omega $ coincide with the support of
$\partial \Omega $ coincide with the support of ![]() $\nabla 1_{\Omega }$, except for a set of n-dimensional Hausdorff measure zero.
$\nabla 1_{\Omega }$, except for a set of n-dimensional Hausdorff measure zero.
Let ![]() $\Omega \subseteq \mathbb {R}^{n+1}$ be an
$\Omega \subseteq \mathbb {R}^{n+1}$ be an ![]() $(n+1)$-dimensional
$(n+1)$-dimensional ![]() $C^{2}$ submanifold with reduced boundary
$C^{2}$ submanifold with reduced boundary ![]() $\Sigma \colon =\partial ^{*} \Omega $. Let
$\Sigma \colon =\partial ^{*} \Omega $. Let ![]() $N\colon \Sigma \to S^{n}$ be the unit exterior normal to
$N\colon \Sigma \to S^{n}$ be the unit exterior normal to ![]() $\Sigma $. Let
$\Sigma $. Let  $X\in C_{0}^{\infty }(\mathbb {R}^{n+1},\mathbb {R}^{n+1})$. We write X in its components as
$X\in C_{0}^{\infty }(\mathbb {R}^{n+1},\mathbb {R}^{n+1})$. We write X in its components as ![]() $X=(X_{1},\ldots ,X_{n+1})$, so that
$X=(X_{1},\ldots ,X_{n+1})$, so that  $\mathrm {div}X=\sum _{i=1}^{n+1}\frac {\partial }{\partial x_{i}}X_{i}$. Let
$\mathrm {div}X=\sum _{i=1}^{n+1}\frac {\partial }{\partial x_{i}}X_{i}$. Let ![]() $\Psi \colon \mathbb {R}^{n+1}\times (-1,1)\to \mathbb {R}^{n+1}$ such that
$\Psi \colon \mathbb {R}^{n+1}\times (-1,1)\to \mathbb {R}^{n+1}$ such that
 $$ \begin{align} \Psi(x,0)=x,\qquad\qquad\frac{\mathrm{d}}{\mathrm{d} s}\Psi(x,s)=X(\Psi(x,s)),\quad\forall\,x\in\mathbb{R}^{n+1},\,s\in(-1,1). \end{align} $$
$$ \begin{align} \Psi(x,0)=x,\qquad\qquad\frac{\mathrm{d}}{\mathrm{d} s}\Psi(x,s)=X(\Psi(x,s)),\quad\forall\,x\in\mathbb{R}^{n+1},\,s\in(-1,1). \end{align} $$For any ![]() $s\in (-1,1)$, let
$s\in (-1,1)$, let ![]() $\Omega ^{(s)}\colon =\Psi (\Omega ,s)$. Note that
$\Omega ^{(s)}\colon =\Psi (\Omega ,s)$. Note that ![]() $\Omega ^{(0)}=\Omega $. Let
$\Omega ^{(0)}=\Omega $. Let ![]() $\Sigma ^{(s)}\colon =\partial ^{*}\Omega ^{(s)}$,
$\Sigma ^{(s)}\colon =\partial ^{*}\Omega ^{(s)}$, ![]() $\forall \ s\in (-1,1)$.
$\forall \ s\in (-1,1)$.
Definition 2.2. We call 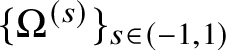 $\{\Omega ^{(s)}\}_{s\in (-1,1)}$ as defined above a variation of
$\{\Omega ^{(s)}\}_{s\in (-1,1)}$ as defined above a variation of ![]() $\Omega \subseteq \mathbb {R}^{n+1}$. We also call
$\Omega \subseteq \mathbb {R}^{n+1}$. We also call 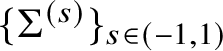 $\{\Sigma ^{(s)}\}_{s\in (-1,1)}$ a variation of
$\{\Sigma ^{(s)}\}_{s\in (-1,1)}$ a variation of ![]() $\Sigma =\partial ^{*}\Omega $.
$\Sigma =\partial ^{*}\Omega $.
For any ![]() $x\in \mathbb {R}^{n+1}$ and any
$x\in \mathbb {R}^{n+1}$ and any ![]() $s\in (-1,1)$, define
$s\in (-1,1)$, define
 $$ \begin{align} V(x,s)\colon=\int_{\Omega^{(s)}}G(x,y)\,\mathrm{d} y. \end{align} $$
$$ \begin{align} V(x,s)\colon=\int_{\Omega^{(s)}}G(x,y)\,\mathrm{d} y. \end{align} $$ Below, when appropriate, we let ![]() $\,\mathrm {d} x$ denote Lebesgue measure, restricted to a surface
$\,\mathrm {d} x$ denote Lebesgue measure, restricted to a surface ![]() $\Sigma \subseteq \mathbb {R}^{n+1}$.
$\Sigma \subseteq \mathbb {R}^{n+1}$.
Lemma 2.3 Existence of a Maximiser
Let ![]() $0<\rho <1$ and let
$0<\rho <1$ and let ![]() $m\geq 2$. Then there exist measurable sets
$m\geq 2$. Then there exist measurable sets ![]() $\Omega _{1},\ldots ,\Omega _{m}$ maximising Problem 1.5.
$\Omega _{1},\ldots ,\Omega _{m}$ maximising Problem 1.5.
Proof. Define ![]() $\Delta _{m}$ as in (6). Let
$\Delta _{m}$ as in (6). Let ![]() $f\colon \mathbb {R}^{n+1}\to \Delta _{m}$. We write f in its components as
$f\colon \mathbb {R}^{n+1}\to \Delta _{m}$. We write f in its components as ![]() $f=(f_{1},\ldots ,f_{m})$. The set
$f=(f_{1},\ldots ,f_{m})$. The set ![]() $D_{0}\colon =\{f\colon \mathbb {R}^{n+1}\to \Delta _{m}\}$ is norm closed, bounded and convex; therefore, it is weakly compact and convex. Consider the function
$D_{0}\colon =\{f\colon \mathbb {R}^{n+1}\to \Delta _{m}\}$ is norm closed, bounded and convex; therefore, it is weakly compact and convex. Consider the function
 $$ \begin{align*}C(f)\colon=\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}}f_{i}(x)T_{\rho}f_{i}(x)\gamma_{n+1}(x)\,\mathrm{d} x.\end{align*} $$
$$ \begin{align*}C(f)\colon=\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}}f_{i}(x)T_{\rho}f_{i}(x)\gamma_{n+1}(x)\,\mathrm{d} x.\end{align*} $$This function is weakly continuous on ![]() $D_{0}$, and
$D_{0}$, and ![]() $D_{0}$ is weakly compact, so there exists
$D_{0}$ is weakly compact, so there exists ![]() $\widetilde {f}\in D_{0}$ such that
$\widetilde {f}\in D_{0}$ such that  $C(\widetilde {f})=\max _{f\in D_{0}}C(f)$. Moreover, C is convex because for any
$C(\widetilde {f})=\max _{f\in D_{0}}C(f)$. Moreover, C is convex because for any ![]() $0<t<1$ and for any
$0<t<1$ and for any ![]() $f,g\in D_{0}$,
$f,g\in D_{0}$,
 $$ \begin{align*} &tC(f)+(1-t)C(g)-C(tf+(1-t)g)\\ &\qquad=\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}} \Big(tf_{i}(x)T_{\rho}f_{i}(x)+(1-t)g_{i}(x)T_{\rho}g_{i}(x)\\ &\qquad\qquad\qquad\qquad\qquad-(tf_{i}(x)+(1-t)g_{i}(x))T_{\rho}[tf_{i}(x)+(1-t)g_{i}(x)] \Big)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad=t(1-t)\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}} \Big((f_{i}(x)-g_{i}(x))T_{\rho}[f_{i}(x)-g_{i}(x)]\Big)\gamma_{n+1}(x)\,\mathrm{d} x \geq0. \end{align*} $$
$$ \begin{align*} &tC(f)+(1-t)C(g)-C(tf+(1-t)g)\\ &\qquad=\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}} \Big(tf_{i}(x)T_{\rho}f_{i}(x)+(1-t)g_{i}(x)T_{\rho}g_{i}(x)\\ &\qquad\qquad\qquad\qquad\qquad-(tf_{i}(x)+(1-t)g_{i}(x))T_{\rho}[tf_{i}(x)+(1-t)g_{i}(x)] \Big)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad=t(1-t)\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}} \Big((f_{i}(x)-g_{i}(x))T_{\rho}[f_{i}(x)-g_{i}(x)]\Big)\gamma_{n+1}(x)\,\mathrm{d} x \geq0. \end{align*} $$Here we used that
 $$ \begin{align} \int_{\mathbb{R}^{n+1}} h(x)T_{\rho}h(x)\gamma_{n+1}(x)\,\mathrm{d} x=\int_{\mathbb{R}^{n+1}} (T_{\sqrt{\rho}}h(x))^{2}\gamma_{n+1}(x)\,\mathrm{d} x\geq0, \end{align} $$
$$ \begin{align} \int_{\mathbb{R}^{n+1}} h(x)T_{\rho}h(x)\gamma_{n+1}(x)\,\mathrm{d} x=\int_{\mathbb{R}^{n+1}} (T_{\sqrt{\rho}}h(x))^{2}\gamma_{n+1}(x)\,\mathrm{d} x\geq0, \end{align} $$for all measurable ![]() $h\colon \mathbb {R}^{n+1}\to [-1,1]$.
$h\colon \mathbb {R}^{n+1}\to [-1,1]$.
Because C is convex, its maximum must be achieved at an extreme point of ![]() $D_{0}$. Let
$D_{0}$. Let ![]() $e_{1},\ldots ,e_{m}$ denote the standard basis of
$e_{1},\ldots ,e_{m}$ denote the standard basis of ![]() $\mathbb {R}^{m}$, so that f takes its values in
$\mathbb {R}^{m}$, so that f takes its values in ![]() $\{e_{1},\ldots ,e_{m}\}$. Then, for any
$\{e_{1},\ldots ,e_{m}\}$. Then, for any ![]() $1\leq i\leq m$, define
$1\leq i\leq m$, define ![]() $\Omega _{i}\colon =\{x\in \mathbb {R}^{n+1}\colon f(x)=e_{i}\}$, so that
$\Omega _{i}\colon =\{x\in \mathbb {R}^{n+1}\colon f(x)=e_{i}\}$, so that ![]() $f_{i}=1_{\Omega _{i}}\ \forall \ 1\leq i\leq m$.
$f_{i}=1_{\Omega _{i}}\ \forall \ 1\leq i\leq m$.
Lemma 2.4 Regularity of a Maximiser
Let ![]() $\Omega _{1},\ldots ,\Omega _{m}\subseteq \mathbb {R}^{n+1}$ be the measurable sets maximising Problem 1.5, guaranteed to exist by Lemma 2.3. Then the sets
$\Omega _{1},\ldots ,\Omega _{m}\subseteq \mathbb {R}^{n+1}$ be the measurable sets maximising Problem 1.5, guaranteed to exist by Lemma 2.3. Then the sets ![]() $\Omega _{1},\ldots ,\Omega _{m}$ have locally finite surface area. Moreover, for all
$\Omega _{1},\ldots ,\Omega _{m}$ have locally finite surface area. Moreover, for all ![]() $1\leq i\leq m$ and for all
$1\leq i\leq m$ and for all ![]() $x\in \partial \Omega _{i}$, there exists a neighbourhood U of x such that
$x\in \partial \Omega _{i}$, there exists a neighbourhood U of x such that ![]() $U\cap \partial \Omega _{i}$ is a finite union of
$U\cap \partial \Omega _{i}$ is a finite union of ![]() $C^{\infty } \ n$-dimensional manifolds.
$C^{\infty } \ n$-dimensional manifolds.
Proof. This follows from a first variation argument and the strong unique continuation property for the heat equation. We first claim that there exist constants ![]() $(c_{ij})_{1\leq i<j\leq m}$ such that
$(c_{ij})_{1\leq i<j\leq m}$ such that
 $$ \begin{align} \Omega_{i}\supseteq\{x\in\mathbb{R}^{n+1}\colon T_{\rho}1_{\Omega_{i}}(x)>T_{\rho}1_{\Omega_{j}}(x)+c_{ij},\,\forall\,j\in\{1,\ldots,m\}\setminus\{i\}\},\qquad\forall\,1\leq i\leq m. \end{align} $$
$$ \begin{align} \Omega_{i}\supseteq\{x\in\mathbb{R}^{n+1}\colon T_{\rho}1_{\Omega_{i}}(x)>T_{\rho}1_{\Omega_{j}}(x)+c_{ij},\,\forall\,j\in\{1,\ldots,m\}\setminus\{i\}\},\qquad\forall\,1\leq i\leq m. \end{align} $$ By the Lebesgue density theorem [Reference SteinSte70, 1.2.1, Proposition 1], we may assume that, for all ![]() $i\in \{1,\ldots ,k\}$, if
$i\in \{1,\ldots ,k\}$, if ![]() $y\in \Omega _{i}$, then we have
$y\in \Omega _{i}$, then we have ![]() $\lim _{r\to 0}\gamma _{n+1}(\Omega _{i}\cap B(y,r))/\gamma _{n+1}(B(y,r))=1$.
$\lim _{r\to 0}\gamma _{n+1}(\Omega _{i}\cap B(y,r))/\gamma _{n+1}(B(y,r))=1$.
We prove (16) by contradiction. Suppose there exist ![]() $c\in \mathbb {R}$,
$c\in \mathbb {R}$, ![]() $j,k\in \{1,\ldots ,m\}$ with
$j,k\in \{1,\ldots ,m\}$ with ![]() $j\neq k$ and there exists
$j\neq k$ and there exists ![]() $y\in \Omega _{j}$ and
$y\in \Omega _{j}$ and ![]() $z\in \Omega _{k}$ such that
$z\in \Omega _{k}$ such that
By (3), ![]() $T_{\rho }(1_{\Omega _{j}}-1_{\Omega _{k}})(x)$ is a continuous function of x. And by the Lebesgue density theorem, there exist disjoint measurable sets
$T_{\rho }(1_{\Omega _{j}}-1_{\Omega _{k}})(x)$ is a continuous function of x. And by the Lebesgue density theorem, there exist disjoint measurable sets ![]() $U_{j},U_{k}$ with positive Lebesgue measure such that
$U_{j},U_{k}$ with positive Lebesgue measure such that ![]() $U_{j}\subseteq \Omega _{j},U_{k}\subseteq \Omega _{k}$ such that
$U_{j}\subseteq \Omega _{j},U_{k}\subseteq \Omega _{k}$ such that ![]() $\gamma _{n+1}(U_{j})=\gamma _{n+1}(U_{k})$ and such that
$\gamma _{n+1}(U_{j})=\gamma _{n+1}(U_{k})$ and such that
We define a new partition of ![]() $\mathbb {R}^{n+1}$ such that
$\mathbb {R}^{n+1}$ such that 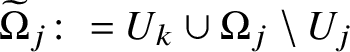 $\widetilde {\Omega }_{j}\colon = U_{k}\cup \Omega _{j}\setminus U_{j}$,
$\widetilde {\Omega }_{j}\colon = U_{k}\cup \Omega _{j}\setminus U_{j}$, 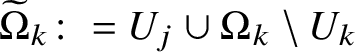 $\widetilde {\Omega }_{k}\colon = U_{j}\cup \Omega _{k}\setminus U_{k}$ and
$\widetilde {\Omega }_{k}\colon = U_{j}\cup \Omega _{k}\setminus U_{k}$ and ![]() $\widetilde {\Omega }_{i}\colon =\Omega _{i}$ for all
$\widetilde {\Omega }_{i}\colon =\Omega _{i}$ for all ![]() $i\in \{1,\ldots ,m\}\setminus \{j,k\}$. Then
$i\in \{1,\ldots ,m\}\setminus \{j,k\}$. Then
 $$ \begin{align*} &\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}}1_{\widetilde{\Omega}_{i}}(x)T_{\rho}1_{\widetilde{\Omega}_{i}}(x)\gamma_{n+1}(x)\,\mathrm{d} x -\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}}1_{\Omega_{i}}(x)T_{\rho}1_{\Omega_{i}}(x)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad=\int_{\mathbb{R}^{n+1}}1_{\widetilde{\Omega}_{j}}(x)T_{\rho}1_{\widetilde{\Omega}_{j}}(x)\gamma_{n+1}(x)\,\mathrm{d} x -\int_{\mathbb{R}^{n+1}}1_{\Omega_{j}}(x)T_{\rho}1_{\Omega_{j}}(x)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad\qquad+\int_{\mathbb{R}^{n+1}}1_{\widetilde{\Omega}_{k}}(x)T_{\rho}1_{\widetilde{\Omega}_{k}}(x)\gamma_{n+1}(x)\,\mathrm{d} x -\int_{\mathbb{R}^{n+1}}1_{\Omega_{k}}(x)T_{\rho}1_{\Omega_{k}}(x)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad=\int_{\mathbb{R}^{n+1}}[1_{\Omega_{j}}-1_{U_{j}}+1_{U_{k}}](x)T_{\rho}[1_{\Omega_{j}}-1_{U_{j}}+1_{U_{k}}]\gamma_{n+1}(x)\,\mathrm{d} x \\ &\qquad\qquad\qquad+\int_{\mathbb{R}^{n+1}}[1_{\Omega_{k}}-1_{U_{k}}+1_{U_{j}}]T_{\rho}[1_{\Omega_{k}}-1_{U_{k}}+1_{U_{j}}]\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad\qquad-\int_{\mathbb{R}^{n+1}}1_{\Omega_{j}}(x)T_{\rho}1_{\Omega_{j}}(x)\gamma_{n+1}(x)\,\mathrm{d} x-\int_{\mathbb{R}^{n+1}}1_{\Omega_{k}}(x)T_{\rho}1_{\Omega_{k}}(x)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad=2\int_{\mathbb{R}^{n+1}}[-1_{U_{j}}+1_{U_{k}}](x)T_{\rho}[1_{\Omega_{j}}-1_{\Omega_{k}}]\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad\qquad+2\int_{\mathbb{R}^{n+1}}[1_{U_{j}}-1_{U_{k}}]T_{\rho}[1_{U_{j}}-1_{U_{k}}]\gamma_{n+1}(x)\,\mathrm{d} x \stackrel{(17)\wedge(15)}{>}0. \end{align*} $$
$$ \begin{align*} &\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}}1_{\widetilde{\Omega}_{i}}(x)T_{\rho}1_{\widetilde{\Omega}_{i}}(x)\gamma_{n+1}(x)\,\mathrm{d} x -\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}}1_{\Omega_{i}}(x)T_{\rho}1_{\Omega_{i}}(x)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad=\int_{\mathbb{R}^{n+1}}1_{\widetilde{\Omega}_{j}}(x)T_{\rho}1_{\widetilde{\Omega}_{j}}(x)\gamma_{n+1}(x)\,\mathrm{d} x -\int_{\mathbb{R}^{n+1}}1_{\Omega_{j}}(x)T_{\rho}1_{\Omega_{j}}(x)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad\qquad+\int_{\mathbb{R}^{n+1}}1_{\widetilde{\Omega}_{k}}(x)T_{\rho}1_{\widetilde{\Omega}_{k}}(x)\gamma_{n+1}(x)\,\mathrm{d} x -\int_{\mathbb{R}^{n+1}}1_{\Omega_{k}}(x)T_{\rho}1_{\Omega_{k}}(x)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad=\int_{\mathbb{R}^{n+1}}[1_{\Omega_{j}}-1_{U_{j}}+1_{U_{k}}](x)T_{\rho}[1_{\Omega_{j}}-1_{U_{j}}+1_{U_{k}}]\gamma_{n+1}(x)\,\mathrm{d} x \\ &\qquad\qquad\qquad+\int_{\mathbb{R}^{n+1}}[1_{\Omega_{k}}-1_{U_{k}}+1_{U_{j}}]T_{\rho}[1_{\Omega_{k}}-1_{U_{k}}+1_{U_{j}}]\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad\qquad-\int_{\mathbb{R}^{n+1}}1_{\Omega_{j}}(x)T_{\rho}1_{\Omega_{j}}(x)\gamma_{n+1}(x)\,\mathrm{d} x-\int_{\mathbb{R}^{n+1}}1_{\Omega_{k}}(x)T_{\rho}1_{\Omega_{k}}(x)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad=2\int_{\mathbb{R}^{n+1}}[-1_{U_{j}}+1_{U_{k}}](x)T_{\rho}[1_{\Omega_{j}}-1_{\Omega_{k}}]\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad\qquad+2\int_{\mathbb{R}^{n+1}}[1_{U_{j}}-1_{U_{k}}]T_{\rho}[1_{U_{j}}-1_{U_{k}}]\gamma_{n+1}(x)\,\mathrm{d} x \stackrel{(17)\wedge(15)}{>}0. \end{align*} $$This contradicts the maximality of ![]() $\Omega _{1},\ldots ,\Omega _{m}$. We conclude that (16) holds.
$\Omega _{1},\ldots ,\Omega _{m}$. We conclude that (16) holds.
We now fix ![]() $1\leq i<j\leq m$ and we upgrade (16) by examining the level sets of
$1\leq i<j\leq m$ and we upgrade (16) by examining the level sets of
 $$ \begin{align*} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x),\qquad\forall\,x\in\mathbb{R}^{n+1}. \end{align*} $$
$$ \begin{align*} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x),\qquad\forall\,x\in\mathbb{R}^{n+1}. \end{align*} $$Fix ![]() $c\in \mathbb {R}$ and consider the level set
$c\in \mathbb {R}$ and consider the level set
 $$ \begin{align*}\Sigma\colon=\{x\in\mathbb{R}^{n+1}\colon T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)=c \}.\end{align*} $$
$$ \begin{align*}\Sigma\colon=\{x\in\mathbb{R}^{n+1}\colon T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)=c \}.\end{align*} $$This level set has Hausdorff dimension at most n by [Reference ChenChe98, Theorem 2.3].
From the strong unique continuation property for the heat equation [Reference LinLin90], ![]() $T_{\rho }(1_{\Omega _{i}}-1_{\Omega _{j}})(x)$ does not vanish to infinite order at any
$T_{\rho }(1_{\Omega _{i}}-1_{\Omega _{j}})(x)$ does not vanish to infinite order at any ![]() $x\in \mathbb {R}^{n+1}$, so the argument of [Reference Hardt and SimonHS89, Lemma 1.9] (see [Reference Han and LinHL94, Proposition 1.2] and also [Reference ChenChe98, Theorem 2.1]) shows that in a neighbourhood of each
$x\in \mathbb {R}^{n+1}$, so the argument of [Reference Hardt and SimonHS89, Lemma 1.9] (see [Reference Han and LinHL94, Proposition 1.2] and also [Reference ChenChe98, Theorem 2.1]) shows that in a neighbourhood of each ![]() $x\in \Sigma $,
$x\in \Sigma $, ![]() $\Sigma $ can be written as a finite union of
$\Sigma $ can be written as a finite union of ![]() $C^{\infty }$ manifolds. That is, there exists a neighbourhood U of x and there exists an integer
$C^{\infty }$ manifolds. That is, there exists a neighbourhood U of x and there exists an integer ![]() $k\geq 1$ such that
$k\geq 1$ such that
 $$ \begin{align*}U\cap\Sigma=\cup_{i=1}^{k}\{y\in U\colon D^{i}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\neq 0,\,\, D^{j}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)=0,\,\,\forall\,1\leq j\leq i-1\}.\end{align*} $$
$$ \begin{align*}U\cap\Sigma=\cup_{i=1}^{k}\{y\in U\colon D^{i}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\neq 0,\,\, D^{j}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)=0,\,\,\forall\,1\leq j\leq i-1\}.\end{align*} $$Here ![]() $D^{i}$ denotes the array of all iterated partial derivatives of order
$D^{i}$ denotes the array of all iterated partial derivatives of order ![]() $i\geq 1$. We therefore have
$i\geq 1$. We therefore have
 $$ \begin{align*}\Sigma_{ij}\colon=(\partial^{*}\Omega_{i})\cap(\partial^{*}\Omega_{j})\supseteq\{x\in\mathbb{R}^{n+1}\colon T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)=c_{ij} \},\end{align*} $$
$$ \begin{align*}\Sigma_{ij}\colon=(\partial^{*}\Omega_{i})\cap(\partial^{*}\Omega_{j})\supseteq\{x\in\mathbb{R}^{n+1}\colon T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)=c_{ij} \},\end{align*} $$and the lemma follows.
From Lemma 2.4 and Definition 2.1, for all ![]() $1\leq i<j\leq m$, if
$1\leq i<j\leq m$, if ![]() $x\in \Sigma _{ij}$, then the unit normal vector
$x\in \Sigma _{ij}$, then the unit normal vector ![]() $N_{ij}(x)\in \mathbb {R}^{n+1}$ that points from
$N_{ij}(x)\in \mathbb {R}^{n+1}$ that points from ![]() $\Omega _{i}$ into
$\Omega _{i}$ into ![]() $\Omega _{j}$ is well defined on
$\Omega _{j}$ is well defined on ![]() $\Sigma _{ij}$,
$\Sigma _{ij}$, ![]() $\big ((\partial \Omega _{i})\cap (\partial \Omega _{j})\big )\setminus \Sigma _{ij}$ has Hausdorff dimension at most
$\big ((\partial \Omega _{i})\cap (\partial \Omega _{j})\big )\setminus \Sigma _{ij}$ has Hausdorff dimension at most ![]() $n-1$ and
$n-1$ and
 $$ \begin{align} N_{ij}(x)=\pm\frac{\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)}{\|\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|},\qquad\forall\,x\in\Sigma_{ij}. \end{align} $$
$$ \begin{align} N_{ij}(x)=\pm\frac{\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)}{\|\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|},\qquad\forall\,x\in\Sigma_{ij}. \end{align} $$In Lemma 4.5 we will show that the negative sign holds in (18) when ![]() $\Omega _{1},\ldots ,\Omega _{m}$ maximise Problem 1.5.
$\Omega _{1},\ldots ,\Omega _{m}$ maximise Problem 1.5.
3 First and Second Variation
In this section, we recall some standard facts for variations of sets with respect to the Gaussian measure. Here is a summary of notation.
Summary of Notation.
•
 $T_{\rho }$ denotes the Ornstein–Uhlenbeck operator with correlation parameter
$T_{\rho }$ denotes the Ornstein–Uhlenbeck operator with correlation parameter  $\rho \in (-1,1)$.
$\rho \in (-1,1)$.•
 $\Omega _{1},\ldots ,\Omega _{m}$ denotes a partition of
$\Omega _{1},\ldots ,\Omega _{m}$ denotes a partition of  $\mathbb {R}^{n+1}$ into m disjoint measurable sets.
$\mathbb {R}^{n+1}$ into m disjoint measurable sets.•
 $\partial ^{*}\Omega $ denotes the reduced boundary of
$\partial ^{*}\Omega $ denotes the reduced boundary of  $\Omega \subseteq \mathbb {R}^{n+1}$.
$\Omega \subseteq \mathbb {R}^{n+1}$.•
 $\Sigma _{ij}\colon =(\partial ^{*}\Omega _{i})\cap (\partial ^{*}\Omega _{j})$ for all
$\Sigma _{ij}\colon =(\partial ^{*}\Omega _{i})\cap (\partial ^{*}\Omega _{j})$ for all  $1\leq i,j\leq m$.
$1\leq i,j\leq m$.•
 $N_{ij}(x)$ is the unit normal vector to
$N_{ij}(x)$ is the unit normal vector to  $x\in \Sigma _{ij}$ that points from
$x\in \Sigma _{ij}$ that points from  $\Omega _{i}$ into
$\Omega _{i}$ into  $\Omega _{j}$, so that
$\Omega _{j}$, so that  $N_{ij}=-N_{ji}$.
$N_{ij}=-N_{ji}$.
Throughout the article, unless otherwise stated, we define ![]() $G\colon \mathbb {R}^{n+1}\times \mathbb {R}^{n+1}\to \mathbb {R}$ to be the following function. For all
$G\colon \mathbb {R}^{n+1}\times \mathbb {R}^{n+1}\to \mathbb {R}$ to be the following function. For all ![]() $x,y\in \mathbb {R}^{n+1}, \forall \rho \in (-1,1)$, define
$x,y\in \mathbb {R}^{n+1}, \forall \rho \in (-1,1)$, define
 $$ \begin{align} \begin{aligned} G(x,y)&=(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)}e^{\frac{-\|x\|^{2}-\|y\|^{2}+2\rho\langle x,y\rangle}{2(1-\rho^{2})}}\\ &=(1-\rho^{2})^{-(n+1)/2}\gamma_{n+1}(x)\gamma_{n+1}(y)e^{\frac{-\rho^{2}(\|x\|^{2}+\|y\|^{2})+2\rho\langle x,y\rangle}{2(1-\rho^{2})}}\\ &=(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\gamma_{n+1}(x)e^{\frac{-\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} G(x,y)&=(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)}e^{\frac{-\|x\|^{2}-\|y\|^{2}+2\rho\langle x,y\rangle}{2(1-\rho^{2})}}\\ &=(1-\rho^{2})^{-(n+1)/2}\gamma_{n+1}(x)\gamma_{n+1}(y)e^{\frac{-\rho^{2}(\|x\|^{2}+\|y\|^{2})+2\rho\langle x,y\rangle}{2(1-\rho^{2})}}\\ &=(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\gamma_{n+1}(x)e^{\frac{-\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}. \end{aligned} \end{align} $$We can then rewrite the noise stability from Definition 1.4 as
 $$ \begin{align*}\int_{\mathbb{R}^{n+1}}1_{\Omega}(x)T_{\rho}1_{\Omega}(x)\gamma_{n+1}(x)\,\mathrm{d} x =\int_{\Omega}\int_{\Omega}G(x,y)\,\mathrm{d} x\mathrm{d} y.\end{align*} $$
$$ \begin{align*}\int_{\mathbb{R}^{n+1}}1_{\Omega}(x)T_{\rho}1_{\Omega}(x)\gamma_{n+1}(x)\,\mathrm{d} x =\int_{\Omega}\int_{\Omega}G(x,y)\,\mathrm{d} x\mathrm{d} y.\end{align*} $$Our first and second variation formulas for the noise stability will be written in terms of G.
Lemma 3.1 The First Variation [Reference Choksi and SternbergCS07]; also [Reference Heilman, Mossel and NeemanHMN16, Lemma 3.1, Equation (7)]
Let 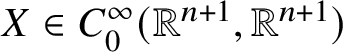 $X\in C_{0}^{\infty }(\mathbb {R}^{n+1},\mathbb {R}^{n+1})$. Let
$X\in C_{0}^{\infty }(\mathbb {R}^{n+1},\mathbb {R}^{n+1})$. Let ![]() $\Omega \subseteq \mathbb {R}^{n+1}$ be a measurable set such that
$\Omega \subseteq \mathbb {R}^{n+1}$ be a measurable set such that ![]() $\partial \Omega $ is a locally finite union of
$\partial \Omega $ is a locally finite union of ![]() $C^{\infty }$ manifolds. Let
$C^{\infty }$ manifolds. Let 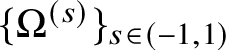 $\{\Omega ^{(s)}\}_{s\in (-1,1)}$ be the corresponding variation of
$\{\Omega ^{(s)}\}_{s\in (-1,1)}$ be the corresponding variation of ![]() $\Omega $. Then
$\Omega $. Then
 $$ \begin{align} \frac{\mathrm{d}}{\mathrm{d} s}\Big|_{s=0}\int_{\mathbb{R}^{n+1}} 1_{\Omega^{(s)}}(y)G(x,y)\,\mathrm{d} y =\int_{\partial \Omega}G(x,y)\langle X(y),N(y)\rangle \,\mathrm{d} y. \end{align} $$
$$ \begin{align} \frac{\mathrm{d}}{\mathrm{d} s}\Big|_{s=0}\int_{\mathbb{R}^{n+1}} 1_{\Omega^{(s)}}(y)G(x,y)\,\mathrm{d} y =\int_{\partial \Omega}G(x,y)\langle X(y),N(y)\rangle \,\mathrm{d} y. \end{align} $$The following lemma is a consequence of (20) and Lemma 2.4.
Lemma 3.2 The First Variation for Maximisers
Suppose that ![]() $\Omega _{1},\ldots ,\Omega _{m}\subseteq \mathbb {R}^{n+1}$ maximise Problem 1.5. Then for all
$\Omega _{1},\ldots ,\Omega _{m}\subseteq \mathbb {R}^{n+1}$ maximise Problem 1.5. Then for all ![]() $1\leq i<j\leq m$, there exists
$1\leq i<j\leq m$, there exists ![]() $c_{ij}\in \mathbb {R}$ such that
$c_{ij}\in \mathbb {R}$ such that
Proof. Fix ![]() $1\leq i<j\leq m$ and denote
$1\leq i<j\leq m$ and denote ![]() $f_{ij}(x)\colon =\langle X(x),N_{ij}(x)\rangle $ for all
$f_{ij}(x)\colon =\langle X(x),N_{ij}(x)\rangle $ for all ![]() $x\in \Sigma _{ij}$. From Lemma 3.1, if X is nonzero outside of
$x\in \Sigma _{ij}$. From Lemma 3.1, if X is nonzero outside of ![]() $\Sigma _{ij}$, we get
$\Sigma _{ij}$, we get
 $$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}}{\mathrm{d} s}\Big|_{s=0}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}}1_{\Omega_{i}^{(s)}}(x)T_{\rho}1_{\Omega_{i}^{(s)}}(x)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad=\int_{\Omega_{i}}G(x,y)\int_{\Sigma_{ij}}\langle X(x),N_{ij}(x)\rangle \,\mathrm{d} x \,\mathrm{d} y +\int_{\Omega_{j}}G(x,y)\int_{\Sigma_{ij}}\langle X(x),N_{ji}(x)\rangle \,\mathrm{d} x \,\mathrm{d} y\\ &\qquad\stackrel{(3)\wedge(19)}{=}\int_{\Sigma_{ij}}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)f_{ij}(x)\,\mathrm{d} x. \end{align*} $$
$$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}}{\mathrm{d} s}\Big|_{s=0}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}}1_{\Omega_{i}^{(s)}}(x)T_{\rho}1_{\Omega_{i}^{(s)}}(x)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad=\int_{\Omega_{i}}G(x,y)\int_{\Sigma_{ij}}\langle X(x),N_{ij}(x)\rangle \,\mathrm{d} x \,\mathrm{d} y +\int_{\Omega_{j}}G(x,y)\int_{\Sigma_{ij}}\langle X(x),N_{ji}(x)\rangle \,\mathrm{d} x \,\mathrm{d} y\\ &\qquad\stackrel{(3)\wedge(19)}{=}\int_{\Sigma_{ij}}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)f_{ij}(x)\,\mathrm{d} x. \end{align*} $$We used above ![]() $N_{ij}=-N_{ji}$. If
$N_{ij}=-N_{ji}$. If ![]() $T_{\rho }(1_{\Omega _{i}}-1_{\Omega _{j}})(x)$ is nonconstant, then we can construct
$T_{\rho }(1_{\Omega _{i}}-1_{\Omega _{j}})(x)$ is nonconstant, then we can construct ![]() $f_{ij}$ supported in
$f_{ij}$ supported in ![]() $\Sigma _{ij}$ with
$\Sigma _{ij}$ with  $\int _{\partial ^{*}\Omega _{i'}}f_{ij}(x)\gamma _{n+1}(x)dx=0$ for all
$\int _{\partial ^{*}\Omega _{i'}}f_{ij}(x)\gamma _{n+1}(x)dx=0$ for all ![]() $1\leq i'\leq m$ to give a nonzero derivative, contradicting the maximality of
$1\leq i'\leq m$ to give a nonzero derivative, contradicting the maximality of ![]() $\Omega _{1},\ldots ,\Omega _{m}$ (as in Lemma 2.4 and (17)).
$\Omega _{1},\ldots ,\Omega _{m}$ (as in Lemma 2.4 and (17)).
Theorem 3.3 General Second Variation Formula [Reference Choksi and SternbergCS07, Theorem 2.6]; also [Reference HeilmanHei15, Theorem 1.10]
Let  $X\in C_{0}^{\infty }(\mathbb {R}^{n+1},\mathbb {R}^{n+1})$. Let
$X\in C_{0}^{\infty }(\mathbb {R}^{n+1},\mathbb {R}^{n+1})$. Let ![]() $\Omega \subseteq \mathbb {R}^{n+1}$ be a measurable set such that
$\Omega \subseteq \mathbb {R}^{n+1}$ be a measurable set such that ![]() $\partial \Omega $ is a locally finite union of
$\partial \Omega $ is a locally finite union of ![]() $C^{\infty }$ manifolds. Let
$C^{\infty }$ manifolds. Let  $\{\Omega ^{(s)}\}_{s\in (-1,1)}$ be the corresponding variation of
$\{\Omega ^{(s)}\}_{s\in (-1,1)}$ be the corresponding variation of ![]() $\Omega $. Define V as in (14). Then
$\Omega $. Define V as in (14). Then
 $$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\int_{\mathbb{R}^{n+1}} \int_{\mathbb{R}^{n+1}} 1_{\Omega^{(s)}}(y)G(x,y) 1_{\Omega^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\quad=\int_{\Sigma}\int_{\Sigma}G(x,y)\langle X(x),N(x)\rangle\langle X(y),N(y)\rangle \,\mathrm{d} x\mathrm{d} y +\int_{\Sigma}\mathrm{div}(V(x,0)X(x))\langle X(x),N(x)\rangle \,\mathrm{d} x. \end{align*} $$
$$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\int_{\mathbb{R}^{n+1}} \int_{\mathbb{R}^{n+1}} 1_{\Omega^{(s)}}(y)G(x,y) 1_{\Omega^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\quad=\int_{\Sigma}\int_{\Sigma}G(x,y)\langle X(x),N(x)\rangle\langle X(y),N(y)\rangle \,\mathrm{d} x\mathrm{d} y +\int_{\Sigma}\mathrm{div}(V(x,0)X(x))\langle X(x),N(x)\rangle \,\mathrm{d} x. \end{align*} $$4 Noise Stability and the Calculus of Variations
We now further refine the first and second variation formulas from the previous section. The following formula follows by using ![]() $G(x,y)\colon =\gamma _{n+1}(x)\gamma _{n+1}(y)\ \forall \ x,y\in \mathbb {R}^{n+1}$ in Lemma 3.1 and in Theorem 3.3.
$G(x,y)\colon =\gamma _{n+1}(x)\gamma _{n+1}(y)\ \forall \ x,y\in \mathbb {R}^{n+1}$ in Lemma 3.1 and in Theorem 3.3.
Lemma 4.1 Variations of Gaussian Volume [Reference LedouxLed01]
Let ![]() $\Omega \subseteq \mathbb {R}^{n+1}$ be a measurable set such that
$\Omega \subseteq \mathbb {R}^{n+1}$ be a measurable set such that ![]() $\partial \Omega $ is a locally finite union of
$\partial \Omega $ is a locally finite union of ![]() $C^{\infty }$ manifolds. Let
$C^{\infty }$ manifolds. Let  $X\in C_{0}^{\infty }(\mathbb {R}^{n+1},\mathbb {R}^{n+1})$. Let
$X\in C_{0}^{\infty }(\mathbb {R}^{n+1},\mathbb {R}^{n+1})$. Let  $\{\Omega ^{(s)}\}_{s\in (-1,1)}$ be the corresponding variation of
$\{\Omega ^{(s)}\}_{s\in (-1,1)}$ be the corresponding variation of ![]() $\Omega $. Denote
$\Omega $. Denote ![]() $f(x)\colon =\langle X(x),N(x)\rangle $ for all
$f(x)\colon =\langle X(x),N(x)\rangle $ for all ![]() $x\in \Sigma \colon = \partial ^{*}\Omega $. Then
$x\in \Sigma \colon = \partial ^{*}\Omega $. Then
 $$ \begin{align*}\frac{\mathrm{d}}{\mathrm{d} s}\Big|_{s=0}\gamma_{n+1}(\Omega^{(s)})=\int_{\Sigma}f(x)\gamma_{n+1}(x)\,\mathrm{d} x.\end{align*} $$
$$ \begin{align*}\frac{\mathrm{d}}{\mathrm{d} s}\Big|_{s=0}\gamma_{n+1}(\Omega^{(s)})=\int_{\Sigma}f(x)\gamma_{n+1}(x)\,\mathrm{d} x.\end{align*} $$ $$ \begin{align*}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\gamma_{n+1}(\Omega^{(s)})=\int_{\Sigma}(\mathrm{div}(X)-\langle X,x\rangle)f(x)\gamma_{n+1}(x)\,\mathrm{d} x.\end{align*} $$
$$ \begin{align*}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\gamma_{n+1}(\Omega^{(s)})=\int_{\Sigma}(\mathrm{div}(X)-\langle X,x\rangle)f(x)\gamma_{n+1}(x)\,\mathrm{d} x.\end{align*} $$Lemma 4.2 Extension Lemma for Existence of Volume-Preserving Variations [Reference HeilmanHei18, Lemma 3.9]
Let  $X'\in C_{0}^{\infty }(\mathbb {R}^{n+1},\mathbb {R}^{n+1})$ be a vector field. Define
$X'\in C_{0}^{\infty }(\mathbb {R}^{n+1},\mathbb {R}^{n+1})$ be a vector field. Define ![]() $f_{ij}\colon =\langle X',N_{ij}\rangle \in C_{0}^{\infty }(\Sigma _{ij})$ for all
$f_{ij}\colon =\langle X',N_{ij}\rangle \in C_{0}^{\infty }(\Sigma _{ij})$ for all ![]() $1\leq i<j\leq m$. If
$1\leq i<j\leq m$. If
 $$ \begin{align} \forall\,1\leq i\leq m,\quad \sum_{j\in\{1,\ldots,m\}\setminus\{i\}}\int_{\Sigma_{ij}}f_{ij}(x)\gamma_{n}(x)\,\mathrm{d} x=0, \end{align} $$
$$ \begin{align} \forall\,1\leq i\leq m,\quad \sum_{j\in\{1,\ldots,m\}\setminus\{i\}}\int_{\Sigma_{ij}}f_{ij}(x)\gamma_{n}(x)\,\mathrm{d} x=0, \end{align} $$then ![]() $X'|_{\cup _{1\leq i<j\leq m}\Sigma _{ij}}$ can be extended to a vector field
$X'|_{\cup _{1\leq i<j\leq m}\Sigma _{ij}}$ can be extended to a vector field  $X\in C_{0}^{\infty }(\mathbb {R}^{n+1},\mathbb {R}^{n+1})$ such that the corresponding variations
$X\in C_{0}^{\infty }(\mathbb {R}^{n+1},\mathbb {R}^{n+1})$ such that the corresponding variations  $\{\Omega _{i}^{(s)}\}_{1\leq i\leq m,s\in (-1,1)}$ satisfy
$\{\Omega _{i}^{(s)}\}_{1\leq i\leq m,s\in (-1,1)}$ satisfy
 $$ \begin{align*}\forall\,1\leq i\leq m,\quad\forall\,s\in(-1,1),\quad \gamma_{n+1}(\Omega_{i}^{(s)})=\gamma_{n+1}(\Omega_{i}).\end{align*} $$
$$ \begin{align*}\forall\,1\leq i\leq m,\quad\forall\,s\in(-1,1),\quad \gamma_{n+1}(\Omega_{i}^{(s)})=\gamma_{n+1}(\Omega_{i}).\end{align*} $$Lemma 4.3. Define G as in (19). Let ![]() $f\colon \Sigma \to \mathbb {R}$ be continous and compactly supported. Then
$f\colon \Sigma \to \mathbb {R}$ be continous and compactly supported. Then
 $$ \begin{align*}\int_{\Sigma}\int_{\Sigma}G(x,y)f(x)f(y) \,\mathrm{d} x\mathrm{d} y\geq0. \end{align*} $$
$$ \begin{align*}\int_{\Sigma}\int_{\Sigma}G(x,y)f(x)f(y) \,\mathrm{d} x\mathrm{d} y\geq0. \end{align*} $$Proof. If ![]() $g\colon \mathbb {R}^{n+1}\to \mathbb {R}$ is continuous and compactly supported, then it is well known that
$g\colon \mathbb {R}^{n+1}\to \mathbb {R}$ is continuous and compactly supported, then it is well known that
 $$ \begin{align*}\int_{\Sigma}\int_{\Sigma}G(x,y)g(x)g(y) \,\mathrm{d} x\mathrm{d} y\geq0, \end{align*} $$
$$ \begin{align*}\int_{\Sigma}\int_{\Sigma}G(x,y)g(x)g(y) \,\mathrm{d} x\mathrm{d} y\geq0, \end{align*} $$because, for example,  $\frac {G(x,y)}{\gamma _{n+1(x)}\gamma _{n+1}(y)}$ is the Mehler kernel, which can be written as an (infinite-dimensional) positive semidefinite matrix. That is, there exists an orthonormal basis
$\frac {G(x,y)}{\gamma _{n+1(x)}\gamma _{n+1}(y)}$ is the Mehler kernel, which can be written as an (infinite-dimensional) positive semidefinite matrix. That is, there exists an orthonormal basis ![]() $\{\psi _{i}\}_{i=1}^{\infty }$ of
$\{\psi _{i}\}_{i=1}^{\infty }$ of ![]() $L_{2}(\gamma _{n+1})$ (of Hermite polynomials) and there exists a sequence of nonnegative real numbers
$L_{2}(\gamma _{n+1})$ (of Hermite polynomials) and there exists a sequence of nonnegative real numbers ![]() $\{\lambda _{i}\}_{i=1}^{\infty }$ such that the following series converges absolutely pointwise:
$\{\lambda _{i}\}_{i=1}^{\infty }$ such that the following series converges absolutely pointwise:
 $$ \begin{align*}\frac{G(x,y)}{\gamma_{n+1}(x)\gamma_{n+1}(y)}=\sum_{i=1}^{\infty}\lambda_{i}\psi_{i}(x)\psi_{i}(y),\qquad\forall\,x,y\in\mathbb{R}^{n+1}.\end{align*} $$
$$ \begin{align*}\frac{G(x,y)}{\gamma_{n+1}(x)\gamma_{n+1}(y)}=\sum_{i=1}^{\infty}\lambda_{i}\psi_{i}(x)\psi_{i}(y),\qquad\forall\,x,y\in\mathbb{R}^{n+1}.\end{align*} $$From Mercer’s theorem, this is equivalent to ![]() $\forall \ p\geq 1$, for all
$\forall \ p\geq 1$, for all ![]() $z^{(1)},\ldots ,z^{(p)}\in \mathbb {R}^{n}$, for all
$z^{(1)},\ldots ,z^{(p)}\in \mathbb {R}^{n}$, for all ![]() $\beta _{1},\ldots ,\beta _{p}\in \mathbb {R}$,
$\beta _{1},\ldots ,\beta _{p}\in \mathbb {R}$,
 $$ \begin{align*}\sum_{i,j=1}^{p}\beta_{i}\beta_{j}G(z^{(i)},z^{(j)})\geq0.\end{align*} $$
$$ \begin{align*}\sum_{i,j=1}^{p}\beta_{i}\beta_{j}G(z^{(i)},z^{(j)})\geq0.\end{align*} $$In particular, this holds for all ![]() $z^{(1)},\ldots ,z^{(p)}\in \partial \Omega \subseteq \mathbb {R}^{n+1}$. So, the positive semidefinite property carries over (by restriction) to
$z^{(1)},\ldots ,z^{(p)}\in \partial \Omega \subseteq \mathbb {R}^{n+1}$. So, the positive semidefinite property carries over (by restriction) to ![]() $\partial \Omega $.
$\partial \Omega $.
4.1 Two Sets
For didactic purposes, we first present the second variation of noise stability when ![]() $m=2$ in Conjecture 1.5.
$m=2$ in Conjecture 1.5.
Lemma 4.4 Second Variation of Noise Stability
Let ![]() $\Omega \subseteq \mathbb {R}^{n+1}$ be a measurable set such that
$\Omega \subseteq \mathbb {R}^{n+1}$ be a measurable set such that ![]() $\partial \Omega $ is a locally finite union of
$\partial \Omega $ is a locally finite union of ![]() $C^{\infty }$ manifolds. Let
$C^{\infty }$ manifolds. Let  $X\in C_{0}^{\infty }(\mathbb {R}^{n+1},\mathbb {R}^{n+1})$. Let
$X\in C_{0}^{\infty }(\mathbb {R}^{n+1},\mathbb {R}^{n+1})$. Let  $\{\Omega ^{(s)}\}_{s\in (-1,1)}$ be the corresponding variation of
$\{\Omega ^{(s)}\}_{s\in (-1,1)}$ be the corresponding variation of ![]() $\Omega $. Denote
$\Omega $. Denote ![]() $f(x)\colon =\langle X(x),N(x)\rangle $ for all
$f(x)\colon =\langle X(x),N(x)\rangle $ for all ![]() $x\in \Sigma \colon = \partial ^{*}\Omega $. Then
$x\in \Sigma \colon = \partial ^{*}\Omega $. Then
 $$ \begin{align} \begin{aligned} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\int_{\mathbb{R}^{n+1}}\int_{\mathbb{R}^{n+1}} 1_{\Omega^{(s)}}(y)G(x,y) 1_{\Omega^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y =\int_{\Sigma}\int_{\Sigma}G(x,y)f(x)f(y)\,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad\qquad +\int_{\Sigma}\langle\overline{\nabla} T_{\rho}1_{\Omega}(x),X(x)\rangle f(x) \gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad\qquad +\int_{\Sigma} T_{\rho}1_{\Omega}(x)\Big(\mathrm{div}(X(x))-\langle X(x),x\rangle\Big)f(x)\gamma_{n+1}(x)\,\mathrm{d} x. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\int_{\mathbb{R}^{n+1}}\int_{\mathbb{R}^{n+1}} 1_{\Omega^{(s)}}(y)G(x,y) 1_{\Omega^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y =\int_{\Sigma}\int_{\Sigma}G(x,y)f(x)f(y)\,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad\qquad +\int_{\Sigma}\langle\overline{\nabla} T_{\rho}1_{\Omega}(x),X(x)\rangle f(x) \gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad\qquad +\int_{\Sigma} T_{\rho}1_{\Omega}(x)\Big(\mathrm{div}(X(x))-\langle X(x),x\rangle\Big)f(x)\gamma_{n+1}(x)\,\mathrm{d} x. \end{aligned} \end{align} $$Proof. For all ![]() $x\in \mathbb {R}^{n+1}$, we have
$x\in \mathbb {R}^{n+1}$, we have  $V(x,0)\stackrel {(14)}{=}\int _{\Omega }G(x,y)\,\mathrm {d} y\stackrel {(3)}{=}\gamma _{n+1}(x)T_{\rho }1_{\Omega }(x)$. So, from Theorem 3.3,
$V(x,0)\stackrel {(14)}{=}\int _{\Omega }G(x,y)\,\mathrm {d} y\stackrel {(3)}{=}\gamma _{n+1}(x)T_{\rho }1_{\Omega }(x)$. So, from Theorem 3.3,
 $$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\int_{\mathbb{R}^{n+1}}\int_{\mathbb{R}^{n+1}} 1_{\Omega^{(s)}}(y)G(x,y) 1_{\Omega^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad\qquad\qquad =\int_{\Sigma}\int_{\Sigma}G(x,y)\langle X(x),N(x)\rangle\langle X(y),N(y)\rangle \,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad\qquad\qquad\qquad +\int_{\Sigma}(\sum_{i=1}^{n+1}T_{\rho}1_{\Omega}(x)\frac{\partial}{\partial x_{i}}X_{i}(x)-x_{i}T_{\rho}1_{\Omega}(x)X_{i}(x)\\ &\qquad\qquad\qquad\qquad\qquad\,\,+\frac{\partial}{\partial x_{i}}T_{\rho}1_{\Omega}(x)X_{i}(x))\langle X(x),N(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$
$$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\int_{\mathbb{R}^{n+1}}\int_{\mathbb{R}^{n+1}} 1_{\Omega^{(s)}}(y)G(x,y) 1_{\Omega^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad\qquad\qquad =\int_{\Sigma}\int_{\Sigma}G(x,y)\langle X(x),N(x)\rangle\langle X(y),N(y)\rangle \,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad\qquad\qquad\qquad +\int_{\Sigma}(\sum_{i=1}^{n+1}T_{\rho}1_{\Omega}(x)\frac{\partial}{\partial x_{i}}X_{i}(x)-x_{i}T_{\rho}1_{\Omega}(x)X_{i}(x)\\ &\qquad\qquad\qquad\qquad\qquad\,\,+\frac{\partial}{\partial x_{i}}T_{\rho}1_{\Omega}(x)X_{i}(x))\langle X(x),N(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$That is, (22) holds.
Lemma 4.5 Volume-reserving Second Variation of Maximisers
Suppose that ![]() $\Omega ,\Omega ^{c}\subseteq \mathbb {R}^{n+1}$ maximise Problem 1.5 for
$\Omega ,\Omega ^{c}\subseteq \mathbb {R}^{n+1}$ maximise Problem 1.5 for ![]() $0<\rho <1$ and
$0<\rho <1$ and ![]() $m=2$. Let
$m=2$. Let  $\{\Omega ^{(s)}\}_{s\in (-1,1)}$ be the corresponding variation of
$\{\Omega ^{(s)}\}_{s\in (-1,1)}$ be the corresponding variation of ![]() $\Omega $. Denote
$\Omega $. Denote ![]() $f(x)\colon =\langle X(x),N(x)\rangle $ for all
$f(x)\colon =\langle X(x),N(x)\rangle $ for all ![]() $x\in \Sigma \colon = \partial ^{*}\Omega $. If
$x\in \Sigma \colon = \partial ^{*}\Omega $. If
 $$ \begin{align*}\int_{\Sigma}f(x)\gamma_{n+1}(x)\,\mathrm{d} x=0,\end{align*} $$
$$ \begin{align*}\int_{\Sigma}f(x)\gamma_{n+1}(x)\,\mathrm{d} x=0,\end{align*} $$then there exists an extension of the vector field ![]() $X|_{\Sigma }$ such that the corresponding variation of
$X|_{\Sigma }$ such that the corresponding variation of  $\{\Omega ^{(s)}\}_{s\in (-1,1)}$ satisfies
$\{\Omega ^{(s)}\}_{s\in (-1,1)}$ satisfies
 $$ \begin{align} \begin{aligned} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\int_{\mathbb{R}^{n+1}}\int_{\mathbb{R}^{n+1}} 1_{\Omega^{(s)}}(y)G(x,y) 1_{\Omega^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad =\int_{\Sigma}\int_{\Sigma}G(x,y)f(x)f(y) \,\mathrm{d} x\mathrm{d} y -\int_{\Sigma}\|\overline{\nabla} T_{\rho}1_{\Omega}(x)\|(f(x))^{2} \gamma_{n+1}(x)\,\mathrm{d} x. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\int_{\mathbb{R}^{n+1}}\int_{\mathbb{R}^{n+1}} 1_{\Omega^{(s)}}(y)G(x,y) 1_{\Omega^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad =\int_{\Sigma}\int_{\Sigma}G(x,y)f(x)f(y) \,\mathrm{d} x\mathrm{d} y -\int_{\Sigma}\|\overline{\nabla} T_{\rho}1_{\Omega}(x)\|(f(x))^{2} \gamma_{n+1}(x)\,\mathrm{d} x. \end{aligned} \end{align} $$Moreover,
 $$ \begin{align} \overline{\nabla}T_{\rho}1_{\Omega}(x)=-N(x)\|\overline{\nabla}T_{\rho}1_{\Omega}(x)\|,\qquad\forall\,x\in\Sigma. \end{align} $$
$$ \begin{align} \overline{\nabla}T_{\rho}1_{\Omega}(x)=-N(x)\|\overline{\nabla}T_{\rho}1_{\Omega}(x)\|,\qquad\forall\,x\in\Sigma. \end{align} $$Proof. From Lemma 3.1, ![]() $T_{\rho }1_{\Omega }(x)$ is constant for all
$T_{\rho }1_{\Omega }(x)$ is constant for all ![]() $x\in \Sigma $. So, from Lemma 4.1 and Lemma 4.2, the last term in (22) vanishes; that is,
$x\in \Sigma $. So, from Lemma 4.1 and Lemma 4.2, the last term in (22) vanishes; that is,
 $$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\int_{\mathbb{R}^{n+1}} \int_{\mathbb{R}^{n+1}}1_{\Omega^{(s)}}(y)G(x,y) 1_{\Omega^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad\qquad =\int_{\Sigma}\int_{\Sigma}G(x,y)\langle X(x),N(x)\rangle \langle X(y),N(y)\rangle \,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad\qquad\qquad +\int_{\Sigma}\langle\overline{\nabla} T_{\rho}1_{\Omega}(x),X(x)\rangle \langle X(x),N(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$
$$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\int_{\mathbb{R}^{n+1}} \int_{\mathbb{R}^{n+1}}1_{\Omega^{(s)}}(y)G(x,y) 1_{\Omega^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad\qquad =\int_{\Sigma}\int_{\Sigma}G(x,y)\langle X(x),N(x)\rangle \langle X(y),N(y)\rangle \,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad\qquad\qquad +\int_{\Sigma}\langle\overline{\nabla} T_{\rho}1_{\Omega}(x),X(x)\rangle \langle X(x),N(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$(Here ![]() $\overline {\nabla }$ denotes the gradient in
$\overline {\nabla }$ denotes the gradient in ![]() $\mathbb {R}^{n+1}$.) Because
$\mathbb {R}^{n+1}$.) Because ![]() $T_{\rho }1_{\Omega }(x)$ is constant for all
$T_{\rho }1_{\Omega }(x)$ is constant for all ![]() $x\in \partial \Omega $ by Lemma 3.2,
$x\in \partial \Omega $ by Lemma 3.2,  $\overline {\nabla } T_{\rho }1_{\Omega }(x)$ is parallel to
$\overline {\nabla } T_{\rho }1_{\Omega }(x)$ is parallel to ![]() $N(x)$ for all
$N(x)$ for all ![]() $x\in \partial \Omega $. That is,
$x\in \partial \Omega $. That is,
 $$ \begin{align} \overline{\nabla} T_{\rho}1_{\Omega}(x)=\pm\|\overline{\nabla} T_{\rho}1_{\Omega}(x)\|N(x),\qquad\forall\,x\in\partial\Omega. \end{align} $$
$$ \begin{align} \overline{\nabla} T_{\rho}1_{\Omega}(x)=\pm\|\overline{\nabla} T_{\rho}1_{\Omega}(x)\|N(x),\qquad\forall\,x\in\partial\Omega. \end{align} $$In fact, we must have a negative sign in (25); otherwise, we could find a vector field X supported near ![]() $x\in \partial \Omega $ such that (25) has a positive sign, and then because G is a positive semidefinite function by Lemma 4.3, we would have
$x\in \partial \Omega $ such that (25) has a positive sign, and then because G is a positive semidefinite function by Lemma 4.3, we would have
 $$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\int_{\mathbb{R}^{n+1}}\int_{\mathbb{R}^{n+1}} 1_{\Omega^{(s)}}(y)G(x,y) 1_{\Omega^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad\qquad\qquad\geq\int_{\Sigma}\langle\overline{\nabla} T_{\rho}1_{\Omega}(x),X(x)\rangle \langle X(x),N(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x>0, \end{align*} $$
$$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\int_{\mathbb{R}^{n+1}}\int_{\mathbb{R}^{n+1}} 1_{\Omega^{(s)}}(y)G(x,y) 1_{\Omega^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad\qquad\qquad\geq\int_{\Sigma}\langle\overline{\nabla} T_{\rho}1_{\Omega}(x),X(x)\rangle \langle X(x),N(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x>0, \end{align*} $$a contradiction. In summary,
 $$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\int_{\mathbb{R}^{n+1}}\int_{\mathbb{R}^{n+1}} 1_{\Omega^{(s)}}(y)G(x,y) 1_{\Omega^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad\qquad =\int_{\Sigma}\int_{\Sigma}G(x,y)\langle X(x),N(x)\rangle \langle X(y),N(y)\rangle \,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad\qquad\qquad -\int_{\Sigma}\|\overline{\nabla} T_{\rho}1_{\Omega}(x)\|\langle X(x),N(x)\rangle^{2} \gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$
$$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\int_{\mathbb{R}^{n+1}}\int_{\mathbb{R}^{n+1}} 1_{\Omega^{(s)}}(y)G(x,y) 1_{\Omega^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad\qquad =\int_{\Sigma}\int_{\Sigma}G(x,y)\langle X(x),N(x)\rangle \langle X(y),N(y)\rangle \,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad\qquad\qquad -\int_{\Sigma}\|\overline{\nabla} T_{\rho}1_{\Omega}(x)\|\langle X(x),N(x)\rangle^{2} \gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$4.2 More Than Two Sets
We can now generalise Subsection 4.1 to the case of ![]() $m>2$ sets.
$m>2$ sets.
Lemma 4.6 Second Variation of Noise Stability, Multiple Sets
Let ![]() $\Omega _{1},\ldots ,\Omega _{m}\subseteq \mathbb {R}^{n+1}$ be a partition of
$\Omega _{1},\ldots ,\Omega _{m}\subseteq \mathbb {R}^{n+1}$ be a partition of ![]() $\mathbb {R}^{n+1}$ into measurable sets such that
$\mathbb {R}^{n+1}$ into measurable sets such that ![]() $\partial \Omega _{i}$ is a locally finite union of
$\partial \Omega _{i}$ is a locally finite union of ![]() $C^{\infty }$ manifolds for all
$C^{\infty }$ manifolds for all ![]() $1\leq i\leq m$. Let
$1\leq i\leq m$. Let  $X\in C_{0}^{\infty }(\mathbb {R}^{n+1},\mathbb {R}^{n+1})$. Let
$X\in C_{0}^{\infty }(\mathbb {R}^{n+1},\mathbb {R}^{n+1})$. Let  $\{\Omega _{i}^{(s)}\}_{s\in (-1,1)}$ be the corresponding variation of
$\{\Omega _{i}^{(s)}\}_{s\in (-1,1)}$ be the corresponding variation of ![]() $\Omega _{i}$ for all
$\Omega _{i}$ for all ![]() $1\leq i\leq m$. Denote
$1\leq i\leq m$. Denote ![]() $f_{ij}(x)\colon =\langle X(x),N_{ij}(x)\rangle $ for all
$f_{ij}(x)\colon =\langle X(x),N_{ij}(x)\rangle $ for all ![]() $x\in \Sigma _{ij}\colon = (\partial ^{*}\Omega _{i})\cap (\partial ^{*}\Omega _{j})$. We let N denote the exterior pointing unit normal vector to
$x\in \Sigma _{ij}\colon = (\partial ^{*}\Omega _{i})\cap (\partial ^{*}\Omega _{j})$. We let N denote the exterior pointing unit normal vector to ![]() $\partial ^{*}\Omega _{i}$ for any
$\partial ^{*}\Omega _{i}$ for any ![]() $1\leq i\leq m$. Then
$1\leq i\leq m$. Then
 $$ \begin{align} \begin{aligned} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}} \int_{\mathbb{R}^{n+1}} 1_{\Omega_{i}^{(s)}}(y)G(x,y) 1_{\Omega_{i}^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad =\sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}}\Big[\Big(\int_{\partial^{*}\Omega_{i}}-\int_{\partial^{*}\Omega_{j}}\Big)G(x,y)\langle X(y),N(y)\rangle \,\mathrm{d} y\Big] f_{ij}(x) \,\mathrm{d} x\\ &\qquad\qquad +\int_{\Sigma_{ij}}\langle\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x),X(x)\rangle f_{ij}(x) \gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad +\int_{\Sigma_{ij}} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\Big(\mathrm{div}(X(x))-\langle X(x),x\rangle\Big)f_{ij}(x)\gamma_{n+1}(x)\,\mathrm{d} x. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}} \int_{\mathbb{R}^{n+1}} 1_{\Omega_{i}^{(s)}}(y)G(x,y) 1_{\Omega_{i}^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad =\sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}}\Big[\Big(\int_{\partial^{*}\Omega_{i}}-\int_{\partial^{*}\Omega_{j}}\Big)G(x,y)\langle X(y),N(y)\rangle \,\mathrm{d} y\Big] f_{ij}(x) \,\mathrm{d} x\\ &\qquad\qquad +\int_{\Sigma_{ij}}\langle\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x),X(x)\rangle f_{ij}(x) \gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad +\int_{\Sigma_{ij}} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\Big(\mathrm{div}(X(x))-\langle X(x),x\rangle\Big)f_{ij}(x)\gamma_{n+1}(x)\,\mathrm{d} x. \end{aligned} \end{align} $$Proof. From Lemma 4.4,
 $$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\int_{\mathbb{R}^{n+1}} \int_{\mathbb{R}^{n+1}} 1_{\Omega_{i}^{(s)}}(y)G(x,y) 1_{\Omega_{i}^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad =\int_{\partial^{*}\Omega_{i}}\int_{\partial^{*}\Omega_{i}}G(x,y)\langle X(x),N(x)\rangle \langle X(y),N(y)\rangle \,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad +\int_{\partial^{*}\Omega_{i}}\langle\overline{\nabla} T_{\rho}1_{\Omega_{i}}(x),X(x)\rangle \langle X(x),N(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad +\int_{\partial^{*}\Omega_{i}} T_{\rho}1_{\Omega_{i}}(x)\Big(\mathrm{div}(X(x))-\langle X(x),x\rangle\Big)\langle X(x),N(x)\rangle\gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$
$$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\int_{\mathbb{R}^{n+1}} \int_{\mathbb{R}^{n+1}} 1_{\Omega_{i}^{(s)}}(y)G(x,y) 1_{\Omega_{i}^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad =\int_{\partial^{*}\Omega_{i}}\int_{\partial^{*}\Omega_{i}}G(x,y)\langle X(x),N(x)\rangle \langle X(y),N(y)\rangle \,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad +\int_{\partial^{*}\Omega_{i}}\langle\overline{\nabla} T_{\rho}1_{\Omega_{i}}(x),X(x)\rangle \langle X(x),N(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad +\int_{\partial^{*}\Omega_{i}} T_{\rho}1_{\Omega_{i}}(x)\Big(\mathrm{div}(X(x))-\langle X(x),x\rangle\Big)\langle X(x),N(x)\rangle\gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$Summing over ![]() $1\leq i\leq m$ and using
$1\leq i\leq m$ and using ![]() $N_{ij}=-N_{ji}$ completes the proof.
$N_{ij}=-N_{ji}$ completes the proof.
Below, we need the following combinatorial lemma, the case ![]() $m=3$ being treated in [Reference Hutchings, Morgan, Ritoré and RosHMRR02, Proposition 3.3].
$m=3$ being treated in [Reference Hutchings, Morgan, Ritoré and RosHMRR02, Proposition 3.3].
Lemma 4.7 [Reference HeilmanHei19, Lemma 4.6]
Let ![]() $m\geq 3$. Let
$m\geq 3$. Let
 $$ \begin{align*}D_{1}\colon= \{(x_{ij})_{1\leq i\neq j\leq m}\in\mathbb{R}^{\binom{m}{2}}\colon \forall\,1\leq i\neq j\leq m,\quad x_{ij} =-x_{ji},\,\sum_{j\in\{1,\ldots,m\}\colon j\neq i}x_{ij}=0\}.\end{align*} $$
$$ \begin{align*}D_{1}\colon= \{(x_{ij})_{1\leq i\neq j\leq m}\in\mathbb{R}^{\binom{m}{2}}\colon \forall\,1\leq i\neq j\leq m,\quad x_{ij} =-x_{ji},\,\sum_{j\in\{1,\ldots,m\}\colon j\neq i}x_{ij}=0\}.\end{align*} $$ $$ \begin{align*} D_{2}\colon= \{(x_{ij})_{1\leq i\neq j\leq m}\in\mathbb{R}^{\binom{m}{2}} &\colon \forall\,1\leq i\neq j\leq m,\quad x_{ij}=-x_{ji},\\ &\forall\,1\leq i<j<k\leq m\quad x_{ij}+x_{jk}+x_{ki}=0\}. \end{align*} $$
$$ \begin{align*} D_{2}\colon= \{(x_{ij})_{1\leq i\neq j\leq m}\in\mathbb{R}^{\binom{m}{2}} &\colon \forall\,1\leq i\neq j\leq m,\quad x_{ij}=-x_{ji},\\ &\forall\,1\leq i<j<k\leq m\quad x_{ij}+x_{jk}+x_{ki}=0\}. \end{align*} $$Let ![]() $x\in D_{1}$ and let
$x\in D_{1}$ and let ![]() $y\in D_{2}$. Then
$y\in D_{2}$. Then ![]() $\sum _{1\leq i<j\leq m}x_{ij}y_{ij}=0$.
$\sum _{1\leq i<j\leq m}x_{ij}y_{ij}=0$.
Proof. ![]() $D_{1}$ is defined to be perpendicular to vectors in
$D_{1}$ is defined to be perpendicular to vectors in ![]() $D_{2}$ and vice versa. That is,
$D_{2}$ and vice versa. That is, ![]() $D_{1}$ and
$D_{1}$ and ![]() $D_{2}$ are orthogonal complements of each other, and in terms of vector spaces,
$D_{2}$ are orthogonal complements of each other, and in terms of vector spaces, ![]() $D_{1}\oplus D_{2}=\mathbb {R}^{\binom {m}{2}}$. Consequently, the inner product of any
$D_{1}\oplus D_{2}=\mathbb {R}^{\binom {m}{2}}$. Consequently, the inner product of any ![]() $x\in D_{1}$ and
$x\in D_{1}$ and ![]() $y\in D_{2}$ is zero.
$y\in D_{2}$ is zero.
Lemma 4.8 Volume-Preserving Second Variation of Maximisers, Multiple Sets
Let ![]() $\Omega _{1},\ldots ,\Omega _{m}\subseteq \mathbb {R}^{n+1}$ be a partition of
$\Omega _{1},\ldots ,\Omega _{m}\subseteq \mathbb {R}^{n+1}$ be a partition of ![]() $\mathbb {R}^{n+1}$ into measurable sets such that
$\mathbb {R}^{n+1}$ into measurable sets such that ![]() $\partial \Omega _{i}$ is a locally finite union of
$\partial \Omega _{i}$ is a locally finite union of ![]() $C^{\infty }$ manifolds for all
$C^{\infty }$ manifolds for all ![]() $1\leq i\leq m$. Let
$1\leq i\leq m$. Let 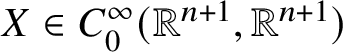 $X\in C_{0}^{\infty }(\mathbb {R}^{n+1},\mathbb {R}^{n+1})$. Let
$X\in C_{0}^{\infty }(\mathbb {R}^{n+1},\mathbb {R}^{n+1})$. Let  $\{\Omega _{i}^{(s)}\}_{s\in (-1,1)}$ be the corresponding variation of
$\{\Omega _{i}^{(s)}\}_{s\in (-1,1)}$ be the corresponding variation of ![]() $\Omega _{i}$ for all
$\Omega _{i}$ for all ![]() $1\leq i\leq m$. Denote
$1\leq i\leq m$. Denote ![]() $f_{ij}(x)\colon =\langle X(x),N_{ij}(x)\rangle $ for all
$f_{ij}(x)\colon =\langle X(x),N_{ij}(x)\rangle $ for all ![]() $x\in \Sigma _{ij}\colon = (\partial ^{*}\Omega _{i})\cap (\partial ^{*}\Omega _{j}) $. We let N denote the exterior pointing unit normal vector to
$x\in \Sigma _{ij}\colon = (\partial ^{*}\Omega _{i})\cap (\partial ^{*}\Omega _{j}) $. We let N denote the exterior pointing unit normal vector to ![]() $\partial ^{*}\Omega _{i}$ for any
$\partial ^{*}\Omega _{i}$ for any ![]() $1\leq i\leq m$. Then
$1\leq i\leq m$. Then
 $$ \begin{align} \begin{aligned} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}} \int_{\mathbb{R}^{n+1}} 1_{\Omega_{i}^{(s)}}(y)G(x,y) 1_{\Omega_{i}^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad\qquad = \sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}}\Big[\Big(\int_{\partial^{*}\Omega_{i}}-\int_{\partial^{*}\Omega_{j}}\Big)G(x,y)\langle X(y),N(y)\rangle \,\mathrm{d} y\Big] f_{ij}(x) \,\mathrm{d} x\\ &\qquad\qquad\qquad\qquad -\int_{\Sigma_{ij}}\|\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|(f_{ij}(x))^{2} \gamma_{n+1}(x)\,\mathrm{d} x. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}} \int_{\mathbb{R}^{n+1}} 1_{\Omega_{i}^{(s)}}(y)G(x,y) 1_{\Omega_{i}^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad\qquad = \sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}}\Big[\Big(\int_{\partial^{*}\Omega_{i}}-\int_{\partial^{*}\Omega_{j}}\Big)G(x,y)\langle X(y),N(y)\rangle \,\mathrm{d} y\Big] f_{ij}(x) \,\mathrm{d} x\\ &\qquad\qquad\qquad\qquad -\int_{\Sigma_{ij}}\|\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|(f_{ij}(x))^{2} \gamma_{n+1}(x)\,\mathrm{d} x. \end{aligned} \end{align} $$Also,
 $$ \begin{align} \overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)=-N_{ij}(x)\|\overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|,\qquad\forall\,x\in\Sigma_{ij}. \end{align} $$
$$ \begin{align} \overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)=-N_{ij}(x)\|\overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|,\qquad\forall\,x\in\Sigma_{ij}. \end{align} $$Moreover,  $\|\overline {\nabla } T_{\rho }(1_{\Omega _{i}}-1_{\Omega _{j}})(x)\|>0$ for all
$\|\overline {\nabla } T_{\rho }(1_{\Omega _{i}}-1_{\Omega _{j}})(x)\|>0$ for all ![]() $x\in \Sigma _{ij}$, except on a set of Hausdorff dimension at most
$x\in \Sigma _{ij}$, except on a set of Hausdorff dimension at most ![]() $n-1$.
$n-1$.
Proof. From Lemma 3.2, there exist constants ![]() $(c_{ij})_{1\leq i<j\leq m}$ such that
$(c_{ij})_{1\leq i<j\leq m}$ such that ![]() $T_{\rho }(1_{\Omega _{i}}-1_{\Omega _{j}})(x)=c_{ij}$ for all
$T_{\rho }(1_{\Omega _{i}}-1_{\Omega _{j}})(x)=c_{ij}$ for all ![]() $1\leq i<j\leq m$, for all
$1\leq i<j\leq m$, for all ![]() $x\in \Sigma _{ij}$. So, from Lemma 4.6,
$x\in \Sigma _{ij}$. So, from Lemma 4.6,
 $$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}} \int_{\mathbb{R}^{n+1}} 1_{\Omega_{i}^{(s)}}(y)G(x,y) 1_{\Omega_{i}^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad=\sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}}\Big[\Big(\int_{\partial^{*}\Omega_{i}}-\int_{\partial^{*}\Omega_{j}}\Big)G(x,y)\langle X(y),N(y)\rangle \,\mathrm{d} y\Big] \langle X(x),N_{ij}(x)\rangle \,\mathrm{d} x\\ &\qquad\qquad\qquad +\int_{\Sigma_{ij}}\langle\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x),X(x)\rangle \langle X(x),N_{ij}(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad\qquad + c_{ij}\int_{\Sigma_{ij}} \Big(\mathrm{div}(X(x))-\langle X(x),x\rangle\Big)\langle X(x),N_{ij}(x)\rangle\gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$
$$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}} \int_{\mathbb{R}^{n+1}} 1_{\Omega_{i}^{(s)}}(y)G(x,y) 1_{\Omega_{i}^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad=\sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}}\Big[\Big(\int_{\partial^{*}\Omega_{i}}-\int_{\partial^{*}\Omega_{j}}\Big)G(x,y)\langle X(y),N(y)\rangle \,\mathrm{d} y\Big] \langle X(x),N_{ij}(x)\rangle \,\mathrm{d} x\\ &\qquad\qquad\qquad +\int_{\Sigma_{ij}}\langle\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x),X(x)\rangle \langle X(x),N_{ij}(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad\qquad + c_{ij}\int_{\Sigma_{ij}} \Big(\mathrm{div}(X(x))-\langle X(x),x\rangle\Big)\langle X(x),N_{ij}(x)\rangle\gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$The last term then vanishes by Lemma 4.7. That is,
 $$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}} \int_{\mathbb{R}^{n+1}} 1_{\Omega_{i}^{(s)}}(y)G(x,y) 1_{\Omega_{i}^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad =\sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}}\Big[\Big(\int_{\partial^{*}\Omega_{i}}-\int_{\partial^{*}\Omega_{j}}\Big)G(x,y)\langle X(y),N(y)\rangle \,\mathrm{d} y\Big] \langle X(x),N_{ij}(x)\rangle \,\mathrm{d} x\\ &\qquad\qquad\qquad +\int_{\Sigma_{ij}}\langle\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x),X(x)\rangle \langle X(x),N_{ij}(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$
$$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}} \int_{\mathbb{R}^{n+1}} 1_{\Omega_{i}^{(s)}}(y)G(x,y) 1_{\Omega_{i}^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad =\sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}}\Big[\Big(\int_{\partial^{*}\Omega_{i}}-\int_{\partial^{*}\Omega_{j}}\Big)G(x,y)\langle X(y),N(y)\rangle \,\mathrm{d} y\Big] \langle X(x),N_{ij}(x)\rangle \,\mathrm{d} x\\ &\qquad\qquad\qquad +\int_{\Sigma_{ij}}\langle\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x),X(x)\rangle \langle X(x),N_{ij}(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$Meanwhile, if ![]() $1\leq i<j\leq m$ is fixed, it follows from Lemma 3.2 that
$1\leq i<j\leq m$ is fixed, it follows from Lemma 3.2 that
 $$ \begin{align} \overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)= \pm N_{ij}(x)\|\overline{\nabla }T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|,\qquad\forall\,x\in\Sigma_{ij}. \end{align} $$
$$ \begin{align} \overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)= \pm N_{ij}(x)\|\overline{\nabla }T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|,\qquad\forall\,x\in\Sigma_{ij}. \end{align} $$In fact, we must have a negative sign in (29); otherwise, we could find a vector field X supported near ![]() $x\in \Sigma _{ij}$ such that (25) has a positive sign, and then because G is a positive semidefinite function by Lemma 4.3, we would have
$x\in \Sigma _{ij}$ such that (25) has a positive sign, and then because G is a positive semidefinite function by Lemma 4.3, we would have
 $$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}} \int_{\mathbb{R}^{n+1}} 1_{\Omega_{i}^{(s)}}(y)G(x,y) 1_{\Omega_{i}^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad\geq\int_{\Sigma_{ij}}\langle\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x),X(x)\rangle \langle X(x),N(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x>0, \end{align*} $$
$$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}} \int_{\mathbb{R}^{n+1}} 1_{\Omega_{i}^{(s)}}(y)G(x,y) 1_{\Omega_{i}^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad\geq\int_{\Sigma_{ij}}\langle\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x),X(x)\rangle \langle X(x),N(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x>0, \end{align*} $$a contradiction. In summary,
 $$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}} \int_{\mathbb{R}^{n+1}} 1_{\Omega_{i}^{(s)}}(y)G(x,y) 1_{\Omega_{i}^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad\qquad =\sum_{1\leq i<j\leq m}\int_{\partial\Sigma_{ij}}\Big[\Big(\int_{\partial\Omega_{i}}-\int_{\partial\Omega_{j}}\Big)G(x,y)\langle X(y),N_{ij}(y)\rangle \,\mathrm{d} y\Big] \langle X(x),N_{ij}(x)\rangle \,\mathrm{d} x\\ &\qquad\qquad\qquad\qquad -\int_{\Sigma_{ij}}\|\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|\langle X(x),N_{ij}(x)\rangle^{2} \gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$
$$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}} \int_{\mathbb{R}^{n+1}} 1_{\Omega_{i}^{(s)}}(y)G(x,y) 1_{\Omega_{i}^{(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad\qquad =\sum_{1\leq i<j\leq m}\int_{\partial\Sigma_{ij}}\Big[\Big(\int_{\partial\Omega_{i}}-\int_{\partial\Omega_{j}}\Big)G(x,y)\langle X(y),N_{ij}(y)\rangle \,\mathrm{d} y\Big] \langle X(x),N_{ij}(x)\rangle \,\mathrm{d} x\\ &\qquad\qquad\qquad\qquad -\int_{\Sigma_{ij}}\|\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|\langle X(x),N_{ij}(x)\rangle^{2} \gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$5 Almost Eigenfunctions of the Second Variation
For didactic purposes, we first consider the case ![]() $m=2$, and we then later consider the case
$m=2$, and we then later consider the case ![]() $m>2$.
$m>2$.
5.1 Two Sets
Let ![]() $\Sigma \colon =\partial ^{*}\Omega $. For any bounded measurable
$\Sigma \colon =\partial ^{*}\Omega $. For any bounded measurable ![]() $f\colon \Sigma \to \mathbb {R}$, define the following function (if it exists):
$f\colon \Sigma \to \mathbb {R}$, define the following function (if it exists):
 $$ \begin{align} S(f)(x)\colon= (1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\int_{\Sigma}f(y)e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y,\qquad\forall\,x\in\Sigma. \end{align} $$
$$ \begin{align} S(f)(x)\colon= (1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\int_{\Sigma}f(y)e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y,\qquad\forall\,x\in\Sigma. \end{align} $$Lemma 5.1 Key Lemma,  $m=2$, Translations as Almost Eigenfunctions
$m=2$, Translations as Almost Eigenfunctions
Let ![]() $\Omega ,\Omega ^{c}$ maximise Problem 1.5 for
$\Omega ,\Omega ^{c}$ maximise Problem 1.5 for ![]() $m=2$. Let
$m=2$. Let ![]() $v\in \mathbb {R}^{n+1}$. Then
$v\in \mathbb {R}^{n+1}$. Then
 $$ \begin{align*}S(\langle v,N\rangle)(x)=\langle v,N(x)\rangle\frac{1}{\rho}\|\overline{\nabla} T_{\rho}1_{\Omega}(x)\|,\qquad\forall\,x\in\Sigma.\end{align*} $$
$$ \begin{align*}S(\langle v,N\rangle)(x)=\langle v,N(x)\rangle\frac{1}{\rho}\|\overline{\nabla} T_{\rho}1_{\Omega}(x)\|,\qquad\forall\,x\in\Sigma.\end{align*} $$Proof. Because ![]() $T_{\rho }1_{\Omega }(x)$ is constant for all
$T_{\rho }1_{\Omega }(x)$ is constant for all ![]() $x\in \partial \Omega $ by Lemma 3.2,
$x\in \partial \Omega $ by Lemma 3.2,  $\overline {\nabla } T_{\rho }1_{\Omega }(x)$ is parallel to
$\overline {\nabla } T_{\rho }1_{\Omega }(x)$ is parallel to ![]() $N(x)$ for all
$N(x)$ for all ![]() $x\in \partial \Omega $. That is, (24) holds; that is,
$x\in \partial \Omega $. That is, (24) holds; that is,
 $$ \begin{align} \overline{\nabla} T_{\rho}1_{\Omega}(x)=-N(x)\|\overline{\nabla} T_{\rho}1_{\Omega}(x)\|,\qquad\forall\,x\in\Sigma. \end{align} $$
$$ \begin{align} \overline{\nabla} T_{\rho}1_{\Omega}(x)=-N(x)\|\overline{\nabla} T_{\rho}1_{\Omega}(x)\|,\qquad\forall\,x\in\Sigma. \end{align} $$From Definition 3, and then using the divergence theorem,
 $$ \begin{align} \begin{aligned} \langle v,\overline{\nabla} T_{\rho}1_{\Omega}(x)\rangle &=(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\Big\langle v,\int_{\Omega} \overline{\nabla}_{x}e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y\Big\rangle\\ &=(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\frac{\rho}{1-\rho^{2}}\int_{\Omega} \langle v,\,y-\rho x\rangle e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y\\ &=-(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\rho\int_{\Omega} \mathrm{div}_{y}\Big(ve^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\Big)\,\mathrm{d} y\\ &=-(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\rho\int_{\Sigma}\langle v,N(y)\rangle e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y\\ &\stackrel{(30)}{=}-\rho\, S(\langle v,N\rangle)(x). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \langle v,\overline{\nabla} T_{\rho}1_{\Omega}(x)\rangle &=(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\Big\langle v,\int_{\Omega} \overline{\nabla}_{x}e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y\Big\rangle\\ &=(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\frac{\rho}{1-\rho^{2}}\int_{\Omega} \langle v,\,y-\rho x\rangle e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y\\ &=-(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\rho\int_{\Omega} \mathrm{div}_{y}\Big(ve^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\Big)\,\mathrm{d} y\\ &=-(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\rho\int_{\Sigma}\langle v,N(y)\rangle e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y\\ &\stackrel{(30)}{=}-\rho\, S(\langle v,N\rangle)(x). \end{aligned} \end{align} $$Therefore,
 $$ \begin{align*}\langle v,N(x)\rangle\|\overline{\nabla} T_{\rho}1_{\Omega}(x)\| \stackrel{(31)}{=}-\langle v,\overline{\nabla} T_{\rho}1_{\Omega}(x)\rangle \stackrel{(32)}{=}\rho\, S(\langle v,N\rangle)(x). \end{align*} $$
$$ \begin{align*}\langle v,N(x)\rangle\|\overline{\nabla} T_{\rho}1_{\Omega}(x)\| \stackrel{(31)}{=}-\langle v,\overline{\nabla} T_{\rho}1_{\Omega}(x)\rangle \stackrel{(32)}{=}\rho\, S(\langle v,N\rangle)(x). \end{align*} $$Remark 5.2. To justify the use of the divergence theorem in (32), let ![]() $r>0$ and note that we can differentiate under the integral sign of
$r>0$ and note that we can differentiate under the integral sign of ![]() $T_{\rho }1_{\Omega \cap B(0,r)}(x)$ to get
$T_{\rho }1_{\Omega \cap B(0,r)}(x)$ to get
 $$ \begin{align} \begin{aligned} \overline{\nabla} T_{\rho}1_{\Omega\cap B(0,r)}(x) &=(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\Big\langle v,\int_{\Omega\cap B(0,r)} \overline{\nabla}_{x}e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y\Big\rangle\\ &=(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\frac{\rho}{1-\rho^{2}}\int_{\Omega\cap B(0,r)} \langle v,\,y-\rho x\rangle e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y\\ &=-(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\rho\int_{\Omega\cap B(0,r)} \mathrm{div}_{y}\Big(ve^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\Big)\,\mathrm{d} y\\ &=-(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\rho\int_{(\Sigma\cap B(0,r))\cup(\Omega\cap\partial B(0,r))}\langle v,N(y)\rangle e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \overline{\nabla} T_{\rho}1_{\Omega\cap B(0,r)}(x) &=(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\Big\langle v,\int_{\Omega\cap B(0,r)} \overline{\nabla}_{x}e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y\Big\rangle\\ &=(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\frac{\rho}{1-\rho^{2}}\int_{\Omega\cap B(0,r)} \langle v,\,y-\rho x\rangle e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y\\ &=-(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\rho\int_{\Omega\cap B(0,r)} \mathrm{div}_{y}\Big(ve^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\Big)\,\mathrm{d} y\\ &=-(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\rho\int_{(\Sigma\cap B(0,r))\cup(\Omega\cap\partial B(0,r))}\langle v,N(y)\rangle e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y. \end{aligned} \end{align} $$Fix ![]() $r'>0$. Fix
$r'>0$. Fix ![]() $x\in \mathbb {R}^{n+1}$ with
$x\in \mathbb {R}^{n+1}$ with ![]() $\left \|x\right \|<r'$. The last integral in (33) over
$\left \|x\right \|<r'$. The last integral in (33) over ![]() $\Omega \cap \partial B(0,r)$ goes to zero as
$\Omega \cap \partial B(0,r)$ goes to zero as ![]() $r\to \infty $ uniformly over all such
$r\to \infty $ uniformly over all such ![]() $\left \|x\right \|<r'$. Also,
$\left \|x\right \|<r'$. Also,  $\overline {\nabla } T_{\rho }1_{\Omega }(x)$ exists a priori for all
$\overline {\nabla } T_{\rho }1_{\Omega }(x)$ exists a priori for all ![]() $x\in \mathbb {R}^{n+1}$, and
$x\in \mathbb {R}^{n+1}$, and
 $$ \begin{align*} &\left\|\overline{\nabla} T_{\rho}1_{\Omega}(x)-\overline{\nabla} T_{\rho}1_{\Omega\cap B(0,r)}(x)\right\| \stackrel{(3)}{=}\frac{\rho}{\sqrt{1-\rho^{2}}}\left\|\int_{\mathbb{R}^{n+1}} y 1_{\Omega\cap B(0,r)^{c}}(x\rho+y\sqrt{1-\rho^{2}})\gamma_{n+1}(y)\,\mathrm{d} y\right\|\\ &\qquad\qquad\qquad \leq\frac{\rho}{\sqrt{1-\rho^{2}}}\sup_{w\in\mathbb{R}^{n+1}\colon\left\|w\right\|=1}\int_{\mathbb{R}^{n+1}} \left|\langle w,y\rangle\right| 1_{B(0,r)^{c}}(x\rho+y\sqrt{1-\rho^{2}})\gamma_{n+1}(y)\,\mathrm{d} y. \end{align*} $$
$$ \begin{align*} &\left\|\overline{\nabla} T_{\rho}1_{\Omega}(x)-\overline{\nabla} T_{\rho}1_{\Omega\cap B(0,r)}(x)\right\| \stackrel{(3)}{=}\frac{\rho}{\sqrt{1-\rho^{2}}}\left\|\int_{\mathbb{R}^{n+1}} y 1_{\Omega\cap B(0,r)^{c}}(x\rho+y\sqrt{1-\rho^{2}})\gamma_{n+1}(y)\,\mathrm{d} y\right\|\\ &\qquad\qquad\qquad \leq\frac{\rho}{\sqrt{1-\rho^{2}}}\sup_{w\in\mathbb{R}^{n+1}\colon\left\|w\right\|=1}\int_{\mathbb{R}^{n+1}} \left|\langle w,y\rangle\right| 1_{B(0,r)^{c}}(x\rho+y\sqrt{1-\rho^{2}})\gamma_{n+1}(y)\,\mathrm{d} y. \end{align*} $$And the last integral goes to zero as ![]() $r\to \infty $, uniformly over all
$r\to \infty $, uniformly over all ![]() $\left \|x\right \|<r'$.
$\left \|x\right \|<r'$.
Lemma 5.3 Second Variation of Translations
Let ![]() $v\in \mathbb {R}^{n+1}$. Let
$v\in \mathbb {R}^{n+1}$. Let ![]() $\Omega ,\Omega ^{c}$ maximise Problem 1.5 for
$\Omega ,\Omega ^{c}$ maximise Problem 1.5 for ![]() $m=2$. Let
$m=2$. Let  $\{\Omega ^{(s)}\}_{s\in (-1,1)}$ be the variation of
$\{\Omega ^{(s)}\}_{s\in (-1,1)}$ be the variation of ![]() $\Omega $ corresponding to the constant vector field
$\Omega $ corresponding to the constant vector field ![]() $X\colon = v$. Assume that
$X\colon = v$. Assume that
 $$ \begin{align*}\int_{\Sigma}\langle v,N(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x=0.\end{align*} $$
$$ \begin{align*}\int_{\Sigma}\langle v,N(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x=0.\end{align*} $$Then
 $$ \begin{align*}\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\int_{\mathbb{R}^{n+1}}1_{\Omega^{(s)}}(x)T_{\rho}1_{\Omega^{(s)}}(x)\gamma_{n+1}(x)\,\mathrm{d} x =\Big(\frac{1}{\rho}-1\Big)\int_{\Sigma}\|\overline{\nabla}T_{\rho}1_{\Omega}(x)\|\langle v,N(x)\rangle^{2}\gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$
$$ \begin{align*}\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\int_{\mathbb{R}^{n+1}}1_{\Omega^{(s)}}(x)T_{\rho}1_{\Omega^{(s)}}(x)\gamma_{n+1}(x)\,\mathrm{d} x =\Big(\frac{1}{\rho}-1\Big)\int_{\Sigma}\|\overline{\nabla}T_{\rho}1_{\Omega}(x)\|\langle v,N(x)\rangle^{2}\gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$Proof. Let ![]() $f(x)\colon =\langle v,N(x)\rangle $ for all
$f(x)\colon =\langle v,N(x)\rangle $ for all ![]() $x\in \Sigma $. From Lemma 4.5,
$x\in \Sigma $. From Lemma 4.5,
 $$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\int_{\mathbb{R}^{n+1}}1_{\Omega^{(s)}}(x)T_{\rho}1_{\Omega^{(s)}}(x)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad\qquad =\int_{\Sigma} \Big(S(f)(x)-\|\overline{\nabla}T_{\rho}1_{\Omega}(x)\| f(x)\Big)f(x)\gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$
$$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\int_{\mathbb{R}^{n+1}}1_{\Omega^{(s)}}(x)T_{\rho}1_{\Omega^{(s)}}(x)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad\qquad =\int_{\Sigma} \Big(S(f)(x)-\|\overline{\nabla}T_{\rho}1_{\Omega}(x)\| f(x)\Big)f(x)\gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$Applying Lemma 5.1,  $S(f)(x)=f(x)\frac {1}{\rho }\|\overline {\nabla }T_{\rho }1_{\Omega }(x)\| \ \forall \ x\in \Sigma $, proving the lemma. Note also that
$S(f)(x)=f(x)\frac {1}{\rho }\|\overline {\nabla }T_{\rho }1_{\Omega }(x)\| \ \forall \ x\in \Sigma $, proving the lemma. Note also that  $\int _{\Sigma }\|\overline {\nabla }T_{\rho }1_{\Omega }(x)\|\langle v,N(x)\rangle ^{2}\gamma _{n+1}(x)\,\mathrm {d} x$ is finite priori by the divergence theorem and (24):
$\int _{\Sigma }\|\overline {\nabla }T_{\rho }1_{\Omega }(x)\|\langle v,N(x)\rangle ^{2}\gamma _{n+1}(x)\,\mathrm {d} x$ is finite priori by the divergence theorem and (24):
 $$ \begin{align*} \infty&>\left|\int_{\Omega}\Big\langle v,-x+\nabla\langle v,\overline{\nabla}T_{\rho}1_{\Omega}(x)\rangle\Big\rangle\gamma_{n+1}(x)\,\mathrm{d} x\right| =\left|\int_{\Omega}\mathrm{div}\Big(v\langle v,\overline{\nabla}T_{\rho}1_{\Omega}(x)\rangle\gamma_{n+1}(x)\Big)\,\mathrm{d} x\right|\\ &=\left|\int_{\Sigma}\langle v,N(x)\rangle\langle v,\overline{\nabla}T_{\rho}1_{\Omega}(x)\rangle\gamma_{n+1}(x)\,\mathrm{d} x\right| \stackrel{(24)}{=}\left|\int_{\Sigma}\|\overline{\nabla}T_{\rho}1_{\Omega}(x)\|\langle v,N(x)\rangle^{2}\gamma_{n+1}(x)\,\mathrm{d} x\right|. \end{align*} $$
$$ \begin{align*} \infty&>\left|\int_{\Omega}\Big\langle v,-x+\nabla\langle v,\overline{\nabla}T_{\rho}1_{\Omega}(x)\rangle\Big\rangle\gamma_{n+1}(x)\,\mathrm{d} x\right| =\left|\int_{\Omega}\mathrm{div}\Big(v\langle v,\overline{\nabla}T_{\rho}1_{\Omega}(x)\rangle\gamma_{n+1}(x)\Big)\,\mathrm{d} x\right|\\ &=\left|\int_{\Sigma}\langle v,N(x)\rangle\langle v,\overline{\nabla}T_{\rho}1_{\Omega}(x)\rangle\gamma_{n+1}(x)\,\mathrm{d} x\right| \stackrel{(24)}{=}\left|\int_{\Sigma}\|\overline{\nabla}T_{\rho}1_{\Omega}(x)\|\langle v,N(x)\rangle^{2}\gamma_{n+1}(x)\,\mathrm{d} x\right|. \end{align*} $$5.2 More Than Two Sets
Let ![]() $v\in \mathbb {R}^{n+1}$ and denote
$v\in \mathbb {R}^{n+1}$ and denote ![]() $f_{ij}\colon =\langle v,N_{ij}\rangle $ for all
$f_{ij}\colon =\langle v,N_{ij}\rangle $ for all ![]() $1\leq i,j\leq m$. For simplicity of notation in the formulas below, if
$1\leq i,j\leq m$. For simplicity of notation in the formulas below, if ![]() $1\leq i\leq m$ and if a vector
$1\leq i\leq m$ and if a vector ![]() $N(x)$ appears inside an integral over
$N(x)$ appears inside an integral over ![]() $\partial \Omega _{i}$, then
$\partial \Omega _{i}$, then ![]() $N(x)$ denotes the unit exterior pointing normal vector to
$N(x)$ denotes the unit exterior pointing normal vector to ![]() $\Omega _{i}$ at
$\Omega _{i}$ at ![]() $x\in \partial ^{*}\Omega _{i}$. Similarly, for simplicity of notation, we denote
$x\in \partial ^{*}\Omega _{i}$. Similarly, for simplicity of notation, we denote ![]() $\langle v,N\rangle $ as the collection of functions
$\langle v,N\rangle $ as the collection of functions ![]() $(\langle v,N_{ij}\rangle )_{1\leq i<j\leq m}$. For any
$(\langle v,N_{ij}\rangle )_{1\leq i<j\leq m}$. For any ![]() $1\leq i<j\leq m$, define
$1\leq i<j\leq m$, define
 $$ \begin{align} S_{ij}(\langle v,N\rangle)(x)\colon= (1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\Big(\int_{\partial\Omega_{i}}-\int_{\partial\Omega_{j}}\Big)\langle v,N(y)\rangle e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y,\,\forall\,x\in\Sigma_{ij}. \end{align} $$
$$ \begin{align} S_{ij}(\langle v,N\rangle)(x)\colon= (1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\Big(\int_{\partial\Omega_{i}}-\int_{\partial\Omega_{j}}\Big)\langle v,N(y)\rangle e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y,\,\forall\,x\in\Sigma_{ij}. \end{align} $$Lemma 5.4. Key Lemma,  $m\geq 2$, Translations as Almost Eigenfunctions
$m\geq 2$, Translations as Almost Eigenfunctions
Let ![]() $\Omega _{1},\ldots ,\Omega _{m}$ maximise problem 1.5. Fix
$\Omega _{1},\ldots ,\Omega _{m}$ maximise problem 1.5. Fix ![]() $1\leq i<j\leq m$. Let
$1\leq i<j\leq m$. Let ![]() $v\in \mathbb {R}^{n+1}$. Then
$v\in \mathbb {R}^{n+1}$. Then
 $$ \begin{align*}S_{ij}(\langle v,N\rangle)(x)=\langle v,N_{ij}(x)\rangle\frac{1}{\rho}\|\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|,\qquad\forall\,x\in\Sigma_{ij}.\end{align*} $$
$$ \begin{align*}S_{ij}(\langle v,N\rangle)(x)=\langle v,N_{ij}(x)\rangle\frac{1}{\rho}\|\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|,\qquad\forall\,x\in\Sigma_{ij}.\end{align*} $$Proof. From Lemma 4.8 (i.e., (28)),
 $$ \begin{align} \overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)=-N_{ij}(x)\|\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|,\qquad\forall\,x\in\Sigma_{ij}. \end{align} $$
$$ \begin{align} \overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)=-N_{ij}(x)\|\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|,\qquad\forall\,x\in\Sigma_{ij}. \end{align} $$From Definition 3, and then using the divergence theorem,
 $$ \begin{align} \begin{aligned} \langle v,\overline{\nabla} T_{\rho}1_{\Omega_{i}}(x)\rangle &=(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\Big\langle v,\int_{\Omega_{i}} \overline{\nabla}e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y\Big\rangle\\ &=(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\frac{\rho}{1-\rho^{2}}\int_{\Omega_{i}} \langle v,\,y-\rho x\rangle e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y\\ &=-(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2})\rho\int_{\Omega_{i}} \mathrm{div}\Big(ve^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\Big)\,\mathrm{d} y\\ &=-(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\rho\int_{\partial^{*}\Omega_{i}}\langle v,N(y)\rangle e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \langle v,\overline{\nabla} T_{\rho}1_{\Omega_{i}}(x)\rangle &=(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\Big\langle v,\int_{\Omega_{i}} \overline{\nabla}e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y\Big\rangle\\ &=(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\frac{\rho}{1-\rho^{2}}\int_{\Omega_{i}} \langle v,\,y-\rho x\rangle e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y\\ &=-(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2})\rho\int_{\Omega_{i}} \mathrm{div}\Big(ve^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\Big)\,\mathrm{d} y\\ &=-(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\rho\int_{\partial^{*}\Omega_{i}}\langle v,N(y)\rangle e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y. \end{aligned} \end{align} $$The use of the divergence theorem is justified in Remark 5.2. Therefore,
 $$ \begin{align*} &\langle v,N_{ij}(x)\rangle\|\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\| \stackrel{(35)}{=}-\langle v,\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\rangle\\ &\qquad\stackrel{(36)}{=}(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\rho\Big(\int_{\partial^{*}\Omega_{i}}-\int_{\partial^{*}\Omega_{j}}\Big)\langle v,N(y)\rangle e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y\\ &\qquad\stackrel{(34)}{=}\rho\, S_{ij}(\langle v,N\rangle)(x). \end{align*} $$
$$ \begin{align*} &\langle v,N_{ij}(x)\rangle\|\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\| \stackrel{(35)}{=}-\langle v,\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\rangle\\ &\qquad\stackrel{(36)}{=}(1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\rho\Big(\int_{\partial^{*}\Omega_{i}}-\int_{\partial^{*}\Omega_{j}}\Big)\langle v,N(y)\rangle e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y\\ &\qquad\stackrel{(34)}{=}\rho\, S_{ij}(\langle v,N\rangle)(x). \end{align*} $$Lemma 5.5 Second Variation of Translations, Multiple Sets
Let ![]() $v\in \mathbb {R}^{n+1}$. Let
$v\in \mathbb {R}^{n+1}$. Let ![]() $\Omega _{1},\ldots ,\Omega _{m}$ maximise problem 1.5. For each
$\Omega _{1},\ldots ,\Omega _{m}$ maximise problem 1.5. For each ![]() $1\leq i\leq m$, let
$1\leq i\leq m$, let  $\{\Omega _{i}^{(s)}\}_{s\in (-1,1)}$ be the variation of
$\{\Omega _{i}^{(s)}\}_{s\in (-1,1)}$ be the variation of ![]() $\Omega _{i}$ corresponding to the constant vector field
$\Omega _{i}$ corresponding to the constant vector field ![]() $X\colon = v$. Assume that
$X\colon = v$. Assume that
 $$ \begin{align*}\int_{\partial\Omega_{i}}\langle v,N(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x=0,\qquad\forall\,1\leq i\leq m.\end{align*} $$
$$ \begin{align*}\int_{\partial\Omega_{i}}\langle v,N(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x=0,\qquad\forall\,1\leq i\leq m.\end{align*} $$Then
 $$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}}1_{\Omega_{i}^{(s)}}(x)T_{\rho}1_{\Omega_{i}^{(s)}}(x)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad\qquad=\Big(\frac{1}{\rho}-1\Big)\sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}}\|\overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|\langle v,N_{ij}(x)\rangle^{2}\gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$
$$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}}1_{\Omega_{i}^{(s)}}(x)T_{\rho}1_{\Omega_{i}^{(s)}}(x)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad\qquad=\Big(\frac{1}{\rho}-1\Big)\sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}}\|\overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|\langle v,N_{ij}(x)\rangle^{2}\gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$Proof. For any ![]() $1\leq i<j\leq m$, let
$1\leq i<j\leq m$, let ![]() $f_{ij}(x)\colon =\langle v,N_{ij}(x)\rangle $ for all
$f_{ij}(x)\colon =\langle v,N_{ij}(x)\rangle $ for all ![]() $x\in \Sigma $. From Lemma 4.5,
$x\in \Sigma $. From Lemma 4.5,
 $$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}}1_{\Omega^{(s)}}(x)T_{\rho}1_{\Omega^{(s)}}(x)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad=\sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}} \Big(S_{ij}(\langle v,N\rangle)(x)-\|\overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\| f_{ij}(x)\Big)f_{ij}(x)\gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$
$$ \begin{align*} &\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}}1_{\Omega^{(s)}}(x)T_{\rho}1_{\Omega^{(s)}}(x)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad=\sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}} \Big(S_{ij}(\langle v,N\rangle)(x)-\|\overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\| f_{ij}(x)\Big)f_{ij}(x)\gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$Applying Lemma 5.4,  $S_{ij}(\langle v,N\rangle )(x)=f_{ij}(x)\frac {1}{\rho }\|\overline {\nabla }T_{\rho }(1_{\Omega _{i}}-1_{\Omega _{j}})(x)\|$, proving the lemma. Note also that
$S_{ij}(\langle v,N\rangle )(x)=f_{ij}(x)\frac {1}{\rho }\|\overline {\nabla }T_{\rho }(1_{\Omega _{i}}-1_{\Omega _{j}})(x)\|$, proving the lemma. Note also that  $\sum _{1\leq i<j\leq m}\int _{\Sigma _{ij}}\|\overline {\nabla }T_{\rho }(1_{\Omega _{i}}-1_{\Omega _{j}})(x)\|\langle v,N_{ij}(x)\rangle ^{2}\gamma _{n+1}(x)\,\mathrm {d} x$ is finite priori by the divergence theorem because
$\sum _{1\leq i<j\leq m}\int _{\Sigma _{ij}}\|\overline {\nabla }T_{\rho }(1_{\Omega _{i}}-1_{\Omega _{j}})(x)\|\langle v,N_{ij}(x)\rangle ^{2}\gamma _{n+1}(x)\,\mathrm {d} x$ is finite priori by the divergence theorem because
 $$ \begin{align*} \infty&>\left|\int_{\Omega_{i}}\Big\langle v,-x+\nabla\langle v,\overline{\nabla}T_{\rho}1_{\Omega_{i}}(x)\rangle\Big\rangle\gamma_{n+1}(x)\,\mathrm{d} x\right| =\left|\int_{\Omega_{i}}\mathrm{div}\Big(v\langle v,\overline{\nabla}T_{\rho}1_{\Omega_{i}}(x)\rangle\gamma_{n+1}(x)\Big)\,\mathrm{d} x\right|\\ &=\left|\int_{\Omega_{i}}\mathrm{div}\Big(v\langle v,\overline{\nabla}T_{\rho}1_{\Omega_{i}}(x)\rangle\gamma_{n+1}(x)\Big)\,\mathrm{d} x\right| =\left|\int_{\partial^{*}\Omega_{i}}\langle v,\overline{\nabla}T_{\rho}(1_{\Omega_{i}})(x)\rangle\langle v,N(x)\rangle\gamma_{n+1}(x)\,\mathrm{d} x\right|. \end{align*} $$
$$ \begin{align*} \infty&>\left|\int_{\Omega_{i}}\Big\langle v,-x+\nabla\langle v,\overline{\nabla}T_{\rho}1_{\Omega_{i}}(x)\rangle\Big\rangle\gamma_{n+1}(x)\,\mathrm{d} x\right| =\left|\int_{\Omega_{i}}\mathrm{div}\Big(v\langle v,\overline{\nabla}T_{\rho}1_{\Omega_{i}}(x)\rangle\gamma_{n+1}(x)\Big)\,\mathrm{d} x\right|\\ &=\left|\int_{\Omega_{i}}\mathrm{div}\Big(v\langle v,\overline{\nabla}T_{\rho}1_{\Omega_{i}}(x)\rangle\gamma_{n+1}(x)\Big)\,\mathrm{d} x\right| =\left|\int_{\partial^{*}\Omega_{i}}\langle v,\overline{\nabla}T_{\rho}(1_{\Omega_{i}})(x)\rangle\langle v,N(x)\rangle\gamma_{n+1}(x)\,\mathrm{d} x\right|. \end{align*} $$Summing over ![]() $1\leq i\leq m$ then gives
$1\leq i\leq m$ then gives
 $$ \begin{align*} \infty>&\left|\sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}}\langle v,\overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\rangle\langle v,N_{ij}(x)\rangle\gamma_{n+1}(x)\,\mathrm{d} x.\right|\\ &\stackrel{(28)}{=}\left|\sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}}\|\overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|\langle v,N_{ij}(x)\rangle^{2}\gamma_{n+1}(x)\,\mathrm{d} x.\right|. \end{align*} $$
$$ \begin{align*} \infty>&\left|\sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}}\langle v,\overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\rangle\langle v,N_{ij}(x)\rangle\gamma_{n+1}(x)\,\mathrm{d} x.\right|\\ &\stackrel{(28)}{=}\left|\sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}}\|\overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|\langle v,N_{ij}(x)\rangle^{2}\gamma_{n+1}(x)\,\mathrm{d} x.\right|. \end{align*} $$6 Proof of the Main Structure Theorem
Proof of Theorem 1.9. Let ![]() $m\geq 2$. Let
$m\geq 2$. Let ![]() $0<\rho <1$. Fix
$0<\rho <1$. Fix ![]() $a_{1},\ldots ,a_{m}>0$ such that
$a_{1},\ldots ,a_{m}>0$ such that ![]() $\sum _{i=1}^{m}a_{i}=1$. Let
$\sum _{i=1}^{m}a_{i}=1$. Let ![]() $\Omega _{1},\ldots \Omega _{m}\subseteq \mathbb {R}^{n+1}$ be measurable sets that partition
$\Omega _{1},\ldots \Omega _{m}\subseteq \mathbb {R}^{n+1}$ be measurable sets that partition ![]() $\mathbb {R}^{n+1}$ such that
$\mathbb {R}^{n+1}$ such that ![]() $\gamma _{n+1}(\Omega _{i})=a_{i}$ for all
$\gamma _{n+1}(\Omega _{i})=a_{i}$ for all ![]() $1\leq i\leq m$ that maximise Problem 1.5. These sets exist by Lemma 2.3 and from Lemma 2.4 their boundaries are locally finite unions of
$1\leq i\leq m$ that maximise Problem 1.5. These sets exist by Lemma 2.3 and from Lemma 2.4 their boundaries are locally finite unions of ![]() $C^{\infty }\ n$-dimensional manifolds. Define
$C^{\infty }\ n$-dimensional manifolds. Define ![]() $\Sigma _{ij}\colon =(\partial ^{*}\Omega _{i})\cap (\partial ^{*}\Omega _{j})$ for all
$\Sigma _{ij}\colon =(\partial ^{*}\Omega _{i})\cap (\partial ^{*}\Omega _{j})$ for all ![]() $1\leq i<j\leq m$.
$1\leq i<j\leq m$.
By Lemma 3.2, for all ![]() $1\leq i<j\leq m$, there exists
$1\leq i<j\leq m$, there exists ![]() $c_{ij}\in \mathbb {R}$ such that
$c_{ij}\in \mathbb {R}$ such that
By this condition, the regularity Lemma 2.4 and the last part of Lemma 4.8,
 $$ \begin{align*}\overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)= -N_{ij}(x)\|\overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|,\qquad\forall\,x\in\Sigma_{ij}.\end{align*} $$
$$ \begin{align*}\overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)= -N_{ij}(x)\|\overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|,\qquad\forall\,x\in\Sigma_{ij}.\end{align*} $$Moreover, by the last part of Lemma 4.8, except for a set ![]() $\sigma _{ij}$ of Hausdorff dimension at most
$\sigma _{ij}$ of Hausdorff dimension at most ![]() $n-1$, we have
$n-1$, we have
 $$ \begin{align} \|\overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|>0,\qquad\forall\,x\in\Sigma_{ij}\setminus\sigma_{ij}. \end{align} $$
$$ \begin{align} \|\overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|>0,\qquad\forall\,x\in\Sigma_{ij}\setminus\sigma_{ij}. \end{align} $$ Fix ![]() $v\in \mathbb {R}^{n+1}$ and consider the variation of
$v\in \mathbb {R}^{n+1}$ and consider the variation of ![]() $\Omega _{1},\ldots ,\Omega _{m}$ induced by the constant vector field
$\Omega _{1},\ldots ,\Omega _{m}$ induced by the constant vector field ![]() $X\colon = v$. For all
$X\colon = v$. For all ![]() $1\leq i<j\leq m$, define
$1\leq i<j\leq m$, define ![]() $S_{ij}$ as in (34). Define
$S_{ij}$ as in (34). Define
 $$ \begin{align*}V\colon=\Big\{v\in\mathbb{R}^{n+1}\colon \sum_{j\in\{1,\ldots,m\}\setminus\{i\}}\int_{\Sigma_{ij}}\langle v,N_{ij}(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x=0,\qquad\forall\,1\leq i\leq m\Big\}. \end{align*} $$
$$ \begin{align*}V\colon=\Big\{v\in\mathbb{R}^{n+1}\colon \sum_{j\in\{1,\ldots,m\}\setminus\{i\}}\int_{\Sigma_{ij}}\langle v,N_{ij}(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x=0,\qquad\forall\,1\leq i\leq m\Big\}. \end{align*} $$From Lemma 5.5,
 $$ \begin{align*} v\in V\,\Longrightarrow&\,\,\,\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}}1_{\Omega_{i}^{(s)}}(x)T_{\rho}1_{\Omega_{i}^{(s)}}(x)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad=\Big(\frac{1}{\rho}-1\Big)\sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}}\|\overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|\langle v,N_{ij}(x)\rangle^{2}\gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$
$$ \begin{align*} v\in V\,\Longrightarrow&\,\,\,\frac{1}{2}\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}}1_{\Omega_{i}^{(s)}}(x)T_{\rho}1_{\Omega_{i}^{(s)}}(x)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad=\Big(\frac{1}{\rho}-1\Big)\sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}}\|\overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|\langle v,N_{ij}(x)\rangle^{2}\gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$Because ![]() $0<\rho <1$, (37) implies
$0<\rho <1$, (37) implies
The set V has dimension at least ![]() $n+2-m$, by the rank-nullity theorem, because V is the null space of the linear operator
$n+2-m$, by the rank-nullity theorem, because V is the null space of the linear operator ![]() $M\colon \mathbb {R}^{n+1}\to \mathbb {R}^{m}$ defined by
$M\colon \mathbb {R}^{n+1}\to \mathbb {R}^{m}$ defined by
 $$ \begin{align*}(M(v))_{i}\colon= \sum_{j\in\{1,\ldots,m\}\setminus\{i\}}\int_{\Sigma_{ij}}\langle v,N_{ij}(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x,\qquad\forall\,1\leq i\leq m \end{align*} $$
$$ \begin{align*}(M(v))_{i}\colon= \sum_{j\in\{1,\ldots,m\}\setminus\{i\}}\int_{\Sigma_{ij}}\langle v,N_{ij}(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x,\qquad\forall\,1\leq i\leq m \end{align*} $$and M has rank at most ![]() $m-1$ (because
$m-1$ (because ![]() $\sum _{i=1}^{m}(M(v))_{i}=0$ for all
$\sum _{i=1}^{m}(M(v))_{i}=0$ for all ![]() $v\in \mathbb {R}^{n+1}$). So, by (38), after rotating
$v\in \mathbb {R}^{n+1}$). So, by (38), after rotating ![]() $\Omega _{1},\ldots ,\Omega _{m}$, we conclude that there exist measurable
$\Omega _{1},\ldots ,\Omega _{m}$, we conclude that there exist measurable  $\Omega _{1}',\ldots ,\Omega _{m}'\subseteq \mathbb {R}^{m-1}$ such that
$\Omega _{1}',\ldots ,\Omega _{m}'\subseteq \mathbb {R}^{m-1}$ such that
 $$ \begin{align*}\Omega_{i}=\Omega_{i}'\times\mathbb{R}^{n+2-m},\qquad\forall\,1\leq i\leq m.\end{align*} $$
$$ \begin{align*}\Omega_{i}=\Omega_{i}'\times\mathbb{R}^{n+2-m},\qquad\forall\,1\leq i\leq m.\end{align*} $$7 The Case of Negative Correlation
In this section, we consider the case that ![]() $\rho <0$ in Problem 1.5. When
$\rho <0$ in Problem 1.5. When ![]() $\rho <0$ and
$\rho <0$ and ![]() $h\colon \mathbb {R}^{n+1}\to [-1,1]$ is measurable, quantity
$h\colon \mathbb {R}^{n+1}\to [-1,1]$ is measurable, quantity
 $$ \begin{align*} \int_{\mathbb{R}^{n+1}}h(x)T_{\rho}h(x)\gamma_{n+1}(x)\,\mathrm{d} x \end{align*} $$
$$ \begin{align*} \int_{\mathbb{R}^{n+1}}h(x)T_{\rho}h(x)\gamma_{n+1}(x)\,\mathrm{d} x \end{align*} $$could be negative, so a few parts of the above argument do not work, namely, the existence Lemma 2.3. We therefore replace the noise stability with a more general bilinear expression, guaranteeing existence of the corresponding problem. The remaining parts of the argument are essentially identical, mutatis mutandis. We indicate below where the arguments differ in the bilinear case.
When ![]() $\rho <0$, we look for a minimum of noise stability, rather than a maximum. Correspondingly, we expect that the plurality function minimises noise stability when
$\rho <0$, we look for a minimum of noise stability, rather than a maximum. Correspondingly, we expect that the plurality function minimises noise stability when ![]() $\rho <0$. If
$\rho <0$. If ![]() $\rho <0$, then (3) implies that
$\rho <0$, then (3) implies that
 $$ \begin{align*}\int_{\mathbb{R}^{n+1}}h(x)T_{\rho}h(x)\gamma_{n+1}(x)\,\mathrm{d} x =\int_{\mathbb{R}^{n+1}}h(x)T_{(-\rho)}h(-x)\gamma_{n+1}(x)\,\mathrm{d} x.\end{align*} $$
$$ \begin{align*}\int_{\mathbb{R}^{n+1}}h(x)T_{\rho}h(x)\gamma_{n+1}(x)\,\mathrm{d} x =\int_{\mathbb{R}^{n+1}}h(x)T_{(-\rho)}h(-x)\gamma_{n+1}(x)\,\mathrm{d} x.\end{align*} $$So, in order to understand the minimum of noise stability for negative correlations, it suffices to consider the following bilinear version of the standard simplex problem with positive correlation.
Problem 7.1 Standard Simplex Problem, Bilinear Version, Positive Correlation [Reference Isaksson and MosselIM12]
Let ![]() $m\geq 3$. Fix
$m\geq 3$. Fix ![]() $a_{1},\ldots ,a_{m}>0$ such that
$a_{1},\ldots ,a_{m}>0$ such that ![]() $\sum _{i=1}^{m}a_{i}=1$. Fix
$\sum _{i=1}^{m}a_{i}=1$. Fix ![]() $0<\rho <1$. Find measurable sets
$0<\rho <1$. Find measurable sets  $\Omega _{1},\ldots \Omega _{m},\Omega _{1}',\ldots \Omega _{m}'\subseteq \mathbb {R}^{n+1}$ with
$\Omega _{1},\ldots \Omega _{m},\Omega _{1}',\ldots \Omega _{m}'\subseteq \mathbb {R}^{n+1}$ with  $\cup _{i=1}^{m}\Omega _{i}=\cup _{i=1}^{m}\Omega _{i}'=\mathbb {R}^{n+1}$ and
$\cup _{i=1}^{m}\Omega _{i}=\cup _{i=1}^{m}\Omega _{i}'=\mathbb {R}^{n+1}$ and ![]() $\gamma _{n+1}(\Omega _{i})=\gamma _{n+1}(\Omega _{i}')=a_{i}$ for all
$\gamma _{n+1}(\Omega _{i})=\gamma _{n+1}(\Omega _{i}')=a_{i}$ for all ![]() $1\leq i\leq m$ that minimise
$1\leq i\leq m$ that minimise
 $$ \begin{align*}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}}1_{\Omega_{i}}(x)T_{\rho}1_{\Omega_{i}'}(x)\gamma_{n+1}(x)\,\mathrm{d} x,\end{align*} $$
$$ \begin{align*}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}}1_{\Omega_{i}}(x)T_{\rho}1_{\Omega_{i}'}(x)\gamma_{n+1}(x)\,\mathrm{d} x,\end{align*} $$subject to the above constraints.
Conjecture 7.2 Standard Simplex Conjecture, Bilinear Version, Positive Correlation [Reference Isaksson and MosselIM12]
Let 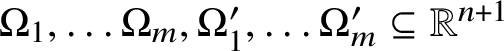 $\Omega _{1},\ldots \Omega _{m},\Omega _{1}',\ldots \Omega _{m}'\subseteq \mathbb {R}^{n+1}$ minimise Problem 1.5. Assume that
$\Omega _{1},\ldots \Omega _{m},\Omega _{1}',\ldots \Omega _{m}'\subseteq \mathbb {R}^{n+1}$ minimise Problem 1.5. Assume that ![]() $m-1\leq n+1$. Fix
$m-1\leq n+1$. Fix ![]() $0<\rho <1$. Let
$0<\rho <1$. Let ![]() $z_{1},\ldots ,z_{m}\in \mathbb {R}^{n+1}$ be the vertices of a regular simplex in
$z_{1},\ldots ,z_{m}\in \mathbb {R}^{n+1}$ be the vertices of a regular simplex in ![]() $\mathbb {R}^{n+1}$ centred at the origin. Then
$\mathbb {R}^{n+1}$ centred at the origin. Then ![]() $\exists \ w\in \mathbb {R}^{n+1}$ such that, for all
$\exists \ w\in \mathbb {R}^{n+1}$ such that, for all ![]() $1\leq i\leq m$,
$1\leq i\leq m$,
 $$ \begin{align*}\Omega_{i}=-\Omega_{i}'=w+\{x\in\mathbb{R}^{n+1}\colon\langle x,z_{i}\rangle=\max_{1\leq j\leq m}\langle x,z_{j}\rangle\}.\end{align*} $$
$$ \begin{align*}\Omega_{i}=-\Omega_{i}'=w+\{x\in\mathbb{R}^{n+1}\colon\langle x,z_{i}\rangle=\max_{1\leq j\leq m}\langle x,z_{j}\rangle\}.\end{align*} $$ In the case that ![]() $a_{i}=1/m$ for all
$a_{i}=1/m$ for all ![]() $1\leq i\leq m$, it is assumed that
$1\leq i\leq m$, it is assumed that ![]() $w=0$ in Conjecture 7.2.
$w=0$ in Conjecture 7.2.
Because we consider a bilinear version of noise stability in Problem 7.1, that existence of an optimiser is easier than in Problem 1.5.
Lemma 7.3 Existence of a Minimiser
Let ![]() $0<\rho <1$ and let
$0<\rho <1$ and let ![]() $m\geq 2$. Then there exist measurable sets
$m\geq 2$. Then there exist measurable sets ![]() $\Omega _{1},\ldots \Omega _{m},\Omega _{1}',\ldots \Omega _{m}'$ that minimise Problem 7.1.
$\Omega _{1},\ldots \Omega _{m},\Omega _{1}',\ldots \Omega _{m}'$ that minimise Problem 7.1.
Proof. Define ![]() $\Delta _{m}$ as in (6). Let
$\Delta _{m}$ as in (6). Let ![]() $f,g\colon \mathbb {R}^{n+1}\to \Delta _{m}$. The set
$f,g\colon \mathbb {R}^{n+1}\to \Delta _{m}$. The set ![]() $D_{0}\colon =\{f\colon \mathbb {R}^{n+1}\to \Delta _{m}\}$ is norm closed, bounded and convex; therefore, it is weakly compact and convex. Consider the function
$D_{0}\colon =\{f\colon \mathbb {R}^{n+1}\to \Delta _{m}\}$ is norm closed, bounded and convex; therefore, it is weakly compact and convex. Consider the function
 $$ \begin{align*} C(f,g)\colon=\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}}f_{i}(x)T_{\rho}g_{i}(x)\gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$
$$ \begin{align*} C(f,g)\colon=\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}}f_{i}(x)T_{\rho}g_{i}(x)\gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$This function is weakly continuous on ![]() $D_{0}\times D_{0}$, and
$D_{0}\times D_{0}$, and ![]() $D_{0}\times D_{0}$ is weakly compact, so there exists
$D_{0}\times D_{0}$ is weakly compact, so there exists ![]() $\widetilde {f},\widetilde {g}\in D_{0}$ such that
$\widetilde {f},\widetilde {g}\in D_{0}$ such that  $C(\widetilde {f},\widetilde {g})=\min _{f,g\in D}C(f,g)$. Because C is bilinear and
$C(\widetilde {f},\widetilde {g})=\min _{f,g\in D}C(f,g)$. Because C is bilinear and ![]() $D_{0}$ is convex, the minimum of C must be achieved at an extreme point of
$D_{0}$ is convex, the minimum of C must be achieved at an extreme point of ![]() $D_{0}\times D_{0}$. Let
$D_{0}\times D_{0}$. Let ![]() $e_{1},\ldots ,e_{m}$ denote the standard basis of
$e_{1},\ldots ,e_{m}$ denote the standard basis of ![]() $\mathbb {R}^{m}$, so that
$\mathbb {R}^{m}$, so that ![]() $f,g$ take their values in
$f,g$ take their values in ![]() $\{e_{1},\ldots ,e_{m}\}$. Then, for any
$\{e_{1},\ldots ,e_{m}\}$. Then, for any ![]() $1\leq i\leq m$, define
$1\leq i\leq m$, define ![]() $\Omega _{i}\colon =\{x\in \mathbb {R}^{n+1}\colon f(x)=e_{i}\}$ and
$\Omega _{i}\colon =\{x\in \mathbb {R}^{n+1}\colon f(x)=e_{i}\}$ and  $\Omega _{i}'\colon =\{x\in \mathbb {R}^{n+1}\colon g(x)=e_{i}\}$. Note that
$\Omega _{i}'\colon =\{x\in \mathbb {R}^{n+1}\colon g(x)=e_{i}\}$. Note that ![]() $f_{i}=1_{\Omega _{i}}$ and
$f_{i}=1_{\Omega _{i}}$ and ![]() $g_{i}=1_{\Omega _{i}'}$ for all
$g_{i}=1_{\Omega _{i}'}$ for all ![]() $1\leq i\leq m$.
$1\leq i\leq m$.
Lemma 7.4 Regularity of a Minimiser
Let  $\Omega _{1},\ldots ,\Omega _{m},\Omega _{1}',\ldots ,\Omega _{m}'\subseteq \mathbb {R}^{n+1}$ be the measurable sets minimising Problem 1.5, guaranteed to exist by Lemma 7.3. Then the sets
$\Omega _{1},\ldots ,\Omega _{m},\Omega _{1}',\ldots ,\Omega _{m}'\subseteq \mathbb {R}^{n+1}$ be the measurable sets minimising Problem 1.5, guaranteed to exist by Lemma 7.3. Then the sets ![]() $\Omega _{1},\ldots ,\Omega _{m},\Omega _{1}',\ldots ,\Omega _{m}'$ have locally finite surface area. Moreover, for all
$\Omega _{1},\ldots ,\Omega _{m},\Omega _{1}',\ldots ,\Omega _{m}'$ have locally finite surface area. Moreover, for all ![]() $1\leq i\leq m$ and for all
$1\leq i\leq m$ and for all ![]() $x\in \partial \Omega _{i}$, there exists a neighbourhood U of x such that
$x\in \partial \Omega _{i}$, there exists a neighbourhood U of x such that ![]() $U\cap \partial \Omega _{i}$ is a finite union of
$U\cap \partial \Omega _{i}$ is a finite union of ![]() $C^{\infty } \ n$-dimensional manifolds. The same holds for
$C^{\infty } \ n$-dimensional manifolds. The same holds for ![]() $\Omega _{1}',\ldots ,\Omega _{m}'$.
$\Omega _{1}',\ldots ,\Omega _{m}'$.
We denote  $\Sigma _{ij}\colon =(\partial ^{*}\Omega _{i})\cap (\partial ^{*}\Omega _{j}), \Sigma _{ij}'\colon =(\partial ^{*}\Omega _{i}')\cap (\partial ^{*}\Omega _{j}')$ for all
$\Sigma _{ij}\colon =(\partial ^{*}\Omega _{i})\cap (\partial ^{*}\Omega _{j}), \Sigma _{ij}'\colon =(\partial ^{*}\Omega _{i}')\cap (\partial ^{*}\Omega _{j}')$ for all ![]() $1\leq i<j\leq m$.
$1\leq i<j\leq m$.
Lemma 7.5 The First Variation for Minimisers
Suppose that  $\Omega _{1},\ldots ,\Omega _{m},\Omega _{1}',\ldots ,\Omega _{m}'\subseteq \mathbb {R}^{n+1}$ minimise Problem 7.1. Then for all
$\Omega _{1},\ldots ,\Omega _{m},\Omega _{1}',\ldots ,\Omega _{m}'\subseteq \mathbb {R}^{n+1}$ minimise Problem 7.1. Then for all ![]() $1\leq i<j\leq m$, there exists
$1\leq i<j\leq m$, there exists  $c_{ij},c_{ij}'\in \mathbb {R}$ such that
$c_{ij},c_{ij}'\in \mathbb {R}$ such that
 $$ \begin{align*}T_{\rho}(1_{\Omega_{i}'}-1_{\Omega_{j}'})(x)=c_{ij}',\qquad\forall\,x\in\Sigma_{ij}.\end{align*} $$
$$ \begin{align*}T_{\rho}(1_{\Omega_{i}'}-1_{\Omega_{j}'})(x)=c_{ij}',\qquad\forall\,x\in\Sigma_{ij}.\end{align*} $$ We denote ![]() $N_{ij}(x)$ as the unit exterior normal vector to
$N_{ij}(x)$ as the unit exterior normal vector to ![]() $\Sigma _{ij}$ for all
$\Sigma _{ij}$ for all ![]() $1\leq i<j\leq m$. Also, denote
$1\leq i<j\leq m$. Also, denote  $N_{ij}'(x)$ as the unit exterior normal vector to
$N_{ij}'(x)$ as the unit exterior normal vector to  $\Sigma _{ij}'$ for all
$\Sigma _{ij}'$ for all ![]() $1\leq i<j\leq m$. Let
$1\leq i<j\leq m$. Let  $\Omega _{1},\ldots ,\Omega _{m},\Omega _{1}',\ldots ,\Omega _{m}'\subseteq \mathbb {R}^{n+1}$ be a partition of
$\Omega _{1},\ldots ,\Omega _{m},\Omega _{1}',\ldots ,\Omega _{m}'\subseteq \mathbb {R}^{n+1}$ be a partition of ![]() $\mathbb {R}^{n+1}$ into measurable sets such that
$\mathbb {R}^{n+1}$ into measurable sets such that ![]() $\partial \Omega _{i},\partial \Omega _{i}'$ are a locally finite union of
$\partial \Omega _{i},\partial \Omega _{i}'$ are a locally finite union of ![]() $C^{\infty }$ manifolds for all
$C^{\infty }$ manifolds for all ![]() $1\leq i\leq m$. Let
$1\leq i\leq m$. Let  $X,X'\in C_{0}^{\infty }(\mathbb {R}^{n+1},\mathbb {R}^{n+1})$. Let
$X,X'\in C_{0}^{\infty }(\mathbb {R}^{n+1},\mathbb {R}^{n+1})$. Let  $\{\Omega _{i}^{(s)}\}_{s\in (-1,1)}$ be the variation of
$\{\Omega _{i}^{(s)}\}_{s\in (-1,1)}$ be the variation of ![]() $\Omega _{i}$ corresponding to X for all
$\Omega _{i}$ corresponding to X for all ![]() $1\leq i\leq m$. Let
$1\leq i\leq m$. Let  $\{\Omega _{i}^{'(s)}\}_{s\in (-1,1)}$ be the variation of
$\{\Omega _{i}^{'(s)}\}_{s\in (-1,1)}$ be the variation of ![]() $\Omega _{i}'$ corresponding to
$\Omega _{i}'$ corresponding to ![]() $X'$ for all
$X'$ for all ![]() $1\leq i\leq m$. Denote
$1\leq i\leq m$. Denote ![]() $f_{ij}(x)\colon =\langle X(x),N_{ij}(x)\rangle $ for all
$f_{ij}(x)\colon =\langle X(x),N_{ij}(x)\rangle $ for all ![]() $x\in \Sigma _{ij}$ and
$x\in \Sigma _{ij}$ and  $f_{ij}'(x)\colon =\langle X'(x),N_{ij}'(x)\rangle $ for all
$f_{ij}'(x)\colon =\langle X'(x),N_{ij}'(x)\rangle $ for all  $x\in \Sigma _{ij}'$. We let N denote the exterior pointing unit normal vector to
$x\in \Sigma _{ij}'$. We let N denote the exterior pointing unit normal vector to ![]() $\partial ^{*}\Omega _{i}$ for any
$\partial ^{*}\Omega _{i}$ for any ![]() $1\leq i\leq m$ and we let
$1\leq i\leq m$ and we let ![]() $N'$ denote the exterior pointing unit normal vector to
$N'$ denote the exterior pointing unit normal vector to ![]() $\partial ^{*}\Omega _{i}'$ for any
$\partial ^{*}\Omega _{i}'$ for any ![]() $1\leq i\leq m$.
$1\leq i\leq m$.
Lemma 7.6 Volume-Preserving Second Variation of Minimisers, Multiple Sets
Let  $\Omega _{1},\ldots ,\Omega _{m},\Omega _{1}',\ldots ,\Omega _{m}'\subseteq \mathbb {R}^{n+1}$ be two partitions of
$\Omega _{1},\ldots ,\Omega _{m},\Omega _{1}',\ldots ,\Omega _{m}'\subseteq \mathbb {R}^{n+1}$ be two partitions of ![]() $\mathbb {R}^{n+1}$ into measurable sets such that
$\mathbb {R}^{n+1}$ into measurable sets such that ![]() $\partial \Omega _{i},\partial \Omega _{i}'$ are a locally finite union of
$\partial \Omega _{i},\partial \Omega _{i}'$ are a locally finite union of ![]() $C^{\infty }$ manifolds for all
$C^{\infty }$ manifolds for all ![]() $1\leq i\leq m$. Then
$1\leq i\leq m$. Then
 $$ \begin{align} \begin{aligned} &\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}} \int_{\mathbb{R}^{n+1}} 1_{\Omega_{i}^{(s)}}(y)G(x,y) 1_{\Omega_{i}^{'(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad\qquad=\sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}'}\Big[\Big(\int_{\partial^{*}\Omega_{i}}-\int_{\partial^{*}\Omega_{j}}\Big)G(x,y)\langle X(y),N(y)\rangle \,\mathrm{d} y\Big] f_{ij}'(x) \,\mathrm{d} x\\ &\qquad\qquad\qquad\qquad +\sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}}\Big[\Big(\int_{\partial^{*}\Omega_{i}'}-\int_{\partial^{*}\Omega_{j}'}\Big)G(x,y)\langle X'(y),N'(y)\rangle \,\mathrm{d} y\Big] f_{ij}(x) \,\mathrm{d} x\\ &\qquad\qquad\qquad\qquad\qquad +\int_{\Sigma_{ij}'}\|\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|(f_{ij}'(x))^{2} \gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad\qquad\qquad\qquad +\int_{\Sigma_{ij}}\|\overline{\nabla} T_{\rho}(1_{\Omega_{i}'}-1_{\Omega_{j}'})(x)\|(f_{ij}(x))^{2} \gamma_{n+1}(x)\,\mathrm{d} x. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}} \int_{\mathbb{R}^{n+1}} 1_{\Omega_{i}^{(s)}}(y)G(x,y) 1_{\Omega_{i}^{'(s)}}(x)\,\mathrm{d} x\mathrm{d} y\\ &\qquad\qquad\qquad=\sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}'}\Big[\Big(\int_{\partial^{*}\Omega_{i}}-\int_{\partial^{*}\Omega_{j}}\Big)G(x,y)\langle X(y),N(y)\rangle \,\mathrm{d} y\Big] f_{ij}'(x) \,\mathrm{d} x\\ &\qquad\qquad\qquad\qquad +\sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}}\Big[\Big(\int_{\partial^{*}\Omega_{i}'}-\int_{\partial^{*}\Omega_{j}'}\Big)G(x,y)\langle X'(y),N'(y)\rangle \,\mathrm{d} y\Big] f_{ij}(x) \,\mathrm{d} x\\ &\qquad\qquad\qquad\qquad\qquad +\int_{\Sigma_{ij}'}\|\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|(f_{ij}'(x))^{2} \gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad\qquad\qquad\qquad +\int_{\Sigma_{ij}}\|\overline{\nabla} T_{\rho}(1_{\Omega_{i}'}-1_{\Omega_{j}'})(x)\|(f_{ij}(x))^{2} \gamma_{n+1}(x)\,\mathrm{d} x. \end{aligned} \end{align} $$Also,
 $$ \begin{align} \begin{aligned} \overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)&=N_{ij}'(x)\|\overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|,\qquad\forall\,x\in\Sigma_{ij}'.\\ \overline{\nabla}T_{\rho}(1_{\Omega_{i}'}-1_{\Omega_{j}'})(x)&=N_{ij}(x)\|\overline{\nabla}T_{\rho}(1_{\Omega_{i}'}-1_{\Omega_{j}'})(x)\|,\qquad\forall\,x\in\Sigma_{ij}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)&=N_{ij}'(x)\|\overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|,\qquad\forall\,x\in\Sigma_{ij}'.\\ \overline{\nabla}T_{\rho}(1_{\Omega_{i}'}-1_{\Omega_{j}'})(x)&=N_{ij}(x)\|\overline{\nabla}T_{\rho}(1_{\Omega_{i}'}-1_{\Omega_{j}'})(x)\|,\qquad\forall\,x\in\Sigma_{ij}. \end{aligned} \end{align} $$Moreover,  $\|\overline {\nabla } T_{\rho }(1_{\Omega _{i}}-1_{\Omega _{j}})(x)\|>0$ for all
$\|\overline {\nabla } T_{\rho }(1_{\Omega _{i}}-1_{\Omega _{j}})(x)\|>0$ for all  $x\in \Sigma _{ij}'$, except on a set of Hausdorff dimension at most
$x\in \Sigma _{ij}'$, except on a set of Hausdorff dimension at most ![]() $n-1$, and
$n-1$, and  $\|\overline {\nabla } T_{\rho }(1_{\Omega _{i}'}-1_{\Omega _{j}'})(x)\|>0$ for all
$\|\overline {\nabla } T_{\rho }(1_{\Omega _{i}'}-1_{\Omega _{j}'})(x)\|>0$ for all ![]() $x\in \Sigma _{ij}$, except on a set of Hausdorff dimension at most
$x\in \Sigma _{ij}$, except on a set of Hausdorff dimension at most ![]() $n-1$.
$n-1$.
Equation (40) and the last assertion require a slightly different argument than previously used. To see the last assertion, note that if there exists ![]() $1\leq i<j\leq m$ such that
$1\leq i<j\leq m$ such that  $\left \|\overline {\nabla } T_{\rho }(1_{\Omega _{i}}-1_{\Omega _{j}})(x)\right \|=0$ on an open set in
$\left \|\overline {\nabla } T_{\rho }(1_{\Omega _{i}}-1_{\Omega _{j}})(x)\right \|=0$ on an open set in  $\Sigma _{ij}'$, then choose
$\Sigma _{ij}'$, then choose ![]() $X'$ supported in this open set so that the third term of (39) is zero. Then, choose Y such that sum of the first two terms in (39) is negative. Then multiplying X by a small positive constant, and noting that the fourth term in (39) has quadratic dependence on X, we can create a negative second derivative of the noise stability, giving a contradiction. We can similarly justify the positive signs appearing in (40) (as opposed to the negative signs from (28)).
$X'$ supported in this open set so that the third term of (39) is zero. Then, choose Y such that sum of the first two terms in (39) is negative. Then multiplying X by a small positive constant, and noting that the fourth term in (39) has quadratic dependence on X, we can create a negative second derivative of the noise stability, giving a contradiction. We can similarly justify the positive signs appearing in (40) (as opposed to the negative signs from (28)).
Let ![]() $v\in \mathbb {R}^{n+1}$. For simplicity of notation, we denote
$v\in \mathbb {R}^{n+1}$. For simplicity of notation, we denote ![]() $\langle v,N\rangle $ as the collection of functions
$\langle v,N\rangle $ as the collection of functions ![]() $(\langle v,N_{ij}\rangle )_{1\leq i<j\leq m}$ and we denote
$(\langle v,N_{ij}\rangle )_{1\leq i<j\leq m}$ and we denote ![]() $\langle v,N'\rangle $ as the collection of functions
$\langle v,N'\rangle $ as the collection of functions  $(\langle v,N_{ij}'\rangle )_{1\leq i<j\leq m}$. For any
$(\langle v,N_{ij}'\rangle )_{1\leq i<j\leq m}$. For any ![]() $1\leq i<j\leq m$, define
$1\leq i<j\leq m$, define
 $$ \begin{align} \begin{aligned} S_{ij}(\langle v,N\rangle)(x) &\colon = (1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\Big(\int_{\partial\Omega_{i}}-\int_{\partial\Omega_{j}}\Big)\langle v,N(y)\rangle e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y, \,\forall\,x\in\Sigma_{ij'}\\ S_{ij}'(\langle v,N'\rangle)(x) &\colon = (1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\Big(\int_{\partial\Omega_{i}'}-\int_{\partial\Omega_{j}'}\Big)\langle v,N'(y)\rangle e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y \,\forall\,x\in\Sigma_{ij}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} S_{ij}(\langle v,N\rangle)(x) &\colon = (1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\Big(\int_{\partial\Omega_{i}}-\int_{\partial\Omega_{j}}\Big)\langle v,N(y)\rangle e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y, \,\forall\,x\in\Sigma_{ij'}\\ S_{ij}'(\langle v,N'\rangle)(x) &\colon = (1-\rho^{2})^{-(n+1)/2}(2\pi)^{-(n+1)/2}\Big(\int_{\partial\Omega_{i}'}-\int_{\partial\Omega_{j}'}\Big)\langle v,N'(y)\rangle e^{-\frac{\left\|y-\rho x\right\|^{2}}{2(1-\rho^{2})}}\,\mathrm{d} y \,\forall\,x\in\Sigma_{ij}. \end{aligned} \end{align} $$Lemma 7.7. Key Lemma,  $m\geq 2$, Translations as Almost Eigenfunctions
$m\geq 2$, Translations as Almost Eigenfunctions
Let  $\Omega _{1},\ldots , \Omega _{m}, \Omega _{1}',\ldots ,\Omega _{m}'\subseteq \mathbb {R}^{n+1}$ minimise problem 7.1. Fix
$\Omega _{1},\ldots , \Omega _{m}, \Omega _{1}',\ldots ,\Omega _{m}'\subseteq \mathbb {R}^{n+1}$ minimise problem 7.1. Fix ![]() $1\leq i<j\leq m$. Let
$1\leq i<j\leq m$. Let ![]() $v\in \mathbb {R}^{n+1}$. Then
$v\in \mathbb {R}^{n+1}$. Then
 $$ \begin{align*} S_{ij}(\langle v,N\rangle)(x) &=-\langle v,N_{ij}'(x)\rangle\frac{1}{\rho}\|\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|,\qquad\forall\,x\in\Sigma_{ij}'.\\ S_{ij}'(\langle v,N'\rangle)(x) &=-\langle v,N_{ij}(x)\rangle\frac{1}{\rho}\|\overline{\nabla} T_{\rho}(1_{\Omega_{i}'}-1_{\Omega_{j}'})(x)\|,\qquad\forall\,x\in\Sigma_{ij}. \end{align*} $$
$$ \begin{align*} S_{ij}(\langle v,N\rangle)(x) &=-\langle v,N_{ij}'(x)\rangle\frac{1}{\rho}\|\overline{\nabla} T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|,\qquad\forall\,x\in\Sigma_{ij}'.\\ S_{ij}'(\langle v,N'\rangle)(x) &=-\langle v,N_{ij}(x)\rangle\frac{1}{\rho}\|\overline{\nabla} T_{\rho}(1_{\Omega_{i}'}-1_{\Omega_{j}'})(x)\|,\qquad\forall\,x\in\Sigma_{ij}. \end{align*} $$When compared to Lemma 5.4, Lemma 7.7 has a negative sign on the right side of the equality, resulting from the positive sign in (40) (as opposed to the negative sign on the right side of (28)). Lemmas 7.6 and 7.7 then imply the following.
Lemma 7.8 Second Variation of Translations, Multiple Sets
Let ![]() $0<\rho <1$. Let
$0<\rho <1$. Let ![]() $v\in \mathbb {R}^{n+1}$. Let
$v\in \mathbb {R}^{n+1}$. Let ![]() $\Omega _{1},\ldots ,\Omega _{m}$ minimise Problem 1.5. For each
$\Omega _{1},\ldots ,\Omega _{m}$ minimise Problem 1.5. For each ![]() $1\leq i\leq m$, let
$1\leq i\leq m$, let  $\{\Omega _{i}^{(s)}\}_{s\in (-1,1)}$ be the variation of
$\{\Omega _{i}^{(s)}\}_{s\in (-1,1)}$ be the variation of ![]() $\Omega _{i}$ corresponding to the constant vector field
$\Omega _{i}$ corresponding to the constant vector field ![]() $X\colon = v$. Assume that
$X\colon = v$. Assume that
 $$ \begin{align*}\int_{\partial\Omega_{i}}\langle v,N(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x=\int_{\partial\Omega_{i}'}\langle v,N(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x=0,\qquad\forall\,1\leq i\leq m.\end{align*} $$
$$ \begin{align*}\int_{\partial\Omega_{i}}\langle v,N(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x=\int_{\partial\Omega_{i}'}\langle v,N(x)\rangle \gamma_{n+1}(x)\,\mathrm{d} x=0,\qquad\forall\,1\leq i\leq m.\end{align*} $$Then
 $$ \begin{align*} &\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}}1_{\Omega_{i}^{(s)}}(x)T_{\rho}1_{\Omega_{i}^{'(s)}}(x)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad\qquad =\Big(-\frac{1}{\rho}+1\Big)\sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}}\|\overline{\nabla}T_{\rho}(1_{\Omega_{i}'}-1_{\Omega_{j}'})(x)\|\langle v,N_{ij}(x)\rangle^{2}\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad\qquad\quad\,\, +\Big(-\frac{1}{\rho}+1\Big)\sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}'}\|\overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|\langle v,N_{ij}'(x)\rangle^{2}\gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$
$$ \begin{align*} &\frac{\mathrm{d}^{2}}{\mathrm{d} s^{2}}\Big|_{s=0}\sum_{i=1}^{m}\int_{\mathbb{R}^{n+1}}1_{\Omega_{i}^{(s)}}(x)T_{\rho}1_{\Omega_{i}^{'(s)}}(x)\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad\qquad =\Big(-\frac{1}{\rho}+1\Big)\sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}}\|\overline{\nabla}T_{\rho}(1_{\Omega_{i}'}-1_{\Omega_{j}'})(x)\|\langle v,N_{ij}(x)\rangle^{2}\gamma_{n+1}(x)\,\mathrm{d} x\\ &\qquad\qquad\qquad\quad\,\, +\Big(-\frac{1}{\rho}+1\Big)\sum_{1\leq i<j\leq m}\int_{\Sigma_{ij}'}\|\overline{\nabla}T_{\rho}(1_{\Omega_{i}}-1_{\Omega_{j}})(x)\|\langle v,N_{ij}'(x)\rangle^{2}\gamma_{n+1}(x)\,\mathrm{d} x. \end{align*} $$ Because ![]() $\rho \in (0,1)$,
$\rho \in (0,1)$,  $-\frac {1}{\rho }+1<0$. (The analogous inequality in Lemma 5.5 was
$-\frac {1}{\rho }+1<0$. (The analogous inequality in Lemma 5.5 was  $\frac {1}{\rho }-1>0$.) Repeating the argument of Theorem 1.9 then gives the following.
$\frac {1}{\rho }-1>0$.) Repeating the argument of Theorem 1.9 then gives the following.
Theorem 7.9 Main Structure Theorem/Dimension Reduction, Negative Correlation
Fix ![]() $0<\rho <1$. Let
$0<\rho <1$. Let ![]() $m\geq 2$ with
$m\geq 2$ with ![]() $2m\leq n+3$. Let
$2m\leq n+3$. Let  $\Omega _{1},\ldots \Omega _{m},\Omega _{1}',\ldots \Omega _{m}'\subseteq \mathbb {R}^{n+1}$ minimise Problem 7.1. Then, after rotating the sets
$\Omega _{1},\ldots \Omega _{m},\Omega _{1}',\ldots \Omega _{m}'\subseteq \mathbb {R}^{n+1}$ minimise Problem 7.1. Then, after rotating the sets ![]() $\Omega _{1},\ldots \Omega _{m},\Omega _{1}',\ldots \Omega _{m}'$ and applying Lebesgue measure zero changes to these sets, there exist measurable sets
$\Omega _{1},\ldots \Omega _{m},\Omega _{1}',\ldots \Omega _{m}'$ and applying Lebesgue measure zero changes to these sets, there exist measurable sets  $\Theta _{1},\ldots \Theta _{m},\Theta _{1}',\ldots \Theta _{m}'\subseteq \mathbb {R}^{2m-2}$ such that
$\Theta _{1},\ldots \Theta _{m},\Theta _{1}',\ldots \Theta _{m}'\subseteq \mathbb {R}^{2m-2}$ such that
 $$ \begin{align*}\Omega_{i}=\Theta_{i}\times\mathbb{R}^{n-2m+3},\,\,\Omega_{i}'=\Theta_{i}'\times\mathbb{R}^{n-2m+3}\qquad\forall\, 1\leq i\leq m.\end{align*} $$
$$ \begin{align*}\Omega_{i}=\Theta_{i}\times\mathbb{R}^{n-2m+3},\,\,\Omega_{i}'=\Theta_{i}'\times\mathbb{R}^{n-2m+3}\qquad\forall\, 1\leq i\leq m.\end{align*} $$Acknowledgements
SH is supported by NSF Grant CCF 1911216.
Conflicts of interest
None.