Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T12:14:02.057Z Has data issue: false hasContentIssue false
  • English
  • Français

TILTING THEORY FOR GORENSTEIN RINGS IN DIMENSION ONE

Part of: Theory of modules and ideals Homological methods

Published online by Cambridge University Press:  03 July 2020

RAGNAR-OLAF BUCHWEITZ ,
OSAMU IYAMA  and
KOTA YAMAURA
RAGNAR-OLAF BUCHWEITZ
Affiliation:
Department of Computer and Mathematical Sciences, University of Toronto Scarborough, Toronto, Ontario, CanadaM1C 1A4
OSAMU IYAMA
Affiliation:
Graduate School of Mathematics, Nagoya University, Furocho, Chikusaku, Nagoya464-8602, Japan; iyama@math.nagoya-u.ac.jp
KOTA YAMAURA
Affiliation:
Graduate Faculty of Interdisciplinary Research, Faculty of Engineering, University of Yamanashi, Takeda, Kofu400-8510, Japan; kyamaura@yamanashi.ac.jp

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In representation theory, commutative algebra and algebraic geometry, it is an important problem to understand when the triangulated category 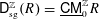$\mathsf{D}_{\operatorname{sg}}^{\mathbb{Z}}(R)=\text{}\underline{\mathsf{CM}}_{0}^{\mathbb{Z}}R$ admits a tilting (respectively, silting) object for a 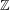$\mathbb{Z}$-graded commutative Gorenstein ring 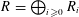$R=\bigoplus _{i\geqslant 0}R_{i}$. Here 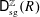$\mathsf{D}_{\operatorname{sg}}^{\mathbb{Z}}(R)$ is the singularity category, and 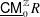$\text{}\underline{\mathsf{CM}}_{0}^{\mathbb{Z}}R$ is the stable category of 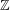$\mathbb{Z}$-graded Cohen–Macaulay (CM) 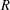$R$-modules, which are locally free at all nonmaximal prime ideals of 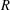$R$.

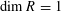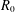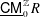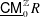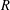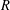In this paper, we give a complete answer to this problem in the case where $\dim R=1$ and $R_{0}$ is a field. We prove that $\text{}\underline{\mathsf{CM}}_{0}^{\mathbb{Z}}R$ always admits a silting object, and that $\text{}\underline{\mathsf{CM}}_{0}^{\mathbb{Z}}R$ admits a tilting object if and only if either $R$ is regular or the $a$-invariant of $R$ is nonnegative. Our silting/tilting object will be given explicitly. We also show that if 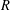$R$ is reduced and nonregular, then its $a$-invariant is nonnegative and the above tilting object gives a full strong exceptional collection in 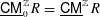$\text{}\underline{\mathsf{CM}}_{0}^{\mathbb{Z}}R=\text{}\underline{\mathsf{CM}}^{\mathbb{Z}}R$.

MSC classification

Primary: 13C14: Cohen-Macaulay modules
Secondary: 16E35: Derived categories
Type
Algebra
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e36
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Footnotes

†

The first author passed away on November 11, 2017.

References

Aihara, T. and Iyama, O., ‘Silting mutation in triangulated categories’, J. Lond. Math. Soc. 85(3) (2012), 633–668.CrossRefGoogle Scholar
Amiot, C., Iyama, O. and Reiten, I., ‘Stable categories of Cohen–Macaulay modules and cluster categories’, Amer. J. Math. 137(3) (2015), 813–857.CrossRefGoogle Scholar
Angeleri Hügel, L., Happel, D. and Krause, H., Handbook of Tilting Theory, London Mathematical Society Lecture Note Series, 332 (Cambridge University Press, Cambridge, 2007).CrossRefGoogle Scholar
Araya, T., ‘Exceptional sequences over graded Cohen–Macaulay rings’, Math. J. Okayama Univ. 41 (1999), 81–102 (2001).Google Scholar
Auslander, M., ‘Functors and morphisms determined by objects’, inRepresentation Theory of Algebras (Proc. Conf., Temple Univ., Philadelphia, PA, 1976), Lecture Notes in Pure and Applied Mathematics, 37 (Dekker, New York, 1978), 1–244.Google Scholar
Auslander, M. and Reiten, I., ‘Almost split sequences for Z-graded rings’, inSingularities, Representation of Algebras, and Vector Bundles (Lambrecht, 1985), Lecture Notes in Mathematics, 1273 (Springer, Berlin, 1987), 232–243.CrossRefGoogle Scholar
Auslander, M. and Reiten, I., ‘Cohen–Macaulay modules for graded Cohen–Macaulay rings and their completions’, inCommutative Algebra (Berkeley, CA, 1987), Mathematical Sciences Research Institute Publications, 15 (Springer, New York, 1989), 21–31.CrossRefGoogle Scholar
Beilinson, A. A., ‘Coherent sheaves on Pn and problems in linear algebra’, Funktsional. Anal. i Prilozhen. 12(3) (1978), 68–69.CrossRefGoogle Scholar
Bernstein, I. N., Gelfand, I. M. and Gelfand, S. I., ‘Algebraic vector bundles on Pn and problems of linear algebra’, Funktsional. Anal. i Prilozhen. 12(3) (1978), 66–67.Google Scholar
Bruns, W. and Herzog, J., Cohen–Macaulay Rings, Cambridge Studies in Advanced Mathematics, 39 (Cambridge University Press, Cambridge, 1993).Google Scholar
Buchweitz, R.-O., ‘Maximal Cohen–Macaulay modules and Tate-cohomology over Gorenstein rings’. Preprint.Google Scholar
Buchweitz, R.-O., Greuel, G.-M. and Schreyer, F.-O., ‘Cohen–Macaulay modules on hypersurface singularities. II’, Invent. Math. 88(1) (1987), 165–182.CrossRefGoogle Scholar
Chen, X., ‘Generalized Serre duality’, J. Algebra 328 (2011), 268–286.CrossRefGoogle Scholar
Curtis, C. and Reiner, I., Methods of Representation Theory. Vol. I. With Applications to Finite Groups and Orders, Pure and Applied Mathematics (A Wiley-Interscience Publication, John Wiley & Sons, Inc., New York, 1981).Google Scholar
Demonet, L. and Luo, X., ‘Ice quivers with potential associated with triangulations and Cohen–Macaulay modules over orders’, Trans. Amer. Math. Soc. 368(6) (2016), 4257–4293.CrossRefGoogle Scholar
Demonet, L. and Luo, X., ‘Ice quivers with potential arising from once-punctured polygons and Cohen–Macaulay modules’, Publ. Res. Inst. Math. Sci. 52(2) (2016), 141–205.CrossRefGoogle Scholar
Dieterich, E. and Wiedemann, A., ‘The Auslander–Reiten quiver of a simple curve singularity’, Trans. Amer. Math. Soc. 294(2) (1986), 455–475.CrossRefGoogle Scholar
Drozd, Y. A. and Greuel, G.-M., ‘Cohen–Macaulay module type’, Compos. Math. 89(3) (1993), 315–338.Google Scholar
Drozd, J. A. and Roĭter, A. V., ‘Commutative rings with a finite number of indecomposable integral representations’, Izv. Akad. Nauk SSSR Ser. Mat. 31 (1967), 783–798.Google Scholar
Eisenbud, D., ‘Homological algebra on a complete intersection, with an application to group representations’, Trans. Amer. Math. Soc. 260 (1980), 35–64.CrossRefGoogle Scholar
Futaki, M. and Ueda, K., ‘Homological mirror symmetry for Brieskorn–Pham singularities’, Selecta Math. (N.S.) 17(2) (2011), 435–452.CrossRefGoogle Scholar
Geigle, W. and Lenzing, H., ‘A class of weighted projective curves arising in representation theory of finite-dimensional algebras’, inSingularities, Representation of Algebras, and Vector Bundles (Lambrecht, 1985), Lecture Notes in Mathematics, 1273 (Springer, Berlin, 1987), 265–297.CrossRefGoogle Scholar
Geigle, W. and Lenzing, H., ‘Perpendicular categories with applications to representations and sheaves’, J. Algebra 144(2) (1991), 273–343.CrossRefGoogle Scholar
Gelinas, V., ‘Conic intersections, Maximal Cohen–Macaulay modules and the Four Subspace problem’. Preprint, 2017, arXiv:1702.06608.Google Scholar
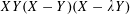Gelinas, V., ‘Betti tables for indecomposable matrix factorizations of $XY(X-Y)(X-\unicode[STIX]{x1D706}Y)$’. Preprint, 2017, arXiv:1712.07043.Google Scholar
Goto, S. and Watanabe, K., ‘On graded rings. I’, J. Math. Soc. Japan 30(2) (1978), 179–213.CrossRefGoogle Scholar
Greuel, G. M. and Knörrer, H., ‘Einfache Kurvensingularitäten und torsionsfreie Moduln’, Math. Ann. 270(3) (1985), 417–425.Google Scholar
Happel, D., Triangulated Categories in the Representation Theory of Finite-dimensional Algebras, London Mathematical Society Lecture Note Series, 119 (Cambridge University Press, Cambridge, 1988).CrossRefGoogle Scholar
Happel, D., ‘On Gorenstein algebras’, inRepresentation Theory of Finite Groups and Finite-dimensional Algebras (Bielefeld, 1991), Progress in Mathematics, 95 (Birkhäuser, Basel, 1991), 389–404.CrossRefGoogle Scholar
Herschend, M. and Iyama, O., ‘2-hereditary algebras and 3-Calabi–Yau algebras from hypersurface singularities’, in preparation.Google Scholar
Herschend, M., Iyama, O., Minamoto, H. and Oppermann, S., ‘Representation theory of Geigle-Lenzing complete intersections’, Mem. Amer. Math. Soc., to appear. Preprint, 2014,arXiv:1409.0668.Google Scholar
Herschend, M., Iyama, O. and Oppermann, S., ‘n-representation infinite algebras’, Adv. Math. 252 (2014), 292–342.CrossRefGoogle Scholar
Higashitani, A. and Ueyama, K., ‘Combinatorial study of stable categories of graded Cohen–Macaulay modules over skew quadric hypersurfaces’. Preprint, 2019, arXiv:1910.10612.Google Scholar
Hijikata, H. and Nishida, K., ‘Bass orders in nonsemisimple algebras’, J. Math. Kyoto Univ. 34(4) (1994), 797–837.CrossRefGoogle Scholar
Huybrechts, D., ‘Fourier–Mukai transforms in algebraic geometry’, inOxford Mathematical Monographs (The Clarendon Press, Oxford University Press, Oxford, 2006).Google Scholar
Iyama, O., ‘Tilting Cohen–Macaulay representations’, inProceedings of the International Congress of Mathematicians–Rio de Janeiro 2018. Vol. II, Invited Lectures (World Sci. Publ., Hackensack, NJ, 2018), 125–162.Google Scholar
Iyama, O. and Lerner, B., ‘Tilting bundles on orders on P d’, Israel J. Math. 211(1) (2016), 147–169.CrossRefGoogle Scholar
Iyama, O. and Oppermann, S., ‘Stable categories of higher preprojective algebras’, Adv. Math. 244 (2013), 23–68.CrossRefGoogle Scholar
Iyama, O. and Takahashi, R., ‘Tilting and cluster tilting for quotient singularities’, Math. Ann. 356(3) (2013), 1065–1105.Google Scholar
Iyama, O. and Yang, D., ‘Silting reduction and Calabi–Yau reduction of triangulated categories’, Trans. Amer. Math. Soc. 370(11) (2018), 7861–7898.CrossRefGoogle Scholar
Iyama, O. and Yang, D., ‘Quotients of triangulated categories and Equivalences of Buchweitz, Orlov and Amiot-Guo-Keller’, Amer. J. Math., to appear. Preprint, 2017, arXiv:1702.04475.Google Scholar
Jacobinski, H., ‘Sur les ordres commutatifs avec un nombre fini de réseaux indécomposables’, Acta Math. 118 (1967), 1–31.CrossRefGoogle Scholar
Jasso, G., ‘𝜏2 -stable tilting complexes over weighted projective lines’, Adv. Math. 273 (2015), 1–31.CrossRefGoogle Scholar
Jensen, B. T., King, A. and Su, X., ‘A categorification of Grassmannian cluster algebras’, Proc. Lond. Math. Soc. (3) 113(2) (2016), 185–212.CrossRefGoogle Scholar
Kajiura, H., Saito, K. and Takahashi, A., ‘Matrix factorization and representations of quivers. II. Type ADE case’, Adv. Math. 211(1) (2007), 327–362.CrossRefGoogle Scholar
Kajiura, H., Saito, K. and Takahashi, A., ‘Triangulated categories of matrix factorizations for regular systems of weights with 𝜖 = -1’, Adv. Math. 220(5) (2009), 1602–1654.CrossRefGoogle Scholar
Keller, B., ‘Deriving DG categories’, Ann. Sci. Éc. Norm. Supér. (4) 27(1) (1994), 63–102.CrossRefGoogle Scholar
Keller, B. and Krause, H., ‘Tilting preserves finite global dimension’, Comptes Rendus Math., to appear. Preprint, 2019, arXiv:1911.11749.Google Scholar
Keller, B. and Vossieck, D., ‘Aisles in derived categories’, Bull. Soc. Math. Belg. Ser. A 40(2) (1988), 239–253. Deuxieme Contact Franco-Belge en Algebre (Faulx-les-Tombes, 1987).Google Scholar
Kimura, Y., ‘Tilting theory of preprojective algebras and c-sortable elements’, J. Algebra 503 (2018), 186–221.CrossRefGoogle Scholar
Kimura, Y., ‘Tilting and cluster tilting for preprojective algebras and Coxeter groups’, Int. Math. Res. Not. IMRN 2019(18) (2019), 5597–5634.CrossRefGoogle Scholar
Kussin, D., Lenzing, H. and Meltzer, H., ‘Triangle singularities, ADE-chains, and weighted projective lines’, Adv. Math. 237 (2013), 194–251.CrossRefGoogle Scholar
Lenzing, H. and de la Pena, J. A., ‘Extended canonical algebras and Fuchsian singularities’, Math. Z. 268(1–2) (2011), 143–167.CrossRefGoogle Scholar
Leuschke, G. and Wiegand, R., Cohen–Macaulay Representations, Mathematical Surveys and Monographs, 181 (American Mathematical Society, Providence, RI, 2012).CrossRefGoogle Scholar
Lu, M. and Zhu, B., ‘Singularity categories of Gorenstein monomial algebras’. Preprint, 2017, arXiv:1708.00311.Google Scholar
Minamoto, H. and Yamaura, K., ‘On finitely graded Iwanaga–Gorenstein algebras and the stable categories of their (graded) Cohen–Macaulay modules’, Adv. Math., to appear. Preprint, 2018, arXiv:1812.03746.Google Scholar
Miyachi, J., ‘Duality for derived categories and cotilting bimodules’, J. Algebra 185(2) (1996), 583–603.CrossRefGoogle Scholar
Mizuno, Y., ‘APR tilting modules and graded quivers with potential’, Int. Math. Res. Not. IMRN 2014(3) (2014), 817–841.CrossRefGoogle Scholar
Mori, I. and Ueyama, K., ‘Stable categories of graded maximal Cohen–Macaulay modules over noncommutative quotient singularities’, Adv. Math. 297 (2016), 54–92.CrossRefGoogle Scholar
O’Carroll, L. and Popescu, D., ‘On a theorem of Knörrer concerning Cohen–Macaulay modules’, J. Pure Appl. Algebra 152(1–3) (2000), 293–302.CrossRefGoogle Scholar
Orlov, D. O., ‘Triangulated categories of singularities and D-branes in Landau-Ginzburg models’, Proc. Steklov Inst. Math. 3(246) (2004), 227–248.Google Scholar
Orlov, D., ‘Derived categories of coherent sheaves and triangulated categories of singularities’, inAlgebra, Arithmetic, and Geometry: in Honor of Yu. I. Manin. Vol. II, Progress in Mathematics, 270 (Birkhauser Boston Inc., Boston, MA, 2009), 503–531.CrossRefGoogle Scholar
Reiten, I. and Van den Bergh, M., ‘Noetherian hereditary abelian categories satisfying Serre duality’, J. Amer. Math. Soc. 15(2) (2002), 295–366.CrossRefGoogle Scholar
Rickard, J., ‘Morita theory for derived categories’, J. Lond. Math. Soc. (2) 39(3) (1989), 436–456.CrossRefGoogle Scholar
Ringel, C. M., Tame Algebras and Integral Quadratic Forms, Lecture Notes in Mathematics, 1099 (Springer, Berlin, 1984).CrossRefGoogle Scholar
Simson, D., Linear Representations of Partially Ordered Sets and Vector Space Categories, Algebra, Logic and Applications, 4 (Gordon and Breach Science Publishers, Montreux, 1992).Google Scholar
Skowronski, A., ‘Selfinjective algebras: finite and tame type’, inTrends in Representation Theory of Algebras and Related Topics, Contemporary Mathematics, 406 (American Mathematical Society, Providence, RI, 2006), 169–238.CrossRefGoogle Scholar
Smith, S. P. and Van den Bergh, M., ‘Noncommutative quadric surfaces’, J. Noncommut. Geom. 7(3) (2013), 817–856.CrossRefGoogle Scholar
Ueda, K., ‘Triangulated categories of Gorenstein cyclic quotient singularities’, Proc. Amer. Math. Soc. 136(8) (2008), 2745–2747.CrossRefGoogle Scholar
Ueda, K., ‘On graded stable derived categories of isolated Gorenstein quotient singularities’, J. Algebra 352 (2012), 382–391.CrossRefGoogle Scholar
Yamaura, K., ‘Realizing stable categories as derived categories’, Adv. Math. 248 (2013), 784–819.CrossRefGoogle Scholar
Yoshino, Y., Cohen–Macaulay Modules Over Cohen–Macaulay Rings, London Mathematical Society Lecture Note Series, 146 (Cambridge University Press, Cambridge, 1990).CrossRefGoogle Scholar