Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T15:35:22.108Z Has data issue: false hasContentIssue false
  • English
  • Français

TOPOLOGY ON COHOMOLOGY OF LOCAL FIELDS

Part of: Algebraic geometry: Foundations Algebraic number theory: local and $p$-adic fields

Published online by Cambridge University Press:  25 August 2015

KĘSTUTIS ČESNAVIČIUS
KĘSTUTIS ČESNAVIČIUS*
Affiliation:
Department of Mathematics, University of California, Berkeley, CA 94720-3840, USA; kestutis@berkeley.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Arithmetic duality theorems over a local field 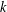$k$ are delicate to prove if 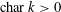$\text{char}\,k>0$. In this case, the proofs often exploit topologies carried by the cohomology groups 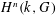$H^{n}(k,G)$ for commutative finite type 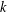$k$-group schemes 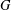$G$. These ‘Čech topologies’, defined using Čech cohomology, are impractical due to the lack of proofs of their basic properties, such as continuity of connecting maps in long exact sequences. We propose another way to topologize 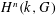$H^{n}(k,G)$: in the key case when 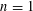$n=1$, identify 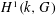$H^{1}(k,G)$ with the set of isomorphism classes of objects of the groupoid of 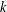$k$-points of the classifying stack 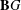$\mathbf{B}G$ and invoke Moret-Bailly’s general method of topologizing 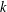$k$-points of locally of finite type 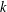$k$-algebraic stacks. Geometric arguments prove that these ‘classifying stack topologies’ enjoy the properties expected from the Čech topologies. With this as the key input, we prove that the Čech and the classifying stack topologies actually agree. The expected properties of the Čech topologies follow, and these properties streamline a number of arithmetic duality proofs given elsewhere.

MSC classification

Primary: 11S99: None of the above, but in this section
Secondary: 11S25: Galois cohomology 14A20: Generalizations (algebraic spaces, stacks)
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 3 , 2015 , e16
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2015

References

Artin, M., ‘Algebraization of formal moduli. I’, inGlobal Analysis (Papers in Honor of K. Kodaira) (University of Tokyo Press, Tokyo, 1969), 21–71; MR 0260746 (41 #5369).Google Scholar
Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron Models, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 21 (Springer, Berlin, 1990); MR 1045822 (91i:14034).Google Scholar
Bourbaki, N., Éléments de mathématique. Algèbre (chap. I-III, Hermann (1970); chap. IV-VII, Masson (1981); chap. VIII-X, Springer (2007, 2012) (in French)).Google Scholar
Bǎć, D. P. and Thǎńg, N. Q., ‘On the topology on group cohomology of algebraic groups over complete valued fields’, J. Algebra 399 (2014), 561–580; doi:10.1016/j.jalgebra.2013.08.041; MR 3144603.CrossRefGoogle Scholar
Conrad, B., Gabber, O. and Prasad, G., Pseudo-Reductive Groups, New Mathematical Monographs, 17 (Cambridge University Press, Cambridge, 2010); MR 2723571 (2011k:20093).Google Scholar
Conrad, B., Lieblich, M. and Olsson, M., ‘Nagata compactification for algebraic spaces’, J. Inst. Math. Jussieu 11(4) (2012), 747–814; doi:10.1017/S1474748011000223; MR 2979821.Google Scholar
Conrad, B., ‘Arithmetic moduli of generalized elliptic curves’, J. Inst. Math. Jussieu 6(2) (2007), 209–278; doi:10.1017/S1474748006000089; MR 2311664 (2008e:11073).Google Scholar
Conrad, B., ‘Deligne’s notes on Nagata compactifications’, J. Ramanujan Math. Soc. 22(3) (2007), 205–257; MR 2356346 (2009d:14002).Google Scholar
Conrad, B., ‘Weil and Grothendieck approaches to adelic points’, Enseign. Math. (2) 58(1–2) (2012), 61–97; MR 2985010.CrossRefGoogle Scholar
Grothendieck, A. and Dieudonné, J., ‘Éléments de géométrie algébrique. II. Étude globale élémentaire de quelques classes de morphismes’, Publ. Math. Inst. Hautes Études Sci. (8) (1961), 222 (in French); MR 0163909 (29 #1208).Google Scholar
Grothendieck, A. and Dieudonné, J., ‘Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. I’, Publ. Math. Inst. Hautes Études Sci. (20) (1964), 259 (in French); MR 0173675 (30 #3885).Google Scholar
Grothendieck, A. and Dieudonné, J., ‘Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. II’, Publ. Math. Inst. Hautes Études Sci. (24) (1965), 231 (in French); MR 0199181 (33 #7330).Google Scholar
Grothendieck, A. and Dieudonné, J., ‘Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas. III’, Publ. Math. Inst. Hautes Études Sci. (28) (1966), 255; MR 0217086 (36 #178).Google Scholar
Grothendieck, A. and Dieudonné, J., ‘Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas IV’, Publ. Math. Inst. Hautes Études Sci. (32) (1967), 361 (in French); MR 0238860 (39 #220).Google Scholar
Faltings, G. and Chai, C.-L., Degeneration of Abelian Varieties, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 22 (Springer, Berlin, 1990). With an appendix by David Mumford; MR 1083353 (92d:14036).Google Scholar
Giraud, J., Cohomologie non abélienne, Die Grundlehren der mathematischen Wissenschaften, Band 179 (Springer, Berlin, 1971) (in French);MR 0344253 (49 #8992).CrossRefGoogle Scholar
Gabber, O., Gille, P. and Moret-Bailly, L., ‘Fibrés principaux sur les corps valués henséliens’, Algebr. Geom. 1(5) (2014), 573–612 (French, with English and French summaries); MR 3296806.Google Scholar
Grothendieck, A., Technique de descente et théorèmes d’existence en géometrie algébrique. I. Généralités. Descente par morphismes fidèlement plats, Séminaire Bourbaki, Exp. No. 190, Vol. 5 (Société Mathématique de France, Paris, 1995), 299–327. (in French); MR 1603475.Google Scholar
Grothendieck, A., ‘Le groupe de Brauer. III. Exemples et compléments’, inDix Exposés sur la Cohomologie des Schémas (North-Holland, Amsterdam, 1968), 88–188 (in French); MR 0244271 (39 #5586c).Google Scholar
Illusie, L. and Zheng, W., ‘Quotient stacks and equivariant étale cohomology algebras: Quillen’s theory revisited’, J. Algebraic Geom. to appear, (2015), available at arXiv:abs/1305.0365.Google Scholar
Knutson, D., Algebraic Spaces, Lecture Notes in Mathematics, 203 (Springer, Berlin, 1971); MR 0302647 (46 #1791).Google Scholar
Laumon, G. and Moret-Bailly, L., Champs Algébriques, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], 39 (Springer, Berlin, 2000) (in French);MR 1771927 (2001f:14006).CrossRefGoogle Scholar
Moret-Bailly, L., ‘Problèmes de Skolem sur les champs algébriques’, Compositio Math. 125(1) (2001), 1–30 (French, with English summary); MR 1818054 (2002c:11067); doi:10.1023/A:1002686625404.Google Scholar
Moret-Bailly, L., ‘Un théorème de l’application ouverte sur les corps valués algébriquement clos’, Math. Scand. 111(2) (2012), 161–168 (French, with English and French summaries); MR 3023520.Google Scholar
Milne, J. S., Arithmetic Duality Theorems, 2nd edn (BookSurge, LLC, Charleston, SC, 2006); MR 2261462 (2007e:14029).Google Scholar
Olsson, M. C., ‘Hom -stacks and restriction of scalars’, Duke Math. J. 134(1) (2006), 139–164; doi:10.1215/S0012-7094-06-13414-2; MR 2239345 (2007f:14002).Google Scholar
Serre, J.-P., Galois Cohomology, Springer Monographs in Mathematics, Corrected reprint of the 1997 English edition (Springer, Berlin, 2002) Translated from the French by Patrick Ion and revised by the author; MR 1867431 (2002i:12004).Google Scholar
Gille, P. and Polo, P. (Eds.), Schémas en groupes (SGA 3). Tome I. Propriétés générales des schémas en groupes, Documents Mathématiques (Paris) [Mathematical Documents (Paris)], 7 (Société Mathématique de France, Paris, 2011) (in French). Séminaire de Géométrie Algébrique du Bois Marie 1962–64. [Algebraic Geometry Seminar of Bois Marie 1962–64]; A seminar directed by M. Demazure and A. Grothendieck with the collaboration of M. Artin, J.-E. Bertin, P. Gabriel, M. Raynaud and J.-P. Serre; Revised and annotated edition of the 1970 French original; MR 2867621.Google Scholar
Gille, P. and Polo, P. (Eds.), Schémas en groupes (SGA 3). Tome III. Structure des schémas en groupes réductifs, Documents Mathématiques (Paris) [Mathematical Documents (Paris)], 8 (Société Mathématique de France, Paris, 2011) (in French). Séminaire de Géométrie Algébrique du Bois Marie 1962–64. [Algebraic Geometry Seminar of Bois Marie 1962–64]; A seminar directed by M. Demazure and A. Grothendieck with the collaboration of M. Artin, J.-E. Bertin, P. Gabriel, M. Raynaud and J.-P. Serre; Revised and annotated edition of the 1970 French original; MR 2867622.Google Scholar
Théorie des topos et cohomologie étale des schémas. Tome 2, Lecture Notes in Mathematics, 270 (Springer, Berlin, 1972) (in French). Séminaire de Géométrie Algébrique du Bois-Marie 1963–1964 (SGA 4); Dirigé par M. Artin, A. Grothendieck et J. L. Verdier. Avec la collaboration de N. Bourbaki, P. Deligne et B. Saint-Donat; MR 0354653 (50 #7131).Google Scholar
Shatz, S. S., ‘Cohomology of artinian group schemes over local fields’, Ann. of Math. (2) 79 (1964), 411–449; MR 0193093 (33 #1314).Google Scholar
Shatz, S. S., Profinite Groups, Arithmetic, and Geometry, Annals of Mathematics Studies, 67 (Princeton University Press, Princeton, NJ; University of Tokyo Press, Tokyo, 1972); MR 0347778 (50 #279).Google Scholar
de Jong, A. J. et al. , The Stacks Project. http://stacks.math.columbia.edu.Google Scholar
Toën, B., ‘Descente fidèlement plate pour les n-champs d’Artin’, Compos. Math. 147(5) (2011), 1382–1412 (French, with English and French summaries); doi:10.1112/S0010437X10005245; MR 2834725.Google Scholar