Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T12:56:57.106Z Has data issue: false hasContentIssue false
  • English
  • Français

TRANSFERENCE FOR THE ERDŐS–KO–RADO THEOREM

Part of: Graph theory Extremal combinatorics

Published online by Cambridge University Press:  26 October 2015

JÓZSEF BALOGH ,
BÉLA BOLLOBÁS  and
BHARGAV P. NARAYANAN
JÓZSEF BALOGH
Affiliation:
Department of Mathematics, University of Illinois, 1409 W. Green Street, Urbana, IL 61801, USA Bolyai Institute, University of Szeged, 6720 Szeged, Hungary; jobal@math.uiuc.edu
BÉLA BOLLOBÁS
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WB, UK; b.p.narayanan@dpmms.cam.ac.uk Department of Mathematical Sciences, University of Memphis, Memphis, TN 38152, USA London Institute for Mathematical Sciences, 35a South St., Mayfair, London W1K 2XF, UK; b.bollobas@dpmms.cam.ac.uk
BHARGAV P. NARAYANAN
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WB, UK; b.p.narayanan@dpmms.cam.ac.uk

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For natural numbers 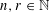$n,r\in \mathbb{N}$ with 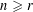$n\geqslant r$, the Kneser graph 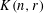$K(n,r)$ is the graph on the family of $r$-element subsets of 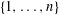$\{1,\ldots ,n\}$ in which two sets are adjacent if and only if they are disjoint. Delete the edges of 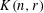$K(n,r)$ with some probability, independently of each other: is the independence number of this random graph equal to the independence number of the Kneser graph itself? We shall answer this question affirmatively as long as 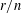$r/n$ is bounded away from 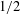$1/2$, even when the probability of retaining an edge of the Kneser graph is quite small. This gives us a random analogue of the Erdős–Ko–Rado theorem, since an independent set in the Kneser graph is the same as a uniform intersecting family. To prove our main result, we give some new estimates for the number of disjoint pairs in a family in terms of its distance from an intersecting family; these might be of independent interest.

MSC classification

Primary: 05D05: Extremal set theory
Secondary: 05C80: Random graphs 05D40: Probabilistic methods
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 3 , 2015 , e23
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2015

References

Babai, L., Simonovits, M. and Spencer, J., ‘Extremal subgraphs of random graphs’, J. Graph Theory 14 (1990), 599–622.CrossRefGoogle Scholar
Balogh, J., Bohman, T. and Mubayi, D., ‘Erdős–Ko–Rado in random hypergraphs’, Combin. Probab. Comput. 18 (2009), 629–646.Google Scholar
Balogh, J., Das, S., Delcourt, M., Liu, H. and Sharifzadeh, M., ‘The typical structure of intersecting families of discrete structures’, J. Combin. Theory Ser. A 132 (2015), 224–245.Google Scholar
Balogh, J., Morris, R. and Samotij, W., ‘Independent sets in hypergraphs’, J. Amer. Math. Soc. 28(3) (2015), 669–709.Google Scholar
Bogolyubskiy, L. I., Gusev, A. S., Pyaderkin, M. M. and Raigorodskii, A. M., ‘The independence numbers and the chromatic numbers of random subgraphs of some distance graphs’, Mat. Sb. (to appear).Google Scholar
Bollobás, B., ‘On generalized graphs’, Acta Math. Acad. Sci. Hungar 16 (1965), 447–452.Google Scholar
Bollobás, B., Narayanan, B. P. and Raigorodskii, A. M., ‘On the stability of the Erdős–Ko–Rado theorem’. J. Combin. Theory Ser. A (to appear).Google Scholar
Conlon, D. and Gowers, T., ‘Combinatorial theorems in sparse random sets’, Ann. of Math. (2) (to appear).Google Scholar
Das, S. and Tran, T., ‘A simple removal lemma for large nearly-intersecting families’, Preprint, arXiv:1412.7885.Google Scholar
Devlin, P. and Kahn, J., ‘On “stability” in the Erdős–Ko–Rado theorem’, Preprint,arXiv:1502.05692.Google Scholar
Dinur, I. and Friedgut, E., ‘Intersecting families are essentially contained in juntas’, Combin. Probab. Comput. 18 (2009), 107–122.Google Scholar
Erdős, P., Ko, C. and Rado, R., ‘Intersection theorems for systems of finite sets’, Quart. J. Math. Oxford 12 (1961), 313–320.Google Scholar
Friedgut, E., ‘On the measure of intersecting families, uniqueness and stability’, Combinatorica 28 (2008), 503–528.Google Scholar
Hamm, A. and Kahn, J., ‘On Erdős–Ko–Rado for random hypergraphs II’, Preprint,arXiv:1406.5793.Google Scholar
Hilton, A. J. W. and Milner, E. C., ‘Some intersection theorems for systems of finite sets’, Quart. J. Math. Oxford 18 (1967), 369–384.Google Scholar
Katona, G., ‘A theorem of finite sets’, inTheory of Graphs (Proc. Colloq., Tihany, 1966) (Academic Press, New York, 1968), 187–207.Google Scholar
Keevash, P., ‘Shadows and intersections: stability and new proofs’, Adv. Math. 218(5) (2008), 1685–1703.Google Scholar
Keevash, P. and Mubayi, D., ‘Set systems without a simplex or a cluster’, Combinatorica 30 (2010), 175–200.Google Scholar
Kleitman, D. J. and Winston, K. J., ‘On the number of graphs without 4-cycles’, Discrete Math. 41 (1982), 167–172.Google Scholar
Kohayakawa, Y., Łuczak, T. and Rödl, V., ‘Arithmetic progressions of length three in subsets of a random set’, Acta Arith. 75 (1996), 133–163.Google Scholar
Kruskal, J. B., ‘The number of simplices in a complex’, inMathematical Optimization Techniques (University of California Press, Berkeley, CA, 1963), 251–278.Google Scholar
Lovász, L., ‘On the Shannon capacity of a graph’, IEEE Trans. Inform. Theory 25 (1979), 1–7.Google Scholar
Lovász, L., Combinatorial Problems and Exercises, 2nd edn (AMS Chelsea Publishing, Providence, RI, 2007).Google Scholar
Łuczak, T., ‘Randomness and regularity’, inInternational Congress of Mathematicians, III (European Mathematical Society, Zürich, 2006), 899–909.Google Scholar
Rödl, V. and Ruciński, A., ‘Threshold functions for Ramsey properties’, J. Amer. Math. Soc. 8 (1995), 917–942.Google Scholar
Rödl, V. and Ruciński, A., ‘Rado partition theorem for random subsets of integers’, Proc. Lond. Math. Soc. 74 (1997), 481–502.Google Scholar
Rödl, V. and Schacht, M., ‘Extremal results in random graphs’, inErdős Centennial, Bolyai Society Mathematical Studies, 25 (Springer, Berlin, Heidelberg, 2013), 535–583.CrossRefGoogle Scholar
Saxton, D. and Thomason, A., ‘Hypergraph containers’, Preprint, arXiv:1204.6595.Google Scholar
Schacht, M., ‘Extremal results for random discrete structures’, Ann. of Math. (2) (to appear).Google Scholar