Article contents
THE TYPICAL STRUCTURE OF MAXIMAL TRIANGLE-FREE GRAPHS
Published online by Cambridge University Press: 09 October 2015
Abstract
Recently, settling a question of Erdős, Balogh, and Petříčková showed that there are at most 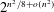 $2^{n^{2}/8+o(n^{2})}$
$2^{n^{2}/8+o(n^{2})}$ $n$-vertex maximal triangle-free graphs, matching the previously known lower bound. Here, we characterize the typical structure of maximal triangle-free graphs. We show that almost every maximal triangle-free graph
$n$-vertex maximal triangle-free graphs, matching the previously known lower bound. Here, we characterize the typical structure of maximal triangle-free graphs. We show that almost every maximal triangle-free graph 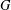 $G$ admits a vertex partition
$G$ admits a vertex partition 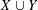 $X\cup Y$ such that
$X\cup Y$ such that 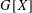 $G[X]$ is a perfect matching and
$G[X]$ is a perfect matching and 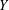 $Y$ is an independent set.
$Y$ is an independent set.
Our proof uses the Ruzsa–Szemerédi removal lemma, the Erdős–Simonovits stability theorem, and recent results of Balogh, Morris, and Samotij and Saxton and Thomason on characterization of the structure of independent sets in hypergraphs. The proof also relies on a new bound on the number of maximal independent sets in triangle-free graphs with many vertex-disjoint 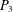 $P_{3}$s, which is of independent interest.
$P_{3}$s, which is of independent interest.
MSC classification
Information
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2015
References
- 4
- Cited by


