Published online by Cambridge University Press: 02 December 2015
We prove global well-posedness of the time-dependent degenerate thermistor problem by establishing a uniform-in-time bounded mean ocsillation (BMO) estimate of inhomogeneous parabolic equations. Applying this estimate to the temperature equation, we derive a BMO bound of the temperature uniform with respect to time, which implies that the electric conductivity is an 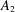 $A_{2}$ weight. The Hölder continuity of the electric potential is then proved by applying the De Giorgi–Nash–Moser estimate for degenerate elliptic equations with an
$A_{2}$ weight. The Hölder continuity of the electric potential is then proved by applying the De Giorgi–Nash–Moser estimate for degenerate elliptic equations with an 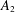 $A_{2}$ coefficient. The uniqueness of the solution is proved based on the established regularity of the weak solution. Our results also imply the existence of a global classical solution when the initial and boundary data are smooth.
$A_{2}$ coefficient. The uniqueness of the solution is proved based on the established regularity of the weak solution. Our results also imply the existence of a global classical solution when the initial and boundary data are smooth.