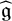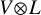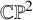1 Introduction
In [Reference Bershtein, Feigin and LitvinovBFL16] Bershtein, Litvinov and the third named author introduced the Urod algebra, which gives a representation theoretic interpretation of the celebrated Nakajima–Yoshioka blowup equations [Reference Nakajima and YoshiokaNY05] for the moduli space of framed torsion free sheaves on ![]() $\mathbb {CP}^{2}$ of rank two via the Alday–Gaiotto–Tachikawa (AGT) correspondence [Reference Alday, Gaiotto and TachikawaAGT10]. One of the aims of the present paper is to introduce the higher-rank Urod algebras, which generalizes the result of [Reference Bershtein, Feigin and LitvinovBFL16] to the case of sheaves at arbitrary rank.
$\mathbb {CP}^{2}$ of rank two via the Alday–Gaiotto–Tachikawa (AGT) correspondence [Reference Alday, Gaiotto and TachikawaAGT10]. One of the aims of the present paper is to introduce the higher-rank Urod algebras, which generalizes the result of [Reference Bershtein, Feigin and LitvinovBFL16] to the case of sheaves at arbitrary rank.
In fact, it turned out in recent works (see, e.g., [Reference Feigin and GukovFG18, Reference Creutzig and GaiottoCG17]) that Urod algebras appear not only in the AGT correspondence but also in various theories of vertex algebras in connection with higher-dimensional quantum field theories. This work provides the first systematic study of Urod algebras appearing in various contexts.
Another aim of this paper is to introduce the translation for (affine) W-algebras. Namely, we show that any integrable highest representation L of level ![]() $\ell \in \mathbb {Z}_{>0}$ gives rise to an exact functor
$\ell \in \mathbb {Z}_{>0}$ gives rise to an exact functor
where ![]() $\mathscr {W}^{k}(\mathfrak {g},f)$ is the W-algebra associated with
$\mathscr {W}^{k}(\mathfrak {g},f)$ is the W-algebra associated with ![]() $\mathfrak {g}$ and its nilpotent element f at level
$\mathfrak {g}$ and its nilpotent element f at level ![]() $k\in \mathbb {C}$ ([Reference Feigin and FrenkelFF90a, Reference Kac, Roan and WakimotoKRW03]).
$k\in \mathbb {C}$ ([Reference Feigin and FrenkelFF90a, Reference Kac, Roan and WakimotoKRW03]).
We establish these results by showing that the quantized Drinfeld–Sokolov reduction commutes with tensoring with integrable representations.
Let us describe our results in more details.
1.1 Main Theorem
Let ![]() $\mathfrak {g}$ be a simple Lie algebra,
$\mathfrak {g}$ be a simple Lie algebra, ![]() $\widehat {\mathfrak {g}}=\mathfrak {g}((t))\mathop {\oplus }\mathbb {C} K$ be the affine Kac–Moody Lie algebra associated with
$\widehat {\mathfrak {g}}=\mathfrak {g}((t))\mathop {\oplus }\mathbb {C} K$ be the affine Kac–Moody Lie algebra associated with ![]() $\mathfrak {g}$ defined by the commutation relation
$\mathfrak {g}$ defined by the commutation relation
![]() $[K,\widehat {\mathfrak {g}}]=0$, where
$[K,\widehat {\mathfrak {g}}]=0$, where ![]() $(~|~)$ is the normalized inner product of
$(~|~)$ is the normalized inner product of ![]() $\mathfrak {g}$ (it is
$\mathfrak {g}$ (it is ![]() $1/2h^{\vee }$ times the Killing form of
$1/2h^{\vee }$ times the Killing form of ![]() $\mathfrak {g}$, where
$\mathfrak {g}$, where ![]() $h^{\vee }$ is the dual Coxeter number of
$h^{\vee }$ is the dual Coxeter number of ![]() $\mathfrak {g}$). For
$\mathfrak {g}$). For ![]() $k\in \mathbb {C}$, let
$k\in \mathbb {C}$, let ![]() $V^{k}(\mathfrak {g})=U(\widehat {\mathfrak {g}}){\otimes }_{U(\mathfrak {g}[[t]]{\otimes } \mathbb {C} K)}\mathbb {C}$, where
$V^{k}(\mathfrak {g})=U(\widehat {\mathfrak {g}}){\otimes }_{U(\mathfrak {g}[[t]]{\otimes } \mathbb {C} K)}\mathbb {C}$, where ![]() $\mathbb {C}$ is regarded as a one-dimensional representation of
$\mathbb {C}$ is regarded as a one-dimensional representation of ![]() $\mathfrak {g}[[t]]{\otimes } \mathbb {C} K$ on which
$\mathfrak {g}[[t]]{\otimes } \mathbb {C} K$ on which ![]() $\mathfrak {g}[[t]]$ acts trivially and K acts via multiplication by k.
$\mathfrak {g}[[t]]$ acts trivially and K acts via multiplication by k. ![]() $V^{k}(\mathfrak {g})$ is naturally a vertex algebra and is called the universal affine vertex algebra associated with
$V^{k}(\mathfrak {g})$ is naturally a vertex algebra and is called the universal affine vertex algebra associated with ![]() $\mathfrak {g}$ at level k.
$\mathfrak {g}$ at level k.
Any (graded) quotient V of ![]() $V^{k}(\mathfrak {g})$ inherits the vertex algebra structure from
$V^{k}(\mathfrak {g})$ inherits the vertex algebra structure from ![]() $V^{k}(\mathfrak {g})$. Let
$V^{k}(\mathfrak {g})$. Let ![]() $\mathbb {L}_{k}(\mathfrak {g})$ be the unique simple (graded) quotient of
$\mathbb {L}_{k}(\mathfrak {g})$ be the unique simple (graded) quotient of ![]() $V^{k}(\mathfrak {g})$. The vertex algebra
$V^{k}(\mathfrak {g})$. The vertex algebra ![]() $\mathbb {L}_{k}(\mathfrak {g})$ is integrable as an
$\mathbb {L}_{k}(\mathfrak {g})$ is integrable as an ![]() $\widehat {\mathfrak {g}}$-module if and only if
$\widehat {\mathfrak {g}}$-module if and only if ![]() $k\in \mathbb {Z}_{\geqslant 0}$.
$k\in \mathbb {Z}_{\geqslant 0}$.
For a nilpotent element f of ![]() $\mathfrak {g}$, let
$\mathfrak {g}$, let ![]() $H_{DS,f}^{\bullet }(M)$ be the BRST cohomology of the quantized Drinfeld–Sokolov reduction associated with
$H_{DS,f}^{\bullet }(M)$ be the BRST cohomology of the quantized Drinfeld–Sokolov reduction associated with ![]() $(\mathfrak {g},f)$ with coefficients in a
$(\mathfrak {g},f)$ with coefficients in a ![]() $\widehat {\mathfrak {g}}$-module M ([Reference Feigin and FrenkelFF90a, Reference Kac, Roan and WakimotoKRW03]). The W-algebra associated with
$\widehat {\mathfrak {g}}$-module M ([Reference Feigin and FrenkelFF90a, Reference Kac, Roan and WakimotoKRW03]). The W-algebra associated with ![]() $(\mathfrak {g},f)$ at level k is by definition the vertex algebra
$(\mathfrak {g},f)$ at level k is by definition the vertex algebra
For any smooth ![]() $\widehat {\mathfrak {g}}$-module M of level k,
$\widehat {\mathfrak {g}}$-module M of level k, ![]() $H_{DS,f}^{i}(M)$,
$H_{DS,f}^{i}(M)$, ![]() $i\in \mathbb {Z}$, is a module over
$i\in \mathbb {Z}$, is a module over ![]() $\mathscr {W}^{k}(\mathfrak {g},f)$. More generally, for any vertex algebra V equipped with a vertex algebra homomorphism
$\mathscr {W}^{k}(\mathfrak {g},f)$. More generally, for any vertex algebra V equipped with a vertex algebra homomorphism ![]() $V^{k}(\mathfrak {g})\rightarrow V$ and a V-module M,
$V^{k}(\mathfrak {g})\rightarrow V$ and a V-module M, ![]() $H_{DS,f}^{i}(M)$,
$H_{DS,f}^{i}(M)$, ![]() $i\in \mathbb {Z}$, is a module over the vertex algebra
$i\in \mathbb {Z}$, is a module over the vertex algebra ![]() $H_{DS,f}^{0}(V)$.
$H_{DS,f}^{0}(V)$.
Theorem 1. Let V be a quotient of the universal affine vertex algebra ![]() $V^{k}(\mathfrak {g})$ and
$V^{k}(\mathfrak {g})$ and ![]() $\ell \in \mathbb {Z}_{\geqslant 0}$. We have a vertex algebra isomorphism
$\ell \in \mathbb {Z}_{\geqslant 0}$. We have a vertex algebra isomorphism
where in the left-hand-side the Drinfeld–Sokolov reduction is taken with respect to the diagonal action of ![]() $\widehat {\mathfrak {g}}$ on
$\widehat {\mathfrak {g}}$ on ![]() $V{\otimes } \mathbb {L}_{\ell }(\mathfrak {g})$. More generally, let V be a vertex algebra equipped with a vertex algebra homomorphism
$V{\otimes } \mathbb {L}_{\ell }(\mathfrak {g})$. More generally, let V be a vertex algebra equipped with a vertex algebra homomorphism ![]() $V^{k}(\mathfrak {g})\rightarrow V$. Then we have an isomorphism
$V^{k}(\mathfrak {g})\rightarrow V$. Then we have an isomorphism
of graded vertex algebras, and for any V-module M, ![]() $ \mathbb {L}_{\ell }(\mathfrak {g})$-module N, there is an isomorphism
$ \mathbb {L}_{\ell }(\mathfrak {g})$-module N, there is an isomorphism
as modules over ![]() $H_{DS,f}^{\bullet }(V\otimes \mathbb {L}_{\ell }(\mathfrak {g}))\cong H_{DS,f}^{\bullet }(V)\otimes \mathbb {L}_{\ell }(\mathfrak {g})$.
$H_{DS,f}^{\bullet }(V\otimes \mathbb {L}_{\ell }(\mathfrak {g}))\cong H_{DS,f}^{\bullet }(V)\otimes \mathbb {L}_{\ell }(\mathfrak {g})$.
In the case that ![]() $\mathfrak {g}=\mathfrak {sl}_{2}$ and
$\mathfrak {g}=\mathfrak {sl}_{2}$ and ![]() $\ell =1$, the isomorphism (30) was established in [Reference Bershtein, Feigin and LitvinovBFL16]. Our argument only requires certain properties of integrable representations and especially also works for superalgebras as well; see Section 5.
$\ell =1$, the isomorphism (30) was established in [Reference Bershtein, Feigin and LitvinovBFL16]. Our argument only requires certain properties of integrable representations and especially also works for superalgebras as well; see Section 5.
We note that the existence of the isomorphism (30) as vector spaces is not difficult to see. However, it is not a priori clear at all why there should exist an isomorphism of vertex algebras. We also note that equation (30) is not compatible with the standard conformal gradings of both sides. To remedy this, we need to change the conformal vector of ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$ on the right-hand side to a new conformal vector
$\mathbb {L}_{\ell }(\mathfrak {g})$ on the right-hand side to a new conformal vector ![]() $\omega _{Urod}$, which we call the Urod conformal vector (see Section 6).
$\omega _{Urod}$, which we call the Urod conformal vector (see Section 6).
The proof of Theorem 1 is based on some new construction of automorphisms of vertex algebras, which may be of independent interest; see Section 2 for the details.
1.2 Translation for W-algebras
By applying Theorem 1 to ![]() $V=V^{k}(\mathfrak {g})$,
$V=V^{k}(\mathfrak {g})$, ![]() $k\in \mathbb {C}$, we obtain the vertex algebra isomorphism
$k\in \mathbb {C}$, we obtain the vertex algebra isomorphism
Consequently, the natural vertex algebra homomorphism ![]() $V^{k+\ell }(\mathfrak {g})\rightarrow V^{k}(\mathfrak {g}){\otimes } \mathbb {L}_{\ell }(\mathfrak {g})$ induces a vertex algebra homomorphism
$V^{k+\ell }(\mathfrak {g})\rightarrow V^{k}(\mathfrak {g}){\otimes } \mathbb {L}_{\ell }(\mathfrak {g})$ induces a vertex algebra homomorphism
Therefore, for any ![]() $\mathscr {W}^{k}(\mathfrak {g},f)$-module M and any integrable representation L of
$\mathscr {W}^{k}(\mathfrak {g},f)$-module M and any integrable representation L of ![]() $\widehat {\mathfrak {g}}$ of level
$\widehat {\mathfrak {g}}$ of level ![]() $\ell $,
$\ell $, ![]() $M{\otimes }L$ is has the structure of an
$M{\otimes }L$ is has the structure of an ![]() $\mathscr {W}^{k+\ell }(\mathfrak {g},f)$-module. As a consequence, we obtain the translation by L, that is, the exact functor (1) as we wished.
$\mathscr {W}^{k+\ell }(\mathfrak {g},f)$-module. As a consequence, we obtain the translation by L, that is, the exact functor (1) as we wished.
Recall that the Zhu algebra of ![]() $\mathscr {W}^{k}(\mathfrak {g},f)$ is isomorphic to the finite W-algebra [Reference PremetPre02]
$\mathscr {W}^{k}(\mathfrak {g},f)$ is isomorphic to the finite W-algebra [Reference PremetPre02] ![]() $U(\mathfrak {g},f)$ associated with
$U(\mathfrak {g},f)$ associated with ![]() $(\mathfrak {g},f)$ ([Reference ArakawaAra07, Reference De Sole and KacDSK06]). Also, the Zhu algebra of
$(\mathfrak {g},f)$ ([Reference ArakawaAra07, Reference De Sole and KacDSK06]). Also, the Zhu algebra of ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$ is isomorphic to the quotient
$\mathbb {L}_{\ell }(\mathfrak {g})$ is isomorphic to the quotient ![]() $U_{\ell }(\mathfrak {g})$ of
$U_{\ell }(\mathfrak {g})$ of ![]() $U(\mathfrak {g})$ by the two-sided ideal generated by
$U(\mathfrak {g})$ by the two-sided ideal generated by ![]() $e_{\theta }^{\ell +1}$ ([Reference Frenkel and ZhuFZ92]), and so is that of
$e_{\theta }^{\ell +1}$ ([Reference Frenkel and ZhuFZ92]), and so is that of ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$ with the Urod conformal structure ([Reference ArakawaAra15b]). Therefore, by taking the Zhu algebras, we obtain from equation (1) an algebra homomorphism
$\mathbb {L}_{\ell }(\mathfrak {g})$ with the Urod conformal structure ([Reference ArakawaAra15b]). Therefore, by taking the Zhu algebras, we obtain from equation (1) an algebra homomorphism
Since any finite-dimensional ![]() $\mathfrak {g}$-module is an
$\mathfrak {g}$-module is an ![]() $U_{\ell }(\mathfrak {g})$-module for a sufficiently large
$U_{\ell }(\mathfrak {g})$-module for a sufficiently large ![]() $\ell $, equation (4) gives
$\ell $, equation (4) gives ![]() $M{\otimes } E$ a structure of
$M{\otimes } E$ a structure of ![]() $U(\mathfrak {g},f)$-module for any
$U(\mathfrak {g},f)$-module for any ![]() $U(\mathfrak {g},f)$-module M and a finite-dimensional
$U(\mathfrak {g},f)$-module M and a finite-dimensional ![]() $\mathfrak {g}$-module E. We expect that this
$\mathfrak {g}$-module E. We expect that this ![]() $U(\mathfrak {g},f)$-module structure of
$U(\mathfrak {g},f)$-module structure of ![]() $M{\otimes } E$ does not depend on the choice of a sufficiently large
$M{\otimes } E$ does not depend on the choice of a sufficiently large ![]() $\ell $, and coincides with the one obtained by Goodwin [Reference GoodwinGoo11].
$\ell $, and coincides with the one obtained by Goodwin [Reference GoodwinGoo11].
1.3 Higher-rank Urod algebras
We denote also by ![]() $\mathscr {W}^{k}(\mathfrak {g})$ the W-algebra
$\mathscr {W}^{k}(\mathfrak {g})$ the W-algebra ![]() $\mathscr {W}^{k}(\mathfrak {g},f_{prin})$ associated with a principal nilpotent element
$\mathscr {W}^{k}(\mathfrak {g},f_{prin})$ associated with a principal nilpotent element ![]() $f_{prin}$ of
$f_{prin}$ of ![]() $\mathfrak {g}$. Let
$\mathfrak {g}$. Let ![]() $\mathfrak {g}$ be simply laced, and suppose that
$\mathfrak {g}$ be simply laced, and suppose that ![]() $k+h^{\vee }-1\not \in \mathbb {Q}_{\leqslant 0}$, where
$k+h^{\vee }-1\not \in \mathbb {Q}_{\leqslant 0}$, where ![]() $h^{\vee }$ is the dual Coxeter number of
$h^{\vee }$ is the dual Coxeter number of ![]() $\mathfrak {g}$. By the coset construction [Reference Arakawa, Creutzig and LinshawACL19] of the principal W-algebra
$\mathfrak {g}$. By the coset construction [Reference Arakawa, Creutzig and LinshawACL19] of the principal W-algebra ![]() $\mathscr {W}^{k}(\mathfrak {g})$, we have a conformal vertex algebra embedding
$\mathscr {W}^{k}(\mathfrak {g})$, we have a conformal vertex algebra embedding
where ![]() $\ell $ is the number defined by the formula
$\ell $ is the number defined by the formula
By taking the Drinfeld–Sokolov reduction with respect to the level k action of ![]() $\widehat {\mathfrak {g}}$, equation (5) gives rise to the full vertex algebra embedding
$\widehat {\mathfrak {g}}$, equation (5) gives rise to the full vertex algebra embedding
where the last isomorphism follows from Theorem 1 and ![]() $\mathcal {U}(\mathfrak {g})=\mathcal {U}(\mathfrak {g},f)$ is the vertex algebra
$\mathcal {U}(\mathfrak {g})=\mathcal {U}(\mathfrak {g},f)$ is the vertex algebra ![]() $\mathbb {L}_{1}(\mathfrak {g})$ equipped with the Urod conformal vector
$\mathbb {L}_{1}(\mathfrak {g})$ equipped with the Urod conformal vector ![]() $\omega _{Urod}$. We call the vertex operator algebra
$\omega _{Urod}$. We call the vertex operator algebra ![]() $\mathcal {U}(\mathfrak {g})$ the Urod algebra. In the case that
$\mathcal {U}(\mathfrak {g})$ the Urod algebra. In the case that ![]() $\mathfrak {g}=\mathfrak {sl}_{2}$ and
$\mathfrak {g}=\mathfrak {sl}_{2}$ and ![]() $f=f_{prin}$,
$f=f_{prin}$, ![]() $\mathcal {U}(\mathfrak {g})$ is exactly the Urod algebra introduced in [Reference Bershtein, Feigin and LitvinovBFL16].
$\mathcal {U}(\mathfrak {g})$ is exactly the Urod algebra introduced in [Reference Bershtein, Feigin and LitvinovBFL16].
Let L be a level one integrable representation of ![]() $\widehat {\mathfrak {g}}$, which is naturally a module over the Urod algebra
$\widehat {\mathfrak {g}}$, which is naturally a module over the Urod algebra ![]() $\mathcal {U}(\mathfrak {g})$. By equation (43), for any
$\mathcal {U}(\mathfrak {g})$. By equation (43), for any ![]() $\mathscr {W}^{k}(\mathfrak {g},f)$-module M, the tensor product
$\mathscr {W}^{k}(\mathfrak {g},f)$-module M, the tensor product ![]() $M{\otimes }L$ has the structure of a
$M{\otimes }L$ has the structure of a ![]() $\mathscr {W}^{k}(\mathfrak {g},f){\otimes } \mathscr {W}^{\ell }(\mathfrak {g})$-module. We are able to describe the decomposition of
$\mathscr {W}^{k}(\mathfrak {g},f){\otimes } \mathscr {W}^{\ell }(\mathfrak {g})$-module. We are able to describe the decomposition of ![]() $M{\otimes }L$ as
$M{\otimes }L$ as ![]() $\mathscr {W}^{k}(\mathfrak {g},f){\otimes } \mathscr {W}^{\ell }(\mathfrak {g})$-modules for various M and L (Theorems 8.1, 8.2, 8.4, 8.7 and Corollaries 8.4, 8.8).
$\mathscr {W}^{k}(\mathfrak {g},f){\otimes } \mathscr {W}^{\ell }(\mathfrak {g})$-modules for various M and L (Theorems 8.1, 8.2, 8.4, 8.7 and Corollaries 8.4, 8.8).
In particular, Corollary 8.4 states that, when M is a generic Verma module of ![]() $\mathscr {W}^{k-1}(\mathfrak {g})$,
$\mathscr {W}^{k-1}(\mathfrak {g})$, ![]() $M{\otimes } L$ decomposes into a direct sum of tensor products of Verma modules of
$M{\otimes } L$ decomposes into a direct sum of tensor products of Verma modules of ![]() $\mathscr {W}^{k}(\mathfrak {g})$ and
$\mathscr {W}^{k}(\mathfrak {g})$ and ![]() $\mathscr {W}^{\ell }(\mathfrak {g})$. In the case that
$\mathscr {W}^{\ell }(\mathfrak {g})$. In the case that ![]() $\mathfrak {g}=\mathfrak {sl}_{2}$ with an appropriate choice of L, this provides the decomposition that was used in [Reference Bershtein, Feigin and LitvinovBFL16] to give a representation theoretic interpretation of the Nakajima–Yoshioka blowup equations for the moduli space of rank two framed torsion-free sheaves on
$\mathfrak {g}=\mathfrak {sl}_{2}$ with an appropriate choice of L, this provides the decomposition that was used in [Reference Bershtein, Feigin and LitvinovBFL16] to give a representation theoretic interpretation of the Nakajima–Yoshioka blowup equations for the moduli space of rank two framed torsion-free sheaves on ![]() $\mathbb {CP}^{2}$. In a forthcoming paper, we show how the decomposition for
$\mathbb {CP}^{2}$. In a forthcoming paper, we show how the decomposition for ![]() $\mathfrak {g}=\mathfrak {sl}_{n}$ stated in Corollary 8.4 can be used to give a representation theoretic interpretation of Nakajima–Yoshioka blowup equations for the moduli space of framed rank n sheaves on
$\mathfrak {g}=\mathfrak {sl}_{n}$ stated in Corollary 8.4 can be used to give a representation theoretic interpretation of Nakajima–Yoshioka blowup equations for the moduli space of framed rank n sheaves on ![]() $\mathbb {CP}^{2}$ via the AGT conjecture established by Schiffmann and Vasserot [Reference Schiffmann and VasserotSV13].
$\mathbb {CP}^{2}$ via the AGT conjecture established by Schiffmann and Vasserot [Reference Schiffmann and VasserotSV13].
1.4 Higher-rank Urod algebras and  $\operatorname {VOA}[M_{4}]$
$\operatorname {VOA}[M_{4}]$
The Urod algebra is proposed to be important for general smooth 4-manifolds. This appeared in the recent work [Reference Feigin and GukovFG18] of Gukov and the third named author. For a compact simply laced Lie group G, one can conjecturally [Reference Feigin and GukovFG18] associate a vertex operator algebra ![]() $\operatorname {VOA}[M] =\operatorname {VOA}[M, G]$ to every smooth 4-manifold M and an category of modules for
$\operatorname {VOA}[M] =\operatorname {VOA}[M, G]$ to every smooth 4-manifold M and an category of modules for ![]() $\operatorname {VOA}[M]$ to every boundary component of M. The vertex algebra
$\operatorname {VOA}[M]$ to every boundary component of M. The vertex algebra ![]() $\operatorname {VOA}[M]$ should then act on the cohomology of the moduli space of G-instantons on M. Moreover, the invariant
$\operatorname {VOA}[M]$ should then act on the cohomology of the moduli space of G-instantons on M. Moreover, the invariant ![]() $\operatorname {VOA}[M]$ should have the following property: Glueing
$\operatorname {VOA}[M]$ should have the following property: Glueing ![]() $4$-manifolds along a common boundary amounts to extending the tensor product of the two associated vertex algebras along the categories of modules; see [Reference Creutzig, Kanade and McRaeCKM19] for the theory of these vertex algebra extensions.
$4$-manifolds along a common boundary amounts to extending the tensor product of the two associated vertex algebras along the categories of modules; see [Reference Creutzig, Kanade and McRaeCKM19] for the theory of these vertex algebra extensions.
When ![]() $G=SU(2)$ we have [Reference Feigin and GukovFG18] that
$G=SU(2)$ we have [Reference Feigin and GukovFG18] that
where ![]() $M_{4}\# \overline {\mathbb {CP}^{2}}$ is the connected sum of
$M_{4}\# \overline {\mathbb {CP}^{2}}$ is the connected sum of ![]() $M_{4}$ and
$M_{4}$ and ![]() $\overline {\mathbb {C} \mathbb {P}^{2}}$. One expects the same type of formula for any simply laced G with
$\overline {\mathbb {C} \mathbb {P}^{2}}$. One expects the same type of formula for any simply laced G with ![]() $\mathcal {U}(\mathfrak {sl}_{2})$ replaced by the corresponding higher-rank Urod algebra.
$\mathcal {U}(\mathfrak {sl}_{2})$ replaced by the corresponding higher-rank Urod algebra.
1.5 Higher-rank Urod algebras and vertex algebras for S-duality
The present work was originally motivated by a conjecture that appeared in the context of vertex algebras for S-duality [Reference Creutzig and GaiottoCG17] .
The problem lives inside four-dimensional supersymmetric GL-twisted gauge theories and vertex algebras appear on the intersection of three-dimensional topological boundary conditions. Such vertex algebras are typically constructed out of W-algebras and affine vertex algebras associated to the Lie algebra ![]() $\mathfrak {g}$ of the gauge group G, and the coupling constant
$\mathfrak {g}$ of the gauge group G, and the coupling constant ![]() $\Psi $ relates to the level shifted by the dual Coxeter number
$\Psi $ relates to the level shifted by the dual Coxeter number ![]() $h^{\vee }$. Different boundary conditions can be concanated to yield other boundary conditions and corresponding vertex algebras are related via vertex algebra extensions. Most of [Reference Creutzig and GaiottoCG17] is dealing with simply laced
$h^{\vee }$. Different boundary conditions can be concanated to yield other boundary conditions and corresponding vertex algebras are related via vertex algebra extensions. Most of [Reference Creutzig and GaiottoCG17] is dealing with simply laced ![]() $\mathfrak {g}$, and the discussion at the bottom of page 22 of [Reference Creutzig and GaiottoCG17] is concerned with the concatenation of boundary conditions called
$\mathfrak {g}$, and the discussion at the bottom of page 22 of [Reference Creutzig and GaiottoCG17] is concerned with the concatenation of boundary conditions called ![]() $B_{1, 0}, B_{-1, 1}$ and
$B_{1, 0}, B_{-1, 1}$ and ![]() $B_{0, 1}$. The main expectation is that the resulting corner vertex algebra coincides with the corner vertex algebra between the boundary conditions
$B_{0, 1}$. The main expectation is that the resulting corner vertex algebra coincides with the corner vertex algebra between the boundary conditions ![]() $B_{1, 0}$ and
$B_{1, 0}$ and ![]() $B_{0, 1}$ dressed by extra decoupled degrees of freedom corresponding to
$B_{0, 1}$ dressed by extra decoupled degrees of freedom corresponding to ![]() $\mathbb {L}_{1}(\mathfrak {g})$. In vertex algebra language, this expectation is precisely the statement of Theorem 8.1 with
$\mathbb {L}_{1}(\mathfrak {g})$. In vertex algebra language, this expectation is precisely the statement of Theorem 8.1 with ![]() $\mu =0=\nu $.
$\mu =0=\nu $.
There are further conjectures around vertex algebras and S-duality. These are mainly the construction of junction or corner vertex algebras which are typically large extensions of products of two vertex algebras associated to ![]() $\mathfrak {g}$. Theorem 9.1, which gives a lattice type construction of vertex operator algebras of CFT type using W-algebras in place of Heisenberg algebras, proves them in a series of cases.
$\mathfrak {g}$. Theorem 9.1, which gives a lattice type construction of vertex operator algebras of CFT type using W-algebras in place of Heisenberg algebras, proves them in a series of cases.
1.6 Rigidity of vertex tensor categories
One of the most difficult problems of the subject of vertex algebras is the understanding of tensor categories of modules of a given vertex algebra. The theory of tensor categories of modules of vertex algebras has been developed in the series of papers [Reference Huang and LepowskyHL94, Reference Huang and LepowskyHL95]. In particular, Yi-Zhi Huang has shown the existence of vertex tensor categories for lisse vertex algebras without the rationality assumption [Reference HuangHua09].
The most challenging technical problem for vertex tensor categories is to prove the rigidity of objects. This is crucial as rigidity gives the categories substantial structure, and many useful theorems only hold for rigid tensor categories. While this problem was settled by Huang for rational, lisse vertex algebras [Reference HuangHua08], it is wide open for nonrational lisse vertex algebras.
In fact, it is expected that the tensor categories of modules should exist for much more general vertex algebras. Strong evidence was given in [Reference Creutzig, Huang and YangCHY18] that showed the category of ordinary modules over an admissible affine vertex algebra associated with a simply laced Lie algebra has the structure of a vertex tensor category.
We conjecture that the category of ordinary modules over a quasi-lisse vertex algebra [Reference Arakawa and KawasetsuAK18] has the structure of a vertex tensor category (Conjecture 1). Note that an admissible affine vertex algebra is quasi-lisse.
Assuming this conjecture and using an idea of [Reference CreutzigCre19], we use the decomposition stated in Theorem 8.1 to prove that certain categories of quasi-lisse W-algebras at admissible level are fusion (Theorem 10.4). Since the conjecture is valid for lisse W-algebras, this gives strong evidence for the rationality conjecture [Reference Kac and WakimotoKW08, Reference ArakawaAra15a] of lisse W-algebras at admissible levels, which has been settled only in some special cases [Reference ArakawaAra15b, Reference Arakawa and van EkerenAvE].
It seems that the translation functor is a good tool to prove rationality of vertex operator algebras in suitable cases. We will explain in forthcoming work how to employ the translation functor in order to get new rational ![]() $\mathscr {W}$-algebras at nonadmissible levels associated to Deligne’s exceptional series [Reference Arakawa, Creutzig and KawasetsuACK].
$\mathscr {W}$-algebras at nonadmissible levels associated to Deligne’s exceptional series [Reference Arakawa, Creutzig and KawasetsuACK].
2 A construction of automorphisms of vertex algebras
Let V be a vertex algebra. As usual, we set ![]() $a_{(n)}=\operatorname {Res}_{z=0}z^{n} a(z)$ for
$a_{(n)}=\operatorname {Res}_{z=0}z^{n} a(z)$ for ![]() $a\in V$, where
$a\in V$, where ![]() $a(z)$ is the quantum field corresponding to a. We have
$a(z)$ is the quantum field corresponding to a. We have
 $$ \begin{align} [a_{(m)},b_{(n)}]=\sum_{j\geqslant 0}\begin{pmatrix} m\\ j\end{pmatrix}(a_{(j)}b)_{(m+n-j)} \end{align} $$
$$ \begin{align} [a_{(m)},b_{(n)}]=\sum_{j\geqslant 0}\begin{pmatrix} m\\ j\end{pmatrix}(a_{(j)}b)_{(m+n-j)} \end{align} $$for ![]() $a,b\in V$,
$a,b\in V$, ![]() $m,n\in \mathbb {Z}$. In particular,
$m,n\in \mathbb {Z}$. In particular, ![]() $[a_{(0)},b_{(n)}]=(a_{(0)}b)_{(n)}$.
$[a_{(0)},b_{(n)}]=(a_{(0)}b)_{(n)}$.
Let A be an element of V such that its zero mode ![]() $A_{(0)}$ acts semisimply on V so that
$A_{(0)}$ acts semisimply on V so that ![]() $V=\bigoplus _{\lambda \in \mathbb {C} }V[\lambda ]$, where
$V=\bigoplus _{\lambda \in \mathbb {C} }V[\lambda ]$, where ![]() $V[\lambda ]=\{v\in V\mid A_{(0)}v=\lambda v\}$. We assume that
$V[\lambda ]=\{v\in V\mid A_{(0)}v=\lambda v\}$. We assume that ![]() $A\in V[0]$. Set
$A\in V[0]$. Set ![]() $V[\geqslant \lambda ]=\bigoplus \limits _{\mu \in \lambda +\mathbb {R}_{\geqslant 0}} {V[\mu ]\supset V[> \lambda ]}=\bigoplus \limits _{\mu > \lambda } V[\mu ]$.
$V[\geqslant \lambda ]=\bigoplus \limits _{\mu \in \lambda +\mathbb {R}_{\geqslant 0}} {V[\mu ]\supset V[> \lambda ]}=\bigoplus \limits _{\mu > \lambda } V[\mu ]$.
Suppose that there exists another element ![]() $\hat {A}\in V[\geqslant 0]$ such that
$\hat {A}\in V[\geqslant 0]$ such that ![]() $\hat {A}\equiv A \pmod {V[>0]}$ and
$\hat {A}\equiv A \pmod {V[>0]}$ and ![]() $\hat {A}_{(0)}$ acts locally finitely on V. Then,
$\hat {A}_{(0)}$ acts locally finitely on V. Then, ![]() $\hat {A}_{(0)}$ acts semisimply on V, and for
$\hat {A}_{(0)}$ acts semisimply on V, and for ![]() $v\in V[\lambda ]$, there exists a unique eigenvector
$v\in V[\lambda ]$, there exists a unique eigenvector ![]() $\tilde {v}$ of
$\tilde {v}$ of ![]() $\hat {A}_{(0)}$ eigenvalue
$\hat {A}_{(0)}$ eigenvalue ![]() $\lambda $ such that
$\lambda $ such that ![]() $\tilde {v}\equiv v\pmod {V[>\lambda ]}$. By extending this correspondence linearly, we obtain a linear map
$\tilde {v}\equiv v\pmod {V[>\lambda ]}$. By extending this correspondence linearly, we obtain a linear map
Lemma 2.1. The map (9) is an automorphism of V.
Proof. Clearly, equation (9) is a linear isomorphism. We wish to show that equation (9) is a homomorphism of vertex algebras. It is clear that ![]() $\widetilde {|0{\rangle }}=|0{\rangle }$. Let
$\widetilde {|0{\rangle }}=|0{\rangle }$. Let ![]() $v\in V[\lambda ]$,
$v\in V[\lambda ]$, ![]() $w\in V[\mu ]$,
$w\in V[\mu ]$, ![]() $n\in \mathbb {Z}$. By equation (8),
$n\in \mathbb {Z}$. By equation (8), ![]() $\tilde {v}_{(n)}\tilde {w}$ is an eigenvector of
$\tilde {v}_{(n)}\tilde {w}$ is an eigenvector of ![]() $\tilde {A}_{(0)}$ of eigenvalue
$\tilde {A}_{(0)}$ of eigenvalue ![]() $\lambda +\mu $ and
$\lambda +\mu $ and ![]() $\tilde {v}_{(n)}\tilde {w}\equiv v_{(n)}w\pmod {V[>\lambda +\mu ]}$. Therefore,
$\tilde {v}_{(n)}\tilde {w}\equiv v_{(n)}w\pmod {V[>\lambda +\mu ]}$. Therefore, ![]() $\tilde {v}_{(n)}\tilde {w}=\widetilde {v_{(n)}w}$. Similarly,
$\tilde {v}_{(n)}\tilde {w}=\widetilde {v_{(n)}w}$. Similarly, ![]() $T\tilde {v}$ is an eigenvector of
$T\tilde {v}$ is an eigenvector of ![]() $\tilde {A}_{(0)}$ of eigenvalue
$\tilde {A}_{(0)}$ of eigenvalue ![]() $\lambda $ such that
$\lambda $ such that ![]() $T\tilde {v}\equiv Tv \pmod {V[>\lambda ]}$. Hence,
$T\tilde {v}\equiv Tv \pmod {V[>\lambda ]}$. Hence, ![]() $T\tilde {v}=\widetilde {Tv}$. This completes the proof.
$T\tilde {v}=\widetilde {Tv}$. This completes the proof.
We also have the following.
Lemma 2.2. The action of ![]() $\hat {A}_{(0)}$ on V coincides with that of
$\hat {A}_{(0)}$ on V coincides with that of ![]() $\tilde {A}_{(0)}$.
$\tilde {A}_{(0)}$.
Proof. For an eigenvector ![]() $v\in V[\geqslant \lambda ]$ of
$v\in V[\geqslant \lambda ]$ of ![]() $\hat {A}_{(0)}$ of eigenvalue
$\hat {A}_{(0)}$ of eigenvalue ![]() $\lambda $,
$\lambda $, ![]() $(\hat {A}_{(0)}-\tilde {A}_{(0)})v$ is also an eigenvector of
$(\hat {A}_{(0)}-\tilde {A}_{(0)})v$ is also an eigenvector of ![]() $\hat {A}_{(0)}$ of eigenvalue
$\hat {A}_{(0)}$ of eigenvalue ![]() $\lambda $. On the other hand,
$\lambda $. On the other hand, ![]() $(\hat {A}_{(0)}-\tilde {A}_{(0)})v$ belongs to
$(\hat {A}_{(0)}-\tilde {A}_{(0)})v$ belongs to ![]() $V[>\lambda ]$. Since all eigenvalues of
$V[>\lambda ]$. Since all eigenvalues of ![]() $\hat {A}_{(0)}$ on
$\hat {A}_{(0)}$ on ![]() $V[>\lambda ]$ are greater than
$V[>\lambda ]$ are greater than ![]() $\lambda $, the vector
$\lambda $, the vector ![]() $(\hat {A}_{(0)}-\tilde {A}_{(0)})v$ must be zero. This completes the proof.
$(\hat {A}_{(0)}-\tilde {A}_{(0)})v$ must be zero. This completes the proof.
Let M be a V-module on which both ![]() $A_{(0)}$ and
$A_{(0)}$ and ![]() $\hat {A}_{(0)}$ act semisimply. Set
$\hat {A}_{(0)}$ act semisimply. Set ![]() $M[\lambda ]=\{m\in M\mid A_{(0)}m=\lambda m\}$,
$M[\lambda ]=\{m\in M\mid A_{(0)}m=\lambda m\}$, ![]() $M[>\lambda ]=\sum _{\mu >\lambda }M[\mu ]$. We can define a linear isomorphism
$M[>\lambda ]=\sum _{\mu >\lambda }M[\mu ]$. We can define a linear isomorphism
that sends ![]() $m\in M[\lambda ]$ to a unique eigenvector
$m\in M[\lambda ]$ to a unique eigenvector ![]() $\tilde {m}$ of
$\tilde {m}$ of ![]() $\hat {A}_{(0)}$ of eigenvalue
$\hat {A}_{(0)}$ of eigenvalue ![]() $\lambda $ such that
$\lambda $ such that ![]() $\tilde {m}\equiv m\pmod {M[>\lambda ]}$. The following assertion can be shown in the same manner as Lemma 2.1.
$\tilde {m}\equiv m\pmod {M[>\lambda ]}$. The following assertion can be shown in the same manner as Lemma 2.1.
Lemma 2.3. We have ![]() $\widetilde {a_{(n)}m}=\tilde {a}_{(n)}\tilde {m}$ for
$\widetilde {a_{(n)}m}=\tilde {a}_{(n)}\tilde {m}$ for ![]() $a\in V$,
$a\in V$, ![]() $m\in M$,
$m\in M$, ![]() $n\in \mathbb {Z}$, that is, (10) is an isomorphism of V-modules.
$n\in \mathbb {Z}$, that is, (10) is an isomorphism of V-modules.
3 Preliminaries on Drinfeld–Sokolov reduction
Let ![]() $\mathfrak {g}$ be a simple Lie algebra over
$\mathfrak {g}$ be a simple Lie algebra over ![]() $\mathbb {C}$, and let
$\mathbb {C}$, and let ![]() $V^{k}(\mathfrak {g})$ be the universal affine vertex algebra associated with
$V^{k}(\mathfrak {g})$ be the universal affine vertex algebra associated with ![]() $\mathfrak {g}$ at level k as in the introduction. A
$\mathfrak {g}$ at level k as in the introduction. A ![]() $V^{k}(\mathfrak {g})$-module is the same as a smooth module M of level k over the affine Kac–Moody algebra
$V^{k}(\mathfrak {g})$-module is the same as a smooth module M of level k over the affine Kac–Moody algebra ![]() $\widehat {\mathfrak {g}}$. Here, a
$\widehat {\mathfrak {g}}$. Here, a ![]() $\widehat {\mathfrak {g}}$-module M is called smooth if
$\widehat {\mathfrak {g}}$-module M is called smooth if ![]() $x(z)=\sum _{n\in \mathbb {Z}}(xt^{n})z^{-n-1}$ is a (quantum) field on M for all
$x(z)=\sum _{n\in \mathbb {Z}}(xt^{n})z^{-n-1}$ is a (quantum) field on M for all ![]() $x\in \mathfrak {g}$, that is,
$x\in \mathfrak {g}$, that is, ![]() $(xt^{n})m=0$ for a sufficiently large n for any
$(xt^{n})m=0$ for a sufficiently large n for any ![]() $m\in M$.
$m\in M$.
Let f be a nilpotent element of ![]() $\mathfrak {g}$. Let
$\mathfrak {g}$. Let
 $$ \begin{align} \mathfrak{g}=\bigoplus_{j\in \frac{1}{2}\mathbb{Z}}\mathfrak{g}_{j} \end{align} $$
$$ \begin{align} \mathfrak{g}=\bigoplus_{j\in \frac{1}{2}\mathbb{Z}}\mathfrak{g}_{j} \end{align} $$be a good grading ([Reference Kac, Roan and WakimotoKRW03]) of ![]() $\mathfrak {g}$ for f, that is,
$\mathfrak {g}$ for f, that is, ![]() $f\in \mathfrak {g}_{-1}$,
$f\in \mathfrak {g}_{-1}$, ![]() $\operatorname {\mathrm {ad}} f:\mathfrak {g}_{j}\rightarrow \mathfrak {g}_{j-1}$ is injective for
$\operatorname {\mathrm {ad}} f:\mathfrak {g}_{j}\rightarrow \mathfrak {g}_{j-1}$ is injective for ![]() $j\geqslant 1/2$ and surjective for
$j\geqslant 1/2$ and surjective for ![]() $j\leqslant 1/2$. Denote by
$j\leqslant 1/2$. Denote by ![]() $x_{0}$ the semisimple element of
$x_{0}$ the semisimple element of ![]() $\mathfrak {g}$ that defines the grading, i.e.,
$\mathfrak {g}$ that defines the grading, i.e.,
We write ![]() $\deg x=d$ if
$\deg x=d$ if ![]() $x\in \mathfrak {g}_{d}$.
$x\in \mathfrak {g}_{d}$.
Let ![]() $\{e,h,f\}$ be an
$\{e,h,f\}$ be an ![]() $\mathfrak {sl}_{2}$-triple associated with f in
$\mathfrak {sl}_{2}$-triple associated with f in ![]() $\mathfrak {g}$. Then the grading defined by
$\mathfrak {g}$. Then the grading defined by ![]() $x_{0}=1/2h$ is good and is called a Dynkin grading.
$x_{0}=1/2h$ is good and is called a Dynkin grading.
Fix a Cartan subalgebra ![]() $\mathfrak {h}$ of
$\mathfrak {h}$ of ![]() $\mathfrak {g}$ that is contained in the Lie subalgebra
$\mathfrak {g}$ that is contained in the Lie subalgebra ![]() $\mathfrak {g}_{0}$. Let
$\mathfrak {g}_{0}$. Let ![]() $\Delta $ be the set of roots of
$\Delta $ be the set of roots of ![]() $\mathfrak {g}$,
$\mathfrak {g}$, ![]() $\mathfrak {g}=\mathfrak {h}\mathop {\oplus } \bigoplus _{\alpha \in \Delta }\mathfrak {g}_{\alpha }$ the root space decomposition. Set
$\mathfrak {g}=\mathfrak {h}\mathop {\oplus } \bigoplus _{\alpha \in \Delta }\mathfrak {g}_{\alpha }$ the root space decomposition. Set ![]() $\Delta _{j}=\{\alpha \in \Delta \mid \mathfrak {g}_{\alpha }\subset \mathfrak {g}_{j}\}$ so that
$\Delta _{j}=\{\alpha \in \Delta \mid \mathfrak {g}_{\alpha }\subset \mathfrak {g}_{j}\}$ so that ![]() $\Delta =\bigsqcup _{j\in \frac {1}{2}\mathbb {Z}}\Delta _{j}$. Put
$\Delta =\bigsqcup _{j\in \frac {1}{2}\mathbb {Z}}\Delta _{j}$. Put ![]() $\Delta _{>0}=\bigsqcup _{j>0}\Delta _{j}$. Let
$\Delta _{>0}=\bigsqcup _{j>0}\Delta _{j}$. Let ![]() $I=\{1,2,\dots , \operatorname {rk}\mathfrak {g}\}$, and let
$I=\{1,2,\dots , \operatorname {rk}\mathfrak {g}\}$, and let ![]() $\{x_{a}\mid a\in I\sqcup \Delta \}$ be a basis of
$\{x_{a}\mid a\in I\sqcup \Delta \}$ be a basis of ![]() $\mathfrak {g}$ such that
$\mathfrak {g}$ such that ![]() $x_{\alpha }\in \mathfrak {g}_{\alpha }$,
$x_{\alpha }\in \mathfrak {g}_{\alpha }$, ![]() $\alpha \in \Delta $, and
$\alpha \in \Delta $, and ![]() $x_{i}\in \mathfrak {h}$,
$x_{i}\in \mathfrak {h}$, ![]() $i\in I$. Denote by
$i\in I$. Denote by ![]() $c_{a b}^{d}$ the corresponding structure constant.
$c_{a b}^{d}$ the corresponding structure constant.
Set ![]() $\mathfrak {g}_{\geqslant 1}=\bigoplus _{j\geqslant 1}\mathfrak {g}_{j}$,
$\mathfrak {g}_{\geqslant 1}=\bigoplus _{j\geqslant 1}\mathfrak {g}_{j}$, ![]() $\mathfrak {g}_{>0}=\bigoplus _{j\geqslant 1/2}\mathfrak {g}_{j}$, and let
$\mathfrak {g}_{>0}=\bigoplus _{j\geqslant 1/2}\mathfrak {g}_{j}$, and let ![]() $\chi :\mathfrak {g}_{\geqslant 1}\rightarrow \mathbb {C}$ be the character defined by
$\chi :\mathfrak {g}_{\geqslant 1}\rightarrow \mathbb {C}$ be the character defined by ![]() $\chi (x)=(f|x)$. We extend
$\chi (x)=(f|x)$. We extend ![]() $\chi $ to the character
$\chi $ to the character ![]() $\hat {\chi }$ of
$\hat {\chi }$ of ![]() $\mathfrak {g}_{\geqslant 1}[t,t^{-1}]$ by setting
$\mathfrak {g}_{\geqslant 1}[t,t^{-1}]$ by setting ![]() $\hat \chi (xt^{n})= \delta _{n,-1}\chi (x)$. Define
$\hat \chi (xt^{n})= \delta _{n,-1}\chi (x)$. Define
where ![]() $\mathbb {C}_{\hat \chi }$ is the one-dimensional representation of
$\mathbb {C}_{\hat \chi }$ is the one-dimensional representation of ![]() $\mathfrak {g}_{>0}[t]+\mathfrak {g}_{\geqslant 1}[t,t^{-1}]$ on which
$\mathfrak {g}_{>0}[t]+\mathfrak {g}_{\geqslant 1}[t,t^{-1}]$ on which ![]() $\mathfrak {g}_{\geqslant 1}[t,t^{-1}]$ acts by the character
$\mathfrak {g}_{\geqslant 1}[t,t^{-1}]$ acts by the character ![]() $\hat \chi $ and
$\hat \chi $ and ![]() $\mathfrak {g}_{>0}[t]$ acts trivially. Since it is a smooth
$\mathfrak {g}_{>0}[t]$ acts trivially. Since it is a smooth ![]() $\mathfrak {g}_{>0}[t,t^{-1}]$-module, the space
$\mathfrak {g}_{>0}[t,t^{-1}]$-module, the space ![]() $F_{\chi }$ is a module over the vertex subalgebra
$F_{\chi }$ is a module over the vertex subalgebra ![]() $V(\mathfrak {g}_{>0 })\subset V^{k}(\mathfrak {g})$ generated by
$V(\mathfrak {g}_{>0 })\subset V^{k}(\mathfrak {g})$ generated by ![]() $x_{\alpha }(z)$ with
$x_{\alpha }(z)$ with ![]() $\alpha \in \Delta _{>0}$. For
$\alpha \in \Delta _{>0}$. For ![]() $\alpha \in \Delta _{> 0}$, let
$\alpha \in \Delta _{> 0}$, let ![]() $\Phi _{\alpha }(z)$ denote the image of
$\Phi _{\alpha }(z)$ denote the image of ![]() $x_{\alpha }(z)$ in
$x_{\alpha }(z)$ in ![]() $(\operatorname {\mathrm {End}} F_{\chi })[[z,z^{-1}]]$. Then
$(\operatorname {\mathrm {End}} F_{\chi })[[z,z^{-1}]]$. Then
and
There is a unique vertex algebra structure on ![]() $F_{\chi }$ such that
$F_{\chi }$ such that ![]() $|0{\rangle }=1{\otimes } 1$ is the vacuum vector and
$|0{\rangle }=1{\otimes } 1$ is the vacuum vector and
for ![]() $\alpha \in \Delta _{>0}$. (Note that
$\alpha \in \Delta _{>0}$. (Note that ![]() $(\Phi _{\alpha })_{(-1)}|0{\rangle }=\chi (x_{\alpha })|0{\rangle } $ for
$(\Phi _{\alpha })_{(-1)}|0{\rangle }=\chi (x_{\alpha })|0{\rangle } $ for ![]() $\alpha \in \Delta _{\geqslant 1}$.) In other words,
$\alpha \in \Delta _{\geqslant 1}$.) In other words, ![]() $F_{\chi }$ has the structure of the
$F_{\chi }$ has the structure of the ![]() $\beta \gamma $-system associated with the symplectic vector space
$\beta \gamma $-system associated with the symplectic vector space ![]() $\mathfrak {g}_{1/2}$ with the symplectic form
$\mathfrak {g}_{1/2}$ with the symplectic form
Next, let ![]() $\bigwedge ^{\infty /2+\bullet }(\mathfrak {g}_{>0})$ be the vertex superalgebra generated by odd fields
$\bigwedge ^{\infty /2+\bullet }(\mathfrak {g}_{>0})$ be the vertex superalgebra generated by odd fields ![]() $\psi _{\alpha }(z)$,
$\psi _{\alpha }(z)$, ![]() $\psi _{\alpha }^{*}(z)$,
$\psi _{\alpha }^{*}(z)$, ![]() $\alpha \in \Delta _{>0}$, with the OPEs
$\alpha \in \Delta _{>0}$, with the OPEs
Let ![]() $\bigwedge ^{\infty /2+\bullet }(\mathfrak {g}_{>0})=\bigoplus _{n\in \mathbb {Z}} \bigwedge ^{\infty /2+n}(\mathfrak {g}_{>0})$ be the
$\bigwedge ^{\infty /2+\bullet }(\mathfrak {g}_{>0})=\bigoplus _{n\in \mathbb {Z}} \bigwedge ^{\infty /2+n}(\mathfrak {g}_{>0})$ be the ![]() $\mathbb {Z}$-gradation defined by
$\mathbb {Z}$-gradation defined by ![]() $\deg |0{\rangle } =0$,
$\deg |0{\rangle } =0$, ![]() $\deg (\psi _{\alpha })_{(n)}=-1$,
$\deg (\psi _{\alpha })_{(n)}=-1$, ![]() $\deg (\psi _{\alpha }^{*})_{(n)}=1$.
$\deg (\psi _{\alpha }^{*})_{(n)}=1$.
For a smooth ![]() $\widehat {\mathfrak {g}}$-module M, set
$\widehat {\mathfrak {g}}$-module M, set
Then ![]() $C(M)=\bigoplus \limits _{i\in \mathbb {Z}}C^{i}(M)$,
$C(M)=\bigoplus \limits _{i\in \mathbb {Z}}C^{i}(M)$, ![]() $C^{i}(M)=M{\otimes } F_{\chi }{\otimes } \bigwedge \nolimits ^{\infty /2+i}(\mathfrak {g}_{>0})$. Note that
$C^{i}(M)=M{\otimes } F_{\chi }{\otimes } \bigwedge \nolimits ^{\infty /2+i}(\mathfrak {g}_{>0})$. Note that ![]() $C(V^{k}(\mathfrak {g}))$ is naturally a vertex superalgebra, and
$C(V^{k}(\mathfrak {g}))$ is naturally a vertex superalgebra, and ![]() $C(M)$ is a module over the vertex superalgebra
$C(M)$ is a module over the vertex superalgebra ![]() $C(V^{k}(\mathfrak {g}))$ for any smooth
$C(V^{k}(\mathfrak {g}))$ for any smooth ![]() $\widehat {\mathfrak {g}}$-module M. Define
$\widehat {\mathfrak {g}}$-module M. Define
 $$ \begin{align*} Q(z)=\sum_{\alpha\in \Delta_{>0}}x_{\alpha}(z)\psi_{\alpha}^{*}(z) +\sum_{\alpha\in \Delta_{>0}}\Phi_{\alpha}(z)\psi_{\alpha}^{*}(z) -\frac{1}{2} \sum_{\alpha,\beta,\gamma\in \Delta_{>0}}c_{\alpha,\beta}^{\gamma} \psi_{\alpha}^{*}(z)\psi_{\beta}^{*}(z)\psi_{\gamma}(z), \end{align*} $$
$$ \begin{align*} Q(z)=\sum_{\alpha\in \Delta_{>0}}x_{\alpha}(z)\psi_{\alpha}^{*}(z) +\sum_{\alpha\in \Delta_{>0}}\Phi_{\alpha}(z)\psi_{\alpha}^{*}(z) -\frac{1}{2} \sum_{\alpha,\beta,\gamma\in \Delta_{>0}}c_{\alpha,\beta}^{\gamma} \psi_{\alpha}^{*}(z)\psi_{\beta}^{*}(z)\psi_{\gamma}(z), \end{align*} $$where we have omitted the tensor product symbol. Then ![]() $Q(z)Q(w)\sim 0$, and we have
$Q(z)Q(w)\sim 0$, and we have ![]() $Q_{(0)}^{2}=0$ on any
$Q_{(0)}^{2}=0$ on any ![]() $C(V^{k}(\mathfrak {g}))$-module. The cohomology
$C(V^{k}(\mathfrak {g}))$-module. The cohomology
is called the BRST cohomologyof the Drinfeld–Sokolov reduction associated with f with coefficients in M ([Reference Feigin and FrenkelFF90a, Reference Kac, Roan and WakimotoKRW03]; see also [Reference ArakawaAra05]). By definition [Reference FeĭginFeĭ84], ![]() $H^{\bullet }_{DS,f}(M)$ is the semi-infinite
$H^{\bullet }_{DS,f}(M)$ is the semi-infinite ![]() $\mathfrak {g}_{>0}[t,t^{-1}]$-cohomology
$\mathfrak {g}_{>0}[t,t^{-1}]$-cohomology ![]() $H^{\frac {\infty }{2}+\bullet }(\mathfrak {g}_{>0}[t,t^{-1}],M\otimes F_{\chi })$ with coefficients in the diagonal
$H^{\frac {\infty }{2}+\bullet }(\mathfrak {g}_{>0}[t,t^{-1}],M\otimes F_{\chi })$ with coefficients in the diagonal ![]() $\mathfrak {g}_{>0}[t,t^{-1}]$-module
$\mathfrak {g}_{>0}[t,t^{-1}]$-module ![]() $M\otimes F_{\chi }$.
$M\otimes F_{\chi }$.
The vertex algebra
is called the W-algebra associated with ![]() $(\mathfrak {g},f)$ at level k, which is conformal provided that
$(\mathfrak {g},f)$ at level k, which is conformal provided that ![]() $k\ne -h^{\vee }$. The vertex algebra structure of
$k\ne -h^{\vee }$. The vertex algebra structure of ![]() $\mathscr {W}^{k}(\mathfrak {g},f)$ does not depend on the choice of a good grading ([Reference Arakawa, Kuwabara and MalikovAKM15]); however, its conformal structure does. The central charge of
$\mathscr {W}^{k}(\mathfrak {g},f)$ does not depend on the choice of a good grading ([Reference Arakawa, Kuwabara and MalikovAKM15]); however, its conformal structure does. The central charge of ![]() $\mathscr {W}^{k}(\mathfrak {g},f)$ is given by
$\mathscr {W}^{k}(\mathfrak {g},f)$ is given by
where ![]() $\rho $ is the half sum of positive roots of
$\rho $ is the half sum of positive roots of ![]() $\mathfrak {g}$.
$\mathfrak {g}$.
Let ![]() $\mathscr {W}_{k}(\mathfrak {g},f)$ be the unique simple graded quotient of
$\mathscr {W}_{k}(\mathfrak {g},f)$ be the unique simple graded quotient of ![]() $\mathscr {W}^{k}(\mathfrak {g},f)$.
$\mathscr {W}^{k}(\mathfrak {g},f)$.
Let ![]() $\operatorname {KL}$ be the full subcategory of
$\operatorname {KL}$ be the full subcategory of ![]() $\widehat {\mathfrak {g}}$-modules consisting of objects on which
$\widehat {\mathfrak {g}}$-modules consisting of objects on which ![]() $\mathfrak {g}$ acts semisimply and
$\mathfrak {g}$ acts semisimply and ![]() $t\mathfrak {g}[t]$ acts locally nilpotently, and let
$t\mathfrak {g}[t]$ acts locally nilpotently, and let ![]() $\operatorname {KL}_{k}$ be the full subcategory of
$\operatorname {KL}_{k}$ be the full subcategory of ![]() $\operatorname {KL}$ consisting of modules of level k.
$\operatorname {KL}$ consisting of modules of level k.
Let Q be the root lattice of ![]() $\mathfrak {g}$,
$\mathfrak {g}$, ![]() $\check {Q}$ the coroot lattice, P the weight lattice,
$\check {Q}$ the coroot lattice, P the weight lattice, ![]() $\check {P}$ the coweight lattice,
$\check {P}$ the coweight lattice, ![]() $P_{+}$ the set of dominant integral weights and
$P_{+}$ the set of dominant integral weights and ![]() $\check {P}_{+}$ the set of dominant integral coweights of
$\check {P}_{+}$ the set of dominant integral coweights of ![]() $\mathfrak {g}$. For
$\mathfrak {g}$. For ![]() $\lambda \in P_{+}$, set
$\lambda \in P_{+}$, set
where ![]() $E_{\lambda }$ is the irreducible finite-dimensional
$E_{\lambda }$ is the irreducible finite-dimensional ![]() $\mathfrak {g}$-module of highest weight
$\mathfrak {g}$-module of highest weight ![]() $\lambda $ lifted to a
$\lambda $ lifted to a ![]() $\mathfrak {g}[t]$-module by letting
$\mathfrak {g}[t]$-module by letting ![]() $\mathfrak {g}[t]t$ act trivially and K by multiplication with the scalar k. Note that
$\mathfrak {g}[t]t$ act trivially and K by multiplication with the scalar k. Note that ![]() $V^{k}(\mathfrak {g})=\mathbb {V}^{k}_{0}$ as a
$V^{k}(\mathfrak {g})=\mathbb {V}^{k}_{0}$ as a ![]() $\widehat {\mathfrak {g}}$-module. We denote by
$\widehat {\mathfrak {g}}$-module. We denote by ![]() $\mathbb {L}^{k}_{\lambda }$ the unique simple graded quotient of
$\mathbb {L}^{k}_{\lambda }$ the unique simple graded quotient of ![]() $\mathbb {V}^{k}_{\lambda }$. More generally, for any weight
$\mathbb {V}^{k}_{\lambda }$. More generally, for any weight ![]() $\lambda $ of
$\lambda $ of ![]() $\mathfrak {g}$, we denote by
$\mathfrak {g}$, we denote by ![]() $\mathbb {L}^{k}_{\lambda }$ the irreducible highest weight representation of
$\mathbb {L}^{k}_{\lambda }$ the irreducible highest weight representation of ![]() $\widehat {\mathfrak {g}}$ with highest weight
$\widehat {\mathfrak {g}}$ with highest weight ![]() $\lambda $ and level k.
$\lambda $ and level k.
Theorem 3.1 [Reference Frenkel and GaitsgoryFG10, Reference ArakawaAra15a]
We have ![]() $H_{DS,f}^{i}(M)=0$ for
$H_{DS,f}^{i}(M)=0$ for ![]() $i\ne 0$ and
$i\ne 0$ and ![]() $M\in \operatorname {KL}_{k}$. In particular, the functor
$M\in \operatorname {KL}_{k}$. In particular, the functor
is exact.
Note that for ![]() $M\in \operatorname {KL}_{k}, N\in \operatorname {KL}_{\ell }$, we have
$M\in \operatorname {KL}_{k}, N\in \operatorname {KL}_{\ell }$, we have ![]() $M{\otimes }N\in \operatorname {KL}_{k+\ell }$. Therefore,
$M{\otimes }N\in \operatorname {KL}_{k+\ell }$. Therefore, ![]() $H^{i}_{DS,f}(M{\otimes } N)=0$ for
$H^{i}_{DS,f}(M{\otimes } N)=0$ for ![]() $i\ne 0$. In particular,
$i\ne 0$. In particular, ![]() $H^{i}_{DS,f}(M{\otimes } L)=0$ for
$H^{i}_{DS,f}(M{\otimes } L)=0$ for ![]() $i\ne 0$ if
$i\ne 0$ if ![]() $M\in \operatorname {KL}$ and L is an integrable representation of
$M\in \operatorname {KL}$ and L is an integrable representation of ![]() $\widehat {\mathfrak {g}}$.
$\widehat {\mathfrak {g}}$.
4 Proof of Theorem 1
Let ![]() $k\in \mathbb {C}$,
$k\in \mathbb {C}$, ![]() $\ell \in \mathbb {Z}_{\geqslant 0}$, and set
$\ell \in \mathbb {Z}_{\geqslant 0}$, and set
For ![]() $t\in \mathbb {C}$, define the element
$t\in \mathbb {C}$, define the element ![]() $Q_{t}\in C$ by
$Q_{t}\in C$ by
 $$ \begin{align} Q_{t}(z)=& \sum_{\alpha\in \Delta_{>0}}(\pi_{1}(x_{\alpha})(z)+t^{2\alpha(x_{0})}\pi_{2}(x_{\alpha})(z))\psi_{\alpha}^{*}(z)\\ & +\sum_{\alpha\in \Delta_{>0}}\Phi_{\alpha}(z)\psi_{\alpha}^{*}(z) -\frac{1}{2} \sum_{\alpha,\beta,\gamma\in \Delta_{>0}}c_{\alpha,\beta}^{\gamma} \psi_{\alpha}^{*}(z)\psi_{\beta}^{*}(z)\psi_{\gamma}(z), \nonumber \end{align} $$
$$ \begin{align} Q_{t}(z)=& \sum_{\alpha\in \Delta_{>0}}(\pi_{1}(x_{\alpha})(z)+t^{2\alpha(x_{0})}\pi_{2}(x_{\alpha})(z))\psi_{\alpha}^{*}(z)\\ & +\sum_{\alpha\in \Delta_{>0}}\Phi_{\alpha}(z)\psi_{\alpha}^{*}(z) -\frac{1}{2} \sum_{\alpha,\beta,\gamma\in \Delta_{>0}}c_{\alpha,\beta}^{\gamma} \psi_{\alpha}^{*}(z)\psi_{\beta}^{*}(z)\psi_{\gamma}(z), \nonumber \end{align} $$where ![]() $\pi _{1}(x_{a})(z)$ (resp.
$\pi _{1}(x_{a})(z)$ (resp. ![]() $\pi _{2}(x_{a})(z)$) denotes the action of
$\pi _{2}(x_{a})(z)$) denotes the action of ![]() $x_{a}(z)$,
$x_{a}(z)$, ![]() $a\in I\sqcup \Delta $, on
$a\in I\sqcup \Delta $, on ![]() $V^{k}(\mathfrak {g})$ (resp. on
$V^{k}(\mathfrak {g})$ (resp. on ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$). Then
$\mathbb {L}_{\ell }(\mathfrak {g})$). Then ![]() $Q_{t}(z)Q_{t}(w)\sim 0$, and therefore,
$Q_{t}(z)Q_{t}(w)\sim 0$, and therefore, ![]() $(Q_{t})_{(0)}^{2}=0$. It follows that
$(Q_{t})_{(0)}^{2}=0$. It follows that ![]() $(C,(Q_{t})_{(0)})$ is a differential graded vertex algebra, and the corresponding cohomology
$(C,(Q_{t})_{(0)})$ is a differential graded vertex algebra, and the corresponding cohomology ![]() $H^{\bullet }(C,(Q_{t})_{(0)})$ is naturally a vertex algebra. Clearly,
$H^{\bullet }(C,(Q_{t})_{(0)})$ is naturally a vertex algebra. Clearly,
see Theorem 3.1.
By [Reference ArakawaAra05, 3.7], the differential ![]() $(Q_{t})_{(0)}$ decomposes as
$(Q_{t})_{(0)}$ decomposes as
where
 $$ \begin{align} \nonumber &d_{t}^{st}=\sum_{\alpha\in \Delta_{>0}}\sum_{n\in \mathbb{Z}}(\pi_{1}(x_{\alpha})_{(n)}+t^{2\alpha(x_{0})}\pi_{2}(x_{\alpha})_{(n)})\psi_{\alpha,(-n)}^{*}\\ &\qquad\qquad\quad+\sum_{\alpha\in \Delta_{1/2}}\sum_{n< 0}\Phi_{\alpha,(n)}\psi^{*}_{\alpha,(-n)} \end{align} $$
$$ \begin{align} \nonumber &d_{t}^{st}=\sum_{\alpha\in \Delta_{>0}}\sum_{n\in \mathbb{Z}}(\pi_{1}(x_{\alpha})_{(n)}+t^{2\alpha(x_{0})}\pi_{2}(x_{\alpha})_{(n)})\psi_{\alpha,(-n)}^{*}\\ &\qquad\qquad\quad+\sum_{\alpha\in \Delta_{1/2}}\sum_{n< 0}\Phi_{\alpha,(n)}\psi^{*}_{\alpha,(-n)} \end{align} $$ $$ \begin{align} &\qquad \qquad \quad -\frac{1}{2} \sum_{\alpha,\beta,\gamma\in \Delta_{>0}}c_{\alpha,\beta}^{\gamma} \sum_{m,n\in \mathbb{Z}} \psi_{\alpha,(m)}^{*}\psi_{\beta,(n)}^{*}\psi_{\gamma,(-m-n)}, \nonumber \\ &d^{\chi}=\sum_{\alpha\in \Delta_{1/2}}\sum_{n\geqslant 0}\Phi_{\alpha,(n)}\psi^{*}_{\alpha,(-n)} +\sum_{\alpha\in \Delta_{1}}\chi(x_{\alpha})\psi^{*}_{\alpha,(0)}, \end{align} $$
$$ \begin{align} &\qquad \qquad \quad -\frac{1}{2} \sum_{\alpha,\beta,\gamma\in \Delta_{>0}}c_{\alpha,\beta}^{\gamma} \sum_{m,n\in \mathbb{Z}} \psi_{\alpha,(m)}^{*}\psi_{\beta,(n)}^{*}\psi_{\gamma,(-m-n)}, \nonumber \\ &d^{\chi}=\sum_{\alpha\in \Delta_{1/2}}\sum_{n\geqslant 0}\Phi_{\alpha,(n)}\psi^{*}_{\alpha,(-n)} +\sum_{\alpha\in \Delta_{1}}\chi(x_{\alpha})\psi^{*}_{\alpha,(0)}, \end{align} $$and ![]() $\{x,y\}=xy+yx$.
$\{x,y\}=xy+yx$.
Define the Hamiltonian H on C by
where ![]() $H_{standard}^{V^{k}(\mathfrak {g})}$ is the standard Hamiltonian of
$H_{standard}^{V^{k}(\mathfrak {g})}$ is the standard Hamiltonian of ![]() $V^{k}(\mathfrak {g})$ that gives
$V^{k}(\mathfrak {g})$ that gives ![]() $\pi _{1}(x)$,
$\pi _{1}(x)$, ![]() $x \in \mathfrak {g}$, conformal weight one and
$x \in \mathfrak {g}$, conformal weight one and ![]() $\omega _{\mathbb {L}_{\ell }(\mathfrak {g})}$ is the Sugawara conformal vector of
$\omega _{\mathbb {L}_{\ell }(\mathfrak {g})}$ is the Sugawara conformal vector of ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$,
$\mathbb {L}_{\ell }(\mathfrak {g})$,
 $$ \begin{align*} &\omega_{F_{\chi}}(z)=\frac{1}{2}\sum\limits_{\alpha\in \Delta_{1/2}}:\partial_{z}\Phi^{\alpha}(z) \Phi_{\alpha}(z):,\\ &\omega_{\bigwedge\nolimits^{\infty/2+\bullet}(\mathfrak{g}_{>0})}(z)= \sum_{j>0}\sum_{\alpha\in \Delta_{j}}j:\psi_{\alpha}^{*}(z)\partial \psi_{\alpha}(z): +\sum_{j>0}\sum_{\alpha\in \Delta_{j}}(1-j):(\partial \psi_{\alpha}^{*}(z))\psi_{\alpha}(z):. \end{align*} $$
$$ \begin{align*} &\omega_{F_{\chi}}(z)=\frac{1}{2}\sum\limits_{\alpha\in \Delta_{1/2}}:\partial_{z}\Phi^{\alpha}(z) \Phi_{\alpha}(z):,\\ &\omega_{\bigwedge\nolimits^{\infty/2+\bullet}(\mathfrak{g}_{>0})}(z)= \sum_{j>0}\sum_{\alpha\in \Delta_{j}}j:\psi_{\alpha}^{*}(z)\partial \psi_{\alpha}(z): +\sum_{j>0}\sum_{\alpha\in \Delta_{j}}(1-j):(\partial \psi_{\alpha}^{*}(z))\psi_{\alpha}(z):. \end{align*} $$Here, ![]() $\{\Phi ^{\alpha }\}$ is a dual basis to
$\{\Phi ^{\alpha }\}$ is a dual basis to ![]() $\{\Phi _{\alpha }\}$, that is,
$\{\Phi _{\alpha }\}$, that is, ![]() $\Phi ^{\alpha }(z)\Phi _{\beta }(w)\sim \delta _{\alpha \beta }/(z-w)$. Then
$\Phi ^{\alpha }(z)\Phi _{\beta }(w)\sim \delta _{\alpha \beta }/(z-w)$. Then ![]() $[H, d_{t}^{st}]=0=[H,d_{t}^{\chi }]$, and thus, H defines a Hamiltonian on the vertex algebra
$[H, d_{t}^{st}]=0=[H,d_{t}^{\chi }]$, and thus, H defines a Hamiltonian on the vertex algebra ![]() $H^{\bullet }(C,(Q_{t})_{(0)})$.
$H^{\bullet }(C,(Q_{t})_{(0)})$.
Following [Reference Frenkel and Ben-ZviFBZ04, Reference Kac, Roan and WakimotoKRW03], define
 $$ \begin{align*} J^{a}(z)={\pi}_{1}(x_{a})(z)+\sum_{\beta,\gamma\in \Delta_{+}}c_{a,\beta}^{\gamma} :\psi_{\gamma}(z)\psi_{\beta}^{*}(z): \end{align*} $$
$$ \begin{align*} J^{a}(z)={\pi}_{1}(x_{a})(z)+\sum_{\beta,\gamma\in \Delta_{+}}c_{a,\beta}^{\gamma} :\psi_{\gamma}(z)\psi_{\beta}^{*}(z): \end{align*} $$for ![]() $a\in I\sqcup \Delta $. We also denote by
$a\in I\sqcup \Delta $. We also denote by ![]() $J^{x}$ the linear combination of
$J^{x}$ the linear combination of ![]() $J^{a}$,
$J^{a}$, ![]() $a\in I\sqcup \Delta _{\leqslant 0}$, corresponding to
$a\in I\sqcup \Delta _{\leqslant 0}$, corresponding to ![]() $x\in \mathfrak {g}_{\leqslant 0}:=\bigoplus _{j\leqslant 0}\mathfrak {g}_{j}$. Let
$x\in \mathfrak {g}_{\leqslant 0}:=\bigoplus _{j\leqslant 0}\mathfrak {g}_{j}$. Let ![]() $C_{\leqslant 0}$ be the vertex subalgebra of C generated by
$C_{\leqslant 0}$ be the vertex subalgebra of C generated by ![]() $J^{x}(z$) (
$J^{x}(z$) (![]() $x\in \mathfrak {g}_{\leqslant 0}$),
$x\in \mathfrak {g}_{\leqslant 0}$), ![]() $\pi _{2}(x)(z)$ (
$\pi _{2}(x)(z)$ (![]() $x\in \mathfrak {g}$),
$x\in \mathfrak {g}$), ![]() $\psi ^{*}_{\alpha }(z)$ (
$\psi ^{*}_{\alpha }(z)$ (![]() $\alpha \in \Delta _{>0}$) and
$\alpha \in \Delta _{>0}$) and ![]() $\Phi _{\alpha }(z)$ (
$\Phi _{\alpha }(z)$ (![]() $\alpha \in \Delta _{1/2}$), and let
$\alpha \in \Delta _{1/2}$), and let ![]() $C_{> 0}$ be the vertex subalgebra of C generated by
$C_{> 0}$ be the vertex subalgebra of C generated by ![]() $\psi _{\alpha }(z)$ and
$\psi _{\alpha }(z)$ and
(![]() $\alpha \in \Delta _{>0}$).
$\alpha \in \Delta _{>0}$).
As in [Reference Frenkel and Ben-ZviFBZ04, Reference Kac, Roan and WakimotoKRW03], we find that both ![]() $C_{\leqslant 0}$ and
$C_{\leqslant 0}$ and ![]() $C_{> 0}$ are subcomplexes of
$C_{> 0}$ are subcomplexes of ![]() $(C, (Q_{t})_{(0)})$ and that
$(C, (Q_{t})_{(0)})$ and that ![]() $C\cong C_{\leqslant 0}{\otimes } C_{>0}$ as complexes. Moreover, we have
$C\cong C_{\leqslant 0}{\otimes } C_{>0}$ as complexes. Moreover, we have
 $$ \begin{align*}H^{i}(C_{>0},(Q_{t})_{(0)})=\begin{cases}\mathbb{C}&\text{for }i= 0\\ 0&\text{for }i\ne 0,\end{cases}\end{align*} $$
$$ \begin{align*}H^{i}(C_{>0},(Q_{t})_{(0)})=\begin{cases}\mathbb{C}&\text{for }i= 0\\ 0&\text{for }i\ne 0,\end{cases}\end{align*} $$and therefore,
as vertex algebras. Since the cohomological gradation takes only nonnegative values on ![]() $C_{\leqslant 0}$, it follows that
$C_{\leqslant 0}$, it follows that ![]() $H^{0}(C,(Q_{t})_{(0)})= H^{0}(C_{\leqslant 0},(Q_{t})_{(0)})$ is a vertex subalgebra of
$H^{0}(C,(Q_{t})_{(0)})= H^{0}(C_{\leqslant 0},(Q_{t})_{(0)})$ is a vertex subalgebra of ![]() $C_{\leqslant 0}$.
$C_{\leqslant 0}$.
Note that the vertex algebra ![]() $C_{\leqslant 0}$ does not depend on the parameter
$C_{\leqslant 0}$ does not depend on the parameter ![]() $t\in \mathbb {C}$. Also,
$t\in \mathbb {C}$. Also, ![]() $C_{\leqslant 0}$ is preserved by the action of both
$C_{\leqslant 0}$ is preserved by the action of both ![]() $d_{t}^{st}$ and
$d_{t}^{st}$ and ![]() $d^{\chi }$.
$d^{\chi }$.
Let ![]() $C_{\leqslant 0,\Delta }=C_{\leqslant 0}\cap C_{\Delta }$ so that
$C_{\leqslant 0,\Delta }=C_{\leqslant 0}\cap C_{\Delta }$ so that ![]() $C_{\leqslant 0}=\bigoplus _{\Delta }C_{\leqslant 0,\Delta }$.
$C_{\leqslant 0}=\bigoplus _{\Delta }C_{\leqslant 0,\Delta }$.
Lemma 4.1. For each ![]() $\Delta $,
$\Delta $, ![]() $C_{\leqslant 0,\Delta }$ is a finite-dimensional subcomplex of
$C_{\leqslant 0,\Delta }$ is a finite-dimensional subcomplex of ![]() $C_{\leqslant 0}$.
$C_{\leqslant 0}$.
Proof. The generators ![]() $J^{x}(z)$ (
$J^{x}(z)$ (![]() $x\in \mathfrak {g}_{\leqslant 0}$),
$x\in \mathfrak {g}_{\leqslant 0}$), ![]() $\psi ^{*}_{\alpha }(z)$ (
$\psi ^{*}_{\alpha }(z)$ (![]() $\alpha \in \Delta _{>0}$) and
$\alpha \in \Delta _{>0}$) and ![]() $\Phi _{\alpha }(z)$ (
$\Phi _{\alpha }(z)$ (![]() $\alpha \in \Delta _{1/2}$) have positive conformal weights with respect to the Hamiltonian H. Therefore, it is sufficient to show that the vertex subalgebra
$\alpha \in \Delta _{1/2}$) have positive conformal weights with respect to the Hamiltonian H. Therefore, it is sufficient to show that the vertex subalgebra ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$ that is generated by
$\mathbb {L}_{\ell }(\mathfrak {g})$ that is generated by ![]() $\pi _{2}(x)(z)$,
$\pi _{2}(x)(z)$, ![]() $x\in \mathfrak {g}$, has finite-dimensional weight spaces
$x\in \mathfrak {g}$, has finite-dimensional weight spaces ![]() $\mathbb {L}_{\ell }(\mathfrak {g})_{\Delta }:=\mathbb {L}_{\ell }(\mathfrak {g})\cap C_{\leqslant 0,\Delta }$ and the conformal weights of
$\mathbb {L}_{\ell }(\mathfrak {g})_{\Delta }:=\mathbb {L}_{\ell }(\mathfrak {g})\cap C_{\leqslant 0,\Delta }$ and the conformal weights of ![]() $L_{\ell }(\mathfrak {g})$ is bounded from the above. On the other hand, the action of H on
$L_{\ell }(\mathfrak {g})$ is bounded from the above. On the other hand, the action of H on ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$ is the same as the twisted action of
$\mathbb {L}_{\ell }(\mathfrak {g})$ is the same as the twisted action of ![]() $(\omega _{\mathbb {L}_{\ell }(\mathfrak {g})})_{(1)}$ corresponding to Li’s delta operator associated with
$(\omega _{\mathbb {L}_{\ell }(\mathfrak {g})})_{(1)}$ corresponding to Li’s delta operator associated with ![]() $-x_{0}$. Since
$-x_{0}$. Since ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$ is rational and lisse, the conformal weights of this twisted representation are bounded from above and the weight spaces are finite-dimensional. This completes the proof.
$\mathbb {L}_{\ell }(\mathfrak {g})$ is rational and lisse, the conformal weights of this twisted representation are bounded from above and the weight spaces are finite-dimensional. This completes the proof.
Since both ![]() $d_{t}^{st}$ and
$d_{t}^{st}$ and ![]() $d^{\chi }$ preserve
$d^{\chi }$ preserve ![]() $C_{\leqslant 0,\Delta }$, we can consider the spectral sequence
$C_{\leqslant 0,\Delta }$, we can consider the spectral sequence ![]() $E_{r}\Rightarrow H^{\bullet }(C_{\leqslant 0})$ such that
$E_{r}\Rightarrow H^{\bullet }(C_{\leqslant 0})$ such that ![]() $d_{0}=d^{\chi }$ and
$d_{0}=d^{\chi }$ and ![]() $d_{1}=d_{t}^{st}$, which is converging since each
$d_{1}=d_{t}^{st}$, which is converging since each ![]() $C_{\leqslant 0,\Delta }$ is finite dimensional. As in [Reference Frenkel and Ben-ZviFBZ04, Reference Kac and WakimotoKW04, Reference Kac and WakimotoKW05], we find that
$C_{\leqslant 0,\Delta }$ is finite dimensional. As in [Reference Frenkel and Ben-ZviFBZ04, Reference Kac and WakimotoKW04, Reference Kac and WakimotoKW05], we find that
where ![]() $V^{k^{\natural }}(\mathfrak {g}^{f})$ is the vertex subalgebra of
$V^{k^{\natural }}(\mathfrak {g}^{f})$ is the vertex subalgebra of ![]() $C_{\leqslant 0}$ generated by
$C_{\leqslant 0}$ generated by ![]() $J^{x}(z)$,
$J^{x}(z)$, ![]() $x\in \mathfrak {g}^{f}$. Thus, the spectral sequence collapses at
$x\in \mathfrak {g}^{f}$. Thus, the spectral sequence collapses at ![]() $E_{1}=E_{\infty }$, and we get the vertex algebra isomorphism
$E_{1}=E_{\infty }$, and we get the vertex algebra isomorphism
Here, ![]() $\operatorname {\mathrm {gr}} H^{q}(C_{t,\leqslant 0})$ is the associated graded vertex algebra with respect to the filtration that defines the spectral sequence. By equation (24), for each
$\operatorname {\mathrm {gr}} H^{q}(C_{t,\leqslant 0})$ is the associated graded vertex algebra with respect to the filtration that defines the spectral sequence. By equation (24), for each ![]() $v\in V^{k^{\natural }}(\mathfrak {g}^{f}){\otimes } \mathbb {L}_{\ell }(\mathfrak {g})$, there exists a cocycle
$v\in V^{k^{\natural }}(\mathfrak {g}^{f}){\otimes } \mathbb {L}_{\ell }(\mathfrak {g})$, there exists a cocycle
such that
Set
where we recall that ![]() $x_{0}$ is defined by equation (12). Then
$x_{0}$ is defined by equation (12). Then ![]() $C_{\leqslant 0}=\bigoplus _{\lambda \in \frac {1}{2}\mathbb {Z}}C_{\leqslant 0} [\lambda ]$,
$C_{\leqslant 0}=\bigoplus _{\lambda \in \frac {1}{2}\mathbb {Z}}C_{\leqslant 0} [\lambda ]$, ![]() $C_{\leqslant 0}[\lambda ]=\{c\in C_{\leqslant 0}\mid A_{(0)}c=\lambda c\}$, and
$C_{\leqslant 0}[\lambda ]=\{c\in C_{\leqslant 0}\mid A_{(0)}c=\lambda c\}$, and ![]() $A\in C_{\leqslant 0}[0]$. Consider the corresponding cocycle
$A\in C_{\leqslant 0}[0]$. Consider the corresponding cocycle ![]() $\hat {A}$ that has cohomolological degree zero. Since
$\hat {A}$ that has cohomolological degree zero. Since ![]() $d^{st}_{t}A\subset C_{\leqslant 0}[>0]$ and
$d^{st}_{t}A\subset C_{\leqslant 0}[>0]$ and ![]() $d^{\chi }C_{\leqslant 0}[\lambda ]\subset C_{\leqslant 0}[\lambda ]$, we may assume that
$d^{\chi }C_{\leqslant 0}[\lambda ]\subset C_{\leqslant 0}[\lambda ]$, we may assume that ![]() $\hat {A}\equiv A\pmod {C_{\leqslant 0}[>0]}$. Moreover, we may assume that
$\hat {A}\equiv A\pmod {C_{\leqslant 0}[>0]}$. Moreover, we may assume that ![]() $\hat {A}$ is homogenous with respect to the Hamiltonian H so that
$\hat {A}$ is homogenous with respect to the Hamiltonian H so that ![]() $\hat {A}$ preserves each finite-dimensional subcomplex
$\hat {A}$ preserves each finite-dimensional subcomplex ![]() $C_{\leqslant 0,\Delta }$. In particular,
$C_{\leqslant 0,\Delta }$. In particular, ![]() $\hat {A}$ is locally finite on
$\hat {A}$ is locally finite on ![]() $C_{\leqslant 0}$. Therefore, we can apply the construction of Section 2 to obtain the automorphism
$C_{\leqslant 0}$. Therefore, we can apply the construction of Section 2 to obtain the automorphism
of vertex algebras.
Note that ![]() $\tilde {A}\equiv A\pmod {C[>0]}$ and the operator
$\tilde {A}\equiv A\pmod {C[>0]}$ and the operator ![]() $A_{(0)}$ acts semisimply on the whole complex C so that
$A_{(0)}$ acts semisimply on the whole complex C so that ![]() $C=\bigoplus _{\lambda \in \frac {1}{2}\mathbb {Z}}C[\lambda ]$,
$C=\bigoplus _{\lambda \in \frac {1}{2}\mathbb {Z}}C[\lambda ]$, ![]() $C[\lambda ]=\{c\in C\mid A_{(0)}c=\lambda c\}$. Since
$C[\lambda ]=\{c\in C\mid A_{(0)}c=\lambda c\}$. Since ![]() $\varphi _{t}$ is an automorphism of the vertex algebra,
$\varphi _{t}$ is an automorphism of the vertex algebra, ![]() $\tilde {A}\in \varphi _{t}(\mathbb {L}_{\ell }(\mathfrak {g}))$ generates a Heisenberg vertex subalgebra. In particular,
$\tilde {A}\in \varphi _{t}(\mathbb {L}_{\ell }(\mathfrak {g}))$ generates a Heisenberg vertex subalgebra. In particular, ![]() $\tilde {A}_{(0)}$ acts semisimply on C. Therefore, by replacing
$\tilde {A}_{(0)}$ acts semisimply on C. Therefore, by replacing ![]() $\hat {A}$ by
$\hat {A}$ by ![]() $\tilde {A}$ (see Lemma 2.2), we can extend the automorphism (26) to the automorphism
$\tilde {A}$ (see Lemma 2.2), we can extend the automorphism (26) to the automorphism
which is also denoted by ![]() $\varphi _{t}$.
$\varphi _{t}$.
Proposition 4.2. We have ![]() $\varphi _{t}(Q_{t=0})_{(0)}=( Q_{t})_{(0)}$ on C. In particular,
$\varphi _{t}(Q_{t=0})_{(0)}=( Q_{t})_{(0)}$ on C. In particular, ![]() $\varphi _{t}$ defines an isomorphism
$\varphi _{t}$ defines an isomorphism
of differential graded vertex algebras.
Proof. We first show that ![]() $\varphi _{t}(Q_{t=0})_{(0)}=( Q_{t})_{(0)}$ on
$\varphi _{t}(Q_{t=0})_{(0)}=( Q_{t})_{(0)}$ on ![]() $C_{\leqslant 0}$. Since
$C_{\leqslant 0}$. Since ![]() $\varphi _{t}(Q_{t=0})_{(0)}\tilde {A}=\varphi _{t}(Q_{t=0})_{(0)}\varphi _{t}(A)= \varphi _{t}((Q_{t=0})_{(0)}A)=0 $, we have
$\varphi _{t}(Q_{t=0})_{(0)}\tilde {A}=\varphi _{t}(Q_{t=0})_{(0)}\varphi _{t}(A)= \varphi _{t}((Q_{t=0})_{(0)}A)=0 $, we have ![]() $[\varphi _{t}(Q_{t=0})_{(0)},\tilde {A}_{(0)}]=0$. Also,
$[\varphi _{t}(Q_{t=0})_{(0)},\tilde {A}_{(0)}]=0$. Also, ![]() $[(Q_{t})_{(0)},\tilde {A}_{(0)}]= [(Q_{t})_{(0)},\hat {A}_{(0)}]=0$ on
$[(Q_{t})_{(0)},\tilde {A}_{(0)}]= [(Q_{t})_{(0)},\hat {A}_{(0)}]=0$ on ![]() $C_{\leqslant 0}$ by Lemma 2.2. Let
$C_{\leqslant 0}$ by Lemma 2.2. Let ![]() $c\in C_{\leqslant 0}[\geqslant \lambda ]$ be an eigenvector of
$c\in C_{\leqslant 0}[\geqslant \lambda ]$ be an eigenvector of ![]() $\tilde {A}_{(0)}$ of eigenvalue
$\tilde {A}_{(0)}$ of eigenvalue ![]() $\lambda $. Then the vector
$\lambda $. Then the vector ![]() $(\varphi _{t}(Q_{t=0})_{(0)}-(Q_{t})_{(0)})c$ is also an eigenvector of
$(\varphi _{t}(Q_{t=0})_{(0)}-(Q_{t})_{(0)})c$ is also an eigenvector of ![]() $\tilde {A}_{(0)}$ of eigenvalue
$\tilde {A}_{(0)}$ of eigenvalue ![]() $\lambda $. On the other hand, note that
$\lambda $. On the other hand, note that ![]() $\varphi _{t}(Q_{t=0})\equiv Q_{t=0}\equiv Q_{t=1}\pmod {C_{\leqslant 0}[\geqslant \lambda ]}$. Hence,
$\varphi _{t}(Q_{t=0})\equiv Q_{t=0}\equiv Q_{t=1}\pmod {C_{\leqslant 0}[\geqslant \lambda ]}$. Hence, ![]() $(\varphi _{t}(Q_{t=0})_{(0)}-(Q_{t})_{(0)})c\in C_{\leqslant 0}[>\lambda ]$. Since all the eigenvalues of
$(\varphi _{t}(Q_{t=0})_{(0)}-(Q_{t})_{(0)})c\in C_{\leqslant 0}[>\lambda ]$. Since all the eigenvalues of ![]() $\tilde {A}_{(0)}$ on
$\tilde {A}_{(0)}$ on ![]() $C_{\leqslant 0}[>\lambda ]$ are greater than
$C_{\leqslant 0}[>\lambda ]$ are greater than ![]() $\lambda $, we get that
$\lambda $, we get that ![]() $(\varphi _{t}(Q_{t=0})_{(0)}-(Q_{t})_{(0)})c=0$. Hence,
$(\varphi _{t}(Q_{t=0})_{(0)}-(Q_{t})_{(0)})c=0$. Hence, ![]() $\varphi _{t}(Q_{t=0})_{(0)}=(Q_{t})_{(0)}$ on
$\varphi _{t}(Q_{t=0})_{(0)}=(Q_{t})_{(0)}$ on ![]() $C_{\leqslant 0}$.
$C_{\leqslant 0}$.
Next, since ![]() $(Q_{t})_{(0)}\tilde {A}=0$, we have
$(Q_{t})_{(0)}\tilde {A}=0$, we have ![]() $[(Q_{t})_{(0)},\tilde {A}_{(0)}]=0$ on the whole space C. Therefore, we can repeat the same argument for an eigenvector
$[(Q_{t})_{(0)},\tilde {A}_{(0)}]=0$ on the whole space C. Therefore, we can repeat the same argument for an eigenvector ![]() $c\in C[\geqslant \lambda ]$ of
$c\in C[\geqslant \lambda ]$ of ![]() $\tilde {A}_{(0)}$ of eigenvalue
$\tilde {A}_{(0)}$ of eigenvalue ![]() $\lambda $ to obtain that
$\lambda $ to obtain that ![]() $(\varphi _{t}(Q_{t=0})_{(0)}-(Q_{t})_{(0)})c=0$ for all
$(\varphi _{t}(Q_{t=0})_{(0)}-(Q_{t})_{(0)})c=0$ for all ![]() $c\in C$.
$c\in C$.
The last assertion follows since ![]() $\varphi _{t}$ preserves the cohomological gradation as
$\varphi _{t}$ preserves the cohomological gradation as ![]() $\hat {A}$ has cohomological degree zero.
$\hat {A}$ has cohomological degree zero.
By Proposition 4.2, ![]() $\varphi :=\varphi _{t=1}$ defines an isomorphism
$\varphi :=\varphi _{t=1}$ defines an isomorphism
of differential graded vertex algebras. We have shown the following assertion.
Theorem 4.3. The automorphism ![]() $\varphi $ induces an isomorphism
$\varphi $ induces an isomorphism ![]() $H^{\bullet }(C,(Q_{t=0})_{(0)})\cong H^{\bullet }(C,(Q_{t=1})_{(0)})$. In particular,
$H^{\bullet }(C,(Q_{t=0})_{(0)})\cong H^{\bullet }(C,(Q_{t=1})_{(0)})$. In particular,
as vertex algebras.
Proof of Theorem 1 .
Let V be a vertex algebra equipped with a vertex algebra homomorphism ![]() $V^{k}(\mathfrak {g})\rightarrow V$. Since
$V^{k}(\mathfrak {g})\rightarrow V$. Since ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$ is rational, both
$\mathbb {L}_{\ell }(\mathfrak {g})$ is rational, both ![]() $A_{(0)}$ and
$A_{(0)}$ and ![]() $\tilde {A}_{(0)}$ acts semisimply on
$\tilde {A}_{(0)}$ acts semisimply on ![]() $C(V{\otimes } \mathbb {L}_{\ell }(\mathfrak {g}))$. Hence, we can apply Lemma 2.1 to extend
$C(V{\otimes } \mathbb {L}_{\ell }(\mathfrak {g}))$. Hence, we can apply Lemma 2.1 to extend ![]() $\varphi $ to the isomorphism
$\varphi $ to the isomorphism ![]() $C(V{\otimes } \mathbb {L}_{\ell }(\mathfrak {g}), (Q_{t=0})_{(0)})\cong C(V{\otimes } \mathbb {L}_{\ell }(\mathfrak {g}), (Q_{t=t})_{(0)})$ of differential graded vertex algebras, which gives the the isomorphism
$C(V{\otimes } \mathbb {L}_{\ell }(\mathfrak {g}), (Q_{t=0})_{(0)})\cong C(V{\otimes } \mathbb {L}_{\ell }(\mathfrak {g}), (Q_{t=t})_{(0)})$ of differential graded vertex algebras, which gives the the isomorphism ![]() $H_{DS,f}^{\bullet }(V{\otimes } \mathbb {L}_{\ell }(\mathfrak {g}))\cong H_{DS,f}^{\bullet }(V){\otimes } \mathbb {L}_{\ell }(\mathfrak {g})$ of vertex algebras. Similarly, if M is a V-module and N is an
$H_{DS,f}^{\bullet }(V{\otimes } \mathbb {L}_{\ell }(\mathfrak {g}))\cong H_{DS,f}^{\bullet }(V){\otimes } \mathbb {L}_{\ell }(\mathfrak {g})$ of vertex algebras. Similarly, if M is a V-module and N is an ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$-module, it follows from Lemma 2.3 that we have an isomorphism
$\mathbb {L}_{\ell }(\mathfrak {g})$-module, it follows from Lemma 2.3 that we have an isomorphism ![]() $H_{DS,f}^{\bullet }(M{\otimes } N)\cong H_{DS,f}^{\bullet }(M){\otimes } N$ as modules over
$H_{DS,f}^{\bullet }(M{\otimes } N)\cong H_{DS,f}^{\bullet }(M){\otimes } N$ as modules over ![]() $H_{DS,f}^{\bullet }(V{\otimes } \mathbb {L}_{\ell }(\mathfrak {g}))\cong H_{DS,f}^{\bullet }(V){\otimes } \mathbb {L}_{\ell }(\mathfrak {g})$.
$H_{DS,f}^{\bullet }(V{\otimes } \mathbb {L}_{\ell }(\mathfrak {g}))\cong H_{DS,f}^{\bullet }(V){\otimes } \mathbb {L}_{\ell }(\mathfrak {g})$.
Example 4.4. Let ![]() $\mathfrak {g}=\mathfrak {sl}_{2}=\operatorname {span}_{\mathbb {C}}\{e,h,f\}$ and
$\mathfrak {g}=\mathfrak {sl}_{2}=\operatorname {span}_{\mathbb {C}}\{e,h,f\}$ and ![]() $\ell =1$, and consider the Drinfeld–Sokolov reduction associated with f. Then
$\ell =1$, and consider the Drinfeld–Sokolov reduction associated with f. Then ![]() $C=V^{k}(\mathfrak {g}){\otimes } \mathbb {L}_{1}(\mathfrak {g}){\otimes } \bigwedge \nolimits ^{\infty /2+\bullet }(\mathfrak {g}_{>0})$, and
$C=V^{k}(\mathfrak {g}){\otimes } \mathbb {L}_{1}(\mathfrak {g}){\otimes } \bigwedge \nolimits ^{\infty /2+\bullet }(\mathfrak {g}_{>0})$, and ![]() $\bigwedge \nolimits ^{\infty /2+\bullet }(\mathfrak {g}_{>0})$ is generated by odd fields
$\bigwedge \nolimits ^{\infty /2+\bullet }(\mathfrak {g}_{>0})$ is generated by odd fields ![]() $\psi (z)=\psi _{\alpha }(z)$,
$\psi (z)=\psi _{\alpha }(z)$, ![]() $\psi ^{*}(z) =\psi _{\alpha }^{*}(z)$. We have
$\psi ^{*}(z) =\psi _{\alpha }^{*}(z)$. We have
where we have set ![]() $x_{i}=\pi _{i}(x)$ for
$x_{i}=\pi _{i}(x)$ for ![]() $x\in \mathfrak {g}$,
$x\in \mathfrak {g}$, ![]() $i=1,2$. The vertex subalgebra
$i=1,2$. The vertex subalgebra ![]() $C_{\leqslant 0}$ is generated by
$C_{\leqslant 0}$ is generated by ![]() $J^{f_{1}}(z)=f_{1}(z)$,
$J^{f_{1}}(z)=f_{1}(z)$, ![]() $J^{h_{1}}(z)=h_{1}(z)+2:\!\psi (z)\psi ^{*}(z)\!:$,
$J^{h_{1}}(z)=h_{1}(z)+2:\!\psi (z)\psi ^{*}(z)\!:$, ![]() $e_{2}(z)$,
$e_{2}(z)$, ![]() $h_{2}(z)$,
$h_{2}(z)$, ![]() $f_{2}(z)$ and
$f_{2}(z)$ and ![]() $\psi ^{*}(z)$. We have
$\psi ^{*}(z)$. We have ![]() $A=h_{2}/2$, and
$A=h_{2}/2$, and
We find that the isomorphism
is given by
 $$ \begin{align*} &e_{1}(z)\mapsto e_{1}(z)(1-t^{2} e_{2}(z)), \\ &h_{1}(z)\mapsto h_{1}(z)-t^{2} k\partial_{z} e_{2}(z),\\ &f_{1}(z)\mapsto f_{1}(z)(1+t^{2} e_{2}(z)),\\ &e_{2}(z)\mapsto e_{2}(z),\\ &h_{2}(z)\mapsto h_{2}(z)+t^{2}J^{h_{1}}(z)e_{2}(z),\\ &f_{2}(z)\mapsto f_{2}(z) -\frac{t^{2}}{2}J^{h_{1}}(z)h_{2}(z) + \partial_{z}J {}^{h_{1}}(z)-\frac{t^{4}}{4} :\!e_{2}(z) J^{h_{1}}(z)^{2}\!:, \\ &\psi(z)\mapsto \psi(z)(1-t^{2} e_{2}(z)),\\ &\psi^{*}(z)\mapsto \psi^{*}(z)(1+t^{2}e_{2}(z)). \end{align*} $$
$$ \begin{align*} &e_{1}(z)\mapsto e_{1}(z)(1-t^{2} e_{2}(z)), \\ &h_{1}(z)\mapsto h_{1}(z)-t^{2} k\partial_{z} e_{2}(z),\\ &f_{1}(z)\mapsto f_{1}(z)(1+t^{2} e_{2}(z)),\\ &e_{2}(z)\mapsto e_{2}(z),\\ &h_{2}(z)\mapsto h_{2}(z)+t^{2}J^{h_{1}}(z)e_{2}(z),\\ &f_{2}(z)\mapsto f_{2}(z) -\frac{t^{2}}{2}J^{h_{1}}(z)h_{2}(z) + \partial_{z}J {}^{h_{1}}(z)-\frac{t^{4}}{4} :\!e_{2}(z) J^{h_{1}}(z)^{2}\!:, \\ &\psi(z)\mapsto \psi(z)(1-t^{2} e_{2}(z)),\\ &\psi^{*}(z)\mapsto \psi^{*}(z)(1+t^{2}e_{2}(z)). \end{align*} $$Note that we have ![]() $(1-t^{2} e_{2}(z))(1+t^{2} e_{2}(z))=1$ on
$(1-t^{2} e_{2}(z))(1+t^{2} e_{2}(z))=1$ on ![]() $\mathbb {L}_{1}(\mathfrak {g})$.
$\mathbb {L}_{1}(\mathfrak {g})$.
5 Remarks on superalgebras
We restricted our attention to vertex algebras, and here we remark that the results also hold for vertex superalgebras, i.e.,
Remark 5.1. All results of section 2 also hold if we allow V to be a vertex superalgebra such that A and ![]() $\hat {A}$ are even elements of V.
$\hat {A}$ are even elements of V.
Remark 5.2. In the proofs of section 4, we only used the following properties of ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$:
$\mathbb {L}_{\ell }(\mathfrak {g})$:
1. finite dimensionality and boundedness from above of conformal weight spaces of
 $\mathbb {L}_{\ell }(\mathfrak {g})$ with respect to the twisted action of
$\mathbb {L}_{\ell }(\mathfrak {g})$ with respect to the twisted action of  $(\omega _{\mathbb {L}_{\ell }(\mathfrak {g})})_{(1)}$ corresponding to Li’s delta operator associated with
$(\omega _{\mathbb {L}_{\ell }(\mathfrak {g})})_{(1)}$ corresponding to Li’s delta operator associated with  $-x_{0}$ (see the proof of Lemma 4.1);
$-x_{0}$ (see the proof of Lemma 4.1);2. semisimple action of
 $A_{0}$, where
$A_{0}$, where  $A:=\pi _{2}(x_{0})\in \mathbb {L}_{\ell }(\mathfrak {g})$, on
$A:=\pi _{2}(x_{0})\in \mathbb {L}_{\ell }(\mathfrak {g})$, on  $\mathbb {L}_{\ell }(\mathfrak {g})$-modules.
$\mathbb {L}_{\ell }(\mathfrak {g})$-modules.
Thus, the results are also true by replacing ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$ by any vertex algebra that carries an action of
$\mathbb {L}_{\ell }(\mathfrak {g})$ by any vertex algebra that carries an action of ![]() $V^{\ell }(\mathfrak {g})$ and satisfies these two properties. We can also allow
$V^{\ell }(\mathfrak {g})$ and satisfies these two properties. We can also allow ![]() $\mathfrak {g}$ to be a Lie superalgebra and f an even nilpotent element such that
$\mathfrak {g}$ to be a Lie superalgebra and f an even nilpotent element such that ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$ satisfies the above two properties.
$\mathbb {L}_{\ell }(\mathfrak {g})$ satisfies the above two properties.
First, if we take ![]() $\mathfrak {g} = \mathfrak {osp}_{1|2n}$ and a positive integer
$\mathfrak {g} = \mathfrak {osp}_{1|2n}$ and a positive integer ![]() $\ell $, then
$\ell $, then ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$ is rational [Reference Creutzig and LinshawCL21, Thm. 7.1]. Hence, Theorem 1 holds for
$\mathbb {L}_{\ell }(\mathfrak {g})$ is rational [Reference Creutzig and LinshawCL21, Thm. 7.1]. Hence, Theorem 1 holds for ![]() $\mathfrak {g} = \mathfrak {osp}_{1|2n}$.
$\mathfrak {g} = \mathfrak {osp}_{1|2n}$.
Unfortunately, except for the ![]() $\mathfrak {g} = \mathfrak {osp}_{1|2n}$ cases, there are only few integrable representations of
$\mathfrak {g} = \mathfrak {osp}_{1|2n}$ cases, there are only few integrable representations of ![]() $\widehat {\mathfrak {g}}$ [Reference Kac and WakimotoKW94, Theorem 8.1]. For this reason, the notion of principal integrable representations and subprincipal integrable representations of
$\widehat {\mathfrak {g}}$ [Reference Kac and WakimotoKW94, Theorem 8.1]. For this reason, the notion of principal integrable representations and subprincipal integrable representations of ![]() $\widehat {\mathfrak {g}}$ was introduced in [Reference Kac and WakimotoKW01], which are integrable modules with respect to a certain affine vertex subalgebra, call it
$\widehat {\mathfrak {g}}$ was introduced in [Reference Kac and WakimotoKW01], which are integrable modules with respect to a certain affine vertex subalgebra, call it ![]() $\mathbb {L}_{\ell }(\mathfrak a)$, with
$\mathbb {L}_{\ell }(\mathfrak a)$, with ![]() $\mathfrak {a}\subset \mathfrak {g}_{\bar 0}$, where
$\mathfrak {a}\subset \mathfrak {g}_{\bar 0}$, where ![]() $\mathfrak {g}_{\bar 0}$ is the even part of
$\mathfrak {g}_{\bar 0}$ is the even part of ![]() $\mathfrak {g}$.
$\mathfrak {g}$.
Theorem 5.3. Let ![]() $\mathfrak {g}$ be a basic classical Lie superalgebra with
$\mathfrak {g}$ be a basic classical Lie superalgebra with ![]() $\mathfrak {g}_{\bar 0}=\mathfrak {a}\mathop {\oplus } \mathfrak {a^{\prime }}$,
$\mathfrak {g}_{\bar 0}=\mathfrak {a}\mathop {\oplus } \mathfrak {a^{\prime }}$, ![]() $\mathfrak {a}$ semisimple,
$\mathfrak {a}$ semisimple, ![]() $\mathfrak {a}^{\prime }$ reductive. Suppose that
$\mathfrak {a}^{\prime }$ reductive. Suppose that ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$ is integrable as a representation of
$\mathbb {L}_{\ell }(\mathfrak {g})$ is integrable as a representation of ![]() $\widehat {\mathfrak {a}}\subset \widehat {\mathfrak {g}}$, and f is a nilpotent element in
$\widehat {\mathfrak {a}}\subset \widehat {\mathfrak {g}}$, and f is a nilpotent element in ![]() $\mathfrak {a}$. For a quotient V of
$\mathfrak {a}$. For a quotient V of ![]() $V^{k}(\mathfrak {g})$, we have a vertex algebra isomorphism
$V^{k}(\mathfrak {g})$, we have a vertex algebra isomorphism
where in the left-hand side the Drinfeld–Sokolov reduction is taken with respect to the diagonal action of ![]() $\widehat {\mathfrak {g}}$ on
$\widehat {\mathfrak {g}}$ on ![]() $V{\otimes } \mathbb {L}_{\ell }(\mathfrak {g})$. More generally, let V be a vertex algebra equipped with a vertex algebra homomorphism
$V{\otimes } \mathbb {L}_{\ell }(\mathfrak {g})$. More generally, let V be a vertex algebra equipped with a vertex algebra homomorphism ![]() $V^{k}(\mathfrak {g})\rightarrow V$. Then we have an isomorphism
$V^{k}(\mathfrak {g})\rightarrow V$. Then we have an isomorphism
of graded vertex algebras, and for any V-module M, ![]() $ \mathbb {L}_{\ell }(\mathfrak {g})$-module N, there is an isomorphism
$ \mathbb {L}_{\ell }(\mathfrak {g})$-module N, there is an isomorphism
as modules over ![]() $H_{DS,f}^{\bullet }(V\otimes \mathbb {L}_{\ell }(\mathfrak {g}))\cong H_{DS,f}^{\bullet }(V)\otimes \mathbb {L}_{\ell }(\mathfrak {g})$.
$H_{DS,f}^{\bullet }(V\otimes \mathbb {L}_{\ell }(\mathfrak {g}))\cong H_{DS,f}^{\bullet }(V)\otimes \mathbb {L}_{\ell }(\mathfrak {g})$.
Proof. Since ![]() $f\in \mathfrak {a}$, there is an
$f\in \mathfrak {a}$, there is an ![]() $\mathfrak {sl}_{2}$-triple
$\mathfrak {sl}_{2}$-triple ![]() $\{e,h,f\}$ in
$\{e,h,f\}$ in ![]() $\mathfrak {a}$, and we can assume that
$\mathfrak {a}$, and we can assume that ![]() $x=\frac {1}{2}h$.
$x=\frac {1}{2}h$.
Let ![]() $V_{\ell }(\mathfrak {g}_{\bar 0})$ be the vertex subalgebra of
$V_{\ell }(\mathfrak {g}_{\bar 0})$ be the vertex subalgebra of ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$ generated by
$\mathbb {L}_{\ell }(\mathfrak {g})$ generated by ![]() $y\in \mathfrak {g}_{\bar 0}$. We have
$y\in \mathfrak {g}_{\bar 0}$. We have ![]() $V_{\ell }(\mathfrak {g}_{\bar 0})\cong V_{\ell }(\mathfrak {a}){\otimes } V_{\ell }(\mathfrak {a}^{\prime })$, where
$V_{\ell }(\mathfrak {g}_{\bar 0})\cong V_{\ell }(\mathfrak {a}){\otimes } V_{\ell }(\mathfrak {a}^{\prime })$, where ![]() $ V_{\ell }(\mathfrak {a})$ and
$ V_{\ell }(\mathfrak {a})$ and ![]() $V_{\ell }(\mathfrak {a}^{\prime })$ are vertex subalgebras of
$V_{\ell }(\mathfrak {a}^{\prime })$ are vertex subalgebras of ![]() $V_{\ell }(\mathfrak {g}_{\bar 0})$ generated by
$V_{\ell }(\mathfrak {g}_{\bar 0})$ generated by ![]() $y\in \mathfrak {a}$ and
$y\in \mathfrak {a}$ and ![]() $y\in \mathfrak {a}^{\prime }$, respectively. By the assumption,
$y\in \mathfrak {a}^{\prime }$, respectively. By the assumption, ![]() $V_{\ell }(\mathfrak {a})$ is integrable, and hence is rational. It follows that any
$V_{\ell }(\mathfrak {a})$ is integrable, and hence is rational. It follows that any ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$-module is a direct sum of integrable
$\mathbb {L}_{\ell }(\mathfrak {g})$-module is a direct sum of integrable ![]() $\widehat {\mathfrak {a}}$-modules. Thus, the condition (2) is satisfied.
$\widehat {\mathfrak {a}}$-modules. Thus, the condition (2) is satisfied.
To see that the condition (1) is satisfied, let us consider the twisted ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$ -module
$\mathbb {L}_{\ell }(\mathfrak {g})$ -module ![]() $\sigma _{-x_{0}}^{*}\mathbb {L}_{\ell }(\mathfrak {g})$ corresponding to Li’s delta operator associated with
$\sigma _{-x_{0}}^{*}\mathbb {L}_{\ell }(\mathfrak {g})$ corresponding to Li’s delta operator associated with ![]() $-x_{0}$. Since it is irreducible, it is sufficient to show that
$-x_{0}$. Since it is irreducible, it is sufficient to show that ![]() $\sigma _{-x_{0}}^{*}\mathbb {L}_{\ell }(\mathfrak {g})$ is a highest weight representation of
$\sigma _{-x_{0}}^{*}\mathbb {L}_{\ell }(\mathfrak {g})$ is a highest weight representation of ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$. Clearly, any root vector corresponding to an odd root acts locally nilpotently on
$\mathbb {L}_{\ell }(\mathfrak {g})$. Clearly, any root vector corresponding to an odd root acts locally nilpotently on ![]() $\sigma _{-x_{0}}^{*}\mathbb {L}_{\ell }(\mathfrak {g})$. Hence, it suffices to show that any root vector corresponding to a even positive root acts locally nilpotently on
$\sigma _{-x_{0}}^{*}\mathbb {L}_{\ell }(\mathfrak {g})$. Hence, it suffices to show that any root vector corresponding to a even positive root acts locally nilpotently on ![]() $\sigma _{-x_{0}}^{*}\mathbb {L}_{\ell }(\mathfrak {g})$. This is clear for a root corresponding to
$\sigma _{-x_{0}}^{*}\mathbb {L}_{\ell }(\mathfrak {g})$. This is clear for a root corresponding to ![]() $\widehat {\mathfrak {a}^{\prime }}$ as elements of
$\widehat {\mathfrak {a}^{\prime }}$ as elements of ![]() $\mathfrak {a}^{\prime }$ are orthogonal to
$\mathfrak {a}^{\prime }$ are orthogonal to ![]() $x\in \mathfrak {a}$. On the other hand, since
$x\in \mathfrak {a}$. On the other hand, since ![]() $V_{\ell }(\mathfrak {a})$ is integrable,
$V_{\ell }(\mathfrak {a})$ is integrable, ![]() $\sigma _{-x_{0}}^{*}\mathbb {L}_{\ell }(\mathfrak {g})$ is integrable over
$\sigma _{-x_{0}}^{*}\mathbb {L}_{\ell }(\mathfrak {g})$ is integrable over ![]() $V_{\ell }(\mathfrak {a})$. Hence, any root vector corresponding to a even positive root acts locally nilpotently on
$V_{\ell }(\mathfrak {a})$. Hence, any root vector corresponding to a even positive root acts locally nilpotently on ![]() $\sigma _{-x_{0}}^{*}\mathbb {L}_{\ell }(\mathfrak {g})$. This completes the proof.
$\sigma _{-x_{0}}^{*}\mathbb {L}_{\ell }(\mathfrak {g})$. This completes the proof.
6 Urod conformal vector
In this section, we assume that k is not critical, and discuss how the conformal structure match under the isomorphism
of vertex algebras.
On the right-hand side, the conformal vector of ![]() $H_{DS,f}^{0}(V^{k}(\mathfrak {g}){\otimes } \mathbb {L}_{\ell }(\mathfrak {g}))$ is given by
$H_{DS,f}^{0}(V^{k}(\mathfrak {g}){\otimes } \mathbb {L}_{\ell }(\mathfrak {g}))$ is given by
where ![]() $\omega _{V^{k}(\mathfrak {g})}$ is the Sugawara conformal vector of
$\omega _{V^{k}(\mathfrak {g})}$ is the Sugawara conformal vector of ![]() $V^{k}(\mathfrak {g})$. It has the central charge
$V^{k}(\mathfrak {g})$. It has the central charge
 $$ \begin{align} \frac{k\dim \mathfrak{g}}{k+h^{\vee}}& +\frac{\ell\dim \mathfrak{g}}{\ell+h^{\vee}} -\frac{(k+\ell)\dim \mathfrak{g}}{k+\ell+h^{\vee}}\\ &+ \dim \mathfrak{g}_{0}-\frac{1}{2}\dim \mathfrak{g}_{1/2}-12|\frac{\rho}{\sqrt{k +\ell+h^{\vee}}}-\sqrt{k+\ell+h^{\vee}}x_{0}|^{2}. \nonumber \end{align} $$
$$ \begin{align} \frac{k\dim \mathfrak{g}}{k+h^{\vee}}& +\frac{\ell\dim \mathfrak{g}}{\ell+h^{\vee}} -\frac{(k+\ell)\dim \mathfrak{g}}{k+\ell+h^{\vee}}\\ &+ \dim \mathfrak{g}_{0}-\frac{1}{2}\dim \mathfrak{g}_{1/2}-12|\frac{\rho}{\sqrt{k +\ell+h^{\vee}}}-\sqrt{k+\ell+h^{\vee}}x_{0}|^{2}. \nonumber \end{align} $$Clearly, ![]() $\varphi ^{-1}(\omega _{total})$ is a conformal vector of
$\varphi ^{-1}(\omega _{total})$ is a conformal vector of ![]() $\mathscr {W}^{k}(\mathfrak {g},f){\otimes } \mathbb {L}_{\ell }(\mathfrak {g})$. Set
$\mathscr {W}^{k}(\mathfrak {g},f){\otimes } \mathbb {L}_{\ell }(\mathfrak {g})$. Set
where ![]() $\omega _{\mathscr {W}^{k}(\mathfrak {g},f)}$ is the conformal vector of
$\omega _{\mathscr {W}^{k}(\mathfrak {g},f)}$ is the conformal vector of ![]() $\mathscr {W}^{k}(\mathfrak {g},f)$. Since it commutes with
$\mathscr {W}^{k}(\mathfrak {g},f)$. Since it commutes with ![]() $\omega _{\mathscr {W}^{k}(\mathfrak {g},f)}$,
$\omega _{\mathscr {W}^{k}(\mathfrak {g},f)}$, ![]() $\omega _{Urod}$ defines a conformal vector of
$\omega _{Urod}$ defines a conformal vector of ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$ ([Reference Lepowsky and LiLL04, 3.11]), which is called the Urod conformal vector of
$\mathbb {L}_{\ell }(\mathfrak {g})$ ([Reference Lepowsky and LiLL04, 3.11]), which is called the Urod conformal vector of ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$. It depends on the choice of
$\mathbb {L}_{\ell }(\mathfrak {g})$. It depends on the choice of ![]() $x_{0}$ and k and has the central charge
$x_{0}$ and k and has the central charge
 $$ \begin{align} \frac{k\dim \mathfrak{g}}{k+h^{\vee}}& +\frac{\ell\dim \mathfrak{g}}{\ell+h^{\vee}} -\frac{(k+\ell)\dim \mathfrak{g}}{k+\ell+h^{\vee}}\\ + 12&\left(|\frac{\rho}{\sqrt{k +h^{\vee}}}-\sqrt{k+h^{\vee}}x_{0}|^{2} -|\frac{\rho}{\sqrt{k +\ell+h^{\vee}}}-\sqrt{k+\ell+h^{\vee}}x_{0}|^{2}\right). \nonumber \end{align} $$
$$ \begin{align} \frac{k\dim \mathfrak{g}}{k+h^{\vee}}& +\frac{\ell\dim \mathfrak{g}}{\ell+h^{\vee}} -\frac{(k+\ell)\dim \mathfrak{g}}{k+\ell+h^{\vee}}\\ + 12&\left(|\frac{\rho}{\sqrt{k +h^{\vee}}}-\sqrt{k+h^{\vee}}x_{0}|^{2} -|\frac{\rho}{\sqrt{k +\ell+h^{\vee}}}-\sqrt{k+\ell+h^{\vee}}x_{0}|^{2}\right). \nonumber \end{align} $$In the case that ![]() $\mathfrak {g}$ is simply laced and
$\mathfrak {g}$ is simply laced and ![]() $f=f_{prin}$, the central charge (33) becomes
$f=f_{prin}$, the central charge (33) becomes
where h is the Coxeter number, and we have used the strange formula ![]() $|\rho |^{2}/2h^{\vee }=\dim \mathfrak {g}/24$, and so it does not depend on the parameter k.
$|\rho |^{2}/2h^{\vee }=\dim \mathfrak {g}/24$, and so it does not depend on the parameter k.
By definition, the conformal vertex algebra ![]() $\mathscr {W}^{k}(\mathfrak {g},f){\otimes } \mathbb {L}_{\ell }(\mathfrak {g})$ with the conformal vector
$\mathscr {W}^{k}(\mathfrak {g},f){\otimes } \mathbb {L}_{\ell }(\mathfrak {g})$ with the conformal vector ![]() $\omega _{\mathscr {W}^{k}(\mathfrak {g},f)}+\omega _{Urod}$ is isomorphic to
$\omega _{\mathscr {W}^{k}(\mathfrak {g},f)}+\omega _{Urod}$ is isomorphic to ![]() $H_{DS,f}^{0}(V^{k}(\mathfrak {g}){\otimes } \mathbb {L}_{\ell }(\mathfrak {g})) $ as conformal vertex algebras.
$H_{DS,f}^{0}(V^{k}(\mathfrak {g}){\otimes } \mathbb {L}_{\ell }(\mathfrak {g})) $ as conformal vertex algebras.
Lemma 6.1. The Hamiltonian of ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$ defined by
$\mathbb {L}_{\ell }(\mathfrak {g})$ defined by ![]() $\omega _{Urod}$ coincides with
$\omega _{Urod}$ coincides with
Proof. For a homogenous element ![]() $x\in \mathfrak {g}$,
$x\in \mathfrak {g}$, ![]() $\pi _{2}(x)\in C$ has the conformal weight
$\pi _{2}(x)\in C$ has the conformal weight ![]() $1-\deg x$. Hence,
$1-\deg x$. Hence, ![]() $\tilde {x}$ has the the conformal weight
$\tilde {x}$ has the the conformal weight ![]() $1-\deg x$ as well.
$1-\deg x$ as well.
Example 6.2 Continued from Example 4.4
The Urod conformal vector of ![]() $\mathbb {L}_{1}(\mathfrak {g})$ is given by
$\mathbb {L}_{1}(\mathfrak {g})$ is given by
which agrees with [Reference Bershtein, Feigin and LitvinovBFL16].
7 Compatibility with twists
In this section, we show that the various twisted Drinfeld–Sokolov reduction functors commute with tensoring integrable representations as well.
For ![]() ${\check \mu } \in \check {P}$, we define a character
${\check \mu } \in \check {P}$, we define a character ![]() $\hat {\chi }_{\check \mu }$ of
$\hat {\chi }_{\check \mu }$ of ![]() $\mathfrak {g}_{\geqslant 1}[t,t^{-1}]$ by the formula
$\mathfrak {g}_{\geqslant 1}[t,t^{-1}]$ by the formula
Define
where ![]() $\mathbb {C}_{\hat \chi _{{\check \mu }}}$ is the one-dimensional representation of
$\mathbb {C}_{\hat \chi _{{\check \mu }}}$ is the one-dimensional representation of ![]() $\mathfrak {g}_{>0}[t]+\mathfrak {g}_{\geqslant 1}[t,t^{-1}]$ on which
$\mathfrak {g}_{>0}[t]+\mathfrak {g}_{\geqslant 1}[t,t^{-1}]$ on which ![]() $\mathfrak {g}_{\geqslant 1}[t,t^{-1}]$ acts by the character
$\mathfrak {g}_{\geqslant 1}[t,t^{-1}]$ acts by the character ![]() $\hat \chi _{{\check \mu }}$ and
$\hat \chi _{{\check \mu }}$ and ![]() $\mathfrak {g}_{>0}[t]$ acts trivially. Then
$\mathfrak {g}_{>0}[t]$ acts trivially. Then ![]() $F_{\chi ,{\check \mu }}$ is naturally a
$F_{\chi ,{\check \mu }}$ is naturally a ![]() $V(\mathfrak {g}_{>0})$-module, and we denote by
$V(\mathfrak {g}_{>0})$-module, and we denote by ![]() $\Phi _{\alpha }^{{\check \mu }}(z)$ the image of
$\Phi _{\alpha }^{{\check \mu }}(z)$ the image of ![]() $x_{\alpha }(z)$ in
$x_{\alpha }(z)$ in ![]() $(\operatorname {\mathrm {End}} F_{\chi ,{\check \mu }}))[z,z^{-1}]$. We have
$(\operatorname {\mathrm {End}} F_{\chi ,{\check \mu }}))[z,z^{-1}]$. We have
 $$ \begin{align*} &\Phi_{\alpha}^{{\check\mu}}(z)=z^{{\langle} {\check\mu},\alpha{\rangle}}\chi(x_{\alpha}) \quad \text{for }\alpha\in \Delta_{>0},\\ &\Phi_{\alpha}^{{\check\mu}}(z)\Phi_{\beta}^{{\check\mu}}(w)\sim \frac{w^{{\langle} {\check\mu},\alpha+\beta{\rangle}} \chi([x_{\alpha},x_{\beta}])}{z-w.}\end{align*} $$
$$ \begin{align*} &\Phi_{\alpha}^{{\check\mu}}(z)=z^{{\langle} {\check\mu},\alpha{\rangle}}\chi(x_{\alpha}) \quad \text{for }\alpha\in \Delta_{>0},\\ &\Phi_{\alpha}^{{\check\mu}}(z)\Phi_{\beta}^{{\check\mu}}(w)\sim \frac{w^{{\langle} {\check\mu},\alpha+\beta{\rangle}} \chi([x_{\alpha},x_{\beta}])}{z-w.}\end{align*} $$ For a smooth ![]() $\widehat {\mathfrak {g}}$-module M of level k, we define
$\widehat {\mathfrak {g}}$-module M of level k, we define
where ![]() $\mathfrak {g}_{>0}[t,t^{-1}]$ acts diagonally on
$\mathfrak {g}_{>0}[t,t^{-1}]$ acts diagonally on ![]() $M{\otimes } F_{\chi ,{\check \mu }}$. By definition,
$M{\otimes } F_{\chi ,{\check \mu }}$. By definition, ![]() $H_{DS,f,{\check \mu }}^{\bullet }(M)$ is the cohomology of the complex
$H_{DS,f,{\check \mu }}^{\bullet }(M)$ is the cohomology of the complex ![]() $(C_{{\check \mu }}(M), (Q_{{\check \mu }})_{(0)})$, where
$(C_{{\check \mu }}(M), (Q_{{\check \mu }})_{(0)})$, where ![]() $C_{{\check \mu }}(M)=M{\otimes } F_{\chi ,{\check \mu }}{\otimes }\bigwedge \nolimits ^{\infty /2+\bullet }(\mathfrak {g}_{>0}) $ and
$C_{{\check \mu }}(M)=M{\otimes } F_{\chi ,{\check \mu }}{\otimes }\bigwedge \nolimits ^{\infty /2+\bullet }(\mathfrak {g}_{>0}) $ and ![]() $(Q_{{\check \mu }})_{(0)}$ is the zero mode of the field
$(Q_{{\check \mu }})_{(0)}$ is the zero mode of the field
 $$ \begin{align*} Q_{{\check\mu}}(z)=\sum_{\alpha\in \Delta_{>0}}x_{\alpha}(z)\psi_{\alpha}^{*}(z) +\sum_{\alpha\in \Delta_{>0}}\Phi_{\alpha}^{{\check\mu}}(z)\psi_{\alpha}^{*}(z) -\frac{1}{2} \sum_{\alpha,\beta,\gamma\in \Delta_{>0}}c_{\alpha,\beta}^{\gamma} \psi_{\alpha}^{*}(z)\psi_{\beta}^{*}(z)\psi_{\gamma}(z), \end{align*} $$
$$ \begin{align*} Q_{{\check\mu}}(z)=\sum_{\alpha\in \Delta_{>0}}x_{\alpha}(z)\psi_{\alpha}^{*}(z) +\sum_{\alpha\in \Delta_{>0}}\Phi_{\alpha}^{{\check\mu}}(z)\psi_{\alpha}^{*}(z) -\frac{1}{2} \sum_{\alpha,\beta,\gamma\in \Delta_{>0}}c_{\alpha,\beta}^{\gamma} \psi_{\alpha}^{*}(z)\psi_{\beta}^{*}(z)\psi_{\gamma}(z), \end{align*} $$on ![]() $C_{{\check \mu }}(M)$.
$C_{{\check \mu }}(M)$.
We define the structure of a ![]() $\mathscr {W}^{k}(\mathfrak {g},f)$-module on
$\mathscr {W}^{k}(\mathfrak {g},f)$-module on ![]() $H_{DS,f,\check {\mu }}^{i}(M), i \in \mathbb {Z}$, as follows. Let
$H_{DS,f,\check {\mu }}^{i}(M), i \in \mathbb {Z}$, as follows. Let ![]() $\Delta (J^{\{{\check \mu }\}},z)$ be Li’s delta operator corresponding to the field
$\Delta (J^{\{{\check \mu }\}},z)$ be Li’s delta operator corresponding to the field
 $$ \begin{align} J^{\{{\check\mu}\}}(z):={\check\mu}(z) + \sum_{\alpha \in \Delta_{>0}} {\langle} \alpha,{\check\mu} {\rangle} :\! \psi_{\alpha}(z) \psi^{*}_{\alpha}(z) \! : -\frac{1}{2}\sum_{\alpha \in \Delta_{1/2}}{\langle} \alpha,{\check\mu}{\rangle} :\! \Phi_{\alpha}(z) \Phi^{\alpha}(z) \! : \end{align} $$
$$ \begin{align} J^{\{{\check\mu}\}}(z):={\check\mu}(z) + \sum_{\alpha \in \Delta_{>0}} {\langle} \alpha,{\check\mu} {\rangle} :\! \psi_{\alpha}(z) \psi^{*}_{\alpha}(z) \! : -\frac{1}{2}\sum_{\alpha \in \Delta_{1/2}}{\langle} \alpha,{\check\mu}{\rangle} :\! \Phi_{\alpha}(z) \Phi^{\alpha}(z) \! : \end{align} $$in ![]() $C(V^{k}(\mathfrak {g}))$, where
$C(V^{k}(\mathfrak {g}))$, where ![]() $\Phi ^{\alpha }(z)$ is a linear sum of
$\Phi ^{\alpha }(z)$ is a linear sum of ![]() $\Phi ^{\beta }(z)$ corresponding to the vector
$\Phi ^{\beta }(z)$ corresponding to the vector ![]() $x^{\alpha }$ dual to
$x^{\alpha }$ dual to ![]() $x_{\alpha }$ with respect to the symplectic form (13), that is,
$x_{\alpha }$ with respect to the symplectic form (13), that is, ![]() $(f|[x_{\alpha },x^{\beta }])=\delta _{\alpha ,\beta }$. We have
$(f|[x_{\alpha },x^{\beta }])=\delta _{\alpha ,\beta }$. We have
 $$ \begin{align*} J^{\{{\check\mu}\}}(z)x_{\alpha}(w)\sim \frac{{\langle} \alpha,{\check\mu} {\rangle} }{z-w}x_{\alpha}(w), \quad J^{\{{\check\mu}\}}(z)\Phi_{\alpha}(w)\sim \frac{{\langle} \alpha,{\check\mu} {\rangle} }{z-w}\Phi_{\alpha}(w),\\ J^{\{{\check\mu}\}}(z)\psi_{\alpha}(w)\sim \frac{{\langle} \alpha,{\check\mu} {\rangle} }{z-w}\psi_{\alpha}(w), \quad J^{\{{\check\mu}\}}(w)\psi^{*}_{\alpha}(z)\sim -\frac{{\langle} \alpha,{\check\mu} {\rangle} }{z-w}\psi^{*}_{\alpha}(w); \end{align*} $$
$$ \begin{align*} J^{\{{\check\mu}\}}(z)x_{\alpha}(w)\sim \frac{{\langle} \alpha,{\check\mu} {\rangle} }{z-w}x_{\alpha}(w), \quad J^{\{{\check\mu}\}}(z)\Phi_{\alpha}(w)\sim \frac{{\langle} \alpha,{\check\mu} {\rangle} }{z-w}\Phi_{\alpha}(w),\\ J^{\{{\check\mu}\}}(z)\psi_{\alpha}(w)\sim \frac{{\langle} \alpha,{\check\mu} {\rangle} }{z-w}\psi_{\alpha}(w), \quad J^{\{{\check\mu}\}}(w)\psi^{*}_{\alpha}(z)\sim -\frac{{\langle} \alpha,{\check\mu} {\rangle} }{z-w}\psi^{*}_{\alpha}(w); \end{align*} $$see [Reference Kac, Roan and WakimotoKRW03]. For any smooth ![]() $\widehat {\mathfrak {g}}$-module M, we can twist the action of
$\widehat {\mathfrak {g}}$-module M, we can twist the action of ![]() $C(V^{k}(\mathfrak {g}))$ on
$C(V^{k}(\mathfrak {g}))$ on ![]() $C(M)$ by the correspondence
$C(M)$ by the correspondence
for any ![]() $A\in C(V^{\kappa }(\mathfrak {g}))$. Since we have
$A\in C(V^{\kappa }(\mathfrak {g}))$. Since we have
 $$ \begin{align*} & \sigma_{\check\mu}(x_{\alpha}(z))=z^{- {\langle} \alpha,{\check\mu} {\rangle} }x_{\alpha}(z),\quad \sigma_{\check\mu}(\Phi_{\alpha}(z))=z^{- {\langle} \alpha,{\check\mu} {\rangle} }\Phi_{\alpha}(z),\\ & \sigma_{\check\mu}(\psi_{\alpha}(z))=z^{- {\langle} \alpha,{\check\mu} {\rangle} }\psi_{\alpha}(z), \quad \sigma_{\check\mu}(\psi^{*}_{\alpha}(z))=z^{{\langle} \alpha,{\check\mu} {\rangle} }\psi^{*}_{\alpha}(z), \end{align*} $$
$$ \begin{align*} & \sigma_{\check\mu}(x_{\alpha}(z))=z^{- {\langle} \alpha,{\check\mu} {\rangle} }x_{\alpha}(z),\quad \sigma_{\check\mu}(\Phi_{\alpha}(z))=z^{- {\langle} \alpha,{\check\mu} {\rangle} }\Phi_{\alpha}(z),\\ & \sigma_{\check\mu}(\psi_{\alpha}(z))=z^{- {\langle} \alpha,{\check\mu} {\rangle} }\psi_{\alpha}(z), \quad \sigma_{\check\mu}(\psi^{*}_{\alpha}(z))=z^{{\langle} \alpha,{\check\mu} {\rangle} }\psi^{*}_{\alpha}(z), \end{align*} $$it follows that the resulting complex ![]() $(C(M),\sigma _{\check \mu }(Q_{(0)}))$ is naturally identified with
$(C(M),\sigma _{\check \mu }(Q_{(0)}))$ is naturally identified with ![]() $(C_{{\check \mu }}(M), (Q_{{\check \mu }})_{(0)})$. Therefore,
$(C_{{\check \mu }}(M), (Q_{{\check \mu }})_{(0)})$. Therefore, ![]() $(C_{{\check \mu }}(M), (Q_{{\check \mu }})_{(0)})$ has the structure of a differential graded module over the differential vertex algebra
$(C_{{\check \mu }}(M), (Q_{{\check \mu }})_{(0)})$ has the structure of a differential graded module over the differential vertex algebra ![]() $(C(V^{k}(\mathfrak {g})),Q_{(0)}))$, and hence, each cohomology
$(C(V^{k}(\mathfrak {g})),Q_{(0)}))$, and hence, each cohomology ![]() $H_{DS,f,\check {\mu }}^{i}(M), i \in \mathbb {Z}$, is a module over
$H_{DS,f,\check {\mu }}^{i}(M), i \in \mathbb {Z}$, is a module over ![]() $\mathscr {W}^{k}(\mathfrak {g},f)=H_{DS,f}^{0}(M)$.
$\mathscr {W}^{k}(\mathfrak {g},f)=H_{DS,f}^{0}(M)$.
The functor ![]() $H_{DS,f,\check {\mu }}^{0}(?)$ was introduced in [Reference Arakawa and FrenkelAF19] in the case that f is a principal nilpotent element.
$H_{DS,f,\check {\mu }}^{0}(?)$ was introduced in [Reference Arakawa and FrenkelAF19] in the case that f is a principal nilpotent element.
Let V be vertex algebra equipped with a vertex algebra homomorphism ![]() $V^{k}(\mathfrak {g})\rightarrow V$, and let M be a V-module. Then the same construction as above gives
$V^{k}(\mathfrak {g})\rightarrow V$, and let M be a V-module. Then the same construction as above gives ![]() $H_{DS,f,\check {\mu }}^{i}(M)$ a structure of a module over the vertex algebra
$H_{DS,f,\check {\mu }}^{i}(M)$ a structure of a module over the vertex algebra ![]() $H_{DS,f}^{0}(V)$.
$H_{DS,f}^{0}(V)$.
Theorem 7.1. Let V be a quotient of the universal affine vertex algebra ![]() $V^{k}(\mathfrak {g})$,
$V^{k}(\mathfrak {g})$, ![]() $\ell \in \mathbb {Z}_{\geqslant 0}$, and let
$\ell \in \mathbb {Z}_{\geqslant 0}$, and let ![]() ${\check \mu } \in \check {P}$. For any V-module M,
${\check \mu } \in \check {P}$. For any V-module M, ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$-module N and
$\mathbb {L}_{\ell }(\mathfrak {g})$-module N and ![]() $i\in \mathbb {Z}$, there is an isomorphism
$i\in \mathbb {Z}$, there is an isomorphism
as modules over ![]() $H_{DS,f}^{0}(V\otimes \mathbb {L}_{\ell }(\mathfrak {g}))\cong H_{DS,f}^{0}(V)\otimes \mathbb {L}_{\ell }(\mathfrak {g})$, where
$H_{DS,f}^{0}(V\otimes \mathbb {L}_{\ell }(\mathfrak {g}))\cong H_{DS,f}^{0}(V)\otimes \mathbb {L}_{\ell }(\mathfrak {g})$, where ![]() $\sigma _{\check \mu }^{*} N$ is the twist of N on which
$\sigma _{\check \mu }^{*} N$ is the twist of N on which ![]() $A\in \mathbb {L}_{\ell }(\mathfrak {g})$ acts as
$A\in \mathbb {L}_{\ell }(\mathfrak {g})$ acts as ![]() $\sigma _{{\check \mu }}(A(z))$.
$\sigma _{{\check \mu }}(A(z))$.
Proof. Since ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$ is rational, both
$\mathbb {L}_{\ell }(\mathfrak {g})$ is rational, both ![]() $A_{(0)}$ and
$A_{(0)}$ and ![]() $\tilde {A}_{(0)}$ acts semisimply on
$\tilde {A}_{(0)}$ acts semisimply on ![]() $C_{\mu }(M{\otimes } N)$ with respect to the twisted action of
$C_{\mu }(M{\otimes } N)$ with respect to the twisted action of ![]() $C(V^{k}(\mathfrak {g}){\otimes } \mathbb {L}_{\ell }(\mathfrak {g}))$ described above, where A is defined in equation (25). Therefore, the assertion follows immediately from Lemma 2.3.
$C(V^{k}(\mathfrak {g}){\otimes } \mathbb {L}_{\ell }(\mathfrak {g}))$ described above, where A is defined in equation (25). Therefore, the assertion follows immediately from Lemma 2.3.
More generally, let
be an element of the extented affine Weyl group ![]() $\tilde {W}=W\ltimes P^{\vee }$, where W is the Weyl group of
$\tilde {W}=W\ltimes P^{\vee }$, where W is the Weyl group of ![]() $\mathfrak {g}$, and let
$\mathfrak {g}$, and let ![]() $\tilde {y}$ be a Tits lifting of y to and automorphism of
$\tilde {y}$ be a Tits lifting of y to and automorphism of ![]() $\mathfrak {g}$ so that
$\mathfrak {g}$ so that ![]() $\tilde {y}(x_{\alpha })=c_{\alpha }x_{y(\alpha )}$ for some
$\tilde {y}(x_{\alpha })=c_{\alpha }x_{y(\alpha )}$ for some ![]() $c_{\alpha }\in \mathbb {C}^{*}$. Then
$c_{\alpha }\in \mathbb {C}^{*}$. Then
defines a Tits lifting of w to an automorphism of ![]() $\widehat {\mathfrak {g}}$. Set
$\widehat {\mathfrak {g}}$. Set
where ![]() $\mathbb {C}_{\hat \chi _{{\check \mu }}}$ is the one-dimensional representation of
$\mathbb {C}_{\hat \chi _{{\check \mu }}}$ is the one-dimensional representation of ![]() $\tilde {w}(\mathfrak {g}_{>0}[t]+\mathfrak {g}_{\geqslant 1}[t,t^{-1}])$ on which
$\tilde {w}(\mathfrak {g}_{>0}[t]+\mathfrak {g}_{\geqslant 1}[t,t^{-1}])$ on which ![]() $\tilde {w}(\mathfrak {g}_{\geqslant 1}[t,t^{-1}])$ acts by the character
$\tilde {w}(\mathfrak {g}_{\geqslant 1}[t,t^{-1}])$ acts by the character ![]() $\hat \chi _{w}: x_{\alpha }t^{n}\mapsto ( x_{\alpha }t^{n}|\tilde {w}(ft^{-1})) $ and
$\hat \chi _{w}: x_{\alpha }t^{n}\mapsto ( x_{\alpha }t^{n}|\tilde {w}(ft^{-1})) $ and ![]() $ \tilde {w}(\mathfrak {g}_{>0}[t])$ acts trivially. Then
$ \tilde {w}(\mathfrak {g}_{>0}[t])$ acts trivially. Then
is equipped with a ![]() $\mathscr {W}^{k}(\mathfrak {g},f)$-module structure.
$\mathscr {W}^{k}(\mathfrak {g},f)$-module structure.
The proof of the following assertion is the same as that of Theorem 7.1.
Theorem 7.2. Let V be a quotient of the universal affine vertex algebra ![]() $V^{k}(\mathfrak {g})$,
$V^{k}(\mathfrak {g})$, ![]() $\ell \in \mathbb {Z}_{\geqslant 0}$, and let
$\ell \in \mathbb {Z}_{\geqslant 0}$, and let ![]() $w\in \tilde {W}$. For any V-module M,
$w\in \tilde {W}$. For any V-module M, ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$-module N, and
$\mathbb {L}_{\ell }(\mathfrak {g})$-module N, and ![]() $i\in \mathbb {Z}$, there is an isomorphism
$i\in \mathbb {Z}$, there is an isomorphism
as modules over ![]() $H_{DS,f}^{0}(V\otimes \mathbb {L}_{\ell }(\mathfrak {g}))\cong H_{DS,f}^{0}(V)\otimes \mathbb {L}_{\ell }(\mathfrak {g})$.
$H_{DS,f}^{0}(V\otimes \mathbb {L}_{\ell }(\mathfrak {g}))\cong H_{DS,f}^{0}(V)\otimes \mathbb {L}_{\ell }(\mathfrak {g})$.
In the above, ![]() $\sigma _{w}^{*} N$ is the twist of N on which
$\sigma _{w}^{*} N$ is the twist of N on which ![]() $A\in \mathbb {L}_{\ell }(\mathfrak {g})$ acts as
$A\in \mathbb {L}_{\ell }(\mathfrak {g})$ acts as ![]() $\sigma _{w}(A(z))$, which is again an integrable representation of
$\sigma _{w}(A(z))$, which is again an integrable representation of ![]() $\widehat {\mathfrak {g}}$ of level
$\widehat {\mathfrak {g}}$ of level ![]() $\ell $.
$\ell $.
Suppose that the grading (11) is even, that is, ![]() $\mathfrak {g}_{j}=0$ unless
$\mathfrak {g}_{j}=0$ unless ![]() $j\in \mathbb {Z}$. Then
$j\in \mathbb {Z}$. Then ![]() $x_{0}\in P^{\vee }$. For a smooth
$x_{0}\in P^{\vee }$. For a smooth ![]() $\widehat {\mathfrak {g}}$-module M of level k, “
$\widehat {\mathfrak {g}}$-module M of level k, “![]() $-$”-Drinfeld–Sokolov reduction
$-$”-Drinfeld–Sokolov reduction ![]() $H_{DS,f,-}^{\bullet }(M)$ ([Reference Frenkel, Kac and WakimotoFKW92, Reference ArakawaAra11]) is nothing but the twisted reduction for
$H_{DS,f,-}^{\bullet }(M)$ ([Reference Frenkel, Kac and WakimotoFKW92, Reference ArakawaAra11]) is nothing but the twisted reduction for ![]() $w=(w_{0},-x_{0})$, where
$w=(w_{0},-x_{0})$, where ![]() $w_{0}$ is the longest element of W:
$w_{0}$ is the longest element of W:
Corollary 7.3. Let V be a quotient of the universal affine vertex algebra ![]() $V^{k}(\mathfrak {g})$,
$V^{k}(\mathfrak {g})$, ![]() $\ell \in \mathbb {Z}_{\geqslant 0}$. Suppose that the grading (11) is even. For any V-module M,
$\ell \in \mathbb {Z}_{\geqslant 0}$. Suppose that the grading (11) is even. For any V-module M, ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$-module N and
$\mathbb {L}_{\ell }(\mathfrak {g})$-module N and ![]() $i\in \mathbb {Z}$, there is an isomorphism
$i\in \mathbb {Z}$, there is an isomorphism
as modules over ![]() $H_{DS,f}^{0}(V\otimes \mathbb {L}_{\ell }(\mathfrak {g}))\cong H_{DS,f}^{0}(V)\otimes \mathbb {L}_{\ell }(\mathfrak {g})$.
$H_{DS,f}^{0}(V\otimes \mathbb {L}_{\ell }(\mathfrak {g}))\cong H_{DS,f}^{0}(V)\otimes \mathbb {L}_{\ell }(\mathfrak {g})$.
8 Higher-rank Urod algebras
In the case that f is a principal nilpotent element ![]() $f_{prin}$, we denote by
$f_{prin}$, we denote by ![]() $\mathscr {W}^{k}(\mathfrak {g})$ the principal W-algebra
$\mathscr {W}^{k}(\mathfrak {g})$ the principal W-algebra ![]() $\mathscr {W}^{k}(\mathfrak {g},f_{prin})$ and by
$\mathscr {W}^{k}(\mathfrak {g},f_{prin})$ and by ![]() $\mathscr {W}_{k}(\mathfrak {g})$ the unique simple quotient of
$\mathscr {W}_{k}(\mathfrak {g})$ the unique simple quotient of ![]() $\mathscr {W}^{k}(\mathfrak {g})$. We have the Feigin–Frenkel duality ([Reference Feigin and FrenkelFF91, Reference Aganagic, Frenkel and OkounkovAFO18]; see also [Reference Arakawa, Creutzig and LinshawACL19]) which states that
$\mathscr {W}^{k}(\mathfrak {g})$. We have the Feigin–Frenkel duality ([Reference Feigin and FrenkelFF91, Reference Aganagic, Frenkel and OkounkovAFO18]; see also [Reference Arakawa, Creutzig and LinshawACL19]) which states that
where ![]() ${}^{L}\mathfrak {g}$ is the Langlands dual Lie algebra and
${}^{L}\mathfrak {g}$ is the Langlands dual Lie algebra and ![]() $\check {k}$ is defined by the formula
$\check {k}$ is defined by the formula ![]() $r^{\vee }(k+h^{\vee })(\check {k}+{}^{L}h^{\vee })=1$. Here,
$r^{\vee }(k+h^{\vee })(\check {k}+{}^{L}h^{\vee })=1$. Here, ![]() $r^{\vee }$ is the lacety of
$r^{\vee }$ is the lacety of ![]() $\mathfrak {g}$, and
$\mathfrak {g}$, and ![]() ${}^{L}h^{\vee }$ is the dual Coxeter number of
${}^{L}h^{\vee }$ is the dual Coxeter number of ![]() ${}^{L}\mathfrak {g}$.
${}^{L}\mathfrak {g}$.
Suppose that ![]() $\mathfrak {g}$ is simply laced and
$\mathfrak {g}$ is simply laced and ![]() $k+h^{\vee }-1\not \in \mathbb {Q}_{\leqslant 0}$. By [Reference Arakawa, Creutzig and LinshawACL19], we have
$k+h^{\vee }-1\not \in \mathbb {Q}_{\leqslant 0}$. By [Reference Arakawa, Creutzig and LinshawACL19], we have
that is, ![]() $\mathscr {W}^{\ell }(\mathfrak {g})$ is isomorphic to the commutant of
$\mathscr {W}^{\ell }(\mathfrak {g})$ is isomorphic to the commutant of ![]() $V^{k}(\mathfrak {g})$ in
$V^{k}(\mathfrak {g})$ in ![]() $V^{k-1}(\mathfrak {g}){\otimes } \mathbb {L}_{1}(\mathfrak {g})$, where
$V^{k-1}(\mathfrak {g}){\otimes } \mathbb {L}_{1}(\mathfrak {g})$, where ![]() $V^{k}(\mathfrak {g})$ is considered as a vertex subalgebra of
$V^{k}(\mathfrak {g})$ is considered as a vertex subalgebra of ![]() $V^{k-1}(\mathfrak {g}){\otimes } \mathbb {L}_{1}(\mathfrak {g})$ by the diagonal embedding and
$V^{k-1}(\mathfrak {g}){\otimes } \mathbb {L}_{1}(\mathfrak {g})$ by the diagonal embedding and ![]() $\ell $ is defined by equation (6). In other words, we have a conformal vertex algebra embedding
$\ell $ is defined by equation (6). In other words, we have a conformal vertex algebra embedding
By Main Theorem 1, (42) induces the conformal vertex algebra homomorphism
which is again embedding by Theorem 3.1. Here, ![]() $\mathcal {U}(\mathfrak {g},f)$ is the vertex algebra
$\mathcal {U}(\mathfrak {g},f)$ is the vertex algebra ![]() $\mathbb {L}_{1}(\mathfrak {g})$ equipped with the Urod conformal vector
$\mathbb {L}_{1}(\mathfrak {g})$ equipped with the Urod conformal vector ![]() $\omega _{Urod}$, which we call the Urod algebra associated with
$\omega _{Urod}$, which we call the Urod algebra associated with ![]() $(\mathfrak {g},f)$. We set
$(\mathfrak {g},f)$. We set
8.1 Generic decompositions
In this subsection, we assume that k is irrational.
For ![]() $(\lambda ,{\check \mu })\in P_{+}\times \check {P}_{+}$, define
$(\lambda ,{\check \mu })\in P_{+}\times \check {P}_{+}$, define
It was shown in [Reference Arakawa and FrenkelAF19] that the ![]() $\mathscr {W}^{k}(\mathfrak {g})$-modules
$\mathscr {W}^{k}(\mathfrak {g})$-modules ![]() $T_{\lambda ,{\check \mu }}^{k}$ are simple, and the isomorphism
$T_{\lambda ,{\check \mu }}^{k}$ are simple, and the isomorphism
holds under the Feigin–Frenkel duality (41).
Let ![]() $\ell $ be nonnegative integer. Then
$\ell $ be nonnegative integer. Then ![]() $\{\mathbb {L}^{\ell }_{\lambda }\mid \lambda \in P^{\ell }_{+}\}$ gives the complete set of isomorphism classes of simple
$\{\mathbb {L}^{\ell }_{\lambda }\mid \lambda \in P^{\ell }_{+}\}$ gives the complete set of isomorphism classes of simple ![]() $\mathbb {L}_{\ell }(\mathfrak {g})$-modules, where
$\mathbb {L}_{\ell }(\mathfrak {g})$-modules, where
is the set of integrable dominant weight of ![]() $\mathfrak {g}$ of level
$\mathfrak {g}$ of level ![]() $\ell $. In particular,
$\ell $. In particular, ![]() $\{\mathbb {L}^{1}_{\lambda }\mid \lambda \in P^{1}_{+}\}$ gives the complete set of isomorphism classes of simple
$\{\mathbb {L}^{1}_{\lambda }\mid \lambda \in P^{1}_{+}\}$ gives the complete set of isomorphism classes of simple ![]() $\mathcal {U}(\mathfrak {g},f)$-modules.
$\mathcal {U}(\mathfrak {g},f)$-modules.
Let
Theorem 8.1. Let ![]() $\mathfrak {g}$ be simply laced, and let f be any nilpotent element of
$\mathfrak {g}$ be simply laced, and let f be any nilpotent element of ![]() $\mathfrak {g}$. For
$\mathfrak {g}$. For ![]() $\lambda ,\mu \in P_{+}$ and
$\lambda ,\mu \in P_{+}$ and ![]() $\nu \in P_{+}^{1}$, we have
$\nu \in P_{+}^{1}$, we have
 $$ \begin{align*} \mathbb{V}^{k-1}_{\mu,f}{\otimes} \mathbb{L}^{1}_{\nu}\cong \bigoplus_{\substack{\lambda\in P_{+}\\ \lambda-\mu-\nu\in Q}}\mathbb{V}^{k}_{\lambda,f}{\otimes} T_{\lambda, \mu}^{\ell} \end{align*} $$
$$ \begin{align*} \mathbb{V}^{k-1}_{\mu,f}{\otimes} \mathbb{L}^{1}_{\nu}\cong \bigoplus_{\substack{\lambda\in P_{+}\\ \lambda-\mu-\nu\in Q}}\mathbb{V}^{k}_{\lambda,f}{\otimes} T_{\lambda, \mu}^{\ell} \end{align*} $$as ![]() $\mathscr {W}^{k}(\mathfrak {g},f){\otimes }\mathscr {W}^{\ell }(\mathfrak {g})$-modules (see equation (43)).
$\mathscr {W}^{k}(\mathfrak {g},f){\otimes }\mathscr {W}^{\ell }(\mathfrak {g})$-modules (see equation (43)).
In the case ![]() $f=f_{prin}$, we have the following more general statement.
$f=f_{prin}$, we have the following more general statement.
Theorem 8.2. Let ![]() $\mathfrak {g}$ is simply laced. For
$\mathfrak {g}$ is simply laced. For ![]() $\lambda ,\mu ,\mu ^{\prime }\in P_{+}$ and
$\lambda ,\mu ,\mu ^{\prime }\in P_{+}$ and ![]() $\nu \in P_{+}^{1}$, we have
$\nu \in P_{+}^{1}$, we have
 $$ \begin{align} T^{k-1}_{\mu,\mu^{\prime}}{\otimes} \mathbb{L}^{1}_{\nu} =\bigoplus_{\substack{\lambda\in P_{+}\\ \lambda-\mu-\mu^{\prime}-\nu\in Q}}T^{k}_{\lambda,\mu^{\prime}}{\otimes} T_{\lambda, \mu}^{\ell} \end{align} $$
$$ \begin{align} T^{k-1}_{\mu,\mu^{\prime}}{\otimes} \mathbb{L}^{1}_{\nu} =\bigoplus_{\substack{\lambda\in P_{+}\\ \lambda-\mu-\mu^{\prime}-\nu\in Q}}T^{k}_{\lambda,\mu^{\prime}}{\otimes} T_{\lambda, \mu}^{\ell} \end{align} $$as ![]() $\mathscr {W}^{k}(\mathfrak {g}){\otimes }\mathscr {W}^{\ell }(\mathfrak {g})$-modules.
$\mathscr {W}^{k}(\mathfrak {g}){\otimes }\mathscr {W}^{\ell }(\mathfrak {g})$-modules.
Note that Theorem 8.2 is compatible with equation (44) since ![]() $\check {(k-1)}=\ell -1$.
$\check {(k-1)}=\ell -1$.
Proof of Theorem 8.1 and Theorem 8.2.
Let ![]() $\lambda ,\mu \in P_{+}$ and
$\lambda ,\mu \in P_{+}$ and ![]() $\nu \in P_{+}^{1}$. By [Reference Arakawa, Creutzig and LinshawACL19, Main Theorem 3], we have
$\nu \in P_{+}^{1}$. By [Reference Arakawa, Creutzig and LinshawACL19, Main Theorem 3], we have
 $$ \begin{align} \mathbb{V}^{k-1}_{\mu}{\otimes} \mathbb{L}^{1}_{\nu}=\bigoplus_{\substack{\lambda\in P_{+}\\ \lambda-\mu-\nu\in Q}} \mathbb{V}^{k}_{\lambda}{\otimes} T^{\ell}_{\lambda,\mu} \end{align} $$
$$ \begin{align} \mathbb{V}^{k-1}_{\mu}{\otimes} \mathbb{L}^{1}_{\nu}=\bigoplus_{\substack{\lambda\in P_{+}\\ \lambda-\mu-\nu\in Q}} \mathbb{V}^{k}_{\lambda}{\otimes} T^{\ell}_{\lambda,\mu} \end{align} $$as ![]() $V^{k+1}(\mathfrak {g}){\otimes }\mathscr {W}^{\ell }(\mathfrak {g})$-modules. Applying Main Theorem 1 to
$V^{k+1}(\mathfrak {g}){\otimes }\mathscr {W}^{\ell }(\mathfrak {g})$-modules. Applying Main Theorem 1 to ![]() $\mathbb {V}^{k-1}_{\mu }{\otimes } \mathbb {L}^{1}_{\nu }$, we obtain Theorem 8.1. Next, under the identification
$\mathbb {V}^{k-1}_{\mu }{\otimes } \mathbb {L}^{1}_{\nu }$, we obtain Theorem 8.1. Next, under the identification ![]() $P/Q\cong P^{1}_{+}$, we have
$P/Q\cong P^{1}_{+}$, we have ![]() $\sigma _{\mu ^{\prime }}^{*}\mathbb {L}^{1}_{\nu +\mu ^{\prime }+Q}\cong \mathbb {L}^{1}_{\nu +Q}$. Hence, we obtain Theorem 8.2 by applying Theorem 7.1.
$\sigma _{\mu ^{\prime }}^{*}\mathbb {L}^{1}_{\nu +\mu ^{\prime }+Q}\cong \mathbb {L}^{1}_{\nu +Q}$. Hence, we obtain Theorem 8.2 by applying Theorem 7.1.
Let ![]() $\pi ^{k}$ be the Heisenberg vertex subalgebra of
$\pi ^{k}$ be the Heisenberg vertex subalgebra of ![]() $V^{k}(\mathfrak {g})$ generated by
$V^{k}(\mathfrak {g})$ generated by ![]() $h(z)$,
$h(z)$, ![]() $h\in \mathfrak {h}$, and let
$h\in \mathfrak {h}$, and let ![]() $\pi ^{k}_{\lambda }$ be the irreducible highest weight representation of
$\pi ^{k}_{\lambda }$ be the irreducible highest weight representation of ![]() $\pi ^{k}$ with highest weight
$\pi ^{k}$ with highest weight ![]() $\lambda $. There is a vertex algebra embedding
$\lambda $. There is a vertex algebra embedding
called the Miura map ([Reference Feĭgin and FrenkelFF90b]; see also [Reference ArakawaAra17]), and hence, each ![]() $\pi ^{k+h^{\vee }}_{\lambda }$ is a
$\pi ^{k+h^{\vee }}_{\lambda }$ is a ![]() $\mathscr {W}^{k}(\mathfrak {g})$-module.
$\mathscr {W}^{k}(\mathfrak {g})$-module.
Theorem 8.3. Let ![]() $\mathfrak {g}$ is simply laced,
$\mathfrak {g}$ is simply laced, ![]() $\mu \in \mathfrak {h}^{*}$ be generic,
$\mu \in \mathfrak {h}^{*}$ be generic, ![]() $\nu \in P^{1}_{+}$. We have the isomorphism
$\nu \in P^{1}_{+}$. We have the isomorphism
 $$ \begin{align*} \pi_{\mu}^{k-1+h^{\vee}}{\otimes} \mathbb{L}^{1}_{\nu}\cong \bigoplus_{\lambda \in \mathfrak{h}^{*} \atop \lambda-\mu-\nu\in Q} \pi^{k+h^{\vee}}_{\lambda}{\otimes} \pi^{\ell+h^{\vee}}_{\lambda-(\ell+h^{\vee})\mu} \end{align*} $$
$$ \begin{align*} \pi_{\mu}^{k-1+h^{\vee}}{\otimes} \mathbb{L}^{1}_{\nu}\cong \bigoplus_{\lambda \in \mathfrak{h}^{*} \atop \lambda-\mu-\nu\in Q} \pi^{k+h^{\vee}}_{\lambda}{\otimes} \pi^{\ell+h^{\vee}}_{\lambda-(\ell+h^{\vee})\mu} \end{align*} $$as ![]() $\mathscr {W}^{k}(\mathfrak {g}){\otimes } \mathscr {W}^{\ell }(\mathfrak {g})$-modules.
$\mathscr {W}^{k}(\mathfrak {g}){\otimes } \mathscr {W}^{\ell }(\mathfrak {g})$-modules.
For a generic ![]() $\lambda \in \mathfrak {h}^{*}$, the
$\lambda \in \mathfrak {h}^{*}$, the ![]() $\mathscr {W}^{k}(\mathfrak {g})$-module
$\mathscr {W}^{k}(\mathfrak {g})$-module ![]() $\pi ^{k+h^{\vee }}_{\lambda }$ is irreducible and isomorphic to a Verma module
$\pi ^{k+h^{\vee }}_{\lambda }$ is irreducible and isomorphic to a Verma module ![]() $\mathbb {M}^{k}(\chi _{\lambda })$ with highest weight ([Reference Feigin and FrenkelFF90a, Reference FrenkelFre92, Reference ArakawaAra07]). Here,
$\mathbb {M}^{k}(\chi _{\lambda })$ with highest weight ([Reference Feigin and FrenkelFF90a, Reference FrenkelFre92, Reference ArakawaAra07]). Here, ![]() $\chi _{\lambda }:\operatorname {Zhu}(\mathscr {W}^{k}(\mathfrak {g}))\rightarrow \mathbb {C}$ is described in [Reference Arakawa, Creutzig and LinshawACL19, (27)], where
$\chi _{\lambda }:\operatorname {Zhu}(\mathscr {W}^{k}(\mathfrak {g}))\rightarrow \mathbb {C}$ is described in [Reference Arakawa, Creutzig and LinshawACL19, (27)], where ![]() $\operatorname {Zhu}(\mathscr {W}^{k}(\mathfrak {g}))$ is the Zhu algebra of
$\operatorname {Zhu}(\mathscr {W}^{k}(\mathfrak {g}))$ is the Zhu algebra of ![]() $\mathscr {W}^{k}(\mathfrak {g})$. Hence, the following assertion immediately follows from Theorem 8.3.
$\mathscr {W}^{k}(\mathfrak {g})$. Hence, the following assertion immediately follows from Theorem 8.3.
Corollary 8.4. Let ![]() $\mathfrak {g}$ is simply laced,
$\mathfrak {g}$ is simply laced, ![]() $\mu \in \mathfrak {h}^{*}$ be generic,
$\mu \in \mathfrak {h}^{*}$ be generic, ![]() $\nu \in P^{1}_{+}$. We have the isomorphism
$\nu \in P^{1}_{+}$. We have the isomorphism
 $$ \begin{align*} \mathbb{M}^{k-1}(\chi_{\mu}){\otimes} \mathbb{L}^{1}_{\nu}\cong \bigoplus_{\lambda \in \mathfrak{h}^{*} \atop \lambda-\mu-\nu\in Q} \mathbb{M}^{k}(\chi_{\lambda}){\otimes}\mathbb{M}^{\ell}(\chi_{\lambda-(\ell+h^{\vee})\mu}) \end{align*} $$
$$ \begin{align*} \mathbb{M}^{k-1}(\chi_{\mu}){\otimes} \mathbb{L}^{1}_{\nu}\cong \bigoplus_{\lambda \in \mathfrak{h}^{*} \atop \lambda-\mu-\nu\in Q} \mathbb{M}^{k}(\chi_{\lambda}){\otimes}\mathbb{M}^{\ell}(\chi_{\lambda-(\ell+h^{\vee})\mu}) \end{align*} $$as ![]() $\mathscr {W}^{k}(\mathfrak {g}){\otimes } \mathscr {W}^{\ell }(\mathfrak {g})$-modules.
$\mathscr {W}^{k}(\mathfrak {g}){\otimes } \mathscr {W}^{\ell }(\mathfrak {g})$-modules.
Let ![]() $\mathbb {W}^{k}_{{\lambda }}$ be the Wakimoto module [Reference Feĭgin and FrenkelFF90b] of
$\mathbb {W}^{k}_{{\lambda }}$ be the Wakimoto module [Reference Feĭgin and FrenkelFF90b] of ![]() $\widehat {\mathfrak {g}}$ at level k with highest weight
$\widehat {\mathfrak {g}}$ at level k with highest weight ![]() $\lambda \in \mathfrak {h}^{*}$. For
$\lambda \in \mathfrak {h}^{*}$. For ![]() $\lambda =0$,
$\lambda =0$, ![]() $\mathbb {W}^{k}:=\mathbb {W}^{k}_{0}$ is a vertex algebra, and we have an embedding
$\mathbb {W}^{k}:=\mathbb {W}^{k}_{0}$ is a vertex algebra, and we have an embedding ![]() $V^{k}(\mathfrak {g})\hookrightarrow \mathbb {W}^{k}$ of vertex algebras ([Reference Feĭgin and FrenkelFF90b, Reference FrenkelFre05]). We have
$V^{k}(\mathfrak {g})\hookrightarrow \mathbb {W}^{k}$ of vertex algebras ([Reference Feĭgin and FrenkelFF90b, Reference FrenkelFre05]). We have ![]() $H_{DS,f_{prin}}^{i}( \mathbb {W}^{k}_{\lambda })\cong \delta _{i,0}\pi ^{k+h^{\vee }}_{\lambda }$, and the Miura map is by definition [Reference Feĭgin and FrenkelFF90b] the map
$H_{DS,f_{prin}}^{i}( \mathbb {W}^{k}_{\lambda })\cong \delta _{i,0}\pi ^{k+h^{\vee }}_{\lambda }$, and the Miura map is by definition [Reference Feĭgin and FrenkelFF90b] the map ![]() $\mathscr {W}^{k}(\mathfrak {g})\rightarrow H_{DS,f_{prin}}^{0}( \mathbb {W}^{k})\cong \pi ^{k+h^{\vee }}$ induced by the embedding
$\mathscr {W}^{k}(\mathfrak {g})\rightarrow H_{DS,f_{prin}}^{0}( \mathbb {W}^{k})\cong \pi ^{k+h^{\vee }}$ induced by the embedding ![]() $V^{k}(\mathfrak {g})\hookrightarrow \mathbb {W}^{k}$.
$V^{k}(\mathfrak {g})\hookrightarrow \mathbb {W}^{k}$.
Proof of Theorem 8.3.
Since ![]() $\nu $ is generic,
$\nu $ is generic, ![]() $\mathbb {W}^{k-1}_{\mu }{\otimes } \mathbb {L}^{1}_{\nu }$ is a direct sum of irreducible Verma modules as a diagonal
$\mathbb {W}^{k-1}_{\mu }{\otimes } \mathbb {L}^{1}_{\nu }$ is a direct sum of irreducible Verma modules as a diagonal ![]() $\widehat {\mathfrak {g}}$-module or, equivalently, a direct sum of irreducible Wakimoto modules
$\widehat {\mathfrak {g}}$-module or, equivalently, a direct sum of irreducible Wakimoto modules ![]() $\mathbb {W}^{k}_{\lambda }$. So we can write
$\mathbb {W}^{k}_{\lambda }$. So we can write ![]() $\mathbb {W}^{k-1}_{\mu }{\otimes } \mathbb {L}^{1}_{\nu }=\bigoplus _{\lambda \in \mathfrak {h}^{*}}\mathbb {W}^{k}_{\lambda {\otimes }} m_{\mu ,\nu }^{\lambda }$, where
$\mathbb {W}^{k-1}_{\mu }{\otimes } \mathbb {L}^{1}_{\nu }=\bigoplus _{\lambda \in \mathfrak {h}^{*}}\mathbb {W}^{k}_{\lambda {\otimes }} m_{\mu ,\nu }^{\lambda }$, where ![]() $m_{\mu ,\nu }^{\lambda }$ be the multiplicity of
$m_{\mu ,\nu }^{\lambda }$ be the multiplicity of ![]() $\mathbb {W}^{k}_{\lambda }$ in
$\mathbb {W}^{k}_{\lambda }$ in ![]() $\mathbb {W}^{k-1}_{\mu }{\otimes } \mathbb {L}^{1}_{\nu }$. Note that
$\mathbb {W}^{k-1}_{\mu }{\otimes } \mathbb {L}^{1}_{\nu }$. Note that ![]() $m_{\mu ,\nu }^{\lambda }$ is a
$m_{\mu ,\nu }^{\lambda }$ is a ![]() $\mathscr {W}^{\ell }(\mathfrak {g})$-module by equation (42). We have
$\mathscr {W}^{\ell }(\mathfrak {g})$-module by equation (42). We have
 $$ \begin{align*} m_{\mu,\nu}^{\lambda}\cong \operatorname{\mathrm{Hom}}_{\pi^{k+1+h^{\vee}}}(\pi^{k+1+h^{\vee}}_{\lambda}, H^{\infty/2+0}({\mathfrak n}[t,t^{-1}],\mathbb{W}^{k-1}_{\mu}{\otimes} \mathbb{L}^{1}_{\nu})\\ \cong \begin{cases} \pi^{\ell+h^{\vee}}_{\mu-(\ell+h^{\vee})\lambda}&\text{if }\lambda-\mu-\nu\in Q,\\ 0&\text{otherwise } \end{cases} \end{align*} $$
$$ \begin{align*} m_{\mu,\nu}^{\lambda}\cong \operatorname{\mathrm{Hom}}_{\pi^{k+1+h^{\vee}}}(\pi^{k+1+h^{\vee}}_{\lambda}, H^{\infty/2+0}({\mathfrak n}[t,t^{-1}],\mathbb{W}^{k-1}_{\mu}{\otimes} \mathbb{L}^{1}_{\nu})\\ \cong \begin{cases} \pi^{\ell+h^{\vee}}_{\mu-(\ell+h^{\vee})\lambda}&\text{if }\lambda-\mu-\nu\in Q,\\ 0&\text{otherwise } \end{cases} \end{align*} $$as ![]() $\mathscr {W}^{\ell }(\mathfrak {g})$-modules by [Reference Arakawa, Creutzig and LinshawACL19, Proposition 8.3]. The assertion follows by applying Main Theorem 1 to
$\mathscr {W}^{\ell }(\mathfrak {g})$-modules by [Reference Arakawa, Creutzig and LinshawACL19, Proposition 8.3]. The assertion follows by applying Main Theorem 1 to
 $$ \begin{align} \mathbb{W}^{k-1}_{\mu}{\otimes} \mathbb{L}^{1}_{\nu}=\bigoplus\limits_{\lambda\in \mathfrak{h}^{*} \atop \lambda-\mu-\nu\in Q}\mathbb{W}^{k}_{\lambda{\otimes}} \pi_{\mu-(\ell+h^{\vee})}. \end{align} $$
$$ \begin{align} \mathbb{W}^{k-1}_{\mu}{\otimes} \mathbb{L}^{1}_{\nu}=\bigoplus\limits_{\lambda\in \mathfrak{h}^{*} \atop \lambda-\mu-\nu\in Q}\mathbb{W}^{k}_{\lambda{\otimes}} \pi_{\mu-(\ell+h^{\vee})}. \end{align} $$8.2 Decomposition at admissible levels
Let k be an admissible number for ![]() $\widehat {\mathfrak {g}}$, that is,
$\widehat {\mathfrak {g}}$, that is, ![]() $\mathbb {L}_{k}(\mathfrak {g})$ is admissible ([Reference Kac and WakimotoKW89]) as a
$\mathbb {L}_{k}(\mathfrak {g})$ is admissible ([Reference Kac and WakimotoKW89]) as a ![]() $\widehat {\mathfrak {g}}$-module. In the case that
$\widehat {\mathfrak {g}}$-module. In the case that ![]() $\mathfrak {g}$ is simply laced, this condition is equivalent to
$\mathfrak {g}$ is simply laced, this condition is equivalent to
For an admissible number k, a simple module over ![]() $\mathbb {L}_{k}(\mathfrak {g})$ need not be ordinary, that is, in
$\mathbb {L}_{k}(\mathfrak {g})$ need not be ordinary, that is, in ![]() $\operatorname {KL}$, unless k is a nonnegative integer. The classification of simple highest weight representations of
$\operatorname {KL}$, unless k is a nonnegative integer. The classification of simple highest weight representations of ![]() $\mathbb {L}_{k}(\mathfrak {g})$ was given in [Reference ArakawaAra16a]. For our purpose, we need only the ordinary representations of
$\mathbb {L}_{k}(\mathfrak {g})$ was given in [Reference ArakawaAra16a]. For our purpose, we need only the ordinary representations of ![]() $\mathbb {L}_{k}(\mathfrak {g})$. By [Reference ArakawaAra16a], the complete set of isomorphism classes of ordinary simple
$\mathbb {L}_{k}(\mathfrak {g})$. By [Reference ArakawaAra16a], the complete set of isomorphism classes of ordinary simple ![]() $\mathbb {L}_{k}(\mathfrak {g})$-modules is given by
$\mathbb {L}_{k}(\mathfrak {g})$-modules is given by
where ![]() $Adm_{\mathbb {Z}}^{k}=\{\lambda \in P_{+}\mid \mathbb {L}^{k}_{\lambda }\text { is admissible}\}$. We have
$Adm_{\mathbb {Z}}^{k}=\{\lambda \in P_{+}\mid \mathbb {L}^{k}_{\lambda }\text { is admissible}\}$. We have
if ![]() $\mathfrak {g}$ is simply laced and k is of the form (49).
$\mathfrak {g}$ is simply laced and k is of the form (49).
Let k be an admissible number and ![]() $\lambda \in Adm^{k}_{\mathbb {Z}}$. By [Reference ArakawaAra15a], the associated variety
$\lambda \in Adm^{k}_{\mathbb {Z}}$. By [Reference ArakawaAra15a], the associated variety ![]() $X_{\mathbb {L}^{k}_{\lambda }}$ [Reference ArakawaAra12] of
$X_{\mathbb {L}^{k}_{\lambda }}$ [Reference ArakawaAra12] of ![]() $\mathbb {L}^{k}_{\lambda }$ is the closure of some nilpotent orbit
$\mathbb {L}^{k}_{\lambda }$ is the closure of some nilpotent orbit ![]() $\mathbb {O}_{k}$ which depends only on the denominator q of k. More explicitly, we have
$\mathbb {O}_{k}$ which depends only on the denominator q of k. More explicitly, we have
in the case that ![]() $\mathfrak {g}$ is simply laced. By [Reference ArakawaAra15a], we have
$\mathfrak {g}$ is simply laced. By [Reference ArakawaAra15a], we have
An admissible number k is called nondegenerate if ![]() $ X_{\mathbb {L}^{k}_{\lambda }}$ equals to the nilpotent cone
$ X_{\mathbb {L}^{k}_{\lambda }}$ equals to the nilpotent cone ![]() $\mathcal {N}$ of
$\mathcal {N}$ of ![]() $\mathfrak {g}$ for some
$\mathfrak {g}$ for some ![]() $\lambda \in Adm^{k}_{\mathbb {Z}}$ or, equivalently, for all
$\lambda \in Adm^{k}_{\mathbb {Z}}$ or, equivalently, for all ![]() $Adm^{k}_{\mathbb {Z}}$. In the case that
$Adm^{k}_{\mathbb {Z}}$. In the case that ![]() $\mathfrak {g}$ is simply laced, this happens if and only if the denominator q of k is equal or greater than
$\mathfrak {g}$ is simply laced, this happens if and only if the denominator q of k is equal or greater than ![]() $h^{\vee }$. If this is the case, the simple principal W-algebra
$h^{\vee }$. If this is the case, the simple principal W-algebra ![]() $\mathscr {W}_{k}(\mathfrak {g})=\mathscr {W}_{k}(\mathfrak {g},f_{prin})$ is rational and lisse ([Reference ArakawaAra15a, Reference ArakawaAra15b]), and the complete set of the isomorphism classes of
$\mathscr {W}_{k}(\mathfrak {g})=\mathscr {W}_{k}(\mathfrak {g},f_{prin})$ is rational and lisse ([Reference ArakawaAra15a, Reference ArakawaAra15b]), and the complete set of the isomorphism classes of ![]() $\mathscr {W}_{k}(\mathfrak {g})$-module is given by
$\mathscr {W}_{k}(\mathfrak {g})$-module is given by
where
and ![]() $\tilde {W}_{+}$ is the subgroup of the extended affine Weyl group of
$\tilde {W}_{+}$ is the subgroup of the extended affine Weyl group of ![]() $\mathfrak {g}$ consisting of elements of length zero that acts on the set
$\mathfrak {g}$ consisting of elements of length zero that acts on the set ![]() $Adm_{\mathbb {Z}}^{k}\times Adm_{\mathbb {Z}}^{\check {k}}$ diagonally. We have
$Adm_{\mathbb {Z}}^{k}\times Adm_{\mathbb {Z}}^{\check {k}}$ diagonally. We have
under the Feigin–Frenkel duality.
The following assertion is new for nonzero ![]() ${\check \mu }$.
${\check \mu }$.
Theorem 8.5. Let k be a nondegenerate admissible number, and let ![]() $\lambda \in Adm_{\mathbb {Z}}^{k}$,
$\lambda \in Adm_{\mathbb {Z}}^{k}$, ![]() ${\check \mu }\in Adm_{\mathbb {Z}}^{\check {k}}$. We have
${\check \mu }\in Adm_{\mathbb {Z}}^{\check {k}}$. We have
 $$ \begin{align*}H_{DS,f_{prin},{\check\mu}}^{i}(\mathbb{L}^{k}_{\lambda})\cong \begin{cases} \mathbf{L}^{k}_{[\lambda,{\check\mu}]}&\text{for }i=0,\\ 0&\text{for }i\ne 0 \end{cases}\end{align*} $$
$$ \begin{align*}H_{DS,f_{prin},{\check\mu}}^{i}(\mathbb{L}^{k}_{\lambda})\cong \begin{cases} \mathbf{L}^{k}_{[\lambda,{\check\mu}]}&\text{for }i=0,\\ 0&\text{for }i\ne 0 \end{cases}\end{align*} $$as ![]() $\mathscr {W}^{k}(\mathfrak {g})$-modules.
$\mathscr {W}^{k}(\mathfrak {g})$-modules.
Proof. The case ![]() ${\check \mu }=0$ has been proved in [Reference ArakawaAra04, Reference ArakawaAra07]. In particular,
${\check \mu }=0$ has been proved in [Reference ArakawaAra04, Reference ArakawaAra07]. In particular,
By [Reference Arakawa and FrenkelAF19, Theorem 2.1], we have ![]() $H_{DS,f_{prin},{\check \mu }}^{i}(\mathbb {V}^{k}_{\lambda })=0$ for all
$H_{DS,f_{prin},{\check \mu }}^{i}(\mathbb {V}^{k}_{\lambda })=0$ for all ![]() $i\ne 0$,
$i\ne 0$, ![]() $\lambda \in P_{+}$. It follows that
$\lambda \in P_{+}$. It follows that ![]() $H_{DS,f_{prin},{\check \mu }}^{i\ne 0}(M)=0$,
$H_{DS,f_{prin},{\check \mu }}^{i\ne 0}(M)=0$, ![]() $i\ne 0$, for any object M in
$i\ne 0$, for any object M in ![]() $\operatorname {KL}$ that admits a Weyl flag. This implies that
$\operatorname {KL}$ that admits a Weyl flag. This implies that
see the proof of [Reference ArakawaAra04, Theorem 8.3].
By [Reference ArakawaAra14], the admissible representation ![]() $\mathbb {L}^{k}_{\lambda }$ admits a two-sided resolution
$\mathbb {L}^{k}_{\lambda }$ admits a two-sided resolution
of the form  $C^{i}=\bigoplus \limits _{w\in \widehat {W}(\lambda +k\Lambda _{0})\atop \ell ^{\infty /2}(w)=i}\mathbb {W}^{k}_{w\circ {\lambda }}$, where
$C^{i}=\bigoplus \limits _{w\in \widehat {W}(\lambda +k\Lambda _{0})\atop \ell ^{\infty /2}(w)=i}\mathbb {W}^{k}_{w\circ {\lambda }}$, where ![]() $\widehat {W}(\lambda +k\Lambda _{0})$ is the integral Weyl group of
$\widehat {W}(\lambda +k\Lambda _{0})$ is the integral Weyl group of ![]() $\lambda +k\Lambda _{0}$ and
$\lambda +k\Lambda _{0}$ and ![]() $\ell ^{\infty /2}(w)$ is the semi-infinite length of w. By [Reference Arakawa and FrenkelAF19, Lemma 3.2], we have
$\ell ^{\infty /2}(w)$ is the semi-infinite length of w. By [Reference Arakawa and FrenkelAF19, Lemma 3.2], we have
 $$ \begin{align*}H_{DS,f_{prin},{\check\mu}}^{0}(\mathbb{W}^{k}_{{\lambda}})\cong \begin{cases} \pi_{\lambda-(k+h^{\vee}){\check\mu}}^{k}&\text{for }i=0,\\ 0&\text{for }i\ne 0 \end{cases}\end{align*} $$
$$ \begin{align*}H_{DS,f_{prin},{\check\mu}}^{0}(\mathbb{W}^{k}_{{\lambda}})\cong \begin{cases} \pi_{\lambda-(k+h^{\vee}){\check\mu}}^{k}&\text{for }i=0,\\ 0&\text{for }i\ne 0 \end{cases}\end{align*} $$as ![]() $\mathscr {W}^{k}(\mathfrak {g})$-modules. It follows that
$\mathscr {W}^{k}(\mathfrak {g})$-modules. It follows that ![]() $H_{DS,f_{prin},{\check \mu }}^{i}(\mathbb {L}^{k}_{\lambda })$ is the i-th cohomology of the complex obtained by applying the functor
$H_{DS,f_{prin},{\check \mu }}^{i}(\mathbb {L}^{k}_{\lambda })$ is the i-th cohomology of the complex obtained by applying the functor ![]() $H_{DS,f_{prin},{\check \mu }}^{0}(?)$ to the resolution (58). In particular,
$H_{DS,f_{prin},{\check \mu }}^{0}(?)$ to the resolution (58). In particular, ![]() $H_{DS,f_{prin},{\check \mu }}^{i}(\mathbb {L}^{k}_{\lambda })$ is a subquotient of the
$H_{DS,f_{prin},{\check \mu }}^{i}(\mathbb {L}^{k}_{\lambda })$ is a subquotient of the ![]() $\mathscr {W}^{k}(\mathfrak {g})$-module
$\mathscr {W}^{k}(\mathfrak {g})$-module
 $$ \begin{align*}H_{DS,f_{prin},{\check\mu}}^{0}(C^{i})\cong \bigoplus\limits_{w\in \widehat{W}(\lambda+k\Lambda_{0})\atop \ell^{\infty/2}(w)=i}\pi^{k}_{w\circ \lambda-(k+h^{\vee}){\check\mu}}.\end{align*} $$
$$ \begin{align*}H_{DS,f_{prin},{\check\mu}}^{0}(C^{i})\cong \bigoplus\limits_{w\in \widehat{W}(\lambda+k\Lambda_{0})\atop \ell^{\infty/2}(w)=i}\pi^{k}_{w\circ \lambda-(k+h^{\vee}){\check\mu}}.\end{align*} $$On the other hand, since ![]() $\mathbb {L}^{k}_{\lambda }$ is a
$\mathbb {L}^{k}_{\lambda }$ is a ![]() $\mathbb {L}_{k}(\mathfrak {g})$-module, each
$\mathbb {L}_{k}(\mathfrak {g})$-module, each ![]() $H_{DS,f_{prin},{\check \mu }}^{i}(\mathbb {L}^{k}_{\lambda })$ is a module over the simple W-algebra
$H_{DS,f_{prin},{\check \mu }}^{i}(\mathbb {L}^{k}_{\lambda })$ is a module over the simple W-algebra ![]() $\mathscr {W}_{k}(\mathfrak {g})=H_{DS,f_{prin}}^{0}(\mathbb {L}_{k}(\mathfrak {g}))$. Since
$\mathscr {W}_{k}(\mathfrak {g})=H_{DS,f_{prin}}^{0}(\mathbb {L}_{k}(\mathfrak {g}))$. Since ![]() $\mathscr {W}_{k}(\mathfrak {g})$ is rational,
$\mathscr {W}_{k}(\mathfrak {g})$ is rational, ![]() $H_{DS,f_{prin},{\check \mu }}^{i}(\mathbb {L}^{k}_{\lambda })$ is a direct sum of simple modules of the form (53). However, such a module appears in the local composition factor of
$H_{DS,f_{prin},{\check \mu }}^{i}(\mathbb {L}^{k}_{\lambda })$ is a direct sum of simple modules of the form (53). However, such a module appears in the local composition factor of ![]() $\pi ^{k}_{w\circ \lambda -(k+h^{\vee }){\check \mu }}$ if and only if
$\pi ^{k}_{w\circ \lambda -(k+h^{\vee }){\check \mu }}$ if and only if ![]() $w\in W$ ([Reference ArakawaAra07]), where
$w\in W$ ([Reference ArakawaAra07]), where ![]() $W\subset \widehat {W}(k\Lambda _{0})$ is the Weyl group of
$W\subset \widehat {W}(k\Lambda _{0})$ is the Weyl group of ![]() $\mathfrak {g}$. As
$\mathfrak {g}$. As
![]() $H_{DS,f_{prin},{\check \mu }}^{i}(\mathbb {L}^{k}_{\lambda })$ must vanish for
$H_{DS,f_{prin},{\check \mu }}^{i}(\mathbb {L}^{k}_{\lambda })$ must vanish for ![]() $i< 0$. Together with equation (57), we get
$i< 0$. Together with equation (57), we get ![]() $H_{DS,f_{prin},{\check \mu }}^{i}(\mathbb {L}^{k}_{\lambda })=0$ for
$H_{DS,f_{prin},{\check \mu }}^{i}(\mathbb {L}^{k}_{\lambda })=0$ for ![]() $i\ne 0$. Finally, since
$i\ne 0$. Finally, since ![]() $\mathbf {L}^{k}_{[\lambda ,{\check \mu }]}$ is the unique simple
$\mathbf {L}^{k}_{[\lambda ,{\check \mu }]}$ is the unique simple ![]() $\mathscr {W}_{k}(\mathfrak {g})$-module that appears in the local composition factor of
$\mathscr {W}_{k}(\mathfrak {g})$-module that appears in the local composition factor of ![]() $\pi ^{k}_{\lambda -(k+h^{\vee }){\check \mu }}$ and it appears with multiplicity one ([Reference ArakawaAra07]),
$\pi ^{k}_{\lambda -(k+h^{\vee }){\check \mu }}$ and it appears with multiplicity one ([Reference ArakawaAra07]), ![]() $H_{DS,f_{prin},{\check \mu }}^{i}(\mathbb {L}^{k}_{\lambda })$ is either zero or isomorphic to
$H_{DS,f_{prin},{\check \mu }}^{i}(\mathbb {L}^{k}_{\lambda })$ is either zero or isomorphic to ![]() $\mathbf {L}^{k}_{[\lambda ,{\check \mu }]}$. The assertion follows since the Euler character of
$\mathbf {L}^{k}_{[\lambda ,{\check \mu }]}$. The assertion follows since the Euler character of ![]() $H_{DS,f_{prin}}^{\bullet }(\mathbb {L}_{k}(\mathfrak {g}))$ is equal to the character of
$H_{DS,f_{prin}}^{\bullet }(\mathbb {L}_{k}(\mathfrak {g}))$ is equal to the character of ![]() $\mathbf {L}^{k}_{[\lambda ,{\check \mu }]}$.
$\mathbf {L}^{k}_{[\lambda ,{\check \mu }]}$.
For an admissible number k and ![]() $\lambda \in Adm^{k}_{\mathbb {Z}}$, define
$\lambda \in Adm^{k}_{\mathbb {Z}}$, define
Note that ![]() $\mathbb {L}^{k}_{\lambda ,f_{prin}}=\mathbf {L}_{[\lambda ,0]}^{k}\cong \mathbf {L}_{[0,\lambda ]}^{\check {k}}$.
$\mathbb {L}^{k}_{\lambda ,f_{prin}}=\mathbf {L}_{[\lambda ,0]}^{k}\cong \mathbf {L}_{[0,\lambda ]}^{\check {k}}$.
Let ![]() $\mathfrak {g}$ be simply laced. Observe that if
$\mathfrak {g}$ be simply laced. Observe that if ![]() $k-1$ is an admissible number, then so is k, and
$k-1$ is an admissible number, then so is k, and ![]() $\ell $ is a nondegenerate admissible number. Moreover, we have
$\ell $ is a nondegenerate admissible number. Moreover, we have
if ![]() $k-h^{\vee }+1=p/q$ with
$k-h^{\vee }+1=p/q$ with ![]() $p\geqslant h^{\vee }$,
$p\geqslant h^{\vee }$, ![]() $q\geqslant 1$,
$q\geqslant 1$, ![]() $(p,q)=1$.
$(p,q)=1$.
Theorem 8.6. Let ![]() $\mathfrak {g}$ be simply laced, and let
$\mathfrak {g}$ be simply laced, and let ![]() $k-1 $ be admissible. Suppose that
$k-1 $ be admissible. Suppose that ![]() $f\in X_{\mathbb {L}_{k}(\mathfrak {g})}=X_{\mathbb {L}_{k-1}(\mathfrak {g})}$. For
$f\in X_{\mathbb {L}_{k}(\mathfrak {g})}=X_{\mathbb {L}_{k-1}(\mathfrak {g})}$. For ![]() $\mu \in Adm^{k-1}_{\mathbb {Z}}$,
$\mu \in Adm^{k-1}_{\mathbb {Z}}$, ![]() $\nu \in P_{+}^{1}$, we have
$\nu \in P_{+}^{1}$, we have
 $$ \begin{align*} \mathbb{L}^{k-1}_{\mu,f}\otimes \mathbb{L}^{1}_{\nu}\cong \bigoplus_{\lambda\in Adm^{k}_{\mathbb{Z}}\atop \lambda-\mu-\nu\in Q} \mathbb{L}^{k}_{\lambda,f}\otimes \mathbf{L}_{[\lambda,\mu]}^{\ell} \end{align*} $$
$$ \begin{align*} \mathbb{L}^{k-1}_{\mu,f}\otimes \mathbb{L}^{1}_{\nu}\cong \bigoplus_{\lambda\in Adm^{k}_{\mathbb{Z}}\atop \lambda-\mu-\nu\in Q} \mathbb{L}^{k}_{\lambda,f}\otimes \mathbf{L}_{[\lambda,\mu]}^{\ell} \end{align*} $$as ![]() $\mathscr {W}^{k}(\mathfrak {g},f){\otimes } \mathscr {W}^{\ell }(\mathfrak {g})$-modules.
$\mathscr {W}^{k}(\mathfrak {g},f){\otimes } \mathscr {W}^{\ell }(\mathfrak {g})$-modules.
In the case ![]() $f=f_{prin}$, we have the following more general statement.
$f=f_{prin}$, we have the following more general statement.
Theorem 8.7. Let ![]() $\mathfrak {g}$ be simply laced, and let
$\mathfrak {g}$ be simply laced, and let ![]() $k-1 $ be nondegenerate admissible. For
$k-1 $ be nondegenerate admissible. For ![]() $\mu \in Adm^{k-1}_{\mathbb {Z}}$,
$\mu \in Adm^{k-1}_{\mathbb {Z}}$, ![]() $\mu ^{\prime }\in Adm^{\check {k-1}}_{\mathbb {Z}}=Adm^{\check {k}}_{\mathbb {Z}}$,
$\mu ^{\prime }\in Adm^{\check {k-1}}_{\mathbb {Z}}=Adm^{\check {k}}_{\mathbb {Z}}$, ![]() $\nu \in P_{+}^{1}$, we have
$\nu \in P_{+}^{1}$, we have
 $$ \begin{align*} \mathbf{L}_{[\mu,\mu^{\prime}]}^{k-1}\otimes \mathbb{L}^{1}_{\nu}\cong \bigoplus_{\lambda\in Adm^{k}_{\mathbb{Z}}\atop \lambda-\mu-\mu^{\prime}-\nu\in Q} \mathbf{L}_{[\lambda,\mu^{\prime}]}^{k}\otimes \mathbf{L}_{[\lambda,\mu]}^{\ell} \end{align*} $$
$$ \begin{align*} \mathbf{L}_{[\mu,\mu^{\prime}]}^{k-1}\otimes \mathbb{L}^{1}_{\nu}\cong \bigoplus_{\lambda\in Adm^{k}_{\mathbb{Z}}\atop \lambda-\mu-\mu^{\prime}-\nu\in Q} \mathbf{L}_{[\lambda,\mu^{\prime}]}^{k}\otimes \mathbf{L}_{[\lambda,\mu]}^{\ell} \end{align*} $$as ![]() $\mathscr {W}_{k}(\mathfrak {g}){\otimes } \mathscr {W}_{\ell }(\mathfrak {g})$-modules.
$\mathscr {W}_{k}(\mathfrak {g}){\otimes } \mathscr {W}_{\ell }(\mathfrak {g})$-modules.
Corollary 8.8. Let ![]() $\mathfrak {g}$ be simply laced. Let
$\mathfrak {g}$ be simply laced. Let ![]() $k+h^{\vee }=(2h^{\vee }+1)/h^{\vee }$ so that
$k+h^{\vee }=(2h^{\vee }+1)/h^{\vee }$ so that ![]() $\ell +h^{\vee }=(2h^{\vee }+1)/(h^{\vee }+1)$.
$\ell +h^{\vee }=(2h^{\vee }+1)/(h^{\vee }+1)$.
1. There is an embedding of vertex algebras
and $$ \begin{align*} \mathscr{W}_{k}(\mathfrak{g}){\otimes} \mathscr{W}_{\ell}(\mathfrak{g})\hookrightarrow \mathbb{L}_{1}(\mathfrak{g}), \end{align*} $$
$$ \begin{align*} \mathscr{W}_{k}(\mathfrak{g}){\otimes} \mathscr{W}_{\ell}(\mathfrak{g})\hookrightarrow \mathbb{L}_{1}(\mathfrak{g}), \end{align*} $$ $\mathscr {W}_{k}(\mathfrak {g})$ and
$\mathscr {W}_{k}(\mathfrak {g})$ and  $ \mathscr {W}_{\ell }(\mathfrak {g})$ form a dual pair in
$ \mathscr {W}_{\ell }(\mathfrak {g})$ form a dual pair in  $ \mathbb {L}_{1}(\mathfrak {g})$.
$ \mathbb {L}_{1}(\mathfrak {g})$.2. For
 $\nu \in P^{1}_{+}$, we have as
$\nu \in P^{1}_{+}$, we have as $$ \begin{align*} \mathbb{L}^{1}_{\nu}\cong \bigoplus_{\lambda\in Adm_{\mathbb{Z}}^{k}\cap (\nu+Q)} \mathbf{L}_{[\lambda,0]}^{k}\otimes \mathbf{L}_{[\lambda,0]}^{\ell} \end{align*} $$
$$ \begin{align*} \mathbb{L}^{1}_{\nu}\cong \bigoplus_{\lambda\in Adm_{\mathbb{Z}}^{k}\cap (\nu+Q)} \mathbf{L}_{[\lambda,0]}^{k}\otimes \mathbf{L}_{[\lambda,0]}^{\ell} \end{align*} $$ $\mathscr {W}_{k}(\mathfrak {g}){\otimes } \mathscr {W}_{\ell }(\mathfrak {g})$-modules.
$\mathscr {W}_{k}(\mathfrak {g}){\otimes } \mathscr {W}_{\ell }(\mathfrak {g})$-modules.
Proof. The assertion follows from Theorem 8.7 noting that ![]() $\mathscr {W}_{k-1}(\mathfrak {g})=\mathbf {L}_{[0,0]}^{k-1}=\mathbb {C}$ if
$\mathscr {W}_{k-1}(\mathfrak {g})=\mathbf {L}_{[0,0]}^{k-1}=\mathbb {C}$ if ![]() $k+h^{\vee }-1=(h^{\vee }+1)/h^{\vee }$ or
$k+h^{\vee }-1=(h^{\vee }+1)/h^{\vee }$ or ![]() $h^{\vee }/(h^{\vee }+1)$.
$h^{\vee }/(h^{\vee }+1)$.
Proof of Theorem 8.6 and Theorem 8.7.
By [Reference Arakawa, Creutzig and LinshawACL19, Main Theorem 3], we have
 $$ \begin{align*} \mathbb{L}^{k-1}_{\mu}\otimes \mathbb{L}^{1}_{\nu}\cong \bigoplus_{\lambda\in Adm^{k}_{\mathbb{Z}}\atop \lambda-\mu-\nu\in Q} \mathbb{L}^{k}_{\lambda}\otimes \mathbf{L}_{[\lambda,\mu]}^{\ell} \end{align*} $$
$$ \begin{align*} \mathbb{L}^{k-1}_{\mu}\otimes \mathbb{L}^{1}_{\nu}\cong \bigoplus_{\lambda\in Adm^{k}_{\mathbb{Z}}\atop \lambda-\mu-\nu\in Q} \mathbb{L}^{k}_{\lambda}\otimes \mathbf{L}_{[\lambda,\mu]}^{\ell} \end{align*} $$as ![]() $\mathbb {L}_{k}(\mathfrak {g}){\otimes } \mathscr {W}_{\ell }(\mathfrak {g})$-modules. Hence, the assertion follows from Main Theorem 1 and Theorem 7.1.
$\mathbb {L}_{k}(\mathfrak {g}){\otimes } \mathscr {W}_{\ell }(\mathfrak {g})$-modules. Hence, the assertion follows from Main Theorem 1 and Theorem 7.1.
9 Application to the extension problem of vertex algebras
In this section, we apply Theorem 8.2 to prove the existence of the extensions of vertex algebras that are expected by four-dimensional supersymmetric gauge theories ([Reference Creutzig and GaiottoCG17, Reference Creutzig, Gaiotto and LinshawCGL18]).
For ![]() $\lambda \in P_{+}$, let
$\lambda \in P_{+}$, let ![]() $\lambda ^{*}=-w_{0}(\lambda )$ so that
$\lambda ^{*}=-w_{0}(\lambda )$ so that ![]() $E_{\lambda }^{*}\cong E_{\lambda ^{*}}$.
$E_{\lambda }^{*}\cong E_{\lambda ^{*}}$.
Theorem 9.1. Let ![]() $\mathfrak {g}$ be simply laced, and let
$\mathfrak {g}$ be simply laced, and let ![]() $k, k^{\prime }$ be irrational complex numbers satisfying
$k, k^{\prime }$ be irrational complex numbers satisfying
for ![]() $n\in \mathbb {Z}_{\geqslant 1}$. Then
$n\in \mathbb {Z}_{\geqslant 1}$. Then
can be equipped with a structure of simple vertex operator algebra of central charge
 $$ \begin{align*} 2\operatorname{rk}\mathfrak{g}+4h \dim \mathfrak{g}- n h \dim \mathfrak{g} \left(1 + \frac{\psi^{2}}{n \psi-1} \right), \end{align*} $$
$$ \begin{align*} 2\operatorname{rk}\mathfrak{g}+4h \dim \mathfrak{g}- n h \dim \mathfrak{g} \left(1 + \frac{\psi^{2}}{n \psi-1} \right), \end{align*} $$where ![]() $\psi = k+h^{\vee }$ and h is the Coxeter number (which equals to
$\psi = k+h^{\vee }$ and h is the Coxeter number (which equals to ![]() $h^{\vee }$). The vertex operator algebra
$h^{\vee }$). The vertex operator algebra ![]() $A^{n}[\mathfrak {g}]$ is of CFT type if
$A^{n}[\mathfrak {g}]$ is of CFT type if ![]() $n\geqslant 2$.
$n\geqslant 2$.
Proof. We shall prove the assertion on induction on n using the fact that
 $$ \begin{align} T^{k^{\prime}}_{\mu,\mu^{\prime}}{\otimes}\mathcal{U}(\mathfrak{g})\cong \bigoplus_{\lambda\in P_{+}\atop \lambda-\mu-\mu^{\prime}\in Q} T^{k^{\prime}+1}_{\lambda,\mu^{\prime}}{\otimes} T^{\ell}_{\lambda,\mu} \cong \bigoplus_{\lambda\in P_{+}\atop \lambda-\mu-\mu^{\prime}\in Q} T^{k^{\prime}+1}_{\lambda,\mu^{\prime}}{\otimes} T^{\check{\ell}}_{\mu,\lambda}, \end{align} $$
$$ \begin{align} T^{k^{\prime}}_{\mu,\mu^{\prime}}{\otimes}\mathcal{U}(\mathfrak{g})\cong \bigoplus_{\lambda\in P_{+}\atop \lambda-\mu-\mu^{\prime}\in Q} T^{k^{\prime}+1}_{\lambda,\mu^{\prime}}{\otimes} T^{\ell}_{\lambda,\mu} \cong \bigoplus_{\lambda\in P_{+}\atop \lambda-\mu-\mu^{\prime}\in Q} T^{k^{\prime}+1}_{\lambda,\mu^{\prime}}{\otimes} T^{\check{\ell}}_{\mu,\lambda}, \end{align} $$with ![]() $\check {\ell }$ satisfying the relation
$\check {\ell }$ satisfying the relation
which follows from Theorem 8.2 and equation (44).
Let us show the assertion for ![]() $n=1$. Let
$n=1$. Let ![]() $\mathbf {I}_{G}^{k}$ be the chiral universal centralizer on G at level k ([Reference ArakawaAra18]), which was introduced earlier in [Reference Frenkel and StyrkasFS06] for the
$\mathbf {I}_{G}^{k}$ be the chiral universal centralizer on G at level k ([Reference ArakawaAra18]), which was introduced earlier in [Reference Frenkel and StyrkasFS06] for the ![]() $\mathfrak {g}=\mathfrak {sl}_{2}$ case as the modified regular representation of the Virasoro algebra. By definition,
$\mathfrak {g}=\mathfrak {sl}_{2}$ case as the modified regular representation of the Virasoro algebra. By definition, ![]() $\mathbf {I}_{G}^{k}$ is obtained by taking the principal Drinfeld–Sokolov reduction with respect to two commuting actions of
$\mathbf {I}_{G}^{k}$ is obtained by taking the principal Drinfeld–Sokolov reduction with respect to two commuting actions of ![]() $\widehat {\mathfrak {g}}$ on the algebra of the chiral differential operators [Reference Malikov, Schechtman and VaintrobMSV99, Reference Beilinson and DrinfeldBD04]
$\widehat {\mathfrak {g}}$ on the algebra of the chiral differential operators [Reference Malikov, Schechtman and VaintrobMSV99, Reference Beilinson and DrinfeldBD04] ![]() $\mathcal {D}_{G,k}^{ch}$ on G at level k. The
$\mathcal {D}_{G,k}^{ch}$ on G at level k. The ![]() $\mathbf {I}_{G}^{k}$ is a conformal vertex algebra of central charge
$\mathbf {I}_{G}^{k}$ is a conformal vertex algebra of central charge ![]() $2 \operatorname {rk}\mathfrak {g} + 48(\rho |\rho ^{\vee }) =2 \operatorname {rk}\mathfrak {g}+4 h^{\vee }\dim \mathfrak {g}$, equipped with a conformal vertex algebra homomorphism
$2 \operatorname {rk}\mathfrak {g} + 48(\rho |\rho ^{\vee }) =2 \operatorname {rk}\mathfrak {g}+4 h^{\vee }\dim \mathfrak {g}$, equipped with a conformal vertex algebra homomorphism ![]() $\mathscr {W}^{k}(\mathfrak {g}){\otimes } \mathscr {W}^{k^{*}}(\mathfrak {g})\rightarrow \mathbf {I}_{G}^{k}$, where
$\mathscr {W}^{k}(\mathfrak {g}){\otimes } \mathscr {W}^{k^{*}}(\mathfrak {g})\rightarrow \mathbf {I}_{G}^{k}$, where ![]() $k^{*}$ the dual level of k defined by the equation
$k^{*}$ the dual level of k defined by the equation
As explained in [Reference ArakawaAra18], ![]() $\mathbf {I}_{G}^{k}$ is a strict chiral quantization ([Reference ArakawaAra18]) of the universal centralizer
$\mathbf {I}_{G}^{k}$ is a strict chiral quantization ([Reference ArakawaAra18]) of the universal centralizer ![]() $\mathcal {S}\times _{\mathfrak {g}^{*}}(G\times \mathcal {S})$, where
$\mathcal {S}\times _{\mathfrak {g}^{*}}(G\times \mathcal {S})$, where ![]() $ \mathcal {S}$ is the Kostant–Slodowy slice. Since
$ \mathcal {S}$ is the Kostant–Slodowy slice. Since ![]() $\mathcal {S}\times _{\mathfrak {g}^{*}}(G\times \mathcal {S})$ is a smooth symplectic variety,
$\mathcal {S}\times _{\mathfrak {g}^{*}}(G\times \mathcal {S})$ is a smooth symplectic variety, ![]() $\mathbf {I}_{G}^{k}$ is simple ([Reference Arakawa and MoreauAM]). For an irrational k, we have the decomposition
$\mathbf {I}_{G}^{k}$ is simple ([Reference Arakawa and MoreauAM]). For an irrational k, we have the decomposition
as ![]() $\mathscr {W}^{k}(\mathfrak {g}){\otimes } \mathscr {W}^{k^{*}}(\mathfrak {g})$-modules, which follows from the decomposition [Reference Arkhipov and GaitsgoryAG02, Reference ZhuZhu08] of
$\mathscr {W}^{k}(\mathfrak {g}){\otimes } \mathscr {W}^{k^{*}}(\mathfrak {g})$-modules, which follows from the decomposition [Reference Arkhipov and GaitsgoryAG02, Reference ZhuZhu08] of ![]() $\mathcal {D}_{G,k}^{ch}$ as
$\mathcal {D}_{G,k}^{ch}$ as ![]() $\widehat {\mathfrak {g}}\times \widehat {\mathfrak {g}}$-modules. Hence, by equation (60),
$\widehat {\mathfrak {g}}\times \widehat {\mathfrak {g}}$-modules. Hence, by equation (60),
 $$ \begin{align*} \mathbf{I}_{G}^{k}{\otimes} \mathcal{U}(\mathfrak{g}) \cong \bigoplus_{\lambda\in P_{+}}T_{\lambda,0}^{k}{\otimes} T_{\lambda^{*},0}^{k^{*}}{\otimes} \mathcal{U}(\mathfrak{g}) \cong \bigoplus_{\lambda\in P_{+}, \ \mu\in P_{+} \atop \mu-\lambda^{*}\in Q}T_{\lambda,0}^{k} {\otimes} T_{\mu,0}^{k^{*}+1}{\otimes} T_{\lambda^{*},\mu}^{\check{\ell}}, \end{align*} $$
$$ \begin{align*} \mathbf{I}_{G}^{k}{\otimes} \mathcal{U}(\mathfrak{g}) \cong \bigoplus_{\lambda\in P_{+}}T_{\lambda,0}^{k}{\otimes} T_{\lambda^{*},0}^{k^{*}}{\otimes} \mathcal{U}(\mathfrak{g}) \cong \bigoplus_{\lambda\in P_{+}, \ \mu\in P_{+} \atop \mu-\lambda^{*}\in Q}T_{\lambda,0}^{k} {\otimes} T_{\mu,0}^{k^{*}+1}{\otimes} T_{\lambda^{*},\mu}^{\check{\ell}}, \end{align*} $$and ![]() $\check {\ell }$ satisfies the relation
$\check {\ell }$ satisfies the relation
It follows that
 $$ \begin{align*} {A}^{1}[\mathfrak{g}]:=\operatorname{Com}(\mathscr{W}^{k^{*}+1}(\mathfrak{g}), \mathbf{I}_{G}^{k}{\otimes}\mathcal{U}(\mathfrak{g})) \cong \bigoplus_{\lambda\in P_{+}\cap Q}T^{k}_{\lambda,0}{\otimes} T^{\check{\ell}}_{\lambda^{*},0}. \end{align*} $$
$$ \begin{align*} {A}^{1}[\mathfrak{g}]:=\operatorname{Com}(\mathscr{W}^{k^{*}+1}(\mathfrak{g}), \mathbf{I}_{G}^{k}{\otimes}\mathcal{U}(\mathfrak{g})) \cong \bigoplus_{\lambda\in P_{+}\cap Q}T^{k}_{\lambda,0}{\otimes} T^{\check{\ell}}_{\lambda^{*},0}. \end{align*} $$Moreover, since ![]() $\mathbf {I}_{G}^{k}{\otimes } \mathcal {U}(\mathfrak {g})$ is simple
$\mathbf {I}_{G}^{k}{\otimes } \mathcal {U}(\mathfrak {g})$ is simple ![]() ${A}^{1}[\mathfrak {g}]$ is simple as well by [Reference Creutzig, Genra and NakatsukaCGN, Proposition 5.4].
${A}^{1}[\mathfrak {g}]$ is simple as well by [Reference Creutzig, Genra and NakatsukaCGN, Proposition 5.4].
Assuming that the statement is true for ![]() $n\in \mathbb {Z}_{\geqslant 1}$, we find similarly that
$n\in \mathbb {Z}_{\geqslant 1}$, we find similarly that
has the required decomposition.
For the central charge computation, it is useful to introduce
so that
By equation (34) and the fact that the central charge of ![]() $\mathscr {W}^{k+1}(\mathfrak {g})$ is
$\mathscr {W}^{k+1}(\mathfrak {g})$ is
 $$ \begin{align*} (1-h(h+1)(k+h)^{2}/(k+h+1))\operatorname{rk}\mathfrak{g} = \operatorname{rk}\mathfrak{g} - \dim \mathfrak{g} h \frac{\psi^{2}}{\psi +1} \end{align*} $$
$$ \begin{align*} (1-h(h+1)(k+h)^{2}/(k+h+1))\operatorname{rk}\mathfrak{g} = \operatorname{rk}\mathfrak{g} - \dim \mathfrak{g} h \frac{\psi^{2}}{\psi +1} \end{align*} $$(here we used that ![]() $ (h+1) \operatorname {rk} \mathfrak {g} = \dim \mathfrak {g}$), we have
$ (h+1) \operatorname {rk} \mathfrak {g} = \dim \mathfrak {g}$), we have
 $$ \begin{align*} \begin{aligned} c_{A^{n+1}[\mathfrak{g}]} &= c_{A^{n}[\mathfrak{g}]}-\frac{h^{2}+h-1}{h+1}\dim \mathfrak{g} - \operatorname{rk}\mathfrak{g} + h\frac{\psi^{2}}{(n\psi-1)((n+1)\psi-1)})\dim\mathfrak{g} \\ &= - \dim \mathfrak{g} h + h \phi_{n} \phi_{n+1}\dim\mathfrak{g}, \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} c_{A^{n+1}[\mathfrak{g}]} &= c_{A^{n}[\mathfrak{g}]}-\frac{h^{2}+h-1}{h+1}\dim \mathfrak{g} - \operatorname{rk}\mathfrak{g} + h\frac{\psi^{2}}{(n\psi-1)((n+1)\psi-1)})\dim\mathfrak{g} \\ &= - \dim \mathfrak{g} h + h \phi_{n} \phi_{n+1}\dim\mathfrak{g}, \end{aligned} \end{align*} $$where ![]() $c_{V}$ is the central charge of V, and we have put
$c_{V}$ is the central charge of V, and we have put ![]() $A^{0}[\mathfrak {g}]=\mathbf {I}_{G}^{k}$. Note that
$A^{0}[\mathfrak {g}]=\mathbf {I}_{G}^{k}$. Note that
and so by induction for n, we have
The conformal dimension of ![]() $T_{\lambda ,0}^{k}{\otimes } T_{\lambda ^{*},0}^{k^{\prime }}$ is
$T_{\lambda ,0}^{k}{\otimes } T_{\lambda ^{*},0}^{k^{\prime }}$ is
which is an integer for ![]() $\lambda \in Q$. If
$\lambda \in Q$. If ![]() $n\geqslant 2$, this is clearly nonnegative and is equal to zero if and only if
$n\geqslant 2$, this is clearly nonnegative and is equal to zero if and only if ![]() $\lambda =0$, whence the last assertion.
$\lambda =0$, whence the last assertion.
Remark 9.2. More generally, it is expected [Reference Creutzig and GaiottoCG17, Reference Creutzig, Gaiotto and LinshawCGL18] that if k and ![]() $k^{\prime }$ are irrational numbers related by
$k^{\prime }$ are irrational numbers related by
then
can be given the structure of a simple vertex operator algebra for any nilpotent elements f, ![]() $f^{\prime }$.
$f^{\prime }$.
10 Fusion categories of modules over quasi-lisse W-algebras
For a vertex operator algebra V, let ![]() $\mathcal {C}_{V}^{ord}$ be the full subcategory of the category of finitely generated V-modules consisting of modules M on which
$\mathcal {C}_{V}^{ord}$ be the full subcategory of the category of finitely generated V-modules consisting of modules M on which ![]() $L_{0}$ acts locally finitely, the
$L_{0}$ acts locally finitely, the ![]() $L_{0}$-eigenvalues of M are bounded from below and all the generalized
$L_{0}$-eigenvalues of M are bounded from below and all the generalized ![]() $L_{0}$-eigenspaces are finite dimensional. A simple object in
$L_{0}$-eigenspaces are finite dimensional. A simple object in ![]() $\mathcal {C}_{V}^{ord}$ is called an ordinary representation of V.
$\mathcal {C}_{V}^{ord}$ is called an ordinary representation of V.
Recall that a finitely strongly generated vertex algebra V is called quasi-lisse [Reference Arakawa and KawasetsuAK18] if the associate variety ![]() $X_{V}$ has finitely many symplectic leaves. By [Reference Arakawa and KawasetsuAK18, Theorem 4.1], if V is quasi-lisse, then
$X_{V}$ has finitely many symplectic leaves. By [Reference Arakawa and KawasetsuAK18, Theorem 4.1], if V is quasi-lisse, then ![]() $\mathcal {C}_{V}^{ord}$ has only finitely many simple objects.
$\mathcal {C}_{V}^{ord}$ has only finitely many simple objects.
Conjecture 1. Let V a finitely strongly generated, self-dual, quasi-lisse vertex operator algebra of CFT type. Then the category ![]() $\mathcal {C}_{V}^{ord}$ has the structure of a vertex tensor category in the sense of [Reference Huang and LepowskyHL94].
$\mathcal {C}_{V}^{ord}$ has the structure of a vertex tensor category in the sense of [Reference Huang and LepowskyHL94].
In the case that V is lisse, that is, ![]() $X_{V}$ is zero dimensional, Conjecture 1 has been proved in [Reference HuangHua09]. Conjecture 1 is true if one can show that every object in
$X_{V}$ is zero dimensional, Conjecture 1 has been proved in [Reference HuangHua09]. Conjecture 1 is true if one can show that every object in ![]() $\mathcal {C}_{V}^{ord}$ is
$\mathcal {C}_{V}^{ord}$ is ![]() $C_{1}$-cofinite and if grading-restricted generalized Verma modules for V are of finite length [Reference Creutzig and YangCY20]. If V is a vertex algebra that has an affine vertex subalgebra at admissible level, then another possibility of proving Conjecture 1 is the following. First, show that the affine vertex subalgebra is simple; second, prove that a suitable category of modules of the coset by the affine subalgebra in V has vertex tensor category structure. Then use the theory of vertex algebra extensions [Reference Creutzig, Kanade and McRaeCKM17] to deduce vertex tensor category structure on
$C_{1}$-cofinite and if grading-restricted generalized Verma modules for V are of finite length [Reference Creutzig and YangCY20]. If V is a vertex algebra that has an affine vertex subalgebra at admissible level, then another possibility of proving Conjecture 1 is the following. First, show that the affine vertex subalgebra is simple; second, prove that a suitable category of modules of the coset by the affine subalgebra in V has vertex tensor category structure. Then use the theory of vertex algebra extensions [Reference Creutzig, Kanade and McRaeCKM17] to deduce vertex tensor category structure on ![]() $\mathcal {C}_{V}^{ord}$. This is a promising direction as, for example, many simple quotients of cosets of
$\mathcal {C}_{V}^{ord}$. This is a promising direction as, for example, many simple quotients of cosets of ![]() $\mathcal W$-algebras of type A are rational and lisse by [Reference Creutzig and LinshawCL20, Cor. 6.13], and similar results for
$\mathcal W$-algebras of type A are rational and lisse by [Reference Creutzig and LinshawCL20, Cor. 6.13], and similar results for ![]() $\mathcal W$-algebras of type
$\mathcal W$-algebras of type ![]() $B, C$ and D are work in progress.
$B, C$ and D are work in progress.
In the case that Conjecture 1 is true, we denote by ![]() $M\boxtimes _{V} N$ the tensor product of V-modules M and N in
$M\boxtimes _{V} N$ the tensor product of V-modules M and N in ![]() $\mathcal {C}_{V}^{ord}$, or simply by
$\mathcal {C}_{V}^{ord}$, or simply by ![]() $M\boxtimes N$ if no confusion should occur.
$M\boxtimes N$ if no confusion should occur.
Now let k be an admissible number for ![]() $\widehat {\mathfrak {g}}$. As explained in Subsection 8.2,
$\widehat {\mathfrak {g}}$. As explained in Subsection 8.2,
for some nilpotent orbit ![]() $\mathbb {O}_{k}$, and hence,
$\mathbb {O}_{k}$, and hence, ![]() $\mathbb {L}_{k}(\mathfrak {g})$ is quasi-lisse. By the conjecture of Adamović and Milas [Reference Adamović and MilasAM95] that was proved in [Reference ArakawaAra16a], the category
$\mathbb {L}_{k}(\mathfrak {g})$ is quasi-lisse. By the conjecture of Adamović and Milas [Reference Adamović and MilasAM95] that was proved in [Reference ArakawaAra16a], the category ![]() $C_{\mathbb {L}_{k}(\mathfrak {g})}^{ord}$ is semisimple and
$C_{\mathbb {L}_{k}(\mathfrak {g})}^{ord}$ is semisimple and ![]() $\{ \mathbb {L}^{k}_{\lambda } | \lambda \in Adm^{k}_{\mathbb {Z}}\}$ gives a complete set of isomorphism classes in
$\{ \mathbb {L}^{k}_{\lambda } | \lambda \in Adm^{k}_{\mathbb {Z}}\}$ gives a complete set of isomorphism classes in ![]() $\mathcal {C}_{\mathbb {L}_{k}(\mathfrak {g})}^{ord}$. Note that, in the case k is nonnegative integer, this is a well-known fact [Reference Frenkel and ZhuFZ92], and if this is the case,
$\mathcal {C}_{\mathbb {L}_{k}(\mathfrak {g})}^{ord}$. Note that, in the case k is nonnegative integer, this is a well-known fact [Reference Frenkel and ZhuFZ92], and if this is the case, ![]() $\mathbb {L}_{k}(\mathfrak {g})$ is rational and lisse, and hence, Conjecture 1 holds by [Reference Huang and LepowskyHL95]. In the case k is admissible but not an integer,
$\mathbb {L}_{k}(\mathfrak {g})$ is rational and lisse, and hence, Conjecture 1 holds by [Reference Huang and LepowskyHL95]. In the case k is admissible but not an integer, ![]() $\mathbb {L}_{k}(\mathfrak {g})$ is neither rational nor lisse anymore. Nevertheless, Conjecture 1 has been proved for
$\mathbb {L}_{k}(\mathfrak {g})$ is neither rational nor lisse anymore. Nevertheless, Conjecture 1 has been proved for ![]() $V=\mathbb {L}_{k}(\mathfrak {g})$ in [Reference Creutzig, Huang and YangCHY18] provided that
$V=\mathbb {L}_{k}(\mathfrak {g})$ in [Reference Creutzig, Huang and YangCHY18] provided that ![]() $\mathfrak {g}$ is simply laced. Moreover, it was shown in [Reference CreutzigCre19] that
$\mathfrak {g}$ is simply laced. Moreover, it was shown in [Reference CreutzigCre19] that ![]() $\mathcal {C}_{\mathbb {L}_{k}(\mathfrak {g})}^{ord}$ is a fusion category, i.e., any object is rigid, and we have an isomorphism
$\mathcal {C}_{\mathbb {L}_{k}(\mathfrak {g})}^{ord}$ is a fusion category, i.e., any object is rigid, and we have an isomorphism
of Grothendieck rings of our fusion categories, where p is the numerator of ![]() $k+h^{\vee }$.
$k+h^{\vee }$.
Let f be a nilpotent element of ![]() $\mathfrak {g}$. By [Reference ArakawaAra15a],
$\mathfrak {g}$. By [Reference ArakawaAra15a],
where ![]() $\mathcal {S}_{f}$ is the Slodowy slice at f in
$\mathcal {S}_{f}$ is the Slodowy slice at f in ![]() $\mathfrak {g}$. Therefore, in the case that k is admissible,
$\mathfrak {g}$. Therefore, in the case that k is admissible, ![]() $X_{H_{DS,f}^{0}(\mathbb {L}_{k}(\mathfrak {g}))}=\overline {\mathbb {O}_{k}}\cap \mathcal {S}_{f}$ is a nilpotent Slodowy slice, that is, the intersection of the Slodowy slice with a nilpotent orbit closure, provided that
$X_{H_{DS,f}^{0}(\mathbb {L}_{k}(\mathfrak {g}))}=\overline {\mathbb {O}_{k}}\cap \mathcal {S}_{f}$ is a nilpotent Slodowy slice, that is, the intersection of the Slodowy slice with a nilpotent orbit closure, provided that ![]() $H_{DS,f}^{0}(\mathbb {L}_{k}(\mathfrak {g}))\ne 0$ or, equivalently,
$H_{DS,f}^{0}(\mathbb {L}_{k}(\mathfrak {g}))\ne 0$ or, equivalently, ![]() $\overline {\mathbb {O}_{k}}\cap \mathcal {S}_{f}\ne \emptyset $, that is,
$\overline {\mathbb {O}_{k}}\cap \mathcal {S}_{f}\ne \emptyset $, that is, ![]() $f\in \overline {\mathbb {O}_{k}}$. In particular,
$f\in \overline {\mathbb {O}_{k}}$. In particular, ![]() $H_{DS,f}^{0}(\mathbb {L}_{k}(\mathfrak {g}))$ is quasi-lisse if
$H_{DS,f}^{0}(\mathbb {L}_{k}(\mathfrak {g}))$ is quasi-lisse if ![]() $f\in \overline {\mathbb {O}_{k}}$ and so is the simple W-algebra
$f\in \overline {\mathbb {O}_{k}}$ and so is the simple W-algebra ![]() $\mathscr {W}_{k}(\mathfrak {g},f)$. If
$\mathscr {W}_{k}(\mathfrak {g},f)$. If ![]() $f\in \mathbb {O}_{k}$, then
$f\in \mathbb {O}_{k}$, then ![]() $\overline {\mathbb {O}_{k}}\cap \mathcal {S}_{f}$ is a point by the transversality of the Slodowy slices, and therefore,
$\overline {\mathbb {O}_{k}}\cap \mathcal {S}_{f}$ is a point by the transversality of the Slodowy slices, and therefore, ![]() $\mathscr {W}_{k}(\mathfrak {g},f)$ is lisse.
$\mathscr {W}_{k}(\mathfrak {g},f)$ is lisse.
The good grading (11) is called even of ![]() $\mathfrak {g}_{j}=0$ unless
$\mathfrak {g}_{j}=0$ unless ![]() $j\in \mathbb {Z}$. If this is the case,
$j\in \mathbb {Z}$. If this is the case, ![]() $\mathscr {W}^{k}(\mathfrak {g},f)$ is
$\mathscr {W}^{k}(\mathfrak {g},f)$ is ![]() $\mathbb {Z}_{\geqslant 0}$-graded and thus of CFT type.
$\mathbb {Z}_{\geqslant 0}$-graded and thus of CFT type.
The following assertion was stated in the case that ![]() $f\in \mathbb {O}_{k}$ in [Reference Arakawa and van EkerenAvE], but the same proof applies.
$f\in \mathbb {O}_{k}$ in [Reference Arakawa and van EkerenAvE], but the same proof applies.
Theorem 10.1. Let k be admissible and ![]() $f\in \overline {\mathbb {O}}_{k}$. Suppose that f admits a good even grading. Then, for
$f\in \overline {\mathbb {O}}_{k}$. Suppose that f admits a good even grading. Then, for ![]() $\lambda \in Adm^{k}_{\mathbb {Z}}$,
$\lambda \in Adm^{k}_{\mathbb {Z}}$, ![]() $\mathbb {L}^{k}_{\lambda ,f}=H_{DS,f}^{0}(\mathbb {L}^{k}_{\lambda })$ is simple. In particular,
$\mathbb {L}^{k}_{\lambda ,f}=H_{DS,f}^{0}(\mathbb {L}^{k}_{\lambda })$ is simple. In particular, ![]() $H_{DS,f}^{0}(\mathbb {L}_{k}(\mathfrak {g}))=\mathscr {W}_{k}(\mathfrak {g},f)$.
$H_{DS,f}^{0}(\mathbb {L}_{k}(\mathfrak {g}))=\mathscr {W}_{k}(\mathfrak {g},f)$.
Lemma 10.2. Let f be an even nilpotent element. Then ![]() $\mathscr {W}_{k}(\mathfrak {g},f)$ is self-dual and of CFT type with respect to the Dynkin grading.
$\mathscr {W}_{k}(\mathfrak {g},f)$ is self-dual and of CFT type with respect to the Dynkin grading.
Proof. Since f is an even nilpotent element, the Dynkin grading is even, and so ![]() $\mathscr {W}_{k}(\mathfrak {g},f)$ is of CFT type. The self-duality follows from the formula in [Reference Arakawa and van EkerenAvE, Proposition 6.1].
$\mathscr {W}_{k}(\mathfrak {g},f)$ is of CFT type. The self-duality follows from the formula in [Reference Arakawa and van EkerenAvE, Proposition 6.1].
Remark 10.3. If the grading is not Dynkin, ![]() $\mathscr {W}_{k}(f,g)$ need not be self-dual; see [Reference Arakawa and van EkerenAvE, Proposition 6.3].
$\mathscr {W}_{k}(f,g)$ need not be self-dual; see [Reference Arakawa and van EkerenAvE, Proposition 6.3].
Theorem 10.4. Let ![]() $\mathfrak {g}$ be simply laced, k admissible, and let f be an even nilpotent element in
$\mathfrak {g}$ be simply laced, k admissible, and let f be an even nilpotent element in ![]() $\overline {\mathbb {O}}_{k}$. Suppose Conjecture 1 is true for
$\overline {\mathbb {O}}_{k}$. Suppose Conjecture 1 is true for ![]() $\mathscr {W}_{k+1}(\mathfrak {g},f)$ and also that
$\mathscr {W}_{k+1}(\mathfrak {g},f)$ and also that ![]() $\mathscr {W}_{k+1}(\mathfrak {g},f)$ is self-dual. Then the functor
$\mathscr {W}_{k+1}(\mathfrak {g},f)$ is self-dual. Then the functor
is a unital braided tensor functor. In particular, the modules ![]() $\mathbb {L}^{k}_{\lambda ,f}$,
$\mathbb {L}^{k}_{\lambda ,f}$, ![]() $\lambda \in Adm^{k}_{\mathbb {Z}}$, are rigid.
$\lambda \in Adm^{k}_{\mathbb {Z}}$, are rigid.
Remark 10.5. Note that by Theorem 8.6, we have that ![]() $\mathscr {W}_{k}(\mathfrak {g},f) \otimes \mathbb {L}_{1}(\mathfrak {g})$ is an extension of
$\mathscr {W}_{k}(\mathfrak {g},f) \otimes \mathbb {L}_{1}(\mathfrak {g})$ is an extension of ![]() $\mathscr {W}_{k+1}(\mathfrak {g},f) \otimes \mathscr {W}_{\ell }(\mathfrak {g})$, where
$\mathscr {W}_{k+1}(\mathfrak {g},f) \otimes \mathscr {W}_{\ell }(\mathfrak {g})$, where ![]() $\mathscr {W}_{\ell }(\mathfrak {g})$ is rational and lisse if k is admissible. Especially every ordinary module of
$\mathscr {W}_{\ell }(\mathfrak {g})$ is rational and lisse if k is admissible. Especially every ordinary module of ![]() $\mathscr {W}_{k}(\mathfrak {g},f) \otimes \mathbb {L}_{1}(\mathfrak {g})$ is an object in the category of ordinary modules of
$\mathscr {W}_{k}(\mathfrak {g},f) \otimes \mathbb {L}_{1}(\mathfrak {g})$ is an object in the category of ordinary modules of ![]() $\mathscr {W}_{k+1}(\mathfrak {g},f) \otimes \mathscr {W}_{\ell }(\mathfrak {g})$, and so if the latter has vertex tensor category structure, then so does the former by [Reference Creutzig, Kanade and McRaeCKM17]. In other words, if Conjecture 1 is true for
$\mathscr {W}_{k+1}(\mathfrak {g},f) \otimes \mathscr {W}_{\ell }(\mathfrak {g})$, and so if the latter has vertex tensor category structure, then so does the former by [Reference Creutzig, Kanade and McRaeCKM17]. In other words, if Conjecture 1 is true for ![]() $\mathscr {W}_{k+1}(\mathfrak {g},f)$ and if k is admissible, then Conjecture 1 is also true for
$\mathscr {W}_{k+1}(\mathfrak {g},f)$ and if k is admissible, then Conjecture 1 is also true for ![]() $\mathscr {W}_{k}(\mathfrak {g},f)$.
$\mathscr {W}_{k}(\mathfrak {g},f)$.
Moreover, [Reference Creutzig, Kanade and McRaeCKM19, Thm. 5.12] applies to our setting if ![]() $\mathscr {W}_{k}(\mathfrak {g},f)$ is
$\mathscr {W}_{k}(\mathfrak {g},f)$ is ![]() $\mathbb Z$-graded. Thus, if the category of ordinary modules of
$\mathbb Z$-graded. Thus, if the category of ordinary modules of ![]() $\mathscr {W}_{k+1}(\mathfrak {g},f) \otimes \mathscr {W}_{\ell }(\mathfrak {g})$ is a fusion category, then so is the one of
$\mathscr {W}_{k+1}(\mathfrak {g},f) \otimes \mathscr {W}_{\ell }(\mathfrak {g})$ is a fusion category, then so is the one of ![]() $\mathscr {W}_{k}(\mathfrak {g},f) \otimes \mathbb {L}_{1}(\mathfrak {g})$. If
$\mathscr {W}_{k}(\mathfrak {g},f) \otimes \mathbb {L}_{1}(\mathfrak {g})$. If ![]() $\mathscr {W}_{k}(\mathfrak {g},f)$ is
$\mathscr {W}_{k}(\mathfrak {g},f)$ is ![]() $\mathbb Z$-graded by conformal weight, it thus also follows that
$\mathbb Z$-graded by conformal weight, it thus also follows that ![]() $\mathscr {W}_{k}(\mathfrak {g},f)$ is rational provided that
$\mathscr {W}_{k}(\mathfrak {g},f)$ is rational provided that ![]() $\mathscr {W}_{k+1}(\mathfrak {g},f)$ is rational and lisse.
$\mathscr {W}_{k+1}(\mathfrak {g},f)$ is rational and lisse.
Note that if ![]() $f\in \mathbb {O}_{k}$, then Conjecture 1 holds since
$f\in \mathbb {O}_{k}$, then Conjecture 1 holds since ![]() $\mathscr {W}_{k}(\mathfrak {g},f)$ is lisse.
$\mathscr {W}_{k}(\mathfrak {g},f)$ is lisse.
In the case that ![]() $f=f_{prin}$,
$f=f_{prin}$, ![]() $f\in \overline {\mathbb {O}}_{k}$ if and only if
$f\in \overline {\mathbb {O}}_{k}$ if and only if ![]() $\overline {\mathbb {O}}_{k}=\mathcal {N}$, the nilpotent cone of
$\overline {\mathbb {O}}_{k}=\mathcal {N}$, the nilpotent cone of ![]() $\mathfrak {g}$. An admissible number k such that
$\mathfrak {g}$. An admissible number k such that ![]() $\overline {\mathbb {O}}_{k}=\mathcal {N}$ is called nondegenerate. If this is the case,
$\overline {\mathbb {O}}_{k}=\mathcal {N}$ is called nondegenerate. If this is the case, ![]() $\mathscr {W}^{k}(\mathfrak {g})$ is rational, and the complete fusion rule
$\mathscr {W}^{k}(\mathfrak {g})$ is rational, and the complete fusion rule ![]() $\mathscr {W}_{k}(\mathfrak {g},f)$ has been determined previously in [Reference Frenkel, Kac and WakimotoFKW92, Reference Arakawa and van EkerenAvE19, Reference CreutzigCre19].
$\mathscr {W}_{k}(\mathfrak {g},f)$ has been determined previously in [Reference Frenkel, Kac and WakimotoFKW92, Reference Arakawa and van EkerenAvE19, Reference CreutzigCre19].
In the case that ![]() $\mathbb {O}_{k}$ is a subregular nilpotent orbit and
$\mathbb {O}_{k}$ is a subregular nilpotent orbit and ![]() $f\in \mathbb {O}_{k}$, then
$f\in \mathbb {O}_{k}$, then ![]() $\mathscr {W}_{k}(\mathfrak {g},f)$ is rational [Reference Arakawa and van EkerenAvE], and the fusion rules of
$\mathscr {W}_{k}(\mathfrak {g},f)$ is rational [Reference Arakawa and van EkerenAvE], and the fusion rules of ![]() $\mathscr {W}_{k}(\mathfrak {g},f)$ has been determined in [Reference Arakawa and van EkerenAvE].
$\mathscr {W}_{k}(\mathfrak {g},f)$ has been determined in [Reference Arakawa and van EkerenAvE].
The following assertion, which follows immediately from Theorem 10.4, is new except for type A ([Reference Arakawa and van EkerenAvE]) and the above cases since the conjectural rationality [Reference Kac and WakimotoKW08, Reference ArakawaAra15a] of ![]() $\mathscr {W}_{k}(\mathfrak {g},f)$ with
$\mathscr {W}_{k}(\mathfrak {g},f)$ with ![]() $f\in \mathbb {O}_{k}$ is open otherwise.
$f\in \mathbb {O}_{k}$ is open otherwise.
Corollary 10.6. Let ![]() $\mathfrak {g}$ be simply laced and k admissible, and suppose that
$\mathfrak {g}$ be simply laced and k admissible, and suppose that ![]() $\mathbb {O}_{k}$ is an even nilpotent orbit,
$\mathbb {O}_{k}$ is an even nilpotent orbit, ![]() $f\in \mathbb {O}_{k}$. Then
$f\in \mathbb {O}_{k}$. Then ![]() $\mathbb {L}^{k}_{\lambda ,f}$ is rigid for all
$\mathbb {L}^{k}_{\lambda ,f}$ is rigid for all ![]() $\lambda \in Adm^{k}_{\mathbb {Z}}$.
$\lambda \in Adm^{k}_{\mathbb {Z}}$.
Remark 10.7. Let ![]() $ \mathcal {C}_{\mathscr {W}_{k}(\mathfrak {g},f)}^{KL}$ denote the fusion category consisting of objects
$ \mathcal {C}_{\mathscr {W}_{k}(\mathfrak {g},f)}^{KL}$ denote the fusion category consisting of objects ![]() $H_{DS,f}^{0}(M)$,
$H_{DS,f}^{0}(M)$, ![]() $M\in \mathcal {C}_{\mathbb {L}_{k}(\mathfrak {g})}^{ord}$. By Theorem 10.4,
$M\in \mathcal {C}_{\mathbb {L}_{k}(\mathfrak {g})}^{ord}$. By Theorem 10.4,
is a quotient functor between fusion categories. It gives an equivalence if and only if the modules ![]() $\mathbb {L}^{k}_{\lambda ,f}$,
$\mathbb {L}^{k}_{\lambda ,f}$, ![]() $ \lambda \in Adm^{k}_{\mathbb {Z}}$ are distinct.
$ \lambda \in Adm^{k}_{\mathbb {Z}}$ are distinct.
The rest of this section is devoted to the proof of Theorem 10.4.
Suppose Conjecture 1 holds for V, and let ![]() $\mathcal C$ be a monoidal full subcategory of
$\mathcal C$ be a monoidal full subcategory of ![]() $\mathcal {C}_{V}^{ord}$. Recall that
$\mathcal {C}_{V}^{ord}$. Recall that ![]() $M, N\in \mathcal {C}$ are said to centralize each other [Reference MügerMü03] if the monodromy of M and N is trivial, i.e., is equal to the identity on
$M, N\in \mathcal {C}$ are said to centralize each other [Reference MügerMü03] if the monodromy of M and N is trivial, i.e., is equal to the identity on ![]() $M\boxtimes _{V} N$, where the monodromy is the double braiding
$M\boxtimes _{V} N$, where the monodromy is the double braiding
Suppose that V is a vertex operator subalgebra of another quasi-lisse vertex operator algebra W and that W as a V-module is an object of ![]() $\mathcal {C}_{V}^{ord}$. We assume that Conjecture 1 holds for W as well. Let
$\mathcal {C}_{V}^{ord}$. We assume that Conjecture 1 holds for W as well. Let ![]() $\mathcal {D}$ be a monoidal full subcategory of
$\mathcal {D}$ be a monoidal full subcategory of ![]() $\mathcal C$ such that W and any object in
$\mathcal C$ such that W and any object in ![]() $\mathcal {D}$ centralize each other. Then
$\mathcal {D}$ centralize each other. Then
can be equipped with a structure of a module for the vertex operator algebra W, giving rise to the induction functor [Reference Creutzig, Kanade and McRaeCKM17]
Theorem 10.8 [Reference CreutzigCre19]
Let ![]() $\mathfrak {g}$ be simply laced, and let
$\mathfrak {g}$ be simply laced, and let ![]() $\lambda \in Adm^{k}_{\mathbb {Z}}$,
$\lambda \in Adm^{k}_{\mathbb {Z}}$, ![]() $\mu \in Adm^{\check {k}}_{\mathbb {Z}}$. We have
$\mu \in Adm^{\check {k}}_{\mathbb {Z}}$. We have ![]() $\mathbf {L}^{k}_{[\lambda ,0]}\boxtimes \mathbf {L}^{k}_{[0,\mu ]}\cong \mathbf {L}^{k}_{[\lambda ,\mu ]}$. Moreover,
$\mathbf {L}^{k}_{[\lambda ,0]}\boxtimes \mathbf {L}^{k}_{[0,\mu ]}\cong \mathbf {L}^{k}_{[\lambda ,\mu ]}$. Moreover, ![]() $\mathbf {L}^{k}_{[\lambda ,0]}$ and
$\mathbf {L}^{k}_{[\lambda ,0]}$ and ![]() $\mathbf {L}^{\check {k}}_{[0,\mu ]}$ centralize each other if
$\mathbf {L}^{\check {k}}_{[0,\mu ]}$ centralize each other if ![]() $\lambda \in Adm^{k}_{\mathbb {Z}}\cap Q$.
$\lambda \in Adm^{k}_{\mathbb {Z}}\cap Q$.
Let f be admissible, and let f be an even nilpotent element in ![]() $\overline {\mathbb {O}_{k}}$. Then
$\overline {\mathbb {O}_{k}}$. Then ![]() $f\in \overline {\mathbb {O}_{k+1}}$ as well since
$f\in \overline {\mathbb {O}_{k+1}}$ as well since ![]() $\overline {\mathbb {O}_{k}}$ depends only on the denominator of k. Let
$\overline {\mathbb {O}_{k}}$ depends only on the denominator of k. Let ![]() $\ell $ be the number defined by
$\ell $ be the number defined by
that is,
Then ![]() $\ell $ is a nondegenerate admissible number. Note that
$\ell $ is a nondegenerate admissible number. Note that
where we have put ![]() $k+h^{\vee }=p/q$.
$k+h^{\vee }=p/q$.
Consider the ![]() $\mathscr {W}_{\ell }(\mathfrak {g})$-modules
$\mathscr {W}_{\ell }(\mathfrak {g})$-modules
Since the stabilizer of ![]() $0\in Adm^{\ell }_{\mathbb {Z}}$ of the
$0\in Adm^{\ell }_{\mathbb {Z}}$ of the ![]() $\tilde {W}_{+}$-action is trivial, the simple
$\tilde {W}_{+}$-action is trivial, the simple ![]() $\mathscr {W}_{\ell }(\mathfrak {g})$-modules
$\mathscr {W}_{\ell }(\mathfrak {g})$-modules ![]() $\mathbf {L}^{\ell }_{[0,\mu ]}$,
$\mathbf {L}^{\ell }_{[0,\mu ]}$, ![]() $\mu \in Adm_{\mathbb {Z}}^{\ell }$, are distinct. Therefore, by Theorem 10.4 (that is proved for
$\mu \in Adm_{\mathbb {Z}}^{\ell }$, are distinct. Therefore, by Theorem 10.4 (that is proved for ![]() $f=f_{prin}$ in [Reference CreutzigCre19]), the modules
$f=f_{prin}$ in [Reference CreutzigCre19]), the modules ![]() $\mathbf {L}^{\ell }_{[0,\mu ]}$,
$\mathbf {L}^{\ell }_{[0,\mu ]}$, ![]() $\mu \in Adm_{\mathbb {Z}}^{\ell }$ form a fusion full subcategory of
$\mu \in Adm_{\mathbb {Z}}^{\ell }$ form a fusion full subcategory of ![]() $\mathcal {C}^{ord}_{\mathscr {W}_{\ell }(\mathfrak {g})}$ that is equivalent to a category that can be called a simple current twist of
$\mathcal {C}^{ord}_{\mathscr {W}_{\ell }(\mathfrak {g})}$ that is equivalent to a category that can be called a simple current twist of ![]() $\mathcal {C}_{\mathbb {L}_{\check {\ell }}(\mathfrak {g})}^{ord}\cong \mathcal {C}_{\mathbb {L}_{k}(\mathfrak {g})}^{ord}$ (see [Reference CreutzigCre19, Thm.7.1] for the details). This simple current twist of
$\mathcal {C}_{\mathbb {L}_{\check {\ell }}(\mathfrak {g})}^{ord}\cong \mathcal {C}_{\mathbb {L}_{k}(\mathfrak {g})}^{ord}$ (see [Reference CreutzigCre19, Thm.7.1] for the details). This simple current twist of ![]() $\mathcal {C}_{\mathbb {L}_{k}(\mathfrak {g})}^{ord}$ is the fusion subcategory of
$\mathcal {C}_{\mathbb {L}_{k}(\mathfrak {g})}^{ord}$ is the fusion subcategory of ![]() $\mathcal {C}_{\mathbb {L}_{k}(\mathfrak {g})}^{ord} \boxtimes \mathcal {C}_{\mathbb {L}_{1}(\mathfrak {g})}^{ord}$ whose simple objects are the
$\mathcal {C}_{\mathbb {L}_{k}(\mathfrak {g})}^{ord} \boxtimes \mathcal {C}_{\mathbb {L}_{1}(\mathfrak {g})}^{ord}$ whose simple objects are the ![]() $\mathbb {L}^{k}_{\mu ,f}{\otimes } \mathbb {L}^{1}_{-\mu +Q}$. Call this category
$\mathbb {L}^{k}_{\mu ,f}{\otimes } \mathbb {L}^{1}_{-\mu +Q}$. Call this category ![]() $\mathcal {C}_{\mathbb {L}_{k}(\mathfrak {g})}^{ord, tw}$.
$\mathcal {C}_{\mathbb {L}_{k}(\mathfrak {g})}^{ord, tw}$.
Now set
By Theorem 8.6,
 $$ \begin{align} W \cong \bigoplus_{\substack{\lambda \in Adm^{k+1}_{\mathbb{Z}}\cap Q }} \mathbb{L}^{k+1}_{\lambda,f} \otimes \mathbf{L}^{\ell}_{[\lambda,0]}. \end{align} $$
$$ \begin{align} W \cong \bigoplus_{\substack{\lambda \in Adm^{k+1}_{\mathbb{Z}}\cap Q }} \mathbb{L}^{k+1}_{\lambda,f} \otimes \mathbf{L}^{\ell}_{[\lambda,0]}. \end{align} $$Hence, V is a vertex subalgebra of W. Moreover, each direct summand of W is an ordinary V-module and the sum is finite, and so W is an object of ![]() $\mathcal {C}_{V}^{ord}$.
$\mathcal {C}_{V}^{ord}$.
Clearly, the V-modules
form a monoidal full subcategory of ![]() $\mathcal {C}^{ord}_{V}$ that is equivalent to
$\mathcal {C}^{ord}_{V}$ that is equivalent to ![]() $ \mathcal {C}_{\mathbb {L}_{k}(\mathfrak {g})}^{ord}$. We denote by
$ \mathcal {C}_{\mathbb {L}_{k}(\mathfrak {g})}^{ord}$. We denote by ![]() $\mathcal {D}$ this fusion category.
$\mathcal {D}$ this fusion category.
By Theorem 10.8 and equation (63), we find that W centralizes any object of ![]() $\mathcal {D}$. Hence, we have the induction functor
$\mathcal {D}$. Hence, we have the induction functor
Theorem 10.9. The induction functor ![]() $\mathcal {F}: \mathcal {D}\rightarrow \mathcal {C}^{ord}_{W}$ is a fully faithful tensor functor that sends
$\mathcal {F}: \mathcal {D}\rightarrow \mathcal {C}^{ord}_{W}$ is a fully faithful tensor functor that sends ![]() $\mathbb {L}^{k+1}_{0,f}{\otimes } \mathbf {L}_{[0,\mu ]}^{\ell }$ to
$\mathbb {L}^{k+1}_{0,f}{\otimes } \mathbf {L}_{[0,\mu ]}^{\ell }$ to ![]() $\mathbb {L}^{k}_{\mu ,f}{\otimes } \mathbb {L}^{1}_{-\mu +Q}$, where
$\mathbb {L}^{k}_{\mu ,f}{\otimes } \mathbb {L}^{1}_{-\mu +Q}$, where ![]() $-\mu +Q$ denotes the class in
$-\mu +Q$ denotes the class in ![]() $ P/Q\cong P_{+}^{1}$.
$ P/Q\cong P_{+}^{1}$.
Proof. Thanks to [Reference CreutzigCre19, Theorem 3.5], it is sufficient to show that ![]() $\mathcal {F}(\mathbb {L}^{k+1}_{0,f}{\otimes } \mathbf {L}_{[0,\mu ]}^{\ell })$ is a simple W-module that is isomorphic to
$\mathcal {F}(\mathbb {L}^{k+1}_{0,f}{\otimes } \mathbf {L}_{[0,\mu ]}^{\ell })$ is a simple W-module that is isomorphic to ![]() $\mathbb {L}^{k}_{\mu ,f}{\otimes } \mathbb {L}^{1}_{-\mu +Q}$ for all
$\mathbb {L}^{k}_{\mu ,f}{\otimes } \mathbb {L}^{1}_{-\mu +Q}$ for all ![]() $\mu \in Adm^{\check {\ell }}_{\mathbb {Z}}$. As V-modules we have
$\mu \in Adm^{\check {\ell }}_{\mathbb {Z}}$. As V-modules we have
 $$ \begin{align*} \mathcal{F}(\mathbb{L}^{k+1}_{0,f}{\otimes} \mathbf{L}_{[0,\mu]}^{\ell}) = \bigoplus_{\substack{\lambda \in Adm^{k+1}_{\mathbb{Z}}\cap Q }} (\mathbb{L}^{k+1}_{\lambda,f} \otimes \mathbf{L}^{\ell}_{[\lambda,0]}) \boxtimes_{V} (\mathbb{L}^{k+1}_{0,f}{\otimes} \mathbf{L}_{[0,\mu]}^{\ell})\\ \cong \bigoplus_{\substack{\lambda \in Adm^{k+1}_{\mathbb{Z}}\cap Q }}\mathbb{L}^{k+1}_{\lambda,f} {\otimes} \mathbf{L}_{[\lambda,\mu]}^{\ell}\cong \mathbb{L}^{k}_{\mu,f}{\otimes} \mathbb{L}^{1}_{-\mu+Q} \end{align*} $$
$$ \begin{align*} \mathcal{F}(\mathbb{L}^{k+1}_{0,f}{\otimes} \mathbf{L}_{[0,\mu]}^{\ell}) = \bigoplus_{\substack{\lambda \in Adm^{k+1}_{\mathbb{Z}}\cap Q }} (\mathbb{L}^{k+1}_{\lambda,f} \otimes \mathbf{L}^{\ell}_{[\lambda,0]}) \boxtimes_{V} (\mathbb{L}^{k+1}_{0,f}{\otimes} \mathbf{L}_{[0,\mu]}^{\ell})\\ \cong \bigoplus_{\substack{\lambda \in Adm^{k+1}_{\mathbb{Z}}\cap Q }}\mathbb{L}^{k+1}_{\lambda,f} {\otimes} \mathbf{L}_{[\lambda,\mu]}^{\ell}\cong \mathbb{L}^{k}_{\mu,f}{\otimes} \mathbb{L}^{1}_{-\mu+Q} \end{align*} $$by Theorem 8.6 and Theorem 10.8. We claim this is indeed an isomorphism of W-modules. To see this, it is sufficient to show that there is a nontrivial W-module homomorphism ![]() $\mathcal {F}(\mathbb {L}^{k+1}_{0,f}{\otimes } \mathbf {L}_{[0,\mu ]}^{\ell }) \rightarrow \mathbb {L}^{k}_{\mu ,f}{\otimes } \mathbb {L}^{1}_{-\mu +Q}$ since
$\mathcal {F}(\mathbb {L}^{k+1}_{0,f}{\otimes } \mathbf {L}_{[0,\mu ]}^{\ell }) \rightarrow \mathbb {L}^{k}_{\mu ,f}{\otimes } \mathbb {L}^{1}_{-\mu +Q}$ since ![]() $\mathbb {L}^{k}_{\mu ,f}{\otimes } \mathbb {L}^{1}_{-\mu +Q}$ is simple. By the Frobenius reciprocity [Reference Kirillov and OstrikKO02, Reference Creutzig, Kanade and McRaeCKM17], we have
$\mathbb {L}^{k}_{\mu ,f}{\otimes } \mathbb {L}^{1}_{-\mu +Q}$ is simple. By the Frobenius reciprocity [Reference Kirillov and OstrikKO02, Reference Creutzig, Kanade and McRaeCKM17], we have
 $$ \begin{align*} &\operatorname{\mathrm{Hom}}_{W\operatorname{-Mod}}(\mathcal{F}(\mathbb{L}^{k+1}_{0,f}{\otimes} \mathbf{L}_{[0,\mu]}^{\ell}), \mathbb{L}^{k}_{\mu,f}{\otimes} \mathbb{L}^{1}_{-\mu+Q})\\ &\cong \operatorname{\mathrm{Hom}}_{V\operatorname{-Mod}}(\mathbb{L}^{k+1}_{0,f}{\otimes} \mathbf{L}_{[0,\mu]}^{\ell},\mathbb{L}^{k}_{\mu,f}{\otimes} \mathbb{L}^{1}_{-\mu+Q}) \\ &\cong \bigoplus_{\substack{\lambda \in Adm^{k+1}_{\mathbb{Z}}\cap Q }} \operatorname{\mathrm{Hom}}_{V\operatorname{-Mod}}(\mathbb{L}^{k+1}_{0,f}{\otimes} \mathbf{L}_{[0,\mu]}^{\ell},\mathbb{L}^{k+1}_{\lambda,f} {\otimes} \mathbf{L}_{[\lambda,\mu]}^{\ell}). \end{align*} $$
$$ \begin{align*} &\operatorname{\mathrm{Hom}}_{W\operatorname{-Mod}}(\mathcal{F}(\mathbb{L}^{k+1}_{0,f}{\otimes} \mathbf{L}_{[0,\mu]}^{\ell}), \mathbb{L}^{k}_{\mu,f}{\otimes} \mathbb{L}^{1}_{-\mu+Q})\\ &\cong \operatorname{\mathrm{Hom}}_{V\operatorname{-Mod}}(\mathbb{L}^{k+1}_{0,f}{\otimes} \mathbf{L}_{[0,\mu]}^{\ell},\mathbb{L}^{k}_{\mu,f}{\otimes} \mathbb{L}^{1}_{-\mu+Q}) \\ &\cong \bigoplus_{\substack{\lambda \in Adm^{k+1}_{\mathbb{Z}}\cap Q }} \operatorname{\mathrm{Hom}}_{V\operatorname{-Mod}}(\mathbb{L}^{k+1}_{0,f}{\otimes} \mathbf{L}_{[0,\mu]}^{\ell},\mathbb{L}^{k+1}_{\lambda,f} {\otimes} \mathbf{L}_{[\lambda,\mu]}^{\ell}). \end{align*} $$It follows that there is a nontrivial homomorphism corresponding to the identity map ![]() $\mathbb {L}^{k+1}_{0,f}{\otimes } \mathbf {L}_{[0,\mu ]}^{\ell }\rightarrow \mathbb {L}^{k+1}_{0,f}{\otimes } \mathbf {L}_{[0,\mu ]}^{\ell }$.
$\mathbb {L}^{k+1}_{0,f}{\otimes } \mathbf {L}_{[0,\mu ]}^{\ell }\rightarrow \mathbb {L}^{k+1}_{0,f}{\otimes } \mathbf {L}_{[0,\mu ]}^{\ell }$.
Proof of Theorem 10.4.
By Theorem 10.9, the correspondence
gives a tensor functor
where the last ![]() $\boxtimes $ denotes the Deligne product. This functor is fully faithful if and only if all the
$\boxtimes $ denotes the Deligne product. This functor is fully faithful if and only if all the ![]() $\mathbb {L}^{k}_{\mu ,f}$ are nonisomorphic. Since
$\mathbb {L}^{k}_{\mu ,f}$ are nonisomorphic. Since ![]() $\mathcal {C}_{\mathbb {L}_{1}(\mathfrak {g})}^{ord}$ is semisimple and its simple objects are all invertible, i.e., simple currents, this corresponds extends to a surjective tensor functor
$\mathcal {C}_{\mathbb {L}_{1}(\mathfrak {g})}^{ord}$ is semisimple and its simple objects are all invertible, i.e., simple currents, this corresponds extends to a surjective tensor functor
which restricts to a surjective tensor functor
that again is fully faithful if and only if all the ![]() $\mathbb {L}^{k}_{\mu ,f}$ are nonisomorphic.
$\mathbb {L}^{k}_{\mu ,f}$ are nonisomorphic.
Let us conclude with a remark on the general case.
Remark 10.10. It is a well-known result of Kazhdan–Lusztig that ordinary modules of affine vertex algebras at generic level have vertex tensor category [Reference Kazhdan and LusztigKL1, Reference Kazhdan and LusztigKL2, Reference Kazhdan and LusztigKL3, Reference Kazhdan and LusztigKL4], and it is reasonable to expect that a similar result might hold for ![]() $\mathscr {W}$-algebras as well. However, this is only proven for the Virasoro algebra [Reference Creutzig, Jiang, Hunziker, Ridout and YangCJORY20] and the
$\mathscr {W}$-algebras as well. However, this is only proven for the Virasoro algebra [Reference Creutzig, Jiang, Hunziker, Ridout and YangCJORY20] and the ![]() $N=1$ super Virasoro algebra [Reference Creutzig, McRae and YangCMY20].
$N=1$ super Virasoro algebra [Reference Creutzig, McRae and YangCMY20].
At generic levels one has to deal with infinite order extensions of vertex algebras, and so one needs to consider completions of vertex tensor categories. The theory of vertex algebra extension also works for such completions [Reference Creutzig, McRae and YangCMY20]. This means that if one can prove the existence of vertex tensor category structure on categories of ordinary modules of ![]() $\mathscr {W}$-algebras at generic levels, then one can also derive results for generic levels that are similar to the statements of this section.
$\mathscr {W}$-algebras at generic levels, then one can also derive results for generic levels that are similar to the statements of this section.
Acknowledgements
T.A. is partially supported by JSPS KAKENHI Grant Numbers 17H01086, 17K18724, 19K21828, 21H04993. The study of B.F. has been funded within the framework of the HSE University Basic Research Program and the Russian Academic Excellence Project ‘5-100’. T.C. appreciates discussions with Sergei Gukov and Emanuel Diaconescu. T.C. is supported by NSERC ![]() $\#$RES0048511.
$\#$RES0048511.
Conflict of Interest
None.