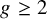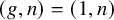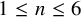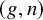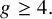1 Introduction
The moduli stack
![]() $\overline {\mathcal {M}}_{g}$
of stable genus
$\overline {\mathcal {M}}_{g}$
of stable genus
![]() $g \geq 2$
curves as introduced by Deligne-Mumford [Reference Deligne and MumfordDM69] has the beautiful property that it is a proper and smooth Deligne-Mumford stack over
$g \geq 2$
curves as introduced by Deligne-Mumford [Reference Deligne and MumfordDM69] has the beautiful property that it is a proper and smooth Deligne-Mumford stack over
![]() $\operatorname {\mathrm {Spec}}(\mathbb Z)$
. When it comes to schemes, the few known examples that share this property are typically rational and therefore do not carry nontrivial Brauer classes. It is then natural to ask whether
$\operatorname {\mathrm {Spec}}(\mathbb Z)$
. When it comes to schemes, the few known examples that share this property are typically rational and therefore do not carry nontrivial Brauer classes. It is then natural to ask whether
![]() $\overline {\mathcal {M}}_{g}$
carries nontrivial Brauer classes defined over
$\overline {\mathcal {M}}_{g}$
carries nontrivial Brauer classes defined over
![]() $\mathbb Z$
or an algebraic closure
$\mathbb Z$
or an algebraic closure
![]() $\overline {\mathbb Q}$
of
$\overline {\mathbb Q}$
of
![]() $\mathbb Q$
. The main result of this note claims that this is not the case; more precisely, we show the following:
$\mathbb Q$
. The main result of this note claims that this is not the case; more precisely, we show the following:
Theorem 1.1 (see Corollary 3.8 and Section 4).
The equalities
hold for all
![]() $g\geq 2$
. For integers
$g\geq 2$
. For integers
![]() $g, n \geq 0$
such that
$g, n \geq 0$
such that
![]() $2g-2+n>0$
, the equalities
$2g-2+n>0$
, the equalities
hold for
![]() $(g, n)=(1,n)$
with
$(g, n)=(1,n)$
with
![]() $1\leq n \leq 6$
and for all
$1\leq n \leq 6$
and for all
![]() $(g,n)$
with
$(g,n)$
with
![]() $g=0$
or
$g=0$
or
![]() $g\geq 4.$
$g\geq 4.$
Here,
![]() $\overline {\mathcal {M}}_{g, n}$
stands for the moduli stack of stable genus g curves with n marked points, which is also a proper and smooth Deligne-Mumford stack; see Section 1.3. In the following discussion, we also need the moduli stack
$\overline {\mathcal {M}}_{g, n}$
stands for the moduli stack of stable genus g curves with n marked points, which is also a proper and smooth Deligne-Mumford stack; see Section 1.3. In the following discussion, we also need the moduli stack
![]() $\mathcal {M}_{g, n} \subset \overline {\mathcal {M}}_{g, n}$
of smooth genus g curves with n marked points.
$\mathcal {M}_{g, n} \subset \overline {\mathcal {M}}_{g, n}$
of smooth genus g curves with n marked points.
Remark 1.2. By our convention to denote by
![]() $\operatorname {\mathrm {Br}}(-)$
the cohomological Brauer group and since the Deligne-Mumford stacks
$\operatorname {\mathrm {Br}}(-)$
the cohomological Brauer group and since the Deligne-Mumford stacks
![]() $\overline {\mathcal {M}}_{g,n,\mathbb Z}$
and
$\overline {\mathcal {M}}_{g,n,\mathbb Z}$
and
![]() $\overline {\mathcal {M}}_{g,n,\overline {\mathbb {Q}}}$
are regular, our result means that
$\overline {\mathcal {M}}_{g,n,\overline {\mathbb {Q}}}$
are regular, our result means that
in the above range of
![]() $(g,n).$
$(g,n).$
Remark 1.3. The equalities
![]() $ \operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{0,n,\mathbb Z})=\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{0,n,\overline {\mathbb {Q}}})=0 $
for all
$ \operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{0,n,\mathbb Z})=\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{0,n,\overline {\mathbb {Q}}})=0 $
for all
![]() $n \geq 3$
are well known. For this, we first note that
$n \geq 3$
are well known. For this, we first note that
![]() $\overline {\mathcal {M}}_{0,n,\mathbb Z}$
is a scheme. The desired equalities follow (cf., the proof of [Reference PoonenPoo17, Lemma 6.9.8]) from the fact that
$\overline {\mathcal {M}}_{0,n,\mathbb Z}$
is a scheme. The desired equalities follow (cf., the proof of [Reference PoonenPoo17, Lemma 6.9.8]) from the fact that
![]() $\overline {\mathcal {M}}_{0,n,\mathbb {Q}}$
is a rational proper smooth scheme over
$\overline {\mathcal {M}}_{0,n,\mathbb {Q}}$
is a rational proper smooth scheme over
![]() $\mathbb {Q}$
and
$\mathbb {Q}$
and
![]() $\overline {\mathcal {M}}_{0,n, \mathbb Z}$
has a
$\overline {\mathcal {M}}_{0,n, \mathbb Z}$
has a
![]() $\mathbb Z$
-section.
$\mathbb Z$
-section.
Remark 1.4. Assume that
![]() $g \geq 1$
. To the best of our knowledge, vanishing of
$g \geq 1$
. To the best of our knowledge, vanishing of
![]() $\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{g,n,\overline {\mathbb {Q}}})$
was known in the following cases of
$\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{g,n,\overline {\mathbb {Q}}})$
was known in the following cases of
![]() $(g,n)$
:
$(g,n)$
:
-
(1,1): Antieau-Meier [Reference Antieau and MeierAM20] show the stronger statement
 $\operatorname {\mathrm {Br}}(\mathcal {M}_{1,1,\overline {\mathbb {Q}}})=0$
. (In Proposition 4.1, we give an independent argument. We stress that this vanishing is an easy part of [Reference Antieau and MeierAM20].)
$\operatorname {\mathrm {Br}}(\mathcal {M}_{1,1,\overline {\mathbb {Q}}})=0$
. (In Proposition 4.1, we give an independent argument. We stress that this vanishing is an easy part of [Reference Antieau and MeierAM20].) -
(1,2): It follows from a result of Inchiostro [Reference InchiostroInc22, Theorem 1.2] that
 $\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{1,2, \overline {\mathbb Q}})=0$
(see also Proposition 4.2).
$\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{1,2, \overline {\mathbb Q}})=0$
(see also Proposition 4.2). -
(2,0): Here, the result follows from [Reference Di Lorenzo and PirisiDLP21]; see Proposition 4.3.
-
g ≥ 4: Here, the result follows from [Reference Korkmaz and StipsiczKS03]; see Theorem 4.15.
Therefore, the new cases established in this paper are the case
![]() $(g, n)=(3, 0)$
and the case
$(g, n)=(3, 0)$
and the case
![]() $(g, n)=(1,n)$
with
$(g, n)=(1,n)$
with
![]() $3\leq n \leq 6$
.
$3\leq n \leq 6$
.
When it comes to vanishing of
![]() $\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{g,n,\mathbb Z})$
, the only known statement that we are aware of concerns the case
$\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{g,n,\mathbb Z})$
, the only known statement that we are aware of concerns the case
![]() $(g, n)=(1,1).$
Namely, in the aforementioned article of Antieau-Meier [Reference Antieau and MeierAM20], they show as their main result that
$(g, n)=(1,1).$
Namely, in the aforementioned article of Antieau-Meier [Reference Antieau and MeierAM20], they show as their main result that
which implies
![]() $\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{1,1,\mathbb Z})=0$
(yet again, our argument for
$\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{1,1,\mathbb Z})=0$
(yet again, our argument for
![]() $\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{1,1,\mathbb Z})=0$
is independent of their work).
$\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{1,1,\mathbb Z})=0$
is independent of their work).
Remark 1.5. Since we have
(see Lemma 2.7), our result shows that
![]() $H^3_{\operatorname {\acute {e}t}}(\overline {\mathcal {M}}_{g,n,\overline {\mathbb {Q}}}, \mathbb Z_\ell (1))_{\mathrm {tor}}=0$
for any prime
$H^3_{\operatorname {\acute {e}t}}(\overline {\mathcal {M}}_{g,n,\overline {\mathbb {Q}}}, \mathbb Z_\ell (1))_{\mathrm {tor}}=0$
for any prime
![]() $\ell $
in the range of
$\ell $
in the range of
![]() $(g,n)$
stated in Theorem 1.1. In fact, together with an extension of a classical result due to Abrashkin and Fontaine ([Reference AbrashkinAbr90], [Reference FontaineFon93]) to Deligne-Mumford stacks that are proper and smooth over
$(g,n)$
stated in Theorem 1.1. In fact, together with an extension of a classical result due to Abrashkin and Fontaine ([Reference AbrashkinAbr90], [Reference FontaineFon93]) to Deligne-Mumford stacks that are proper and smooth over
![]() $\operatorname {\mathrm {Spec}}(\mathbb Z)$
(see Theorem 2.8), this implies that
$\operatorname {\mathrm {Spec}}(\mathbb Z)$
(see Theorem 2.8), this implies that
![]() $H^3_{\operatorname {\acute {e}t}}(\overline {\mathcal {M}}_{g,n,\overline {\mathbb {Q}}}, \mathbb Z_\ell (1))=0$
for any prime
$H^3_{\operatorname {\acute {e}t}}(\overline {\mathcal {M}}_{g,n,\overline {\mathbb {Q}}}, \mathbb Z_\ell (1))=0$
for any prime
![]() $\ell $
. It would be interesting to investigate whether our main result also extends to the missing cases (namely,
$\ell $
. It would be interesting to investigate whether our main result also extends to the missing cases (namely,
![]() $(1,n)$
with
$(1,n)$
with
![]() $n\geq 7$
and
$n\geq 7$
and
![]() $(2,n),(3,n)$
with
$(2,n),(3,n)$
with
![]() $n\geq 1$
), but we currently do not know how to approach these cases. Let us also mention here that it is, however, not true in general that
$n\geq 1$
), but we currently do not know how to approach these cases. Let us also mention here that it is, however, not true in general that
![]() $ H^{3}(\overline {\mathcal {M}}_{g,n,\overline {\mathbb {Q}}},\mathbb {Z}/2\mathbb {Z})=0 $
(even for
$ H^{3}(\overline {\mathcal {M}}_{g,n,\overline {\mathbb {Q}}},\mathbb {Z}/2\mathbb {Z})=0 $
(even for
![]() $g \geq 4$
). This follows from [Reference Ebert and GiansiracusaEG11, Theorem 1.2], but we omit the details here.
$g \geq 4$
). This follows from [Reference Ebert and GiansiracusaEG11, Theorem 1.2], but we omit the details here.
We are not aware of an example of a proper and smooth scheme X over
![]() $\operatorname {\mathrm {Spec}} (\mathbb Z)$
with non-trivial
$\operatorname {\mathrm {Spec}} (\mathbb Z)$
with non-trivial
![]() $\operatorname {\mathrm {Br}}(X)$
or
$\operatorname {\mathrm {Br}}(X)$
or
![]() $\operatorname {\mathrm {Br}}(X_{\overline {\mathbb {Q}}})$
and, as the result of Abrashkin and Fontaine ([Reference AbrashkinAbr90], [Reference FontaineFon93]) indicates, it seems that there are not ‘many’ examples of proper and smooth schemes over
$\operatorname {\mathrm {Br}}(X_{\overline {\mathbb {Q}}})$
and, as the result of Abrashkin and Fontaine ([Reference AbrashkinAbr90], [Reference FontaineFon93]) indicates, it seems that there are not ‘many’ examples of proper and smooth schemes over
![]() $\operatorname {\mathrm {Spec}} (\mathbb Z)$
. However, we have a lot of interesting examples of proper and smooth Deligne-Mumford stacks over
$\operatorname {\mathrm {Spec}} (\mathbb Z)$
. However, we have a lot of interesting examples of proper and smooth Deligne-Mumford stacks over
![]() $\operatorname {\mathrm {Spec}} (\mathbb Z)$
, such as
$\operatorname {\mathrm {Spec}} (\mathbb Z)$
, such as
![]() $\overline {\mathcal {M}}_{g,n,\mathbb Z}$
. We remark that there are quite easy examples of Deligne-Mumford stacks X that are proper and smooth over
$\overline {\mathcal {M}}_{g,n,\mathbb Z}$
. We remark that there are quite easy examples of Deligne-Mumford stacks X that are proper and smooth over
![]() $\operatorname {\mathrm {Spec}} (\mathbb Z)$
, such that
$\operatorname {\mathrm {Spec}} (\mathbb Z)$
, such that
![]() $\operatorname {\mathrm {Br}}(X)$
does not vanish respectively such that
$\operatorname {\mathrm {Br}}(X)$
does not vanish respectively such that
![]() $\operatorname {\mathrm {Br}}(X_{\overline {\mathbb {Q}}})$
does not vanish (see Examples 3.13 and 3.14). In other words, the vanishing patterns proven in this article are not general features of proper and smooth Deligne-Mumford stacks over
$\operatorname {\mathrm {Br}}(X_{\overline {\mathbb {Q}}})$
does not vanish (see Examples 3.13 and 3.14). In other words, the vanishing patterns proven in this article are not general features of proper and smooth Deligne-Mumford stacks over
![]() $\operatorname {\mathrm {Spec}} (\mathbb Z)$
; they might be specific to the stack
$\operatorname {\mathrm {Spec}} (\mathbb Z)$
; they might be specific to the stack
![]() $\overline {\mathcal {M}}_{g,n}$
(and maybe to schemes).
$\overline {\mathcal {M}}_{g,n}$
(and maybe to schemes).
Remark 1.6. Along the way, we will prove that for Deligne-Mumford stacks X that are proper and smooth over
![]() $\operatorname {\mathrm {Spec}} (\mathbb Z)$
, the Brauer group
$\operatorname {\mathrm {Spec}} (\mathbb Z)$
, the Brauer group
![]() $\operatorname {\mathrm {Br}}(X)$
is finite; see Theorem 3.4. This may fit into the following conjecture of Artin ([Reference GrothendieckGro68, Remarque 2.5 (c)]): the Brauer group of every proper scheme over
$\operatorname {\mathrm {Br}}(X)$
is finite; see Theorem 3.4. This may fit into the following conjecture of Artin ([Reference GrothendieckGro68, Remarque 2.5 (c)]): the Brauer group of every proper scheme over
![]() $\operatorname {\mathrm {Spec}} (\mathbb Z)$
is finite. However, the conjecture of Artin is widely open and is in general much more difficult than the case we are considering here.
$\operatorname {\mathrm {Spec}} (\mathbb Z)$
is finite. However, the conjecture of Artin is widely open and is in general much more difficult than the case we are considering here.
1.1 Outline of the proof
Our argument for proving Theorem 1.1 proceeds by establishing vanishing of the Brauer group of
![]() $\overline {\mathcal {M}}_{g,n,\overline {\mathbb {Q}}}$
and then deducing vanishing over the integers; see Section 3.2 for this reduction step, which may be interesting in its own right.
$\overline {\mathcal {M}}_{g,n,\overline {\mathbb {Q}}}$
and then deducing vanishing over the integers; see Section 3.2 for this reduction step, which may be interesting in its own right.
As explained in Remark 1.4 (and Remark 1.3), our results over
![]() $\overline {\mathbb {Q}}$
are new for
$\overline {\mathbb {Q}}$
are new for
![]() $(g, n)=(3, 0)$
and for
$(g, n)=(3, 0)$
and for
![]() $(g, n)=(1,n)$
with
$(g, n)=(1,n)$
with
![]() $3\leq n \leq 6$
. Here, we outline the proofs for these new cases (but we also give independent arguments for some previous results in the main body of the paper).
$3\leq n \leq 6$
. Here, we outline the proofs for these new cases (but we also give independent arguments for some previous results in the main body of the paper).
Our argument for the case
![]() $(g, n)=(3, 0)$
goes as follows: By the work of Di Lorenzo-Pirisi [Reference Lorenzo and PirisiLP24], one knows that for any field k with
$(g, n)=(3, 0)$
goes as follows: By the work of Di Lorenzo-Pirisi [Reference Lorenzo and PirisiLP24], one knows that for any field k with
![]() $p=\text {char}(k)\neq 2,$
$p=\text {char}(k)\neq 2,$
where
![]() $B_{p}=0$
if
$B_{p}=0$
if
![]() $\text {char}(k)=0$
and a p-primary torsion group otherwise. We first reduce the problem of showing that
$\text {char}(k)=0$
and a p-primary torsion group otherwise. We first reduce the problem of showing that
![]() $\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{3, \overline {\mathbb {Q}}})=0$
to showing that
$\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{3, \overline {\mathbb {Q}}})=0$
to showing that
![]() $\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{3, \overline {\mathbb {F}}_{p}})[2]=0$
for some prime
$\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{3, \overline {\mathbb {F}}_{p}})[2]=0$
for some prime
![]() $p\neq 2.$
Our task is therefore to show that the generator
$p\neq 2.$
Our task is therefore to show that the generator
![]() $\gamma $
of the factor
$\gamma $
of the factor
![]() $\mathbb Z/2\mathbb Z$
in
$\mathbb Z/2\mathbb Z$
in
![]() $\operatorname {\mathrm {Br}}(\mathcal {M}_{3,\mathbb {F}_{q}})[2]$
does not extend to the compactification for a finite field
$\operatorname {\mathrm {Br}}(\mathcal {M}_{3,\mathbb {F}_{q}})[2]$
does not extend to the compactification for a finite field
![]() $\mathbb {F}_{q}$
of characteristic p. Using that
$\mathbb {F}_{q}$
of characteristic p. Using that
![]() $\operatorname {\mathrm {Br}}(\mathbb {F}_{q}[[t]])=0,$
it is easy to see that it suffices for this to produce a stable curve of genus three
$\operatorname {\mathrm {Br}}(\mathbb {F}_{q}[[t]])=0,$
it is easy to see that it suffices for this to produce a stable curve of genus three
![]() $\mathscr {C}$
over
$\mathscr {C}$
over
![]() $\mathbb {F}_{q}[[t]],$
such that the generic fiber
$\mathbb {F}_{q}[[t]],$
such that the generic fiber
![]() $C=\mathscr {C}_{\eta }$
is a smooth genus three curve over
$C=\mathscr {C}_{\eta }$
is a smooth genus three curve over
![]() $F=\mathbb {F}_{q}((t))$
, which has the property that
$F=\mathbb {F}_{q}((t))$
, which has the property that
![]() $\gamma (C) \in \operatorname {\mathrm {Br}}(F)[2]$
is nontrivial. To achieve this, we use the beautiful relation found by Di Lorenzo-Pirisi between the factor
$\gamma (C) \in \operatorname {\mathrm {Br}}(F)[2]$
is nontrivial. To achieve this, we use the beautiful relation found by Di Lorenzo-Pirisi between the factor
![]() $\gamma $
and the étale algebra of 27 lines on smooth cubic surfaces X obtained by blowing up (general) six points in
$\gamma $
and the étale algebra of 27 lines on smooth cubic surfaces X obtained by blowing up (general) six points in
![]() $\mathbb {P}^{2}$
, and the result of Shioda [Reference ShiodaShi95] on very explicit defining equations of smooth quartic curves which arise as the ramification locus of some projection
$\mathbb {P}^{2}$
, and the result of Shioda [Reference ShiodaShi95] on very explicit defining equations of smooth quartic curves which arise as the ramification locus of some projection
![]() $X \dashrightarrow \mathbb {P}^{2}$
. The upshot is that for
$X \dashrightarrow \mathbb {P}^{2}$
. The upshot is that for
![]() $p\geq 11$
, we are able to find such curves; see Section 4.3 for details.
$p\geq 11$
, we are able to find such curves; see Section 4.3 for details.
For the cases
![]() $(1,n)$
with
$(1,n)$
with
![]() $3\leq n \leq 6$
(also for
$3\leq n \leq 6$
(also for
![]() $n=1, 2$
), we give a uniform argument; see Proposition 4.2. Namely, we use recent work of Battistella-Di Lorenzo [Reference Battistella and LorenzoBL24] (relying on work of Smyth [Reference SmythSmy19] and Lekili-Polishchuk [Reference Lekili and PolishchukLP19]), who explain that in these cases, the stack
$n=1, 2$
), we give a uniform argument; see Proposition 4.2. Namely, we use recent work of Battistella-Di Lorenzo [Reference Battistella and LorenzoBL24] (relying on work of Smyth [Reference SmythSmy19] and Lekili-Polishchuk [Reference Lekili and PolishchukLP19]), who explain that in these cases, the stack
![]() $\overline {\mathcal {M}}_{1,n}$
is connected to a stacky weighted projective space (resp. Grassmannian) by a diagram of smooth Deligne-Mumford stacks along weighted (and ordinary) blow-ups. Vanishing of the Brauer group of a stacky weighted projective space over
$\overline {\mathcal {M}}_{1,n}$
is connected to a stacky weighted projective space (resp. Grassmannian) by a diagram of smooth Deligne-Mumford stacks along weighted (and ordinary) blow-ups. Vanishing of the Brauer group of a stacky weighted projective space over
![]() $\overline {\mathbb {Q}}$
follows from the work of Shin [Reference ShinShi23], and we deduce the desired result by using purity of the Brauer group (see Proposition 2.2) as established by Česnavičius [Reference ČesnavičiusČes19].
$\overline {\mathbb {Q}}$
follows from the work of Shin [Reference ShinShi23], and we deduce the desired result by using purity of the Brauer group (see Proposition 2.2) as established by Česnavičius [Reference ČesnavičiusČes19].
1.2 Structure of the article
In Section 2, we collect some results which are extensions of well-known results in the context of schemes to the setting of Deligne-Mumford stacks, which will be used later. In Section 3, we first show finiteness of the Brauer group of a proper and smooth Deligne-Mumford stack X over
![]() $\operatorname {\mathrm {Spec}}(\mathbb Z)$
(see Theorem 3.4), and then we explain how in this setting, it is often possible (in particular, possible for
$\operatorname {\mathrm {Spec}}(\mathbb Z)$
(see Theorem 3.4), and then we explain how in this setting, it is often possible (in particular, possible for
![]() $X=\overline {\mathcal {M}}_{g,n}$
) to reduce vanishing of
$X=\overline {\mathcal {M}}_{g,n}$
) to reduce vanishing of
![]() $\operatorname {\mathrm {Br}}(X)$
to vanishing of
$\operatorname {\mathrm {Br}}(X)$
to vanishing of
![]() $\operatorname {\mathrm {Br}}(X_{\overline {\mathbb {Q}}})$
; see Proposition 3.5. We end that section with a discussion of some examples. Finally, in Section 4, we prove our vanishing results on
$\operatorname {\mathrm {Br}}(X_{\overline {\mathbb {Q}}})$
; see Proposition 3.5. We end that section with a discussion of some examples. Finally, in Section 4, we prove our vanishing results on
![]() $\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{g,n, \overline {\mathbb {Q}}})$
.
$\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{g,n, \overline {\mathbb {Q}}})$
.
1.3 Conventions, notations and recollections
All Deligne-Mumford (DM) stacks considered in this paper will be assumed to be quasi-separated. If X is a scheme or DM stack, we denote by
the cohomological Brauer group. Here, for an abelian group M, we let
![]() $M_{\operatorname {\mathrm {tors}}}$
denote its torsion part. Recall that
$M_{\operatorname {\mathrm {tors}}}$
denote its torsion part. Recall that
![]() $\operatorname {\mathrm {Br}}(X)=H^{2}_{\operatorname {\acute {e}t}}(X,\mathbb {G}_{m})$
if X is noetherian and regular (see [Reference Antieau and MeierAM20, Proposition 2.5]). Recall here that a DM stack X is called regular if there exists an étale presentation of X by a regular scheme (then all presentations will be by regular schemes). We use the notion of the codimension of a closed substack of a noetherian DM stack as in [Reference OssermanOss13, Definition 6.1].
$\operatorname {\mathrm {Br}}(X)=H^{2}_{\operatorname {\acute {e}t}}(X,\mathbb {G}_{m})$
if X is noetherian and regular (see [Reference Antieau and MeierAM20, Proposition 2.5]). Recall here that a DM stack X is called regular if there exists an étale presentation of X by a regular scheme (then all presentations will be by regular schemes). We use the notion of the codimension of a closed substack of a noetherian DM stack as in [Reference OssermanOss13, Definition 6.1].
For integers
![]() $g, n \geq 0$
such that
$g, n \geq 0$
such that
![]() $2g-2+n>0$
, we denote by
$2g-2+n>0$
, we denote by
![]() $\mathcal {M}_{g,n}$
the moduli stack of smooth genus g curves with n marked points, and by
$\mathcal {M}_{g,n}$
the moduli stack of smooth genus g curves with n marked points, and by
![]() $\overline {\mathcal {M}}_{g,n}$
the moduli stack of stable genus g curves with n marked points; see [Reference KnudsenKnu83, Section 1] for example for the basic definition. If
$\overline {\mathcal {M}}_{g,n}$
the moduli stack of stable genus g curves with n marked points; see [Reference KnudsenKnu83, Section 1] for example for the basic definition. If
![]() $n=0$
(so that
$n=0$
(so that
![]() $g \geq 2$
), then we write
$g \geq 2$
), then we write
![]() $\mathcal {M}_{g}:=\mathcal {M}_{g,0}$
and
$\mathcal {M}_{g}:=\mathcal {M}_{g,0}$
and
![]() $\overline {\mathcal {M}}_{g}:=\overline {\mathcal {M}}_{g,0}$
. It is well known that
$\overline {\mathcal {M}}_{g}:=\overline {\mathcal {M}}_{g,0}$
. It is well known that
![]() $\overline {\mathcal {M}}_{g,n}$
is a proper and smooth DM stack over
$\overline {\mathcal {M}}_{g,n}$
is a proper and smooth DM stack over
![]() $\operatorname {\mathrm {Spec}} (\mathbb Z)$
with geometric connected fibers and
$\operatorname {\mathrm {Spec}} (\mathbb Z)$
with geometric connected fibers and
![]() $\mathcal {M}_{g,n} \subset \overline {\mathcal {M}}_{g,n}$
is open and dense. See [Reference Deligne and MumfordDM69] and [Reference KnudsenKnu83]. For a ring R, we denote by
$\mathcal {M}_{g,n} \subset \overline {\mathcal {M}}_{g,n}$
is open and dense. See [Reference Deligne and MumfordDM69] and [Reference KnudsenKnu83]. For a ring R, we denote by
![]() $\mathcal {M}_{g,n, R}$
and
$\mathcal {M}_{g,n, R}$
and
![]() $\overline {\mathcal {M}}_{g,n, R}$
the base changes to
$\overline {\mathcal {M}}_{g,n, R}$
the base changes to
![]() $\operatorname {\mathrm {Spec}} (R)$
. We implicitly always assume that
$\operatorname {\mathrm {Spec}} (R)$
. We implicitly always assume that
![]() $2g-2+n>0$
when considering these moduli stacks.
$2g-2+n>0$
when considering these moduli stacks.
2 Preparations
We start by collecting some statements we need for our arguments later.
Lemma 2.1. Let k be a field, X a smooth DM stack over
![]() $\operatorname {\mathrm {Spec}}(k),$
and
$\operatorname {\mathrm {Spec}}(k),$
and
![]() $Z\hookrightarrow X$
a closed DM substack, which is also smooth over
$Z\hookrightarrow X$
a closed DM substack, which is also smooth over
![]() $\operatorname {\mathrm {Spec}}(k).$
Consider the blow-up
$\operatorname {\mathrm {Spec}}(k).$
Consider the blow-up
![]() $\operatorname {\mathrm {Bl}}_{Z}(X)$
of X along Z (see, for example, [Reference Quek and RydhQD22, Example 3.2.6] for a definition). Then
$\operatorname {\mathrm {Bl}}_{Z}(X)$
of X along Z (see, for example, [Reference Quek and RydhQD22, Example 3.2.6] for a definition). Then
![]() $\operatorname {\mathrm {Bl}}_{Z}(X)$
is smooth over
$\operatorname {\mathrm {Bl}}_{Z}(X)$
is smooth over
![]() $\operatorname {\mathrm {Spec}}(k).$
$\operatorname {\mathrm {Spec}}(k).$
Proof. Let
![]() $U\rightarrow X$
be an étale presentation of X by a scheme
$U\rightarrow X$
be an étale presentation of X by a scheme
![]() $U.$
Since blowing up commutes with flat localization on the base ([Reference Quek and RydhQD22, Corollary 3.2.14 (iii)]), we obtain the étale presentation
$U.$
Since blowing up commutes with flat localization on the base ([Reference Quek and RydhQD22, Corollary 3.2.14 (iii)]), we obtain the étale presentation
and it suffices by the definition of a smooth morphism of algebraic stacks ([Sta22, Tag 075U]) to show that
![]() $\operatorname {\mathrm {Bl}}_{Z_{U}}(U)$
is a smooth scheme over
$\operatorname {\mathrm {Bl}}_{Z_{U}}(U)$
is a smooth scheme over
![]() $\operatorname {\mathrm {Spec}}(k).$
But then
$\operatorname {\mathrm {Spec}}(k).$
But then
![]() $Z_{U}$
is Zariski locally cut out in U by a regular sequence, and the result is classical.
$Z_{U}$
is Zariski locally cut out in U by a regular sequence, and the result is classical.
We next deduce the following purity statement for the Brauer group of a noetherian and regular DM stack from results of Česnavičius [Reference ČesnavičiusČes19]; this is stronger than what we will later need, but we wanted to record it here.
Proposition 2.2. Let X be a noetherian and regular DM stack and
![]() $Z\hookrightarrow X$
a closed substack such that
$Z\hookrightarrow X$
a closed substack such that
![]() $\operatorname {\mathrm {codim}}_{X}(Z)\geq 2.$
Then the natural restriction map
$\operatorname {\mathrm {codim}}_{X}(Z)\geq 2.$
Then the natural restriction map
is an isomorphism for
![]() $i \leq 2$
and is injective for
$i \leq 2$
and is injective for
![]() $i=3$
.
$i=3$
.
Proof. As explained in the proof of [Reference ČesnavičiusČes19, Theorem 6.1], we can work étale locally and reduce the desired statement to the case where X is a scheme (or more precisely, the spectrum of a strictly henselian regular local ring), and thus, this proposition follows from the result proved there.
Corollary 2.3. Let
![]() $\pi \colon \widetilde {X}\rightarrow X$
be a morphism of noetherian and regular DM stacks which is an isomorphism on a dense open substack
$\pi \colon \widetilde {X}\rightarrow X$
be a morphism of noetherian and regular DM stacks which is an isomorphism on a dense open substack
![]() $U\subset X.$
$U\subset X.$
-
1. The homomorphism
 $\pi ^{*} \colon \operatorname {\mathrm {Br}}(X)\rightarrow \operatorname {\mathrm {Br}}(\widetilde {X})$
is injective.
$\pi ^{*} \colon \operatorname {\mathrm {Br}}(X)\rightarrow \operatorname {\mathrm {Br}}(\widetilde {X})$
is injective. -
2. If the complement Z of U in X satisfies
 $\operatorname {\mathrm {codim}}_{X}(Z)\geq 2,$
then if
$\operatorname {\mathrm {codim}}_{X}(Z)\geq 2,$
then if
 $\operatorname {\mathrm {Br}}(X)=0,$
also
$\operatorname {\mathrm {Br}}(X)=0,$
also
 $\operatorname {\mathrm {Br}}(\widetilde {X})=0.$
$\operatorname {\mathrm {Br}}(\widetilde {X})=0.$
Proof. The first part follows because both
![]() $\operatorname {\mathrm {Br}}(X)$
and
$\operatorname {\mathrm {Br}}(X)$
and
![]() $\operatorname {\mathrm {Br}}(\widetilde {X})$
embed into
$\operatorname {\mathrm {Br}}(\widetilde {X})$
embed into
![]() $\operatorname {\mathrm {Br}}(U)$
([Reference Antieau and MeierAM20, Proposition 2.5 (iv)]). For the second part, purity of the Brauer group (Proposition 2.2) implies that
$\operatorname {\mathrm {Br}}(U)$
([Reference Antieau and MeierAM20, Proposition 2.5 (iv)]). For the second part, purity of the Brauer group (Proposition 2.2) implies that
![]() $\operatorname {\mathrm {Br}}(U)=0,$
so that by [Reference Antieau and MeierAM20, Proposition 2.5 (iv)] again, we see that
$\operatorname {\mathrm {Br}}(U)=0,$
so that by [Reference Antieau and MeierAM20, Proposition 2.5 (iv)] again, we see that
![]() $\operatorname {\mathrm {Br}}(\widetilde {X})=0,$
as desired.
$\operatorname {\mathrm {Br}}(\widetilde {X})=0,$
as desired.
Next, we want to record some extensions to the setting of DM stacks of statements in étale cohomology which are classical for schemes; these results are most probably well known to the experts.
Lemma 2.4. Let
![]() $X\rightarrow \operatorname {\mathrm {Spec}}(\mathbb Z)$
be a proper and smooth DM stack. The
$X\rightarrow \operatorname {\mathrm {Spec}}(\mathbb Z)$
be a proper and smooth DM stack. The
![]() $\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$
-representation
$\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$
-representation
is unramified at
![]() $\ell \neq p$
and crystalline at
$\ell \neq p$
and crystalline at
![]() $p.$
$p.$
Proof. The claim about unramifiedness at
![]() $\ell \neq p$
follows from [Reference van den Bogaart and EdixhovenvdBE05, Proposition 3.1] and about being crystalline at p from [Reference Kubrak and PrikhodkoKP21, Theorem 4.3.25, Remark 4.1.15].
$\ell \neq p$
follows from [Reference van den Bogaart and EdixhovenvdBE05, Proposition 3.1] and about being crystalline at p from [Reference Kubrak and PrikhodkoKP21, Theorem 4.3.25, Remark 4.1.15].
In the following lemma, we will use the notation
![]() $[-]$
to denote shifts of complexes. (Apart from this, we use it for torsion parts of abelian groups.)
$[-]$
to denote shifts of complexes. (Apart from this, we use it for torsion parts of abelian groups.)
Lemma 2.5. Let k be a finite field or an algebraically closed field. Let
![]() $\ell $
be a prime invertible in k. Let
$\ell $
be a prime invertible in k. Let
![]() $f \colon Y \to X$
be a morphism of separated DM stacks over
$f \colon Y \to X$
be a morphism of separated DM stacks over
![]() $\operatorname {\mathrm {Spec}} (k)$
. We assume that X and Y are smooth of pure dimension d over
$\operatorname {\mathrm {Spec}} (k)$
. We assume that X and Y are smooth of pure dimension d over
![]() $\operatorname {\mathrm {Spec}} (k)$
. We further assume that f is representable by schemes and proper, and that f is finite étale of constant degree m over a dense open substack of X. We set
$\operatorname {\mathrm {Spec}} (k)$
. We further assume that f is representable by schemes and proper, and that f is finite étale of constant degree m over a dense open substack of X. We set
![]() $\Lambda :=\mathbb Z/\ell ^n \mathbb Z$
, and let
$\Lambda :=\mathbb Z/\ell ^n \mathbb Z$
, and let
![]() $\Lambda _X$
and
$\Lambda _X$
and
![]() $\Lambda _Y$
denote the corresponding constant sheaves on X and Y, respectively.
$\Lambda _Y$
denote the corresponding constant sheaves on X and Y, respectively.
-
1. The dualizing complexes of X and Y (in the sense of [Reference Laszlo and OlssonLO08, Definition 3.4.5]) are isomorphic to
 $\Lambda _X(d)[2d]$
and
$\Lambda _X(d)[2d]$
and
 $\Lambda _Y(d)[2d]$
, respectively. We have a canonical trace morphism
$\Lambda _Y(d)[2d]$
, respectively. We have a canonical trace morphism  $$\begin{align*}\mathrm{tr}_f \colon R f_* \Lambda_Y(d)[2d] \to \Lambda_X(d)[2d]. \end{align*}$$
$$\begin{align*}\mathrm{tr}_f \colon R f_* \Lambda_Y(d)[2d] \to \Lambda_X(d)[2d]. \end{align*}$$
-
2. The composition
is equal to the multiplication by m. $$\begin{align*}\Phi \colon \Lambda_X(d) \to R f_*\Lambda_Y(d) \overset{\mathrm{tr}_f[-2d]}{\longrightarrow} \Lambda_X(d) \end{align*}$$
$$\begin{align*}\Phi \colon \Lambda_X(d) \to R f_*\Lambda_Y(d) \overset{\mathrm{tr}_f[-2d]}{\longrightarrow} \Lambda_X(d) \end{align*}$$
Proof. (1) The first assertion follows from [Reference Laszlo and OlssonLO08, Corollary 4.6.2]. We recall that the functors
![]() $Rf_!$
and
$Rf_!$
and
![]() $f^!$
are defined in [Reference Laszlo and OlssonLO08, Definition 4.4.1], which satisfy the usual adjunction property; see [Reference Laszlo and OlssonLO08, Proposition 4.4.2]. We have
$f^!$
are defined in [Reference Laszlo and OlssonLO08, Definition 4.4.1], which satisfy the usual adjunction property; see [Reference Laszlo and OlssonLO08, Proposition 4.4.2]. We have
![]() $f^!\Lambda _X(d)[2d] = \Lambda _Y(d)[2d]$
(see [Reference Laszlo and OlssonLO08, (4.4.i)]). By [Reference Laszlo and OlssonLO08, Proposition 5.2.1], we have
$f^!\Lambda _X(d)[2d] = \Lambda _Y(d)[2d]$
(see [Reference Laszlo and OlssonLO08, (4.4.i)]). By [Reference Laszlo and OlssonLO08, Proposition 5.2.1], we have
![]() $ Rf_!=Rf_*. $
Then
$ Rf_!=Rf_*. $
Then
![]() $\mathrm {tr}_f$
is defined as the following composition:
$\mathrm {tr}_f$
is defined as the following composition:
where the last morphism is induced by adjunction.
(2) We may work étale locally on X. We may thus assume that X is a scheme and k is algebraically closed. Then Y is also a scheme. It suffices to show that the induced homomorphism
is equal to the multiplication by m. Let
![]() $U \subset X$
be an open dense subscheme such that f is finite étale over U. Since U and X have the same connected components, we have
$U \subset X$
be an open dense subscheme such that f is finite étale over U. Since U and X have the same connected components, we have
![]() $H^0_{\operatorname {\acute {e}t}}(X, \Lambda (d))=H^0_{\operatorname {\acute {e}t}}(U, \Lambda (d))$
. (We note that since k is algebraically closed, we may identify
$H^0_{\operatorname {\acute {e}t}}(X, \Lambda (d))=H^0_{\operatorname {\acute {e}t}}(U, \Lambda (d))$
. (We note that since k is algebraically closed, we may identify
![]() $\Lambda (d)$
with the constant sheaf
$\Lambda (d)$
with the constant sheaf
![]() $\Lambda $
.) The assertion now follows from the corresponding statement for the trace morphisms associated with finite étale morphisms of schemes.
$\Lambda $
.) The assertion now follows from the corresponding statement for the trace morphisms associated with finite étale morphisms of schemes.
Lemma 2.5 enables us to deduce the Riemann Hypothesis part of Weil conjectures for DM stacks.
Proposition 2.6. Let X be a proper and smooth DM stack over
![]() $\mathbb {F}_{q}$
. The eigenvalues of the geometric Frobenius
$\mathbb {F}_{q}$
. The eigenvalues of the geometric Frobenius
![]() $\varphi _{q}\in \operatorname {\mathrm {Gal}}(\overline {\mathbb {F}}_{q}/\mathbb {F}_{q})$
acting on
$\varphi _{q}\in \operatorname {\mathrm {Gal}}(\overline {\mathbb {F}}_{q}/\mathbb {F}_{q})$
acting on
![]() $H^{i}_{\operatorname {\acute {e}t}}(X_{\overline {\mathbb {F}}_{q}},\mathbb {Q}_{\ell })$
are algebraic integers with complex absolute value
$H^{i}_{\operatorname {\acute {e}t}}(X_{\overline {\mathbb {F}}_{q}},\mathbb {Q}_{\ell })$
are algebraic integers with complex absolute value
![]() $q^{i/2}$
.
$q^{i/2}$
.
Proof. We may assume that X is connected. Since X is smooth, it follows that X is irreducible. By [Reference Laumon and Moret-BaillyLMB00, Théorème 16.6], there exists a finite, surjective, generically étale morphism
![]() $Z \to X$
with Z a scheme. After replacing Z by an irreducible component of it (with the reduced induced structure) which dominates X, we may assume that Z is integral. Since
$Z \to X$
with Z a scheme. After replacing Z by an irreducible component of it (with the reduced induced structure) which dominates X, we may assume that Z is integral. Since
![]() $\mathbb {F}_{q}$
is perfect, by [Reference de JongdJ96, Theorem 4.1], there exists a proper and generically finite étale morphism
$\mathbb {F}_{q}$
is perfect, by [Reference de JongdJ96, Theorem 4.1], there exists a proper and generically finite étale morphism
![]() $Y \to Z$
such that Y is a connected proper smooth scheme over
$Y \to Z$
such that Y is a connected proper smooth scheme over
![]() $\mathbb {F}_{q}$
. The composition
$\mathbb {F}_{q}$
. The composition
![]() $f \colon Y \to X$
satisfies the conditions in Lemma 2.5. Thus, the trace morphism induces a homomorphism
$f \colon Y \to X$
satisfies the conditions in Lemma 2.5. Thus, the trace morphism induces a homomorphism
such that the composition
is equal to the multiplication by some positive integer, and hence is an isomorphism. It follows that
![]() $H^i_{\operatorname {\acute {e}t}}(X_{\overline {\mathbb {F}}_{q}}, \mathbb Q_\ell )$
is isomorphic to a direct summand of
$H^i_{\operatorname {\acute {e}t}}(X_{\overline {\mathbb {F}}_{q}}, \mathbb Q_\ell )$
is isomorphic to a direct summand of
![]() $H^i_{\operatorname {\acute {e}t}}(Y_{\overline {\mathbb {F}}_{q}}, \mathbb Q_\ell )$
as a representation of
$H^i_{\operatorname {\acute {e}t}}(Y_{\overline {\mathbb {F}}_{q}}, \mathbb Q_\ell )$
as a representation of
![]() $\operatorname {\mathrm {Gal}}(\overline {\mathbb {F}}_{q}/\mathbb {F}_{q})$
. Therefore, the desired assertion follows from the Weil conjecture for schemes proved by Deligne [Reference DeligneDel73, Reference DeligneDel80].
$\operatorname {\mathrm {Gal}}(\overline {\mathbb {F}}_{q}/\mathbb {F}_{q})$
. Therefore, the desired assertion follows from the Weil conjecture for schemes proved by Deligne [Reference DeligneDel73, Reference DeligneDel80].
We also record the following statement which will facilitate the passage between statements concerning the Brauer group over
![]() $\overline {\mathbb {Q}}$
and
$\overline {\mathbb {Q}}$
and
![]() $\mathbb {C}.$
$\mathbb {C}.$
Lemma 2.7. Let K be an algebraically closed field of characteristic
![]() $0$
such that
$0$
such that
![]() $K\subset \mathbb {C}.$
Let
$K\subset \mathbb {C}.$
Let
![]() $X\rightarrow \operatorname {\mathrm {Spec}}(K)$
be a connected proper smooth DM stack. There is an exact sequence
$X\rightarrow \operatorname {\mathrm {Spec}}(K)$
be a connected proper smooth DM stack. There is an exact sequence
where
![]() $\operatorname {\mathrm {Br}}(X)^{0}\simeq (\mathbb {Q}/\mathbb Z)^{b_{2}-\rho }$
with
$\operatorname {\mathrm {Br}}(X)^{0}\simeq (\mathbb {Q}/\mathbb Z)^{b_{2}-\rho }$
with
![]() $b_{2}(X)=\dim _{\mathbb {Q}_{\ell }}H^{2}_{\operatorname {\acute {e}t}}(X, \mathbb {Q}_{\ell })$
and
$b_{2}(X)=\dim _{\mathbb {Q}_{\ell }}H^{2}_{\operatorname {\acute {e}t}}(X, \mathbb {Q}_{\ell })$
and
![]() $\rho (X)$
is the rank of the Néron-Severi group
$\rho (X)$
is the rank of the Néron-Severi group
![]() $\operatorname {\mathrm {NS}}(X)$
. Here,
$\operatorname {\mathrm {NS}}(X)$
. Here,
![]() $X_{\mathbb {C}}^{\operatorname {\mathrm {an}}}$
is the complex analytification of
$X_{\mathbb {C}}^{\operatorname {\mathrm {an}}}$
is the complex analytification of
![]() $X_{\mathbb {C}}$
.
$X_{\mathbb {C}}$
.
Proof. For schemes, this is [Reference Colliot-Thélène and SkorobogatovCTS21, Proposition 4.2.6 (ii), (iii)]. Let us quickly explain how to adapt this to the setting here.
By [Reference BrochardBro09, Théorème 4.3.1], the identity component
![]() $\underline {\operatorname {\mathrm {Pic}}}^{\circ }_{X/K}$
is a connected proper group scheme over K, so that
$\underline {\operatorname {\mathrm {Pic}}}^{\circ }_{X/K}$
is a connected proper group scheme over K, so that
![]() $\underline {\operatorname {\mathrm {Pic}}}^{\circ }_{X/K,\mathrm {red}}$
is an abelian variety over K. (In fact, since K is characteristic
$\underline {\operatorname {\mathrm {Pic}}}^{\circ }_{X/K,\mathrm {red}}$
is an abelian variety over K. (In fact, since K is characteristic
![]() $0$
, we have
$0$
, we have
![]() $\underline {\operatorname {\mathrm {Pic}}}^{\circ }_{X/K}=\underline {\operatorname {\mathrm {Pic}}}^{\circ }_{X/K,\mathrm {red}}$
by Cartier’s theorem, but we do not need this fact.) The Kummer exact sequence together with divisibility of
$\underline {\operatorname {\mathrm {Pic}}}^{\circ }_{X/K}=\underline {\operatorname {\mathrm {Pic}}}^{\circ }_{X/K,\mathrm {red}}$
by Cartier’s theorem, but we do not need this fact.) The Kummer exact sequence together with divisibility of
![]() $\underline {\operatorname {\mathrm {Pic}}}^{\circ }_{X/K,\mathrm {red}}(K)$
gives
$\underline {\operatorname {\mathrm {Pic}}}^{\circ }_{X/K,\mathrm {red}}(K)$
gives
for any prime
![]() $\ell $
. This is an exact sequence of finite abelian groups ([Reference OlssonOls07, Theorem 9.10]), so that passing to the limit we get an exact sequence
$\ell $
. This is an exact sequence of finite abelian groups ([Reference OlssonOls07, Theorem 9.10]), so that passing to the limit we get an exact sequence
where
![]() $T_{\ell }(\operatorname {\mathrm {Br}}(X))=\lim _{\cdot \ell }\operatorname {\mathrm {Br}}(X)[\ell ^{n}]$
is the
$T_{\ell }(\operatorname {\mathrm {Br}}(X))=\lim _{\cdot \ell }\operatorname {\mathrm {Br}}(X)[\ell ^{n}]$
is the
![]() $\ell $
-adic Tate module of
$\ell $
-adic Tate module of
![]() $\operatorname {\mathrm {Br}}(X)$
.
$\operatorname {\mathrm {Br}}(X)$
.
The
![]() $\mathbb {Z}_{\ell }$
-module
$\mathbb {Z}_{\ell }$
-module
![]() $T_{\ell }(\operatorname {\mathrm {Br}}(X))$
is finitely generated, since
$T_{\ell }(\operatorname {\mathrm {Br}}(X))$
is finitely generated, since
![]() $H^{2}_{\operatorname {\acute {e}t}}(X,\mathbb {Z}_{\ell }(1))$
is, and as
$H^{2}_{\operatorname {\acute {e}t}}(X,\mathbb {Z}_{\ell }(1))$
is, and as
![]() $T_{\ell }(\operatorname {\mathrm {Br}}(X))=\operatorname {\mathrm {Hom}}(\mathbb {Q}_{\ell }/\mathbb Z_{\ell },\operatorname {\mathrm {Br}}(X))$
, this is a finite free
$T_{\ell }(\operatorname {\mathrm {Br}}(X))=\operatorname {\mathrm {Hom}}(\mathbb {Q}_{\ell }/\mathbb Z_{\ell },\operatorname {\mathrm {Br}}(X))$
, this is a finite free
![]() $\mathbb Z_{\ell }$
-module, so it follows that
$\mathbb Z_{\ell }$
-module, so it follows that
![]() $T_{\ell }(\operatorname {\mathrm {Br}}(X))=\mathbb Z_{\ell }^{b_{2}-\rho }.$
Looking now at the Kummer exact sequence for
$T_{\ell }(\operatorname {\mathrm {Br}}(X))=\mathbb Z_{\ell }^{b_{2}-\rho }.$
Looking now at the Kummer exact sequence for
![]() $H^{3}$
and using that
$H^{3}$
and using that
![]() $\operatorname {\mathrm {Br}}(X)=H^{2}(X,\mathbb {G}_{m})$
is torsion ([Reference Antieau and MeierAM20, Proposition 2.5 (iii)]) and running over all
$\operatorname {\mathrm {Br}}(X)=H^{2}(X,\mathbb {G}_{m})$
is torsion ([Reference Antieau and MeierAM20, Proposition 2.5 (iii)]) and running over all
![]() $\ell $
, we obtain an exact sequence
$\ell $
, we obtain an exact sequence
Using independence of choice of algebraically closed base field (use [Sta22, Tag 07BV] and smooth base change [Reference ZhengZhe15, Proposition 2.12]) and étale-Betti comparison (see e.g. [Reference Kubrak and PrikhodkoKP21, Proposition 4.1.6]), we obtain that
![]() $ \bigoplus _{\ell } H^{3}_{\operatorname {\acute {e}t}}(X,\mathbb Z_{\ell }(1))_{\operatorname {\mathrm {tors}}}\simeq H^{3}(X_{\mathbb {C}}^{\operatorname {\mathrm {an}}},\mathbb Z)_{\operatorname {\mathrm {tors}}}. $
$ \bigoplus _{\ell } H^{3}_{\operatorname {\acute {e}t}}(X,\mathbb Z_{\ell }(1))_{\operatorname {\mathrm {tors}}}\simeq H^{3}(X_{\mathbb {C}}^{\operatorname {\mathrm {an}}},\mathbb Z)_{\operatorname {\mathrm {tors}}}. $
The next result is in the setting of schemes a classical result due to Abrashkin and Fontaine ([Reference AbrashkinAbr90], [Reference FontaineFon93]).
Theorem 2.8. Let
![]() $X\rightarrow \operatorname {\mathrm {Spec}}(\mathbb Z)$
be a proper and smooth DM stack. Then
$X\rightarrow \operatorname {\mathrm {Spec}}(\mathbb Z)$
be a proper and smooth DM stack. Then
for all
![]() $i+j\leq 3$
,
$i+j\leq 3$
,
![]() $i\neq j.$
$i\neq j.$
Proof. The argument here just uses extensions of p-adic Hodge theory to stacks and then copy-pastes the argument of Abrashkin and Fontaine. More precisely, let
![]() $V:=H^{N}_{\operatorname {\acute {e}t}}(X_{\overline {\mathbb {Q}}},\mathbb {Q}_{p}).$
Assume that there is a
$V:=H^{N}_{\operatorname {\acute {e}t}}(X_{\overline {\mathbb {Q}}},\mathbb {Q}_{p}).$
Assume that there is a
![]() $\mathbb {Q}_p[\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})]$
-filtration
$\mathbb {Q}_p[\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})]$
-filtration
such that for all
![]() $0\leq i \leq N,$
we have
$0\leq i \leq N,$
we have
![]() $V_{i}/V_{i+1}\simeq \mathbb {Q}_{p}(i)^{s_{i}}$
for some
$V_{i}/V_{i+1}\simeq \mathbb {Q}_{p}(i)^{s_{i}}$
for some
![]() $s_{i}\geq 0$
. Then, by using the de Rham comparison for DM stacks [Bog08] (this can also be deduced from [Reference Kubrak and PrikhodkoKP21, Theorem 4.3.25], c.f. loc.cit., beginning of page 9) and Proposition 2.6, we can repeat the arguments in [Reference FontaineFon93, page 4] and [Reference AbrashkinAbr14, Proposition 5.3] to conclude that
$s_{i}\geq 0$
. Then, by using the de Rham comparison for DM stacks [Bog08] (this can also be deduced from [Reference Kubrak and PrikhodkoKP21, Theorem 4.3.25], c.f. loc.cit., beginning of page 9) and Proposition 2.6, we can repeat the arguments in [Reference FontaineFon93, page 4] and [Reference AbrashkinAbr14, Proposition 5.3] to conclude that
for
![]() $i+j\leq N$
,
$i+j\leq N$
,
![]() $i\neq j.$
Namely, de Rham comparison implies that we have
$i\neq j.$
Namely, de Rham comparison implies that we have
Let
![]() $\ell \neq p$
be a prime. Since
$\ell \neq p$
be a prime. Since
![]() $X_{\mathbb {F}_{\ell }}\rightarrow \operatorname {\mathrm {Spec}}(\mathbb {F}_{\ell })$
is proper and smooth, it follows by Proposition 2.6 that
$X_{\mathbb {F}_{\ell }}\rightarrow \operatorname {\mathrm {Spec}}(\mathbb {F}_{\ell })$
is proper and smooth, it follows by Proposition 2.6 that
![]() $\varphi _{\ell }$
acts on V with eigenvalues
$\varphi _{\ell }$
acts on V with eigenvalues
![]() $\lambda ,$
such that
$\lambda ,$
such that
![]() $|\lambda |=\ell ^{N/2}.$
However,
$|\lambda |=\ell ^{N/2}.$
However,
![]() $\varphi _{\ell }$
acts by multiplication with
$\varphi _{\ell }$
acts by multiplication with
![]() $\ell ^{i}$
on
$\ell ^{i}$
on
![]() $\mathbb {Q}_{p}(i).$
This implies that the group
$\mathbb {Q}_{p}(i).$
This implies that the group
![]() $H^{i}(X_{\mathbb {C}},\Omega ^{j}_{X_{\mathbb {C}}/\mathbb {C}})$
for
$H^{i}(X_{\mathbb {C}},\Omega ^{j}_{X_{\mathbb {C}}/\mathbb {C}})$
for
![]() $i+j=N$
can only be nonzero if
$i+j=N$
can only be nonzero if
![]() $\ell ^{i}=\ell ^{N/2},$
as desired.
$\ell ^{i}=\ell ^{N/2},$
as desired.
It suffices therefore to find such a filtration. For this, we can just cite Fontaine [Reference FontaineFon93, Proposition 1].
Remark 2.9. Theorem 2.8 implies that
and
When applied to
![]() $X=\overline {\mathcal {M}}_{g,n}$
this gives a p-adic Hodge theory approach to (some of) the classical vanishing results in [Reference Arbarello and CornalbaAC98] (with the exception of the degree
$X=\overline {\mathcal {M}}_{g,n}$
this gives a p-adic Hodge theory approach to (some of) the classical vanishing results in [Reference Arbarello and CornalbaAC98] (with the exception of the degree
![]() $5$
cohomology).
$5$
cohomology).
3 General results on Brauer groups of proper and smooth Deligne-Mumford stacks over the integers
3.1 Finiteness of the Brauer group
In this subsection, we shall prove that the Brauer groups
![]() $ \operatorname {\mathrm {Br}}(X) $
and
$ \operatorname {\mathrm {Br}}(X) $
and
![]() $ \operatorname {\mathrm {Br}}(X_{\overline {\mathbb Q}}) $
are finite for a proper and smooth DM stack X over
$ \operatorname {\mathrm {Br}}(X_{\overline {\mathbb Q}}) $
are finite for a proper and smooth DM stack X over
![]() $\operatorname {\mathrm {Spec}}(\mathbb Z)$
; see Theorem 3.4.
$\operatorname {\mathrm {Spec}}(\mathbb Z)$
; see Theorem 3.4.
For this, we will need to use the relative Picard functor. Let S be a noetherian scheme and let
![]() $f\colon X\rightarrow S$
be a proper DM stack over S. We assume that f is flat and
$f\colon X\rightarrow S$
be a proper DM stack over S. We assume that f is flat and
![]() $\mathcal {O}_{S}\simeq f_{*}\mathcal {O}_{X}$
holds universally; that is, the same holds for the base change
$\mathcal {O}_{S}\simeq f_{*}\mathcal {O}_{X}$
holds universally; that is, the same holds for the base change
![]() $X \times _S T \to T$
along any morphism
$X \times _S T \to T$
along any morphism
![]() $T \to S$
of schemes. (By Lemma 3.3, this holds if f is smooth,
$T \to S$
of schemes. (By Lemma 3.3, this holds if f is smooth,
![]() $S=\operatorname {\mathrm {Spec}} \mathbb Z$
, and X is connected.) We denote by
$S=\operatorname {\mathrm {Spec}} \mathbb Z$
, and X is connected.) We denote by
![]() $\underline {\operatorname {\mathrm {Pic}}}_{X/S}$
the relative Picard functor; that is, the fppf sheafification of the presheaf that sends a (quasi-separated) scheme T over S to
$\underline {\operatorname {\mathrm {Pic}}}_{X/S}$
the relative Picard functor; that is, the fppf sheafification of the presheaf that sends a (quasi-separated) scheme T over S to
Then this is representable by a commutative group algebraic space locally of finite type over S and its formation commutes with base change in S by [Reference BrochardBro09, Théorème 1.1, Proposition 2.3.3] and [Reference Fringuelli and VivianiFV23, Theorem 3.1]. We note that by [Reference BrochardBro09, Théorème 2.2.6], we could also work with the étale sheafification. See [Reference Fringuelli and VivianiFV23, Section 3], [Reference BrochardBro09], [Reference BrochardBro12] for background that is needed in our work.
Remark 3.1. In fact, we will mostly consider morphisms
![]() $f\colon X\rightarrow \operatorname {\mathrm {Spec}}(\mathbb Z)$
which will be proper and smooth. For such morphisms,
$f\colon X\rightarrow \operatorname {\mathrm {Spec}}(\mathbb Z)$
which will be proper and smooth. For such morphisms,
![]() $f_{*}\mathcal {O}_{X}$
is locally free on
$f_{*}\mathcal {O}_{X}$
is locally free on
![]() $\operatorname {\mathrm {Spec}}(\mathbb Z)$
, and its formation commutes with base change along any morphism
$\operatorname {\mathrm {Spec}}(\mathbb Z)$
, and its formation commutes with base change along any morphism
![]() $T \to \operatorname {\mathrm {Spec}}(\mathbb Z)$
. This is a special case of the following more general result, which we record here for the convenience of the reader.
$T \to \operatorname {\mathrm {Spec}}(\mathbb Z)$
. This is a special case of the following more general result, which we record here for the convenience of the reader.
Lemma 3.2. Let
![]() $S=\operatorname {\mathrm {Spec}}(A)$
with A a noetherian ring of finite global cohomological dimension. We assume that S is reduced and connected. Let
$S=\operatorname {\mathrm {Spec}}(A)$
with A a noetherian ring of finite global cohomological dimension. We assume that S is reduced and connected. Let
![]() $f \colon X \to S$
be a proper and flat DM stack over S such that every geometric fiber is normal. Then
$f \colon X \to S$
be a proper and flat DM stack over S such that every geometric fiber is normal. Then
![]() $f_{*}\mathcal {O}_{X}$
is locally free on S, and its formation commutes with base change along any morphism
$f_{*}\mathcal {O}_{X}$
is locally free on S, and its formation commutes with base change along any morphism
![]() $T \to S$
.
$T \to S$
.
Proof. It is well known that the function sending a point
![]() $s \in S$
to the number of connected components of the geometric fiber of X at s is constant (cf., [Reference Deligne and MumfordDM69, Theorem 4.17]). Then, the assertion follows by the same argument as in the proof of [Reference MumfordMum85, Chapter II, Section 5, Corollary 2] with the following modification. We first remark that since X is stack, we cannot expect the existence of a bounded complex of finite projective A-modules which computes the cohomology groups of
$s \in S$
to the number of connected components of the geometric fiber of X at s is constant (cf., [Reference Deligne and MumfordDM69, Theorem 4.17]). Then, the assertion follows by the same argument as in the proof of [Reference MumfordMum85, Chapter II, Section 5, Corollary 2] with the following modification. We first remark that since X is stack, we cannot expect the existence of a bounded complex of finite projective A-modules which computes the cohomology groups of
![]() $\mathcal {O}_X$
universally, in contrast to the case of schemes, where such a complex is constructed in [Reference MumfordMum85, Chapter II, Section 5]. Instead, under the assumption that A is of finite global cohomological dimension, we can find a two term complex
$\mathcal {O}_X$
universally, in contrast to the case of schemes, where such a complex is constructed in [Reference MumfordMum85, Chapter II, Section 5]. Instead, under the assumption that A is of finite global cohomological dimension, we can find a two term complex
![]() $K^\bullet $
of finite projective A-modules
$K^\bullet $
of finite projective A-modules
such that
![]() $H^0(K^\bullet \otimes _A B) \simeq H^{0}(X_{B},\mathcal {O}_{X_{B}})$
for any A-algebra B and it is functorial in B. This follows from [Reference BrochardBro12, Corollary A.2.4]. We can then follow the argument in [Reference MumfordMum85, Chapter II, Section 5, Corollary 2] to deduce the desired claim.
$H^0(K^\bullet \otimes _A B) \simeq H^{0}(X_{B},\mathcal {O}_{X_{B}})$
for any A-algebra B and it is functorial in B. This follows from [Reference BrochardBro12, Corollary A.2.4]. We can then follow the argument in [Reference MumfordMum85, Chapter II, Section 5, Corollary 2] to deduce the desired claim.
Let us record the following consequence of Remark 3.1.
Lemma 3.3. For a proper and smooth DM stack
![]() $X \to \operatorname {\mathrm {Spec}}(\mathbb Z)$
, the following assertions are equivalent:
$X \to \operatorname {\mathrm {Spec}}(\mathbb Z)$
, the following assertions are equivalent:
-
1. We have
 $\mathcal {O}_{\operatorname {\mathrm {Spec}}(\mathbb Z)}\simeq f_{*}\mathcal {O}_{X}$
universally.
$\mathcal {O}_{\operatorname {\mathrm {Spec}}(\mathbb Z)}\simeq f_{*}\mathcal {O}_{X}$
universally. -
2. The geometric fibers of X are connected.
-
3. X is connected.
Proof. If
![]() $\mathcal {O}_{\operatorname {\mathrm {Spec}}(\mathbb Z)}\simeq f_{*}\mathcal {O}_{X}$
holds universally, then for any point
$\mathcal {O}_{\operatorname {\mathrm {Spec}}(\mathbb Z)}\simeq f_{*}\mathcal {O}_{X}$
holds universally, then for any point
![]() $s \in \operatorname {\mathrm {Spec}}(\mathbb Z)$
, we see that
$s \in \operatorname {\mathrm {Spec}}(\mathbb Z)$
, we see that
![]() $H^0(X_s, \mathcal {O}_{X_s})$
is a
$H^0(X_s, \mathcal {O}_{X_s})$
is a
![]() $1$
-dimensional vector space over the residue field of s. Thus, (1) implies (2).
$1$
-dimensional vector space over the residue field of s. Thus, (1) implies (2).
![]() $(2) \Rightarrow (3)$
is easy. It remains to show that (3) implies (1). If we show that
$(2) \Rightarrow (3)$
is easy. It remains to show that (3) implies (1). If we show that
![]() $\mathbb Z=H^{0}(X,\mathcal {O}_{X})$
, then universality follows from Remark 3.1. It is easy to see that
$\mathbb Z=H^{0}(X,\mathcal {O}_{X})$
, then universality follows from Remark 3.1. It is easy to see that
![]() $H^{0}(X,\mathcal {O}_{X})$
is finite and flat over
$H^{0}(X,\mathcal {O}_{X})$
is finite and flat over
![]() $\mathbb Z$
. Then, Remark 3.1 implies that
$\mathbb Z$
. Then, Remark 3.1 implies that
![]() $H^{0}(X,\mathcal {O}_{X})$
is finite and étale over
$H^{0}(X,\mathcal {O}_{X})$
is finite and étale over
![]() $\mathbb Z$
. It follows from Minkowski’s theorem that
$\mathbb Z$
. It follows from Minkowski’s theorem that
![]() $\mathbb Z=H^{0}(X,\mathcal {O}_{X})$
when X is connected.
$\mathbb Z=H^{0}(X,\mathcal {O}_{X})$
when X is connected.
Let us now explain the following result:
Theorem 3.4. Let
![]() $f\colon X\rightarrow \operatorname {\mathrm {Spec}}(\mathbb Z)$
be a proper and smooth DM stack. Then
$f\colon X\rightarrow \operatorname {\mathrm {Spec}}(\mathbb Z)$
be a proper and smooth DM stack. Then
![]() $ \operatorname {\mathrm {Br}}(X) $
and
$ \operatorname {\mathrm {Br}}(X) $
and
![]() $ \operatorname {\mathrm {Br}}(X_{\overline {\mathbb Q}}) $
are finite.
$ \operatorname {\mathrm {Br}}(X_{\overline {\mathbb Q}}) $
are finite.
Proof. Since we do not need this result in the following, we will only sketch the proof. First observe that
![]() $b_{2}(X_{\overline {\mathbb Q}})=\rho (X_{\overline {\mathbb Q}})$
by Theorem 2.8. Thus, Lemma 2.7 implies that
$b_{2}(X_{\overline {\mathbb Q}})=\rho (X_{\overline {\mathbb Q}})$
by Theorem 2.8. Thus, Lemma 2.7 implies that
![]() $ \operatorname {\mathrm {Br}}(X_{\overline {\mathbb Q}}) $
is finite. For the finiteness of
$ \operatorname {\mathrm {Br}}(X_{\overline {\mathbb Q}}) $
is finite. For the finiteness of
![]() $ \operatorname {\mathrm {Br}}(X) $
, we may assume that X is connected. Then, by Lemma 3.3, we have
$ \operatorname {\mathrm {Br}}(X) $
, we may assume that X is connected. Then, by Lemma 3.3, we have
![]() $\mathcal {O}_{\operatorname {\mathrm {Spec}}(\mathbb Z)}\simeq f_{*}\mathcal {O}_{X}$
universally, so that we can use the relative Picard space
$\mathcal {O}_{\operatorname {\mathrm {Spec}}(\mathbb Z)}\simeq f_{*}\mathcal {O}_{X}$
universally, so that we can use the relative Picard space
![]() $\underline {\operatorname {\mathrm {Pic}}}_{X/\mathbb Z}$
in the following.
$\underline {\operatorname {\mathrm {Pic}}}_{X/\mathbb Z}$
in the following.
Since
![]() $\operatorname {\mathrm {Br}}(X_{\overline {\mathbb {Q}}})$
is finite, it follows that
$\operatorname {\mathrm {Br}}(X_{\overline {\mathbb {Q}}})$
is finite, it follows that
![]() $\operatorname {\mathrm {Br}}(X_{\overline {\mathbb Z}})$
is also finite. We therefore have to see that
$\operatorname {\mathrm {Br}}(X_{\overline {\mathbb Z}})$
is also finite. We therefore have to see that
is finite. It follows from Theorem 2.8 that there exists a dense open subset U of
![]() $\operatorname {\mathrm {Spec}}(\mathbb Z)$
such that for all
$\operatorname {\mathrm {Spec}}(\mathbb Z)$
such that for all
![]() $s\in U,$
$s\in U,$
for
![]() $i=1,2,3$
(where
$i=1,2,3$
(where
![]() $X_s$
is the fiber of X at s). By [Reference Fringuelli and VivianiFV23, Proposition 3.2, Theorem 3.6], the relative Picard space
$X_s$
is the fiber of X at s). By [Reference Fringuelli and VivianiFV23, Proposition 3.2, Theorem 3.6], the relative Picard space
![]() $\underline {\operatorname {\mathrm {Pic}}}_{X_{U}/U}$
is étale over U. We have an exact sequence of abelian sheaves for the fppf topology on U:
$\underline {\operatorname {\mathrm {Pic}}}_{X_{U}/U}$
is étale over U. We have an exact sequence of abelian sheaves for the fppf topology on U:
By ([Reference Fringuelli and VivianiFV23, Theorem 3.6 (iv) (b)]),
![]() $\underline {\operatorname {\mathrm {Pic}}}^{\tau }_{X_{U}/U}$
is proper over U, and since it is open in
$\underline {\operatorname {\mathrm {Pic}}}^{\tau }_{X_{U}/U}$
is proper over U, and since it is open in
![]() $\underline {\operatorname {\mathrm {Pic}}}_{X_{U}/U}$
[Reference Fringuelli and VivianiFV23, Theorem 3.6 (i)], it is finite étale. It follows from [Reference MilneMil86, Theorem 3.1] that
$\underline {\operatorname {\mathrm {Pic}}}_{X_{U}/U}$
[Reference Fringuelli and VivianiFV23, Theorem 3.6 (i)], it is finite étale. It follows from [Reference MilneMil86, Theorem 3.1] that
![]() $H^{i}_{\text {fl}}(U,\underline {\operatorname {\mathrm {Pic}}}^{\tau }_{X_{U}/U})$
is finite. Furthermore,
$H^{i}_{\text {fl}}(U,\underline {\operatorname {\mathrm {Pic}}}^{\tau }_{X_{U}/U})$
is finite. Furthermore,
![]() $\text {Num}_{X_{U}/U}$
is a locally constant étale sheaf of finite free
$\text {Num}_{X_{U}/U}$
is a locally constant étale sheaf of finite free
![]() $\mathbb Z$
-modules (cf., the proof of Lemma 3.11). It is then not too hard to see that
$\mathbb Z$
-modules (cf., the proof of Lemma 3.11). It is then not too hard to see that
![]() $H^{1}_{\text {fl}}(U,\text {Num}_{X_{U}/U})$
is finite. We deduce then that also
$H^{1}_{\text {fl}}(U,\text {Num}_{X_{U}/U})$
is finite. We deduce then that also
![]() $H^{1}_{\text {fl}}(U,\underline {\operatorname {\mathrm {Pic}}}_{X_{U}/U})$
is finite. Now we look at the 7 term exact sequence (see, for example, [Reference MilneMil80, Appendix B, page 309]) for the Leray spectral sequence in the fppf topology for
$H^{1}_{\text {fl}}(U,\underline {\operatorname {\mathrm {Pic}}}_{X_{U}/U})$
is finite. Now we look at the 7 term exact sequence (see, for example, [Reference MilneMil80, Appendix B, page 309]) for the Leray spectral sequence in the fppf topology for
![]() $f_{U}\colon X_{U}\rightarrow U$
and the sheaf
$f_{U}\colon X_{U}\rightarrow U$
and the sheaf
![]() $\mathbb {G}_{m}$
and see that
$\mathbb {G}_{m}$
and see that
is finite. Here,
![]() $\overline {U}=U\times _{\operatorname {\mathrm {Spec}}(\mathbb Z)}\operatorname {\mathrm {Spec}}(\overline {\mathbb Z}).$
It then suffices to see that
$\overline {U}=U\times _{\operatorname {\mathrm {Spec}}(\mathbb Z)}\operatorname {\mathrm {Spec}}(\overline {\mathbb Z}).$
It then suffices to see that
![]() $K_{\mathbb Z}\cap \operatorname {\mathrm {Im}}(\operatorname {\mathrm {Br}}(U))$
(intersection in
$K_{\mathbb Z}\cap \operatorname {\mathrm {Im}}(\operatorname {\mathrm {Br}}(U))$
(intersection in
![]() $\operatorname {\mathrm {Br}}(X_{U})$
) is finite. This is not too hard to see using that X acquires a
$\operatorname {\mathrm {Br}}(X_{U})$
) is finite. This is not too hard to see using that X acquires a
![]() $\mathcal {O}_{K}$
-valued point, where
$\mathcal {O}_{K}$
-valued point, where
![]() $K/\mathbb {Q}$
is some finite Galois extension, and that
$K/\mathbb {Q}$
is some finite Galois extension, and that
![]() $\operatorname {\mathrm {Br}}(\mathcal {O}_{K})$
is finite ([Reference GrothendieckGro68, Proposition 2.4]).
$\operatorname {\mathrm {Br}}(\mathcal {O}_{K})$
is finite ([Reference GrothendieckGro68, Proposition 2.4]).
3.2 Deducing vanishing over the integers
The main result of this section is the following:
Proposition 3.5. Let
![]() $f\colon X\rightarrow \operatorname {\mathrm {Spec}}(\mathbb Z)$
be a proper and smooth DM stack with geometrically connected fibers. Assume that either of the following conditions holds:
$f\colon X\rightarrow \operatorname {\mathrm {Spec}}(\mathbb Z)$
be a proper and smooth DM stack with geometrically connected fibers. Assume that either of the following conditions holds:
-
1.
 $X(\mathbb Z)\neq \emptyset $
and
$X(\mathbb Z)\neq \emptyset $
and
 $X_{\overline {\mathbb {Q}}}$
is simply connected.
$X_{\overline {\mathbb {Q}}}$
is simply connected. -
2.
 $\underline {\operatorname {\mathrm {Pic}}}_{X/\mathbb Z}$
is a constant sheaf associated with a finitely generated
$\underline {\operatorname {\mathrm {Pic}}}_{X/\mathbb Z}$
is a constant sheaf associated with a finitely generated
 $\mathbb Z$
-module.
$\mathbb Z$
-module.
Then the natural homomorphism
is injective.
Before we start the proof of Proposition 3.5, we need two lemmas. Let us consider
![]() $f\colon X\rightarrow \operatorname {\mathrm {Spec}}(\mathbb Z),$
a proper and smooth DM stack with geometrically connected fibers.
$f\colon X\rightarrow \operatorname {\mathrm {Spec}}(\mathbb Z),$
a proper and smooth DM stack with geometrically connected fibers.
Lemma 3.6. Assume that
![]() $X_{\overline {\mathbb {Q}}}$
is simply connected. Then we have
$X_{\overline {\mathbb {Q}}}$
is simply connected. Then we have
Proof. Since
![]() $H^{1}(X_{\mathbb {Q}},\mathcal {O}_{X_{\mathbb {Q}}})=0$
by Theorem 2.8, we have that
$H^{1}(X_{\mathbb {Q}},\mathcal {O}_{X_{\mathbb {Q}}})=0$
by Theorem 2.8, we have that
![]() $\underline {\operatorname {\mathrm {Pic}}}^{0}_{X_{\mathbb {Q}}/\mathbb {Q}}(\overline {\mathbb {Q}})=0$
(use [Reference BrochardBro09, Théorème 4.1.3]), so that
$\underline {\operatorname {\mathrm {Pic}}}^{0}_{X_{\mathbb {Q}}/\mathbb {Q}}(\overline {\mathbb {Q}})=0$
(use [Reference BrochardBro09, Théorème 4.1.3]), so that
![]() $ \operatorname {\mathrm {Pic}}(X_{\overline {\mathbb {Q}}})=\operatorname {\mathrm {NS}}(X_{\overline {\mathbb {Q}}}). $
Thus
$ \operatorname {\mathrm {Pic}}(X_{\overline {\mathbb {Q}}})=\operatorname {\mathrm {NS}}(X_{\overline {\mathbb {Q}}}). $
Thus
![]() $\operatorname {\mathrm {Pic}}(X_{\overline {\mathbb {Q}}})$
is a finitely generated abelian group by [Reference BrochardBro12, Theorem 3.4.1]. Next, we claim that
$\operatorname {\mathrm {Pic}}(X_{\overline {\mathbb {Q}}})$
is a finitely generated abelian group by [Reference BrochardBro12, Theorem 3.4.1]. Next, we claim that
![]() $\operatorname {\mathrm {Pic}}(X_{\overline {\mathbb {Q}}})$
is torsion free under our assumptions. Namely, the Kummer exact sequence gives
$\operatorname {\mathrm {Pic}}(X_{\overline {\mathbb {Q}}})$
is torsion free under our assumptions. Namely, the Kummer exact sequence gives
a surjection
![]() $ H^{1}(X_{\overline {\mathbb {Q}}},\mu _{n}) \to \operatorname {\mathrm {Pic}}(X_{\overline {\mathbb {Q}}})[n]. $
Since we assume that
$ H^{1}(X_{\overline {\mathbb {Q}}},\mu _{n}) \to \operatorname {\mathrm {Pic}}(X_{\overline {\mathbb {Q}}})[n]. $
Since we assume that
![]() $X_{\overline {\mathbb {Q}}}$
is simply connected, it follows that
$X_{\overline {\mathbb {Q}}}$
is simply connected, it follows that
![]() $H^{1}(X_{\overline {\mathbb {Q}}},\mu _{n})=0,$
which implies that
$H^{1}(X_{\overline {\mathbb {Q}}},\mu _{n})=0,$
which implies that
![]() $\operatorname {\mathrm {Pic}}(X_{\overline {\mathbb {Q}}})$
is torsion free, as desired.
$\operatorname {\mathrm {Pic}}(X_{\overline {\mathbb {Q}}})$
is torsion free, as desired.
Now observe that
![]() $\operatorname {\mathrm {Pic}}(X_{\overline {\mathbb {Q}}})$
is an everywhere unramified representation of
$\operatorname {\mathrm {Pic}}(X_{\overline {\mathbb {Q}}})$
is an everywhere unramified representation of
![]() $\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q}).$
Namely, let
$\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q}).$
Namely, let
![]() $\ell $
be a prime, and we want to show that
$\ell $
be a prime, and we want to show that
![]() $\operatorname {\mathrm {Pic}}(X_{\overline {\mathbb {Q}}})$
is unramified at
$\operatorname {\mathrm {Pic}}(X_{\overline {\mathbb {Q}}})$
is unramified at
![]() $\ell .$
Let
$\ell .$
Let
![]() $p\neq \ell $
be an auxiliary prime. By the Kummer exact sequence and since
$p\neq \ell $
be an auxiliary prime. By the Kummer exact sequence and since
![]() $\operatorname {\mathrm {Pic}}(X_{\overline {\mathbb {Q}}})=\operatorname {\mathrm {NS}}(X_{\overline {\mathbb {Q}}}),$
as explained above, we have a
$\operatorname {\mathrm {Pic}}(X_{\overline {\mathbb {Q}}})=\operatorname {\mathrm {NS}}(X_{\overline {\mathbb {Q}}}),$
as explained above, we have a
![]() $\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$
-equivariant embedding
$\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$
-equivariant embedding
Since we know that
![]() $\operatorname {\mathrm {Pic}}(X_{\overline {\mathbb {Q}}})$
is torsion free, Lemma 2.4 implies that it is unramified at
$\operatorname {\mathrm {Pic}}(X_{\overline {\mathbb {Q}}})$
is torsion free, Lemma 2.4 implies that it is unramified at
![]() $\ell $
, as desired.
$\ell $
, as desired.
The action of
![]() $\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$
on
$\operatorname {\mathrm {Gal}}(\overline {\mathbb {Q}}/\mathbb {Q})$
on
![]() $\operatorname {\mathrm {Pic}}(X_{\overline {\mathbb {Q}}})$
is then trivial by Minkowski’s theorem. In total, it follows that
$\operatorname {\mathrm {Pic}}(X_{\overline {\mathbb {Q}}})$
is then trivial by Minkowski’s theorem. In total, it follows that
since
![]() $\operatorname {\mathrm {Pic}}(X_{\overline {\mathbb {Q}}})$
is torsion free.
$\operatorname {\mathrm {Pic}}(X_{\overline {\mathbb {Q}}})$
is torsion free.
Lemma 3.7. Assume that
![]() $X_{\overline {\mathbb {Q}}}$
is simply connected. Then
$X_{\overline {\mathbb {Q}}}$
is simply connected. Then
Proof. First observe that
![]() $\operatorname {\mathrm {Im}}(\operatorname {\mathrm {Br}}(\mathbb {Q})\rightarrow \operatorname {\mathrm {Br}}(X_{\mathbb {Q}}))$
lies in
$\operatorname {\mathrm {Im}}(\operatorname {\mathrm {Br}}(\mathbb {Q})\rightarrow \operatorname {\mathrm {Br}}(X_{\mathbb {Q}}))$
lies in
![]() $\operatorname {\mathrm {Ker}}(\operatorname {\mathrm {Br}}(X_{\mathbb {Q}})\rightarrow \operatorname {\mathrm {Br}}(X_{\overline {\mathbb {Q}}}))$
. For the reverse inclusion, we argue as follows: Since
$\operatorname {\mathrm {Ker}}(\operatorname {\mathrm {Br}}(X_{\mathbb {Q}})\rightarrow \operatorname {\mathrm {Br}}(X_{\overline {\mathbb {Q}}}))$
. For the reverse inclusion, we argue as follows: Since
![]() $R^{1}f_{*}\mathbb {G}_{m}=\underline {\operatorname {\mathrm {Pic}}}_{X/\mathbb Z}$
by [Reference BrochardBro09, Proposition 2.1.3], we have
$R^{1}f_{*}\mathbb {G}_{m}=\underline {\operatorname {\mathrm {Pic}}}_{X/\mathbb Z}$
by [Reference BrochardBro09, Proposition 2.1.3], we have
by Lemma 3.6. By the 7 term exact sequence for the Leray spectral sequence in étale cohomology for
![]() $f_{\mathbb {Q}}\colon X_{\mathbb {Q}}\rightarrow \operatorname {\mathrm {Spec}}(\mathbb {Q})$
and
$f_{\mathbb {Q}}\colon X_{\mathbb {Q}}\rightarrow \operatorname {\mathrm {Spec}}(\mathbb {Q})$
and
![]() $\mathbb {G}_{m}$
(see [Reference BrochardBro09, Théorème A.2.8.]), we then have a surjection
$\mathbb {G}_{m}$
(see [Reference BrochardBro09, Théorème A.2.8.]), we then have a surjection
(Here, we also use
![]() $\operatorname {\mathrm {Br}}(Y)=H^{2}_{\operatorname {\acute {e}t}}(Y,\mathbb {G}_{m})$
for a noetherian and regular DM stack Y.) Since
$\operatorname {\mathrm {Br}}(Y)=H^{2}_{\operatorname {\acute {e}t}}(Y,\mathbb {G}_{m})$
for a noetherian and regular DM stack Y.) Since
![]() $R^{2}f_{*}\mathbb {G}_{m}$
is an étale sheaf, we see that
$R^{2}f_{*}\mathbb {G}_{m}$
is an étale sheaf, we see that
![]() $H^{0}(\operatorname {\mathrm {Spec}}(\mathbb {Q}),R^{2}f_{*}\mathbb {G}_{m})$
is a subgroup of
$H^{0}(\operatorname {\mathrm {Spec}}(\mathbb {Q}),R^{2}f_{*}\mathbb {G}_{m})$
is a subgroup of
![]() $H^{0}(\operatorname {\mathrm {Spec}}(K),R^{2}f_{*}\mathbb {G}_{m}),$
where K is a finite extension of
$H^{0}(\operatorname {\mathrm {Spec}}(K),R^{2}f_{*}\mathbb {G}_{m}),$
where K is a finite extension of
![]() $\mathbb {Q}$
contained in
$\mathbb {Q}$
contained in
![]() $\overline {\mathbb {Q}}.$
It follows by the exactness of filtered colimits that
$\overline {\mathbb {Q}}.$
It follows by the exactness of filtered colimits that
![]() $H^{0}(\operatorname {\mathrm {Spec}}(\mathbb {Q}),R^{2}f_{*}\mathbb {G}_{m})$
is likewise a subgroup of
$H^{0}(\operatorname {\mathrm {Spec}}(\mathbb {Q}),R^{2}f_{*}\mathbb {G}_{m})$
is likewise a subgroup of
![]() $\operatorname {\mathrm {colim}}_{K/\mathbb {Q}}H^{0}(\operatorname {\mathrm {Spec}}(K),R^{2}f_{*}\mathbb {G}_{m}),$
where the colimit is indexed by finite extensions of
$\operatorname {\mathrm {colim}}_{K/\mathbb {Q}}H^{0}(\operatorname {\mathrm {Spec}}(K),R^{2}f_{*}\mathbb {G}_{m}),$
where the colimit is indexed by finite extensions of
![]() $\mathbb {Q}$
contained in
$\mathbb {Q}$
contained in
![]() $\overline {\mathbb {Q}}.$
Therefore, we have that
$\overline {\mathbb {Q}}.$
Therefore, we have that
which implies, since the map
![]() $\operatorname {\mathrm {Br}}(X_{\mathbb {Q}})\rightarrow H^{0}_{\operatorname {\acute {e}t}}(\operatorname {\mathrm {Spec}}(\overline {\mathbb {Q}}),R^{2}f_{*}\mathbb {G}_{m})$
factors over the map
$\operatorname {\mathrm {Br}}(X_{\mathbb {Q}})\rightarrow H^{0}_{\operatorname {\acute {e}t}}(\operatorname {\mathrm {Spec}}(\overline {\mathbb {Q}}),R^{2}f_{*}\mathbb {G}_{m})$
factors over the map
![]() $\operatorname {\mathrm {Br}}(X_{\mathbb {Q}})\rightarrow \operatorname {\mathrm {Br}}(X_{\overline {\mathbb {Q}}}),$
that
$\operatorname {\mathrm {Br}}(X_{\mathbb {Q}})\rightarrow \operatorname {\mathrm {Br}}(X_{\overline {\mathbb {Q}}}),$
that
Taking this together, we obtain
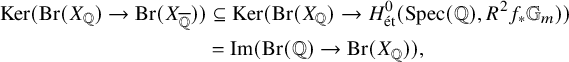 $$ \begin{align*} \operatorname{\mathrm{Ker}}(\operatorname{\mathrm{Br}}(X_{\mathbb{Q}})\rightarrow \operatorname{\mathrm{Br}}(X_{\overline{\mathbb{Q}}})) & \subseteq \operatorname{\mathrm{Ker}}(\operatorname{\mathrm{Br}}(X_{\mathbb{Q}})\rightarrow H^{0}_{\operatorname{\acute{e}t}}(\operatorname{\mathrm{Spec}}(\mathbb{Q}),R^{2}f_{*}\mathbb{G}_{m})) \\ & = \operatorname{\mathrm{Im}} (\operatorname{\mathrm{Br}}(\mathbb{Q})\rightarrow \operatorname{\mathrm{Br}}(X_{\mathbb{Q}})), \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Ker}}(\operatorname{\mathrm{Br}}(X_{\mathbb{Q}})\rightarrow \operatorname{\mathrm{Br}}(X_{\overline{\mathbb{Q}}})) & \subseteq \operatorname{\mathrm{Ker}}(\operatorname{\mathrm{Br}}(X_{\mathbb{Q}})\rightarrow H^{0}_{\operatorname{\acute{e}t}}(\operatorname{\mathrm{Spec}}(\mathbb{Q}),R^{2}f_{*}\mathbb{G}_{m})) \\ & = \operatorname{\mathrm{Im}} (\operatorname{\mathrm{Br}}(\mathbb{Q})\rightarrow \operatorname{\mathrm{Br}}(X_{\mathbb{Q}})), \end{align*} $$
as desired.
Now we can prove Proposition 3.5:
Proof of Proposition 3.5.
We first put ourselves in the situation (1). Consider a Brauer class
![]() $\alpha \in \operatorname {\mathrm {Br}}(X)$
such that
$\alpha \in \operatorname {\mathrm {Br}}(X)$
such that
![]() $\alpha \vert _{X_{\overline {\mathbb {Q}}}}=0.$
By Lemma 3.7, we have
$\alpha \vert _{X_{\overline {\mathbb {Q}}}}=0.$
By Lemma 3.7, we have
for some
![]() $\beta \in \operatorname {\mathrm {Br}}(\mathbb {Q})$
. We choose a section
$\beta \in \operatorname {\mathrm {Br}}(\mathbb {Q})$
. We choose a section
![]() $s\colon \operatorname {\mathrm {Spec}}(\mathbb Z)\rightarrow X$
of the structure map. Passing to Brauer groups, we get the following commutative diagram:
$s\colon \operatorname {\mathrm {Spec}}(\mathbb Z)\rightarrow X$
of the structure map. Passing to Brauer groups, we get the following commutative diagram:
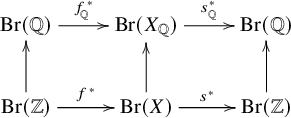
where both horizontal rows compose to the identity. We have that
![]() $\operatorname {\mathrm {Br}}(\mathbb Z)=0$
by class field theory. This implies that
$\operatorname {\mathrm {Br}}(\mathbb Z)=0$
by class field theory. This implies that
![]() $\beta =0$
, so that
$\beta =0$
, so that
![]() $\alpha \vert _{X_{\mathbb {Q}}}=0$
. This by the injectivity (see [Reference Antieau and MeierAM20, Proposition 2.5 (iv)]) of
$\alpha \vert _{X_{\mathbb {Q}}}=0$
. This by the injectivity (see [Reference Antieau and MeierAM20, Proposition 2.5 (iv)]) of
![]() $\operatorname {\mathrm {Br}}(X)\rightarrow \operatorname {\mathrm {Br}}(X_{\mathbb {Q}})$
implies that
$\operatorname {\mathrm {Br}}(X)\rightarrow \operatorname {\mathrm {Br}}(X_{\mathbb {Q}})$
implies that
![]() $\alpha =0,$
as desired.
$\alpha =0,$
as desired.
Next, we put ourselves in the situation (2). We argue as in Lemma 3.7: Using that
![]() $\operatorname {\mathrm {Br}}(\mathbb Z)=0$
and
$\operatorname {\mathrm {Br}}(\mathbb Z)=0$
and
([Reference MilneMil80, Chapter III, Theorem 3.9]), it follows again from the 7 term exact sequence for the Leray spectral sequence in the fppf topology for
![]() $f\colon X\rightarrow \operatorname {\mathrm {Spec}}(\mathbb Z)$
and the sheaf
$f\colon X\rightarrow \operatorname {\mathrm {Spec}}(\mathbb Z)$
and the sheaf
![]() $\mathbb {G}_{m}$
that
$\mathbb {G}_{m}$
that
The sheaf property of
![]() $R^{2}f_{*}\mathbb {G}_{m}$
again implies that
$R^{2}f_{*}\mathbb {G}_{m}$
again implies that
![]() $H^{0}_{\operatorname {\mathrm {fl}}}(\operatorname {\mathrm {Spec}}(\mathbb {Z}),R^{2}f_{*}\mathbb {G}_{m})\subseteq H^{0}_{\operatorname {\mathrm {fl}}}(\operatorname {\mathrm {Spec}}(\overline {\mathbb {Z}}),R^{2}f_{*}\mathbb {G}_{m}).$
This implies that
$H^{0}_{\operatorname {\mathrm {fl}}}(\operatorname {\mathrm {Spec}}(\mathbb {Z}),R^{2}f_{*}\mathbb {G}_{m})\subseteq H^{0}_{\operatorname {\mathrm {fl}}}(\operatorname {\mathrm {Spec}}(\overline {\mathbb {Z}}),R^{2}f_{*}\mathbb {G}_{m}).$
This implies that
Therefore, we see that
which gives the injectivity of
![]() $\operatorname {\mathrm {Br}}(X)\rightarrow \operatorname {\mathrm {Br}}(X_{\overline {\mathbb {Z}}})$
. Now we use the injectivity of
$\operatorname {\mathrm {Br}}(X)\rightarrow \operatorname {\mathrm {Br}}(X_{\overline {\mathbb {Z}}})$
. Now we use the injectivity of
![]() $\operatorname {\mathrm {Br}}(X_{\overline {\mathbb Z}}) \to \operatorname {\mathrm {Br}}(X_{\overline {\mathbb {Q}}}),$
which follows from [Reference Antieau and MeierAM20, Proposition 2.5. (iv)] after writing
$\operatorname {\mathrm {Br}}(X_{\overline {\mathbb Z}}) \to \operatorname {\mathrm {Br}}(X_{\overline {\mathbb {Q}}}),$
which follows from [Reference Antieau and MeierAM20, Proposition 2.5. (iv)] after writing
using that the stacks under consideration in the colimit are quasi-compact and quasi-separated.
Corollary 3.8. For integers
![]() $g, n \geq 0$
with
$g, n \geq 0$
with
![]() $2g-2+n> 0$
, the condition (1) in Proposition 3.5 is satisfied for
$2g-2+n> 0$
, the condition (1) in Proposition 3.5 is satisfied for
![]() $\overline {\mathcal {M}}_{g,n,\mathbb Z}.$
In particular, if
$\overline {\mathcal {M}}_{g,n,\mathbb Z}.$
In particular, if
![]() $\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{g, n, \overline {\mathbb {Q}}})=0$
, then we have
$\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{g, n, \overline {\mathbb {Q}}})=0$
, then we have
![]() $\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{g,n,\mathbb Z})=0$
.
$\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{g,n,\mathbb Z})=0$
.
Proof. By [Reference Boggi and PikaartBP00, Proposition 1.1] (cf., [Reference Fringuelli and VivianiFV23, Theorem 5.8]), we see that
![]() $\overline {\mathcal {M}}_{g,n,\overline {\mathbb {Q}}}$
is simply connected.
$\overline {\mathcal {M}}_{g,n,\overline {\mathbb {Q}}}$
is simply connected.
We shall show that
![]() $\overline {\mathcal {M}}_{g,n}(\mathbb Z)\neq \emptyset $
. We first remark that if
$\overline {\mathcal {M}}_{g,n}(\mathbb Z)\neq \emptyset $
. We first remark that if
![]() $\overline {\mathcal {M}}_{g,n}(\mathbb Z)\neq \emptyset $
, then
$\overline {\mathcal {M}}_{g,n}(\mathbb Z)\neq \emptyset $
, then
![]() $\overline {\mathcal {M}}_{g,n+1}(\mathbb Z)\neq \emptyset $
since the contraction morphisms
$\overline {\mathcal {M}}_{g,n+1}(\mathbb Z)\neq \emptyset $
since the contraction morphisms
![]() $\overline {\mathcal {M}}_{g,n+1} \to \overline {\mathcal {M}}_{g,n}$
(see [Reference KnudsenKnu83, Section 2]) have a section
$\overline {\mathcal {M}}_{g,n+1} \to \overline {\mathcal {M}}_{g,n}$
(see [Reference KnudsenKnu83, Section 2]) have a section
![]() $\overline {\mathcal {M}}_{g,n} \to \overline {\mathcal {M}}_{g,n+1}$
.
$\overline {\mathcal {M}}_{g,n} \to \overline {\mathcal {M}}_{g,n+1}$
.
To show that
![]() $\overline {\mathcal {M}}_{g,n}(\mathbb Z)\neq \emptyset $
, we proceed by induction on g. We assume that
$\overline {\mathcal {M}}_{g,n}(\mathbb Z)\neq \emptyset $
, we proceed by induction on g. We assume that
![]() $g=0$
. If
$g=0$
. If
![]() $n=3$
, the projective line
$n=3$
, the projective line
![]() $\mathbb P^1_{\mathbb Z} \to \operatorname {\mathrm {Spec}} (\mathbb Z)$
with the three sections defined by
$\mathbb P^1_{\mathbb Z} \to \operatorname {\mathrm {Spec}} (\mathbb Z)$
with the three sections defined by
![]() $0$
,
$0$
,
![]() $1$
,
$1$
,
![]() $\infty $
gives an element of
$\infty $
gives an element of
![]() $\overline {\mathcal {M}}_{0,3}(\mathbb Z)$
. By the remark in the previous paragraph, we then have
$\overline {\mathcal {M}}_{0,3}(\mathbb Z)$
. By the remark in the previous paragraph, we then have
![]() $\overline {\mathcal {M}}_{0,n}(\mathbb Z)\neq \emptyset $
for every
$\overline {\mathcal {M}}_{0,n}(\mathbb Z)\neq \emptyset $
for every
![]() $n \geq 3$
. We assume that the assertion is true for some
$n \geq 3$
. We assume that the assertion is true for some
![]() $g \geq 0$
. By using the clutching morphisms
$g \geq 0$
. By using the clutching morphisms
![]() $ \overline {\mathcal {M}}_{g,n+2} \to \overline {\mathcal {M}}_{g+1,n} $
(see [Reference KnudsenKnu83, Section 3]), and the assumption that
$ \overline {\mathcal {M}}_{g,n+2} \to \overline {\mathcal {M}}_{g+1,n} $
(see [Reference KnudsenKnu83, Section 3]), and the assumption that
![]() $\overline {\mathcal {M}}_{g,n+2}(\mathbb Z) \neq \emptyset $
, we see that
$\overline {\mathcal {M}}_{g,n+2}(\mathbb Z) \neq \emptyset $
, we see that
![]() $\overline {\mathcal {M}}_{g+1,n}(\mathbb Z)\neq \emptyset $
for any n with
$\overline {\mathcal {M}}_{g+1,n}(\mathbb Z)\neq \emptyset $
for any n with
![]() $2(g+1)-2+n> 0$
. This concludes the proof.
$2(g+1)-2+n> 0$
. This concludes the proof.
Remark 3.9. By the main results of [Reference Fringuelli and VivianiFV23], the condition (2) of Proposition 3.5 is also satisfied for
![]() $\overline {\mathcal {M}}_{g,n,\mathbb Z}$
for
$\overline {\mathcal {M}}_{g,n,\mathbb Z}$
for
![]() $g\leq 5.$
$g\leq 5.$
The following statement, together with Remark 3.9, will be needed in the proof of Theorem 1.1 for genus
![]() $3$
(see Theorem 4.14).
$3$
(see Theorem 4.14).
Lemma 3.10. Assume that we are in the situation (2) in Proposition 3.5. Let
![]() $\alpha \in \operatorname {\mathrm {Br}}(X_{\overline {\mathbb Q}})$
be an element of order n. Assume that there is a prime p such that n is not divisible by p and the image
$\alpha \in \operatorname {\mathrm {Br}}(X_{\overline {\mathbb Q}})$
be an element of order n. Assume that there is a prime p such that n is not divisible by p and the image
![]() $\alpha \vert _{X_{\overline {\mathbb {F}}_{p}}}$
of
$\alpha \vert _{X_{\overline {\mathbb {F}}_{p}}}$
of
![]() $\alpha $
under the specialization map
$\alpha $
under the specialization map
![]() $\operatorname {\mathrm {Br}}(X_{\overline {\mathbb Q}}) \to \operatorname {\mathrm {Br}}(X_{\overline {\mathbb {F}}_{p}})$
is zero. Then we have
$\operatorname {\mathrm {Br}}(X_{\overline {\mathbb Q}}) \to \operatorname {\mathrm {Br}}(X_{\overline {\mathbb {F}}_{p}})$
is zero. Then we have
![]() $\alpha =0.$
$\alpha =0.$
Proof. We consider the following diagram comparing the Kummer sequences:
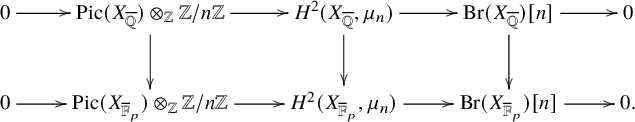
The left downward arrow is an isomorphism by (2), and the middle downward arrow is an isomorphism by base change (see the proof of [Reference Fringuelli and VivianiFV23, Proposition 7.2]). It follows that the right downward arrow is also an isomorphism. Therefore, our assumption implies that
![]() $\alpha =0.$
$\alpha =0.$
3.3 Examples
As a supplement to Proposition 3.5 (and our main result), we give a few examples here. The following claim gives a sufficient criterion for checking that
![]() $\underline {\operatorname {\mathrm {Pic}}}_{X/\mathbb Z}$
is a constant sheaf.
$\underline {\operatorname {\mathrm {Pic}}}_{X/\mathbb Z}$
is a constant sheaf.
Lemma 3.11. Let
![]() $f\colon X\rightarrow \operatorname {\mathrm {Spec}}(\mathbb Z)$
be a proper and smooth DM stack with geometrically connected fibers. We assume that
$f\colon X\rightarrow \operatorname {\mathrm {Spec}}(\mathbb Z)$
be a proper and smooth DM stack with geometrically connected fibers. We assume that
for all points
![]() $s\in \operatorname {\mathrm {Spec}}(\mathbb Z)$
. Then
$s\in \operatorname {\mathrm {Spec}}(\mathbb Z)$
. Then
![]() $\underline {\operatorname {\mathrm {Pic}}}_{X/\mathbb Z}$
is constant on a finitely generated abelian group.
$\underline {\operatorname {\mathrm {Pic}}}_{X/\mathbb Z}$
is constant on a finitely generated abelian group.
Proof. Once one knows that the sheaf
![]() $\underline {\operatorname {\mathrm {Pic}}}_{X/\mathbb Z}$
is constant, it follows that the group must be finitely generated (cf., the proof of Lemma 3.6). Consider
$\underline {\operatorname {\mathrm {Pic}}}_{X/\mathbb Z}$
is constant, it follows that the group must be finitely generated (cf., the proof of Lemma 3.6). Consider
![]() $\underline {\operatorname {\mathrm {Pic}}}^{\tau }_{X/\mathbb Z}\subset \underline {\operatorname {\mathrm {Pic}}}_{X/\mathbb Z}$
(see [Reference Fringuelli and VivianiFV23, Section 3]). By our assumptions, we know the following properties:
$\underline {\operatorname {\mathrm {Pic}}}^{\tau }_{X/\mathbb Z}\subset \underline {\operatorname {\mathrm {Pic}}}_{X/\mathbb Z}$
(see [Reference Fringuelli and VivianiFV23, Section 3]). By our assumptions, we know the following properties:
-
•
 $\underline {\operatorname {\mathrm {Pic}}}_{X/\mathbb Z}$
is étale over
$\underline {\operatorname {\mathrm {Pic}}}_{X/\mathbb Z}$
is étale over
 $\operatorname {\mathrm {Spec}}(\mathbb Z)$
.
$\operatorname {\mathrm {Spec}}(\mathbb Z)$
. -
•
 $\underline {\operatorname {\mathrm {Pic}}}^{\tau }_{X/\mathbb Z}\subset \underline {\operatorname {\mathrm {Pic}}}_{X/\mathbb Z}$
is open and closed.
$\underline {\operatorname {\mathrm {Pic}}}^{\tau }_{X/\mathbb Z}\subset \underline {\operatorname {\mathrm {Pic}}}_{X/\mathbb Z}$
is open and closed. -
•
 $\underline {\operatorname {\mathrm {Pic}}}^{\tau }_{X/\mathbb Z}$
is proper over
$\underline {\operatorname {\mathrm {Pic}}}^{\tau }_{X/\mathbb Z}$
is proper over
 $\operatorname {\mathrm {Spec}}(\mathbb Z)$
.
$\operatorname {\mathrm {Spec}}(\mathbb Z)$
.
See [Reference Fringuelli and VivianiFV23, Proposition 3.2, Theorem 3.6]. In particular, we know that
![]() $\underline {\operatorname {\mathrm {Pic}}}^{\tau }_{X/\mathbb Z}$
is finite étale over
$\underline {\operatorname {\mathrm {Pic}}}^{\tau }_{X/\mathbb Z}$
is finite étale over
![]() $\operatorname {\mathrm {Spec}}(\mathbb Z),$
so that it has to be constant by Minkowski’s theorem. We look at the exact sequence
$\operatorname {\mathrm {Spec}}(\mathbb Z),$
so that it has to be constant by Minkowski’s theorem. We look at the exact sequence
(For any geometric point
![]() $s \rightarrow \operatorname {\mathrm {Spec}}(\mathbb Z),$
the fiber
$s \rightarrow \operatorname {\mathrm {Spec}}(\mathbb Z),$
the fiber
![]() $ \operatorname {\mathrm {Num}}_{X/\mathbb Z}(s) $
is the maximal torsion free quotient of
$ \operatorname {\mathrm {Num}}_{X/\mathbb Z}(s) $
is the maximal torsion free quotient of
![]() $\operatorname {\mathrm {NS}}(X_{s})$
.) Now it suffices to show that
$\operatorname {\mathrm {NS}}(X_{s})$
.) Now it suffices to show that
![]() $\operatorname {\mathrm {Num}}_{X/\mathbb Z}$
is constant. By the same argument as [Reference Ekedahl, Hyland and Shepherd-BarronEHSB12, Proposition 4.2], we see that
$\operatorname {\mathrm {Num}}_{X/\mathbb Z}$
is constant. By the same argument as [Reference Ekedahl, Hyland and Shepherd-BarronEHSB12, Proposition 4.2], we see that
![]() $\operatorname {\mathrm {Num}}_{X/\mathbb Z}$
is locally constant, and hence constant by Minkowski’s theorem. (In loc.cit., the authors assume the projectivity of the morphism f, but the properness is enough for the argument.)
$\operatorname {\mathrm {Num}}_{X/\mathbb Z}$
is locally constant, and hence constant by Minkowski’s theorem. (In loc.cit., the authors assume the projectivity of the morphism f, but the properness is enough for the argument.)
We give an example where
![]() $X(\mathbb Z)=\emptyset ,$
but the condition (2) of Proposition 3.5 still holds, which explains why we put this condition.
$X(\mathbb Z)=\emptyset ,$
but the condition (2) of Proposition 3.5 still holds, which explains why we put this condition.
Example 3.12. Let G be a non quasi-split reductive group scheme over
![]() $\operatorname {\mathrm {Spec}}(\mathbb Z).$
Consider the scheme X of Borel subgroups of
$\operatorname {\mathrm {Spec}}(\mathbb Z).$
Consider the scheme X of Borel subgroups of
![]() $G.$
This is a projective and smooth scheme over
$G.$
This is a projective and smooth scheme over
![]() $\operatorname {\mathrm {Spec}}(\mathbb Z).$
By assumption, we have that
$\operatorname {\mathrm {Spec}}(\mathbb Z).$
By assumption, we have that
![]() $X(\mathbb Z)=\emptyset .$
However, we still have that
$X(\mathbb Z)=\emptyset .$
However, we still have that
![]() $\operatorname {\mathrm {Br}}(X)=\operatorname {\mathrm {Br}}(X_{\overline {\mathbb Q}})=0.$
In fact, since
$\operatorname {\mathrm {Br}}(X)=\operatorname {\mathrm {Br}}(X_{\overline {\mathbb Q}})=0.$
In fact, since
![]() $X_{\overline {\mathbb Q}}$
is rational, we have
$X_{\overline {\mathbb Q}}$
is rational, we have
![]() $\operatorname {\mathrm {Br}}(X_{\overline {\mathbb Q}})=0$
. By Kempf’s theorem, we have
$\operatorname {\mathrm {Br}}(X_{\overline {\mathbb Q}})=0$
. By Kempf’s theorem, we have
for any prime
![]() $p>0$
and
$p>0$
and
![]() $i> 0$
, which implies that
$i> 0$
, which implies that
![]() $\underline {\operatorname {\mathrm {Pic}}}_{X/\mathbb Z}$
is constant on a finitely generated abelian group by Lemma 3.11. This then implies via Proposition 3.5 that
$\underline {\operatorname {\mathrm {Pic}}}_{X/\mathbb Z}$
is constant on a finitely generated abelian group by Lemma 3.11. This then implies via Proposition 3.5 that
![]() $\operatorname {\mathrm {Br}}(X)=0,$
as desired.
$\operatorname {\mathrm {Br}}(X)=0,$
as desired.
We next give an easy example of a proper and smooth DM stack X over
![]() $\operatorname {\mathrm {Spec}}(\mathbb Z)$
such that
$\operatorname {\mathrm {Spec}}(\mathbb Z)$
such that
![]() $\operatorname {\mathrm {Br}}(X) \to \operatorname {\mathrm {Br}}(X_{\overline {\mathbb {Q}}})$
is not injective, in which the conditions (1) and (2) in Proposition 3.5 are not satisfied. We note that for a finite group G, the classifying stack
$\operatorname {\mathrm {Br}}(X) \to \operatorname {\mathrm {Br}}(X_{\overline {\mathbb {Q}}})$
is not injective, in which the conditions (1) and (2) in Proposition 3.5 are not satisfied. We note that for a finite group G, the classifying stack
![]() $[\operatorname {\mathrm {Spec}}(\mathbb Z)/G]$
is proper and étale over
$[\operatorname {\mathrm {Spec}}(\mathbb Z)/G]$
is proper and étale over
![]() $\operatorname {\mathrm {Spec}}(\mathbb Z)$
.
$\operatorname {\mathrm {Spec}}(\mathbb Z)$
.
Example 3.13. Consider
![]() $X=[\operatorname {\mathrm {Spec}}(\mathbb Z)/G]$
for
$X=[\operatorname {\mathrm {Spec}}(\mathbb Z)/G]$
for
![]() $G:=\mathbb Z/2\mathbb Z$
. Here, both (1) and (2) of Proposition 3.5 fail. Nevertheless, since
$G:=\mathbb Z/2\mathbb Z$
. Here, both (1) and (2) of Proposition 3.5 fail. Nevertheless, since
![]() $\operatorname {\mathrm {Pic}}(\mathbb Z)=0$
and
$\operatorname {\mathrm {Pic}}(\mathbb Z)=0$
and
![]() $\operatorname {\mathrm {Br}}(\mathbb Z)=0,$
we obtain that
$\operatorname {\mathrm {Br}}(\mathbb Z)=0,$
we obtain that
(here, the action of G on
![]() $\mathbb {G}_{m}(\mathbb Z)=\lbrace \pm 1 \rbrace $
is the trivial one). The same argument also implies that
$\mathbb {G}_{m}(\mathbb Z)=\lbrace \pm 1 \rbrace $
is the trivial one). The same argument also implies that
![]() $\operatorname {\mathrm {Br}}(X_{\overline {\mathbb {Q}}})= H^{2}(G, \mathbb {G}_{m}(\overline {\mathbb {Q}}))= 0.$
$\operatorname {\mathrm {Br}}(X_{\overline {\mathbb {Q}}})= H^{2}(G, \mathbb {G}_{m}(\overline {\mathbb {Q}}))= 0.$
Finally, let us include the following example, which shows our vanishing result (Theorem 1.1) does not hold for proper and smooth DM stacks over
![]() $\operatorname {\mathrm {Spec}} (\mathbb Z)$
in general.
$\operatorname {\mathrm {Spec}} (\mathbb Z)$
in general.
Example 3.14. Consider
![]() $X=[\operatorname {\mathrm {Spec}}(\mathbb Z)/S_{4}],$
where
$X=[\operatorname {\mathrm {Spec}}(\mathbb Z)/S_{4}],$
where
![]() $S_{4}$
is the symmetric group on
$S_{4}$
is the symmetric group on
![]() $4$
elements. By the same argument as in Example 3.13, we have
$4$
elements. By the same argument as in Example 3.13, we have
4 Brauer groups of moduli stacks of stable curves
In this section, we prove our vanishing results when working over
![]() $\overline {\mathbb {Q}}.$
Recall that the case where
$\overline {\mathbb {Q}}.$
Recall that the case where
![]() $g=0$
is easy to prove; see Remark 1.3. So it is enough to consider the case where
$g=0$
is easy to prove; see Remark 1.3. So it is enough to consider the case where
![]() $g \geq 1$
.
$g \geq 1$
.
4.1 Genus one
The next proposition is easy to prove because one has a very good handle on the geometry of
![]() $\mathcal {M}_{1,1,\mathbb {C}}$
.
$\mathcal {M}_{1,1,\mathbb {C}}$
.
Proposition 4.1.
![]() $\operatorname {\mathrm {Br}}(\mathcal {M}_{1,1,\overline {\mathbb {Q}}})=0;$
in particular, we have that
$\operatorname {\mathrm {Br}}(\mathcal {M}_{1,1,\overline {\mathbb {Q}}})=0;$
in particular, we have that
![]() $\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{1,1,\overline {\mathbb {Q}}})=0.$
$\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{1,1,\overline {\mathbb {Q}}})=0.$
Proof. This is proved in [Reference Antieau and MeierAM20, Theorem 1.1 (1)]. Here, we give an independent argument: we first claim that
By comparing the two short exact sequences
and
induced by Kummer exact sequences, and using invariance of étale cohomology with torsion coefficients under choice of algebraically closed base field (cf., proof of Lemma 2.7), this boils down to showing that
![]() $\operatorname {\mathrm {Pic}}(\mathcal {M}_{1,1,\overline {\mathbb {Q}}})/\ell ^{n}\simeq \operatorname {\mathrm {Pic}}(\mathcal {M}_{1,1,\mathbb {C}})/\ell ^{n}$
. This follows from [Reference Fulton and OlssonFO10]. In fact, in loc.cit., it is proved that
$\operatorname {\mathrm {Pic}}(\mathcal {M}_{1,1,\overline {\mathbb {Q}}})/\ell ^{n}\simeq \operatorname {\mathrm {Pic}}(\mathcal {M}_{1,1,\mathbb {C}})/\ell ^{n}$
. This follows from [Reference Fulton and OlssonFO10]. In fact, in loc.cit., it is proved that
Repeating this argument, but now using as an input the string of identifications
![]() $\operatorname {\mathrm {Pic}}(\mathcal {M}^{\operatorname {\mathrm {an}}}_{1,1,\mathbb {C}})\simeq \operatorname {\mathrm {Pic}}(\mathcal {M}_{1,1,\mathbb {C}})\simeq \mathbb {Z}/12\mathbb Z$
(see [Reference Arbarello and CornalbaAC87]) and étale-Betti comparison for DM stacks, we see that
$\operatorname {\mathrm {Pic}}(\mathcal {M}^{\operatorname {\mathrm {an}}}_{1,1,\mathbb {C}})\simeq \operatorname {\mathrm {Pic}}(\mathcal {M}_{1,1,\mathbb {C}})\simeq \mathbb {Z}/12\mathbb Z$
(see [Reference Arbarello and CornalbaAC87]) and étale-Betti comparison for DM stacks, we see that
Here,
![]() $\operatorname {\mathrm {Br}}(\mathcal {M}^{\operatorname {\mathrm {an}}}_{1,1,\mathbb {C}}):=H^2(\mathcal {M}^{\operatorname {\mathrm {an}}}_{1,1,\mathbb {C}}, \mathbb {G}_m)_{\operatorname {\mathrm {tors}}}$
.
$\operatorname {\mathrm {Br}}(\mathcal {M}^{\operatorname {\mathrm {an}}}_{1,1,\mathbb {C}}):=H^2(\mathcal {M}^{\operatorname {\mathrm {an}}}_{1,1,\mathbb {C}}, \mathbb {G}_m)_{\operatorname {\mathrm {tors}}}$
.
Thus, it suffices to show that
![]() $\operatorname {\mathrm {Br}}(\mathcal {M}^{\operatorname {\mathrm {an}}}_{1,1,\mathbb {C}})=0$
. Observe that it then suffices to show that
$\operatorname {\mathrm {Br}}(\mathcal {M}^{\operatorname {\mathrm {an}}}_{1,1,\mathbb {C}})=0$
. Observe that it then suffices to show that
But
using that
![]() $\operatorname {\mathrm {SL}}_{2}(\mathbb Z)=\mathbb Z/4\mathbb Z \ast _{\mathbb Z/2\mathbb Z} \mathbb Z/6\mathbb Z$
(use [Reference BrownBro82, Corollary 7.7]).
$\operatorname {\mathrm {SL}}_{2}(\mathbb Z)=\mathbb Z/4\mathbb Z \ast _{\mathbb Z/2\mathbb Z} \mathbb Z/6\mathbb Z$
(use [Reference BrownBro82, Corollary 7.7]).
The cases
![]() $(g,n)=(1,n)$
for
$(g,n)=(1,n)$
for
![]() $2\leq n \leq 6$
lie deeper and require very recent work of Battistella-Di Lorenzo [Reference Battistella and LorenzoBL24] (who compute the integral Chow ring in the cases
$2\leq n \leq 6$
lie deeper and require very recent work of Battistella-Di Lorenzo [Reference Battistella and LorenzoBL24] (who compute the integral Chow ring in the cases
![]() $(1,3)$
and
$(1,3)$
and
![]() $(1,4)$
).
$(1,4)$
).
Proposition 4.2.
![]() $\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{1,n,\overline {\mathbb {Q}}})=0$
for
$\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{1,n,\overline {\mathbb {Q}}})=0$
for
![]() $2\leq n \leq 6.$
$2\leq n \leq 6.$
Proof. If not specified, all stacks in this proof will be over
![]() $\overline {\mathbb {Q}}.$
(In fact, the following argument also gives another proof of the equality
$\overline {\mathbb {Q}}.$
(In fact, the following argument also gives another proof of the equality
![]() $\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{1,1,\overline {\mathbb {Q}}})=0$
.)
$\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{1,1,\overline {\mathbb {Q}}})=0$
.)
By [Reference Ranganathan, Santos-Parker and WiseRSPW19], [Reference SmythSmy19] (see also the introduction to [Reference Battistella and LorenzoBL24]), we have a diagram
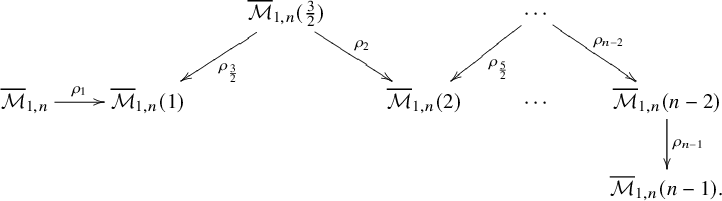
We know the following:
-
• By [Reference Battistella and LorenzoBL24, Theorem 1.12], we have for
 $m\leq 5,$
that the morphisms
$m\leq 5,$
that the morphisms
 $\rho _{m}$
are weighted blow-ups (see [Reference Battistella and LorenzoBL24, Definition 1.1]) in loci which are of codimension greater or equal than
$\rho _{m}$
are weighted blow-ups (see [Reference Battistella and LorenzoBL24, Definition 1.1]) in loci which are of codimension greater or equal than
 $2.$
$2.$
-
• The morphisms
 $\rho _{\frac {j}{2}}$
are ordinary blow-ups (this is by construction).
$\rho _{\frac {j}{2}}$
are ordinary blow-ups (this is by construction). -
• By [Reference Battistella and LorenzoBL24, Theorem 1.5], the stacks
 $\overline {\mathcal {M}}_{1,n}(m)$
are smooth for
$\overline {\mathcal {M}}_{1,n}(m)$
are smooth for
 $m\leq 5.$
Observe that this also implies (via Lemma 2.1) that the stacks
$m\leq 5.$
Observe that this also implies (via Lemma 2.1) that the stacks
 $\overline {\mathcal {M}}_{1,n}(\frac {j}{2})$
are smooth.
$\overline {\mathcal {M}}_{1,n}(\frac {j}{2})$
are smooth. -
• For
 $2\leq n \leq 6,$
we have that
$2\leq n \leq 6,$
we have that
 $\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{1,n}(n-1))=0.$
Namely, for
$\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{1,n}(n-1))=0.$
Namely, for
 $2\leq n \leq 5,$
this follows from [Reference Battistella and LorenzoBL24, Proposition 1.8], which identifies
$2\leq n \leq 5,$
this follows from [Reference Battistella and LorenzoBL24, Proposition 1.8], which identifies
 $\overline {\mathcal {M}}_{1,n}(n-1)$
as weighted projective spaces
$\overline {\mathcal {M}}_{1,n}(n-1)$
as weighted projective spaces
 $\mathcal {P}(a_{1},\ldots ,a_{n+1})$
for certain explicit values of
$\mathcal {P}(a_{1},\ldots ,a_{n+1})$
for certain explicit values of
 $a_{i}$
for
$a_{i}$
for
 $2\leq n \leq 4$
and as
$2\leq n \leq 4$
and as
 $\mathbb {P}^{5}$
for
$\mathbb {P}^{5}$
for
 $n=5,$
together with [Reference ShinShi23, Theorem 1.2], which implies that
$n=5,$
together with [Reference ShinShi23, Theorem 1.2], which implies that
 $\operatorname {\mathrm {Br}}(\mathcal {P}(a_{1},\ldots ,a_{k}))=0.$
For
$\operatorname {\mathrm {Br}}(\mathcal {P}(a_{1},\ldots ,a_{k}))=0.$
For
 $n=6,$
we use [Reference Lekili and PolishchukLP19, Corollary 1.5.5, Proposition 1.7.1], together with
$n=6,$
we use [Reference Lekili and PolishchukLP19, Corollary 1.5.5, Proposition 1.7.1], together with  $$ \begin{align*}\operatorname{\mathrm{Br}}(\text{Gr}(k,m))=0. \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Br}}(\text{Gr}(k,m))=0. \end{align*} $$
-
• By [Reference Quek and RydhQD22, Remark 3.2.10], a weighted blow-up is an isomorphism away from the blow-up center.
Finally, observe that all entries in the above diagram are irreducible as DM stacks, so that we may apply Corollary 2.3 step-by-step to deduce the desired vanishing.
4.2 Genus two
Next, we quickly explain why the case
![]() $g=2$
is already contained in the literature:
$g=2$
is already contained in the literature:
Proposition 4.3 (Di Lorenzo-Pirisi).
The equality
![]() $ \operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{2,\overline {\mathbb {Q}}})=0 $
holds.
$ \operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{2,\overline {\mathbb {Q}}})=0 $
holds.
Proof. This result is contained in [Reference Di Lorenzo and PirisiDLP21, Theorem A.1]. Although this is probably trivial for the experts, let us explain why. Let
![]() $\mathcal {H}_{g,\overline {\mathbb {Q}}}$
be the moduli stack over
$\mathcal {H}_{g,\overline {\mathbb {Q}}}$
be the moduli stack over
![]() $\overline {\mathbb {Q}}$
of hyper-elliptic curves of genus g (in the sense of [Reference Arsie and VistoliAV04]; that is, a genus g hyper-elliptic curve over a scheme S consists of
$\overline {\mathbb {Q}}$
of hyper-elliptic curves of genus g (in the sense of [Reference Arsie and VistoliAV04]; that is, a genus g hyper-elliptic curve over a scheme S consists of
![]() $X\rightarrow P \rightarrow S,$
where
$X\rightarrow P \rightarrow S,$
where
![]() $X\rightarrow S$
is a proper and smooth morphism with all geometric fibers connected curves of genus g,
$X\rightarrow S$
is a proper and smooth morphism with all geometric fibers connected curves of genus g,
![]() $X\rightarrow P$
is a morphism of schemes which is finite, fppf and of degree
$X\rightarrow P$
is a morphism of schemes which is finite, fppf and of degree
![]() $2$
and
$2$
and
![]() $P\rightarrow S$
is a family of genus
$P\rightarrow S$
is a family of genus
![]() $0$
curves). This is an irreducible smooth algebraic stack over
$0$
curves). This is an irreducible smooth algebraic stack over
![]() $\overline {\mathbb {Q}}$
of dimension
$\overline {\mathbb {Q}}$
of dimension
![]() $2g-1,$
as proven in [Reference Arsie and VistoliAV04]. For
$2g-1,$
as proven in [Reference Arsie and VistoliAV04]. For
![]() $g\geq 2$
, the morphism
$g\geq 2$
, the morphism
![]() $ \mathcal {H}_{g,\overline {\mathbb {Q}}}\rightarrow \mathcal {M}_{g,\overline {\mathbb {Q}}} $
that forgets P is a closed immersion. For
$ \mathcal {H}_{g,\overline {\mathbb {Q}}}\rightarrow \mathcal {M}_{g,\overline {\mathbb {Q}}} $
that forgets P is a closed immersion. For
![]() $g=2,$
it follows that
$g=2,$
it follows that
since
![]() $\mathrm {dim} (\mathcal {H}_{2,\overline {\mathbb {Q}}})=\mathrm {dim} (\mathcal {M}_{2,\overline {\mathbb {Q}}})=3$
. The stack of stable hyper-elliptic genus g curves
$\mathrm {dim} (\mathcal {H}_{2,\overline {\mathbb {Q}}})=\mathrm {dim} (\mathcal {M}_{2,\overline {\mathbb {Q}}})=3$
. The stack of stable hyper-elliptic genus g curves
![]() $\overline {\mathcal {H}}_{g,\overline {\mathbb {Q}}}$
is identified with the closure of
$\overline {\mathcal {H}}_{g,\overline {\mathbb {Q}}}$
is identified with the closure of
![]() $\mathcal {H}_{g,\overline {\mathbb {Q}}}$
inside of
$\mathcal {H}_{g,\overline {\mathbb {Q}}}$
inside of
![]() $\overline {\mathcal {M}}_{g,\overline {\mathbb {Q}}}.$
It follows that
$\overline {\mathcal {M}}_{g,\overline {\mathbb {Q}}}.$
It follows that
But the mentioned result of Di Lorenzo-Pirisi implies that
![]() $ \operatorname {\mathrm {Br}}(\overline {\mathcal {H}}_{2,\overline {\mathbb {Q}}})=0. $
$ \operatorname {\mathrm {Br}}(\overline {\mathcal {H}}_{2,\overline {\mathbb {Q}}})=0. $
4.3 Genus three
The purpose of this subsection is to prove that
![]() $\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{3, \overline {\mathbb Q}})=0$
; see Theorem 4.14. For this, we first recall some results from [Reference Lorenzo and PirisiLP24].
$\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{3, \overline {\mathbb Q}})=0$
; see Theorem 4.14. For this, we first recall some results from [Reference Lorenzo and PirisiLP24].
It is shown in [Reference Lorenzo and PirisiLP24] that for a field k of characteristic
![]() $p \geq 3$
, there is a natural isomorphism
$p \geq 3$
, there is a natural isomorphism
where
![]() $B_p$
is a p-primary torsion group, while for
$B_p$
is a p-primary torsion group, while for
![]() $\text {char}(k)=0,$
we have
$\text {char}(k)=0,$
we have
We denote the generator of
![]() $\mathbb Z/2\mathbb Z \subset \operatorname {\mathrm {Br}}(\mathcal {M}_{3, k})$
by
$\mathbb Z/2\mathbb Z \subset \operatorname {\mathrm {Br}}(\mathcal {M}_{3, k})$
by
![]() $\gamma $
. This generator
$\gamma $
. This generator
![]() $\gamma $
is constructed explicitly in [Reference Lorenzo and PirisiLP24]. Let C be a projective smooth curve over k of genus
$\gamma $
is constructed explicitly in [Reference Lorenzo and PirisiLP24]. Let C be a projective smooth curve over k of genus
![]() $3$
. Let
$3$
. Let
![]() $\gamma (C) \in \operatorname {\mathrm {Br}}(k)[2]$
be the element obtained by pulling back
$\gamma (C) \in \operatorname {\mathrm {Br}}(k)[2]$
be the element obtained by pulling back
![]() $\gamma \in \operatorname {\mathrm {Br}}(\mathcal {M}_{3, k})$
along the morphism
$\gamma \in \operatorname {\mathrm {Br}}(\mathcal {M}_{3, k})$
along the morphism
![]() $\operatorname {\mathrm {Spec}} (k) \to \mathcal {M}_{3, k}$
corresponding to C. We shall recall the description of
$\operatorname {\mathrm {Spec}} (k) \to \mathcal {M}_{3, k}$
corresponding to C. We shall recall the description of
![]() $\gamma (C)$
in a special case which will be needed for our purposes.
$\gamma (C)$
in a special case which will be needed for our purposes.
Example 4.4. Let
![]() $X \subset \mathbb P^3_k$
be a smooth cubic surface over k. It is well known that
$X \subset \mathbb P^3_k$
be a smooth cubic surface over k. It is well known that
![]() $X_{\overline {k}}$
contains exactly
$X_{\overline {k}}$
contains exactly
![]() $27$
lines. Since the absolute Galois group of k acts on the set of lines in
$27$
lines. Since the absolute Galois group of k acts on the set of lines in
![]() $X_{\overline {k}}$
, we obtain the associated étale algebra
$X_{\overline {k}}$
, we obtain the associated étale algebra
![]() $E_X$
over k of degree
$E_X$
over k of degree
![]() $27$
. Let
$27$
. Let
![]() $P \in X(k)$
be a k-rational point which is not contained in any line in
$P \in X(k)$
be a k-rational point which is not contained in any line in
![]() $X_{\overline {k}}$
and let
$X_{\overline {k}}$
and let
![]() $H \subset \mathbb P^3_k$
be a hyperplane such that P is not contained in H. Then we have a morphism
$H \subset \mathbb P^3_k$
be a hyperplane such that P is not contained in H. Then we have a morphism
induced by the projection onto H. This morphism expresses
![]() $\mathrm {Bl}_P (X)$
as a double covering of H whose ramification locus is a smooth quartic curve
$\mathrm {Bl}_P (X)$
as a double covering of H whose ramification locus is a smooth quartic curve
![]() $C \subset H$
over k. Then
$C \subset H$
over k. Then
agrees with the second Galois-Stiefel-Whitney class
![]() $\alpha _2(E_X)$
as explained in [Reference Lorenzo and PirisiLP24, Section 3.4, Section 3.5]. We recall that
$\alpha _2(E_X)$
as explained in [Reference Lorenzo and PirisiLP24, Section 3.4, Section 3.5]. We recall that
![]() $\alpha _2(E_X)$
is the degree
$\alpha _2(E_X)$
is the degree
![]() $2$
term of the total Galois-Stiefel-Whitney class
$2$
term of the total Galois-Stiefel-Whitney class
![]() $\alpha _{\mathrm {tot}}(E_X)$
; see [Reference Lorenzo and PirisiLP24, Section 3.3] for the definition. Strictly speaking, the second Galois-Stiefel-Whitney class
$\alpha _{\mathrm {tot}}(E_X)$
; see [Reference Lorenzo and PirisiLP24, Section 3.3] for the definition. Strictly speaking, the second Galois-Stiefel-Whitney class
![]() $\alpha _2(E_X)$
is an element of
$\alpha _2(E_X)$
is an element of
![]() $H^2_{\operatorname {\acute {e}t}}(\operatorname {\mathrm {Spec}} (k), \mu ^{\otimes 2}_2)$
. However, since
$H^2_{\operatorname {\acute {e}t}}(\operatorname {\mathrm {Spec}} (k), \mu ^{\otimes 2}_2)$
. However, since
![]() $\mu _2$
can be naturally identified with
$\mu _2$
can be naturally identified with
![]() $\mathbb Z/2\mathbb Z$
, we may regard
$\mathbb Z/2\mathbb Z$
, we may regard
![]() $\alpha _2(E_X)$
as an element of
$\alpha _2(E_X)$
as an element of
![]() $H^2_{\operatorname {\acute {e}t}}(\operatorname {\mathrm {Spec}} (k), \mu _2)$
.
$H^2_{\operatorname {\acute {e}t}}(\operatorname {\mathrm {Spec}} (k), \mu _2)$
.
Let p be a prime such that
![]() $p \geq 11$
. Let
$p \geq 11$
. Let
![]() $\mathbb F_q$
be a finite field with
$\mathbb F_q$
be a finite field with
![]() $q=p^r$
elements. We consider a local field
$q=p^r$
elements. We consider a local field
![]() $F=\mathbb F_q((t))$
. In the following Example 4.5 (resp. Example 4.6), we will give an example of a smooth quartic curve C over F such that
$F=\mathbb F_q((t))$
. In the following Example 4.5 (resp. Example 4.6), we will give an example of a smooth quartic curve C over F such that
![]() $\gamma (C) \in \operatorname {\mathrm {Br}}(F)[2]$
is not zero when
$\gamma (C) \in \operatorname {\mathrm {Br}}(F)[2]$
is not zero when
![]() $(q-1)/2$
is even (resp. odd).
$(q-1)/2$
is even (resp. odd).
Let
![]() $E_1:=F(\sqrt {t})$
, which is a totally ramified extension of F of degree
$E_1:=F(\sqrt {t})$
, which is a totally ramified extension of F of degree
![]() $2$
. Let
$2$
. Let
![]() $u \in \mathbb F_q^\times $
be an element such that
$u \in \mathbb F_q^\times $
be an element such that
![]() $\sqrt {u}$
is not contained in
$\sqrt {u}$
is not contained in
![]() $\mathbb F_q$
and let
$\mathbb F_q$
and let
![]() $E_2:=F(\sqrt {u})$
. Then
$E_2:=F(\sqrt {u})$
. Then
![]() $E_2$
is an unramified extension of F of degree
$E_2$
is an unramified extension of F of degree
![]() $2$
. Let
$2$
. Let
![]() $K:=F(\sqrt {t}, \sqrt {u})$
.
$K:=F(\sqrt {t}, \sqrt {u})$
.
Example 4.5. We set
 $$ \begin{align*} &u_1:= 1 + \sqrt{t}, &u_2 &:= 1 - \sqrt{t}, \\ &u_3:= 1 + \sqrt{u}, &u_4 &:= 1 - \sqrt{u}, \\ &u_5:= 2 + t, &u_6 &:= t. \end{align*} $$
$$ \begin{align*} &u_1:= 1 + \sqrt{t}, &u_2 &:= 1 - \sqrt{t}, \\ &u_3:= 1 + \sqrt{u}, &u_4 &:= 1 - \sqrt{u}, \\ &u_5:= 2 + t, &u_6 &:= t. \end{align*} $$
One can check that they satisfy the conditions
 $$\begin{align*}u_i \neq u_j \, \, (i \neq j), \quad u_i+u_j+u_k \neq 0 \, \, (i, j, k \text{ are distinct}), \quad \sum^6_{i=1} u_i \neq 0, \end{align*}$$
$$\begin{align*}u_i \neq u_j \, \, (i \neq j), \quad u_i+u_j+u_k \neq 0 \, \, (i, j, k \text{ are distinct}), \quad \sum^6_{i=1} u_i \neq 0, \end{align*}$$
or equivalently, the
![]() $6$
points
$6$
points
![]() $U_i:=[u^{-2}_i, u^{-3}_i, 1] \in \mathbb P^2_{K}$
are in a general position (i.e., they are not on a conic and no three of
$U_i:=[u^{-2}_i, u^{-3}_i, 1] \in \mathbb P^2_{K}$
are in a general position (i.e., they are not on a conic and no three of
![]() $u_i$
lie on a line). Since
$u_i$
lie on a line). Since
![]() $u_1$
is conjugate to
$u_1$
is conjugate to
![]() $u_2$
, the points
$u_2$
, the points
![]() $U_1$
and
$U_1$
and
![]() $U_2$
descend to a closed point
$U_2$
descend to a closed point
![]() $U_{12} \colon \operatorname {\mathrm {Spec}} (E_1) \hookrightarrow \mathbb P^2_{F}$
by Galois descent. Similarly,
$U_{12} \colon \operatorname {\mathrm {Spec}} (E_1) \hookrightarrow \mathbb P^2_{F}$
by Galois descent. Similarly,
![]() $U_3$
and
$U_3$
and
![]() $U_4$
descend to a closed point
$U_4$
descend to a closed point
![]() $U_{34} \colon \operatorname {\mathrm {Spec}} (E_2) \hookrightarrow \mathbb P^2_{F}$
. Then the blow-up X of
$U_{34} \colon \operatorname {\mathrm {Spec}} (E_2) \hookrightarrow \mathbb P^2_{F}$
. Then the blow-up X of
![]() $\mathbb P^2_{F}$
along the closed points
$\mathbb P^2_{F}$
along the closed points
![]() $U_{12}$
,
$U_{12}$
,
![]() $U_{34}$
,
$U_{34}$
,
![]() $U_5$
,
$U_5$
,
![]() $U_6$
is naturally a smooth cubic surface
$U_6$
is naturally a smooth cubic surface
![]() $X \hookrightarrow \mathbb P^3_{F}$
over F. By the same argument as in [Reference Lorenzo and PirisiLP24, Section 3.4], we can check that
$X \hookrightarrow \mathbb P^3_{F}$
over F. By the same argument as in [Reference Lorenzo and PirisiLP24, Section 3.4], we can check that
We note that
![]() $\alpha _{\mathrm {tot}}(F)= 1$
. We have
$\alpha _{\mathrm {tot}}(F)= 1$
. We have
![]() $\alpha _{\mathrm {tot}}(E_1)= 1 + \{ t \}$
and
$\alpha _{\mathrm {tot}}(E_1)= 1 + \{ t \}$
and
![]() $\alpha _{\mathrm {tot}}(E_2)= 1 + \{ u \}$
. We have
$\alpha _{\mathrm {tot}}(E_2)= 1 + \{ u \}$
. We have
![]() $\alpha _1(K) = 0$
and
$\alpha _1(K) = 0$
and
![]() $\alpha _2(K) = \{ t, u \} + \{ -1, tu \}$
by the same computation as in [Reference Lorenzo and PirisiLP24, Example 3.11]. Using the multiplicativity of the total Galois-Stiefel-Whitney classes, we obtain
$\alpha _2(K) = \{ t, u \} + \{ -1, tu \}$
by the same computation as in [Reference Lorenzo and PirisiLP24, Example 3.11]. Using the multiplicativity of the total Galois-Stiefel-Whitney classes, we obtain
![]() $\alpha _2(E_X) = \alpha _2(K) = \{ t, u \} + \{ -1, tu \}$
.
$\alpha _2(E_X) = \alpha _2(K) = \{ t, u \} + \{ -1, tu \}$
.
We have
![]() $\operatorname {\mathrm {Br}}(F)[2] \simeq \mathbb Z/2\mathbb Z $
by local class field theory. We further identify
$\operatorname {\mathrm {Br}}(F)[2] \simeq \mathbb Z/2\mathbb Z $
by local class field theory. We further identify
![]() $\mathbb Z/2\mathbb Z$
with
$\mathbb Z/2\mathbb Z$
with
![]() $\mu _2(F)= \{-1, 1 \}$
. Under these identifications,
$\mu _2(F)= \{-1, 1 \}$
. Under these identifications,
![]() $\{ t, u \}$
agrees with the Hilbert symbol
$\{ t, u \}$
agrees with the Hilbert symbol
![]() $(t, u)$
on F. By [Reference SerreSer79, Chapter XIV, Section 3, Corollary], we then have
$(t, u)$
on F. By [Reference SerreSer79, Chapter XIV, Section 3, Corollary], we then have
![]() $\{ t, u \} = u^{(q-1)/2}$
. Similarly, we get
$\{ t, u \} = u^{(q-1)/2}$
. Similarly, we get
![]() $\{ -1, tu \} = (-1)^{(q-1)/2}$
. Since
$\{ -1, tu \} = (-1)^{(q-1)/2}$
. Since
![]() $\sqrt {u}$
is not contained in
$\sqrt {u}$
is not contained in
![]() $\mathbb F_q$
, we see that
$\mathbb F_q$
, we see that
![]() $\{ t, u \} = u^{(q-1)/2} =-1$
. It follows that
$\{ t, u \} = u^{(q-1)/2} =-1$
. It follows that
Therefore, for a smooth quartic curve
![]() $C \subset \mathbb P^2_{F}$
over F obtained in the same way as in Example 4.4, we have
$C \subset \mathbb P^2_{F}$
over F obtained in the same way as in Example 4.4, we have
Example 4.6. We set
 $$ \begin{align*} &u_1:= 1 + \sqrt{t}, &u_2 &:= 1 - \sqrt{t}, \\ &u_3:= 1 + \sqrt{u}, &u_4 &:= 1 - \sqrt{u}, \\ &u_5:= 1 + t + 2\sqrt{u}, &u_6 &:= 1 + t - 2\sqrt{u}. \end{align*} $$
$$ \begin{align*} &u_1:= 1 + \sqrt{t}, &u_2 &:= 1 - \sqrt{t}, \\ &u_3:= 1 + \sqrt{u}, &u_4 &:= 1 - \sqrt{u}, \\ &u_5:= 1 + t + 2\sqrt{u}, &u_6 &:= 1 + t - 2\sqrt{u}. \end{align*} $$
The
![]() $6$
points
$6$
points
![]() $U_i:=[u^{-2}_i, u^{-3}_i, 1] \in \mathbb P^2_{K}$
are in a general position. Since
$U_i:=[u^{-2}_i, u^{-3}_i, 1] \in \mathbb P^2_{K}$
are in a general position. Since
![]() $u_1$
is conjugate to
$u_1$
is conjugate to
![]() $u_2$
,
$u_2$
,
![]() $U_1$
and
$U_1$
and
![]() $U_2$
descend to a closed point
$U_2$
descend to a closed point
![]() $U_{12} \colon \operatorname {\mathrm {Spec}} (E_1) \hookrightarrow \mathbb P^2_{F}$
. Similarly,
$U_{12} \colon \operatorname {\mathrm {Spec}} (E_1) \hookrightarrow \mathbb P^2_{F}$
. Similarly,
![]() $U_3$
and
$U_3$
and
![]() $U_4$
descend to a closed point
$U_4$
descend to a closed point
![]() $U_{34} \colon \operatorname {\mathrm {Spec}} (E_2) \hookrightarrow \mathbb P^2_{F}$
, and
$U_{34} \colon \operatorname {\mathrm {Spec}} (E_2) \hookrightarrow \mathbb P^2_{F}$
, and
![]() $U_5$
and
$U_5$
and
![]() $U_6$
descend to a closed point
$U_6$
descend to a closed point
![]() $U_{56} \colon \operatorname {\mathrm {Spec}} (E_2) \hookrightarrow \mathbb P^2_{F}$
.
$U_{56} \colon \operatorname {\mathrm {Spec}} (E_2) \hookrightarrow \mathbb P^2_{F}$
.
Then the blow-up X of
![]() $\mathbb P^2_{F}$
along the closed points
$\mathbb P^2_{F}$
along the closed points
![]() $U_{12}$
,
$U_{12}$
,
![]() $U_{34}$
,
$U_{34}$
,
![]() $U_{56}$
is naturally a smooth cubic surface
$U_{56}$
is naturally a smooth cubic surface
![]() $X \hookrightarrow \mathbb P^3_{F}$
over F. By the same argument as in [Reference Lorenzo and PirisiLP24, Section 3.4], we can check that
$X \hookrightarrow \mathbb P^3_{F}$
over F. By the same argument as in [Reference Lorenzo and PirisiLP24, Section 3.4], we can check that
We note that
![]() $\alpha _{\mathrm {tot}}(F)= 1$
. We have
$\alpha _{\mathrm {tot}}(F)= 1$
. We have
![]() $\alpha _{\mathrm {tot}}(E_1)= 1 + \{ t \}$
and
$\alpha _{\mathrm {tot}}(E_1)= 1 + \{ t \}$
and
![]() $\alpha _{\mathrm {tot}}(E_2)= 1 + \{ u \}$
. It follows that
$\alpha _{\mathrm {tot}}(E_2)= 1 + \{ u \}$
. It follows that
![]() $ \alpha _{\mathrm {tot}}(E^2_1) = 1 + \{ t, t \} $
and
$ \alpha _{\mathrm {tot}}(E^2_1) = 1 + \{ t, t \} $
and
where
![]() $\beta $
is some element of degree
$\beta $
is some element of degree
![]() $\geq 3$
. We have
$\geq 3$
. We have
![]() $\alpha _1(K) = 0$
and
$\alpha _1(K) = 0$
and
![]() $\alpha _2(K) = \{ t, u \} + \{ -1, tu \}$
by the same computation as in [Reference Lorenzo and PirisiLP24, Example 3.11]. In particular, we obtain
$\alpha _2(K) = \{ t, u \} + \{ -1, tu \}$
by the same computation as in [Reference Lorenzo and PirisiLP24, Example 3.11]. In particular, we obtain
for some element
![]() $\beta '$
of degree
$\beta '$
of degree
![]() $\geq 3$
. Using the multiplicativity of the total Galois-Stiefel-Whitney classes, we obtain
$\geq 3$
. Using the multiplicativity of the total Galois-Stiefel-Whitney classes, we obtain
As in the previous example, by [Reference SerreSer79, Chapter XIV, Section 3, Corollary], we have
![]() $\{ t, t \} = (-1)^{(q-1)/2}$
and
$\{ t, t \} = (-1)^{(q-1)/2}$
and
![]() $\{ u, u \} = 1$
. It follows that
$\{ u, u \} = 1$
. It follows that
Therefore, for a smooth quartic curve
![]() $C \subset \mathbb P^2_{F}$
over F obtained in the same way as in Example 4.4, we have
$C \subset \mathbb P^2_{F}$
over F obtained in the same way as in Example 4.4, we have
Our next task is to show that smooth quartic curves C over F from the previous examples can be taken to have stable reduction over
![]() $\mathcal {O}_F=\mathbb F_q[[t]]$
(without enlarging F). We let
$\mathcal {O}_F=\mathbb F_q[[t]]$
(without enlarging F). We let
![]() $u_1, \dotsc , u_6$
be as in Example 4.5 when
$u_1, \dotsc , u_6$
be as in Example 4.5 when
![]() $(q-1)/2$
is even, and let
$(q-1)/2$
is even, and let
![]() $u_1, \dotsc , u_6$
be as in Example 4.6 when
$u_1, \dotsc , u_6$
be as in Example 4.6 when
![]() $(q-1)/2$
is odd. We keep the notation of the previous examples. By the result of Shioda [Reference ShiodaShi95, Theorem 14], we know the defining equation of
$(q-1)/2$
is odd. We keep the notation of the previous examples. By the result of Shioda [Reference ShiodaShi95, Theorem 14], we know the defining equation of
![]() $X \hookrightarrow \mathbb P^3_{F}$
. We shall recall his result.
$X \hookrightarrow \mathbb P^3_{F}$
. We shall recall his result.
Proposition 4.7 [Reference ShiodaShi95, Theorem 14].
We set
Let
![]() $\varepsilon _m$
be the m-th elementary symmetric function of the
$\varepsilon _m$
be the m-th elementary symmetric function of the
![]() $27$
elements in K
$27$
elements in K
We set
 $$ \begin{align*} p_2&:= \varepsilon_2/12, \\ p_1&:= \varepsilon_5/48, \\ q_2&:= (\varepsilon_6-168p^3_2)/96, \\ p_0&:= (\varepsilon_8-294 p^4_2-528 p_2 q_2)/480, \\ q_1&:= (\varepsilon_9 - 1008 p_1 p^2_2)/1344, \\ q_0&:= (\varepsilon_{12}-608 p^2_1 p_2-4768 p_0 p^2_2-252 p^6_2-1200 p^3_2 q_2+1248 q^2_2)/17280, \end{align*} $$
$$ \begin{align*} p_2&:= \varepsilon_2/12, \\ p_1&:= \varepsilon_5/48, \\ q_2&:= (\varepsilon_6-168p^3_2)/96, \\ p_0&:= (\varepsilon_8-294 p^4_2-528 p_2 q_2)/480, \\ q_1&:= (\varepsilon_9 - 1008 p_1 p^2_2)/1344, \\ q_0&:= (\varepsilon_{12}-608 p^2_1 p_2-4768 p_0 p^2_2-252 p^6_2-1200 p^3_2 q_2+1248 q^2_2)/17280, \end{align*} $$
which make sense since
![]() $p \geq 11$
. (These elements belong to F, and in fact belong to
$p \geq 11$
. (These elements belong to F, and in fact belong to
![]() $\mathcal {O}_F$
.) Then, the smooth cubic surface
$\mathcal {O}_F$
.) Then, the smooth cubic surface
![]() $X \hookrightarrow \mathbb P^3_{F}= \operatorname {\mathrm {Proj}} F[X, Y, Z, W]$
is defined by the equation
$X \hookrightarrow \mathbb P^3_{F}= \operatorname {\mathrm {Proj}} F[X, Y, Z, W]$
is defined by the equation
where
 $$ \begin{align*} f_0(X, Y, W)&:= p_2 X - 2Y + q_2 W, \\ f_1(X, Y, W)&:= p_1 XW + q_1 W^2, \\ f_2(X, Y, W)&:= X^3 +p_0 XW^2 + q_0 W^3 - Y^2W. \end{align*} $$
$$ \begin{align*} f_0(X, Y, W)&:= p_2 X - 2Y + q_2 W, \\ f_1(X, Y, W)&:= p_1 XW + q_1 W^2, \\ f_2(X, Y, W)&:= X^3 +p_0 XW^2 + q_0 W^3 - Y^2W. \end{align*} $$
Proof. See [Reference ShiodaShi95, Theorem 14]. Although the result is stated in characteristic
![]() $0$
in [Reference ShiodaShi95], the same result holds in characteristic
$0$
in [Reference ShiodaShi95], the same result holds in characteristic
![]() $p \geq 11$
, as claimed before [Reference ShiodaShi95, Lemma 13].
$p \geq 11$
, as claimed before [Reference ShiodaShi95, Lemma 13].
One can check that none of the
![]() $27$
elements
$27$
elements
![]() $a_i, a^{\prime }_i, a^{\prime \prime }_{ij}$
are zero. It follows from [Reference ShiodaShi95, Theorem 15] that the point
$a_i, a^{\prime }_i, a^{\prime \prime }_{ij}$
are zero. It follows from [Reference ShiodaShi95, Theorem 15] that the point
![]() $P:=[0, 0, 1, 0] \in X$
is not contained in any line in
$P:=[0, 0, 1, 0] \in X$
is not contained in any line in
![]() $X_{\overline {F}}$
. Then, as explained in Example 4.4, the morphism
$X_{\overline {F}}$
. Then, as explained in Example 4.4, the morphism
induced by the projection onto
![]() $\mathbb P^2_{F} = (Z=0) \subset \mathbb P^3_{F}$
expresses
$\mathbb P^2_{F} = (Z=0) \subset \mathbb P^3_{F}$
expresses
![]() $\mathrm {Bl}_P (X)$
as a double covering of
$\mathrm {Bl}_P (X)$
as a double covering of
![]() $\mathbb P^2_{F}$
whose ramification locus
$\mathbb P^2_{F}$
whose ramification locus
![]() $C \subset \mathbb P^2_{F}$
is a smooth quartic curve.
$C \subset \mathbb P^2_{F}$
is a smooth quartic curve.
Lemma 4.8. The curve C is defined by the equation
Proof. This is a well-known fact, but let us sketch the proof for the convenience of the reader. We first note that the morphism
![]() $\mathrm {Bl}_P (X) \to \mathbb P^2_{F}$
maps the exceptional divisor isomorphically onto the line in
$\mathrm {Bl}_P (X) \to \mathbb P^2_{F}$
maps the exceptional divisor isomorphically onto the line in
![]() $\mathbb P^2_{F}$
defined by
$\mathbb P^2_{F}$
defined by
![]() $f_0=0$
. The locus in
$f_0=0$
. The locus in
![]() $\mathbb P^2_{F}$
where the geometric fibers of the projection
$\mathbb P^2_{F}$
where the geometric fibers of the projection
![]() $X - \{ P \} \to \mathbb P^2_{F}$
are empty is the locus where
$X - \{ P \} \to \mathbb P^2_{F}$
are empty is the locus where
![]() $f_0=f_1=0$
. (The locus where
$f_0=f_1=0$
. (The locus where
![]() $f_0=f_1=f_2=0$
is empty by the condition that
$f_0=f_1=f_2=0$
is empty by the condition that
![]() $P \in X$
is not contained in any line in
$P \in X$
is not contained in any line in
![]() $X_{\overline {F}}$
.) The locus in
$X_{\overline {F}}$
.) The locus in
![]() $\mathbb P^2_{F}$
where the geometric fibers of
$\mathbb P^2_{F}$
where the geometric fibers of
![]() $X - \{ P \} \to \mathbb P^2_{F}$
have exactly one point is the union of
$X - \{ P \} \to \mathbb P^2_{F}$
have exactly one point is the union of
and
It follows that the ramification locus
![]() $C \subset \mathbb P^2_{F}$
(or equivalently, the locus where the geometric fibers of
$C \subset \mathbb P^2_{F}$
(or equivalently, the locus where the geometric fibers of
![]() $\mathrm {Bl}_P (X) \to \mathbb P^2_{F}$
have exactly one point) is defined by
$\mathrm {Bl}_P (X) \to \mathbb P^2_{F}$
have exactly one point) is defined by
![]() $g=0$
.
$g=0$
.
The polynomial
![]() $g(X, Y, W)$
lives in
$g(X, Y, W)$
lives in
![]() $\mathcal {O}_F[X, Y, W]$
. We shall prove the following claim.
$\mathcal {O}_F[X, Y, W]$
. We shall prove the following claim.
Lemma 4.9. The closed subscheme
![]() $\mathscr {C} \subset \mathbb P^2_{\mathcal {O}_F}$
defined by
$\mathscr {C} \subset \mathbb P^2_{\mathcal {O}_F}$
defined by
![]() $g(X, Y, W)=0$
is a stable curve over
$g(X, Y, W)=0$
is a stable curve over
![]() $\mathcal {O}_F$
.
$\mathcal {O}_F$
.
Proof. We first note that g is an irreducible element of
![]() $\mathcal {O}_F[X, Y, W]$
since it is irreducible in
$\mathcal {O}_F[X, Y, W]$
since it is irreducible in
![]() $F[X, Y, W]$
and is not divisible by the uniformizer t. It follows that
$F[X, Y, W]$
and is not divisible by the uniformizer t. It follows that
![]() $\mathscr {C}$
is irreducible, which in turn implies that it is flat over
$\mathscr {C}$
is irreducible, which in turn implies that it is flat over
![]() $\mathcal {O}_F$
.
$\mathcal {O}_F$
.
Let
![]() $\overline {a} \in \mathbb F_q$
denote the image of an element
$\overline {a} \in \mathbb F_q$
denote the image of an element
![]() $a \in \mathcal {O}_F$
. (We also use this notation for polynomials.) One can check that the polynomial
$a \in \mathcal {O}_F$
. (We also use this notation for polynomials.) One can check that the polynomial
![]() $\sum ^{27}_{m=0} \overline {\varepsilon }_{27-m} S^{m} \in \mathbb F_q[S]$
is equal to
$\sum ^{27}_{m=0} \overline {\varepsilon }_{27-m} S^{m} \in \mathbb F_q[S]$
is equal to
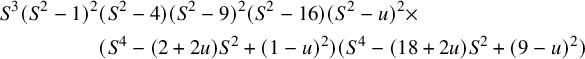 $$ \begin{align} \begin{aligned} S^3(S^2-1)^2&(S^2-4)(S^2-9)^2(S^2-16)(S^2-u)^2 \times \\ &(S^4-(2+2u)S^2+(1-u)^2)(S^4-(18+2u)S^2+(9-u)^2) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} S^3(S^2-1)^2&(S^2-4)(S^2-9)^2(S^2-16)(S^2-u)^2 \times \\ &(S^4-(2+2u)S^2+(1-u)^2)(S^4-(18+2u)S^2+(9-u)^2) \end{aligned} \end{align} $$
if
![]() $(q-1)/2$
is even, and is equal to
$(q-1)/2$
is even, and is equal to
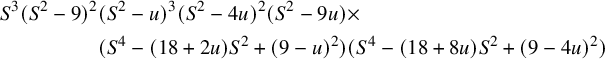 $$ \begin{align} \begin{aligned} S^3(S^2-9)^2&(S^2-u)^3(S^2-4u)^2(S^2-9u) \times \\ &(S^4-(18+2u)S^2+(9-u)^2)(S^4-(18+8u)S^2+(9-4u)^2) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} S^3(S^2-9)^2&(S^2-u)^3(S^2-4u)^2(S^2-9u) \times \\ &(S^4-(18+2u)S^2+(9-u)^2)(S^4-(18+8u)S^2+(9-4u)^2) \end{aligned} \end{align} $$
if
![]() $(q-1)/2$
is odd. It follows that
$(q-1)/2$
is odd. It follows that
![]() $\overline {p}_1=\overline {q}_1=0$
, and the special fiber of
$\overline {p}_1=\overline {q}_1=0$
, and the special fiber of
![]() $\mathscr {C}$
is defined by
$\mathscr {C}$
is defined by
The special fiber has two irreducible components
![]() $\overline {\mathscr {C}}_1$
and
$\overline {\mathscr {C}}_1$
and
![]() $\overline {\mathscr {C}}_2$
: the first one
$\overline {\mathscr {C}}_2$
: the first one
![]() $\overline {\mathscr {C}}_1$
is the line defined by
$\overline {\mathscr {C}}_1$
is the line defined by
![]() $\overline {f_0}=0$
, and the second one
$\overline {f_0}=0$
, and the second one
![]() $\overline {\mathscr {C}}_2$
is a cubic curve of Weierstrass form, defined by
$\overline {\mathscr {C}}_2$
is a cubic curve of Weierstrass form, defined by
![]() $\overline {f_2}=0$
. We can check that the discriminant of
$\overline {f_2}=0$
. We can check that the discriminant of
![]() $\overline {\mathscr {C}}_2$
is zero and that the
$\overline {\mathscr {C}}_2$
is zero and that the
![]() $c_4$
invariant of
$c_4$
invariant of
![]() $\overline {\mathscr {C}}_2$
is
$\overline {\mathscr {C}}_2$
is
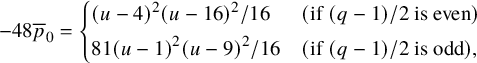 $$ \begin{align} -48\overline{p}_0= \left\{ \begin{aligned} & (u-4)^2(u-16)^2/16 & (& \text{if } (q-1)/2 \text{ is even})\\ & 81(u-1)^2(u-9)^2/16 & (& \text{if } (q-1)/2 \text{ is odd}), \end{aligned} \right. \end{align} $$
$$ \begin{align} -48\overline{p}_0= \left\{ \begin{aligned} & (u-4)^2(u-16)^2/16 & (& \text{if } (q-1)/2 \text{ is even})\\ & 81(u-1)^2(u-9)^2/16 & (& \text{if } (q-1)/2 \text{ is odd}), \end{aligned} \right. \end{align} $$
which is nonzero since
![]() $\sqrt {u}$
is not contained in
$\sqrt {u}$
is not contained in
![]() $\mathbb F_q$
. Therefore,
$\mathbb F_q$
. Therefore,
![]() $\overline {\mathscr {C}}_2$
is a nodal curve; see [Reference SilvermanSil09, Chapter III, Proposition 1.4]. (The
$\overline {\mathscr {C}}_2$
is a nodal curve; see [Reference SilvermanSil09, Chapter III, Proposition 1.4]. (The
![]() $c_4$
invariant of a cubic curve of Weierstrass form is defined at the beginning of [Reference SilvermanSil09, Section III.1].) In order to show that
$c_4$
invariant of a cubic curve of Weierstrass form is defined at the beginning of [Reference SilvermanSil09, Section III.1].) In order to show that
![]() $\mathscr {C}$
is a stable curve, it suffices to show that
$\mathscr {C}$
is a stable curve, it suffices to show that
![]() $(\overline {\mathscr {C}}_1)_{\overline {\mathbb F}_p}$
intersects with
$(\overline {\mathscr {C}}_1)_{\overline {\mathbb F}_p}$
intersects with
![]() $(\overline {\mathscr {C}}_2)_{\overline {\mathbb F}_p}$
in exactly three points. Since they do not intersect each other in
$(\overline {\mathscr {C}}_2)_{\overline {\mathbb F}_p}$
in exactly three points. Since they do not intersect each other in
![]() $W=0$
, it is enough to show that the discriminant of the polynomial
$W=0$
, it is enough to show that the discriminant of the polynomial
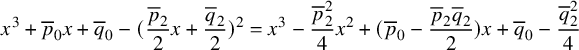 $$ \begin{align} x^3 + \overline{p}_0 x + \overline{q}_0 -(\frac{\overline{p}_2}{2} x + \frac{\overline{q}_2}{2})^2=x^3 -\frac{\overline{p}^2_2}{4} x^2 + (\overline{p}_0 - \frac{\overline{p}_2\overline{q}_2}{2})x + \overline{q}_0 -\frac{\overline{q}^2_2}{4} \end{align} $$
$$ \begin{align} x^3 + \overline{p}_0 x + \overline{q}_0 -(\frac{\overline{p}_2}{2} x + \frac{\overline{q}_2}{2})^2=x^3 -\frac{\overline{p}^2_2}{4} x^2 + (\overline{p}_0 - \frac{\overline{p}_2\overline{q}_2}{2})x + \overline{q}_0 -\frac{\overline{q}^2_2}{4} \end{align} $$
is nonzero. The discriminant is equal to
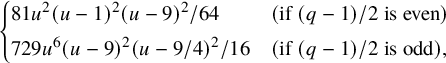 $$ \begin{align} \left\{ \begin{aligned} & 81u^2(u-1)^2(u-9)^2/64 & (& \text{if } (q-1)/2 \text{ is even})\\ & 729u^6(u-9)^2(u-9/4)^2/16 & (& \text{if } (q-1)/2 \text{ is odd}), \end{aligned} \right. \end{align} $$
$$ \begin{align} \left\{ \begin{aligned} & 81u^2(u-1)^2(u-9)^2/64 & (& \text{if } (q-1)/2 \text{ is even})\\ & 729u^6(u-9)^2(u-9/4)^2/16 & (& \text{if } (q-1)/2 \text{ is odd}), \end{aligned} \right. \end{align} $$
which is nonzero since
![]() $\sqrt {u}$
is not contained in
$\sqrt {u}$
is not contained in
![]() $\mathbb F_q$
.
$\mathbb F_q$
.
Remark 4.10.
-
1. One can compute the discriminant of
 $\overline {\mathscr {C}}_2$
, the
$\overline {\mathscr {C}}_2$
, the
 $c_4$
invariant of
$c_4$
invariant of
 $\overline {\mathscr {C}}_2$
, and the discriminant of (4) by using a computer algebra software. More precisely, we consider the polynomial
$\overline {\mathscr {C}}_2$
, and the discriminant of (4) by using a computer algebra software. More precisely, we consider the polynomial
 $Q(u, S)$
with coefficients in
$Q(u, S)$
with coefficients in
 $R:=\mathbb Z[1/(2 \cdot 3 \cdot 5 \cdot 7)]$
defined as in (1) or (2) (depending on whether
$R:=\mathbb Z[1/(2 \cdot 3 \cdot 5 \cdot 7)]$
defined as in (1) or (2) (depending on whether
 $(q-1)/2$
is even or odd). Here, we regard u as a variable. Let
$(q-1)/2$
is even or odd). Here, we regard u as a variable. Let
 $\varepsilon _m \in R[u]$
be the coefficient of
$\varepsilon _m \in R[u]$
be the coefficient of
 $S^{27-m}$
in
$S^{27-m}$
in
 $Q(u, S)$
, and we define
$Q(u, S)$
, and we define
 $p_2, p_1, q_2, p_0, q_1, q_0 \in R[u]$
in the same way as above. Then one can check that in the ring
$p_2, p_1, q_2, p_0, q_1, q_0 \in R[u]$
in the same way as above. Then one can check that in the ring
 $R[u]$
, the discriminant of the elliptic curve over
$R[u]$
, the discriminant of the elliptic curve over
 $R[u]$
defined by
$R[u]$
defined by
 $X^3 +p_0 XW^2 + q_0 W^3 - Y^2W$
is zero, and its
$X^3 +p_0 XW^2 + q_0 W^3 - Y^2W$
is zero, and its
 $c_4$
invariant has the form of (3). Moreover, one can show that the discriminant of the cubic polynomial with coefficients in
$c_4$
invariant has the form of (3). Moreover, one can show that the discriminant of the cubic polynomial with coefficients in
 $R[u]$
defined in the same way as (4) has the form of (5).
$R[u]$
defined in the same way as (4) has the form of (5). -
2. We can more easily prove the following weaker statement, which is in fact enough for our purpose (i.e., the proof of Theorem 4.14): For a large enough q, there exists an element
 $u \in \mathbb F_q^\times $
such that
$u \in \mathbb F_q^\times $
such that
 $\sqrt {u}$
is not contained in
$\sqrt {u}$
is not contained in
 $\mathbb F_q$
and the closed subscheme
$\mathbb F_q$
and the closed subscheme
 $\mathscr {C} \subset \mathbb P^2_{\mathcal {O}_F}$
as in Lemma 4.9 is a stable curve over
$\mathscr {C} \subset \mathbb P^2_{\mathcal {O}_F}$
as in Lemma 4.9 is a stable curve over
 $\mathcal {O}_F$
. To see this, we remark that, in fact, the vanishing of the discriminant of
$\mathcal {O}_F$
. To see this, we remark that, in fact, the vanishing of the discriminant of
 $\overline {\mathscr {C}}_2$
is not necessary once we know that the
$\overline {\mathscr {C}}_2$
is not necessary once we know that the
 $c_4$
invariant is nonzero (since this implies that
$c_4$
invariant is nonzero (since this implies that
 $\overline {\mathscr {C}}_2$
is a smooth curve or a nodal curve). One can check that the
$\overline {\mathscr {C}}_2$
is a smooth curve or a nodal curve). One can check that the
 $c_4$
invariant and the discriminant of (4) have nonzero polynomial expressions in u with coefficients in
$c_4$
invariant and the discriminant of (4) have nonzero polynomial expressions in u with coefficients in
 $\mathbb F_q$
. Since the degrees of these polynomials are bounded uniformly for q, it follows that for a large enough q, there exists an element
$\mathbb F_q$
. Since the degrees of these polynomials are bounded uniformly for q, it follows that for a large enough q, there exists an element
 $u \in \mathbb F_q^\times $
such that
$u \in \mathbb F_q^\times $
such that
 $\sqrt {u}$
is not contained in
$\sqrt {u}$
is not contained in
 $\mathbb F_q$
and u is not a root of any of these polynomials. This proves our claim.
$\mathbb F_q$
and u is not a root of any of these polynomials. This proves our claim.
In total, we have shown the following statement:
Lemma 4.11. There exists a smooth quartic curve
![]() $C \subset \mathbb P^2_{F}$
over
$C \subset \mathbb P^2_{F}$
over
![]() $F=\mathbb F_q((t))$
with the following properties:
$F=\mathbb F_q((t))$
with the following properties:
-
•
 $\gamma (C) \in \operatorname {\mathrm {Br}}(F)[2]$
is nonzero.
$\gamma (C) \in \operatorname {\mathrm {Br}}(F)[2]$
is nonzero. -
• C has stable reduction over
 $\mathcal {O}_F=\mathbb F_q[[t]]$
.
$\mathcal {O}_F=\mathbb F_q[[t]]$
.
Remark 4.12. We found smooth quartic curves as in Lemma 4.11 through trial and error. It would be interesting to give a more conceptual way to construct such smooth quartic curves.
Corollary 4.13. Let p be a prime such that
![]() $p \geq 11$
.
$p \geq 11$
.
-
1.
 $\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{3, \mathbb F_q})[2]=0$
for any finite field
$\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{3, \mathbb F_q})[2]=0$
for any finite field
 $\mathbb F_q$
of characteristic p.
$\mathbb F_q$
of characteristic p. -
2.
 $\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{3, \overline {\mathbb F}_p})[2]=0$
.
$\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{3, \overline {\mathbb F}_p})[2]=0$
.
Proof. (1) By [Reference Lorenzo and PirisiLP24], we have
![]() $\operatorname {\mathrm {Br}}(\mathcal {M}_{3, \mathbb F_q})[2] \simeq \mathbb Z/2\mathbb Z$
. Let
$\operatorname {\mathrm {Br}}(\mathcal {M}_{3, \mathbb F_q})[2] \simeq \mathbb Z/2\mathbb Z$
. Let
![]() $\gamma \in \operatorname {\mathrm {Br}}(\mathcal {M}_{3, \mathbb F_q})[2]$
be the nonzero element. It suffices to show that
$\gamma \in \operatorname {\mathrm {Br}}(\mathcal {M}_{3, \mathbb F_q})[2]$
be the nonzero element. It suffices to show that
![]() $\gamma $
does not lie in the image of
$\gamma $
does not lie in the image of
![]() $\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{3, \mathbb F_q}) \hookrightarrow \operatorname {\mathrm {Br}}(\mathcal {M}_{3, \mathbb F_q})$
. This follows from Lemma 4.11 since
$\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{3, \mathbb F_q}) \hookrightarrow \operatorname {\mathrm {Br}}(\mathcal {M}_{3, \mathbb F_q})$
. This follows from Lemma 4.11 since
![]() $\operatorname {\mathrm {Br}}(\mathbb {F}_{q}[[t]])=0$
.
$\operatorname {\mathrm {Br}}(\mathbb {F}_{q}[[t]])=0$
.
(2) This follows from (1).
We can now prove the desired statement:
Theorem 4.14. We have
![]() $\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{3, \overline {\mathbb Q}})=0$
.
$\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{3, \overline {\mathbb Q}})=0$
.
Proof. By [Reference Lorenzo and PirisiLP24], we have
![]() $\operatorname {\mathrm {Br}}(\mathcal {M}_{3, \overline {\mathbb Q}}) \simeq \mathbb Z/2\mathbb Z$
. Since
$\operatorname {\mathrm {Br}}(\mathcal {M}_{3, \overline {\mathbb Q}}) \simeq \mathbb Z/2\mathbb Z$
. Since
![]() $\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{3, \overline {\mathbb Q}})$
is embedded into
$\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{3, \overline {\mathbb Q}})$
is embedded into
![]() $\operatorname {\mathrm {Br}}(\mathcal {M}_{3, \overline {\mathbb Q}})$
, by virtue of Remark 3.9 and Lemma 3.10, it suffices to show that
$\operatorname {\mathrm {Br}}(\mathcal {M}_{3, \overline {\mathbb Q}})$
, by virtue of Remark 3.9 and Lemma 3.10, it suffices to show that
![]() $\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{3, \overline {\mathbb F}_p})[2]=0$
for some odd prime p. This follows from Corollary 4.13.
$\operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{3, \overline {\mathbb F}_p})[2]=0$
for some odd prime p. This follows from Corollary 4.13.
4.4 Genus greater than or equal to four
We conclude this paper by recalling the following well-known vanishing for the case
![]() $g \geq 4$
, together with a rough explanation of where the condition that
$g \geq 4$
, together with a rough explanation of where the condition that
![]() $g \geq 4$
is used.
$g \geq 4$
is used.
Theorem 4.15 (Korkmaz-Stipsicz).
Assume that
![]() $g\geq 4$
and n arbitrary. Then
$g\geq 4$
and n arbitrary. Then
![]() $ \operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{g,n,\overline {\mathbb {Q}}})=0. $
$ \operatorname {\mathrm {Br}}(\overline {\mathcal {M}}_{g,n,\overline {\mathbb {Q}}})=0. $
Proof. As in the proof of Proposition 4.1, it is enough to show that
![]() $\operatorname {\mathrm {Br}}(\mathcal {M}_{g,n,\mathbb {C}})=0.$
This vanishing is explained in [Reference Fringuelli and PirisiFP21, Theorem 4.1] and is due to Korkmaz-Stipsicz and Harer: The key point is that
$\operatorname {\mathrm {Br}}(\mathcal {M}_{g,n,\mathbb {C}})=0.$
This vanishing is explained in [Reference Fringuelli and PirisiFP21, Theorem 4.1] and is due to Korkmaz-Stipsicz and Harer: The key point is that
which reduces to a computation in group homology and this is [Reference Korkmaz and StipsiczKS03, Theorem 1.1] (where they rely crucially on a stablization result due to Harer [Reference HarerHar85], where the restriction
![]() $g\geq 4$
enters).
$g\geq 4$
enters).
Acknowledgements
The authors would like to thank Kęstutis Česnavičius and Jochen Heinloth for very helpful discussions. The first author (S.B.) wants to thank Stefan Schröer for giving an interesting talk on his work [Reference SchröerSch23] in Essen, which inspired some arguments in Section 3. Finally, the authors would like to thank the referee for carefully reading the manuscript and for providing helpful comments.
Competing interest
The authors have no competing interests to declare.
Financial support
The authors both acknowledge financial supports by DFG RTG 2553 and JSPS KAKENHI Grant Number 24H00015. The work of the second author (K.I.) was also supported by JSPS KAKENHI Grant Number 24K16887.