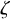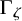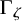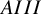1. Introduction and description of results
1.1. Background and motivation
Let
![]() $\mathfrak {g}$
be a finite-dimensional quasi-reductive Lie superalgebra over
$\mathfrak {g}$
be a finite-dimensional quasi-reductive Lie superalgebra over
![]() ${\mathbb {C}}$
with a triangular decomposition
${\mathbb {C}}$
with a triangular decomposition
in the sense of [Reference MazorchukMa] (see also [Reference Chen, Cheng and CoulembierCCC]). Here,
![]() $\mathfrak {h}$
is a purely even Cartan subalgebra with nil- and opposite radical
$\mathfrak {h}$
is a purely even Cartan subalgebra with nil- and opposite radical
![]() $\mathfrak n^\pm $
, respectively. Let
$\mathfrak n^\pm $
, respectively. Let
![]() $Z(\mathfrak {g}_{\bar 0})$
be the center of the universal enveloping algebra
$Z(\mathfrak {g}_{\bar 0})$
be the center of the universal enveloping algebra
![]() $U(\mathfrak {g}_{\bar 0})$
of
$U(\mathfrak {g}_{\bar 0})$
of
![]() $\mathfrak {g}_{\bar 0}$
. Motivated by earlier results of Kostant [Reference KostantKo], Miličić-Soergel [Reference Miličić and SoergelMSo] and Backelin [Reference BackelinBac], Mazorchuk and the authors [Reference ChenCh1, Reference ChenCh2, Reference Chen, Cheng and MazorchukCCM2] studied the category
$\mathfrak {g}_{\bar 0}$
. Motivated by earlier results of Kostant [Reference KostantKo], Miličić-Soergel [Reference Miličić and SoergelMSo] and Backelin [Reference BackelinBac], Mazorchuk and the authors [Reference ChenCh1, Reference ChenCh2, Reference Chen, Cheng and MazorchukCCM2] studied the category
![]() $\mathcal N$
consisting of finitely generated
$\mathcal N$
consisting of finitely generated
![]() $\mathfrak {g}$
-modules that are locally finite over
$\mathfrak {g}$
-modules that are locally finite over
![]() $Z(\mathfrak {g}_{\bar 0})$
and
$Z(\mathfrak {g}_{\bar 0})$
and
![]() $U(\mathfrak n^+)$
, which we refer to as Whittaker modules over
$U(\mathfrak n^+)$
, which we refer to as Whittaker modules over
![]() $\mathfrak {g}$
. The category
$\mathfrak {g}$
. The category
![]() $\mathcal N$
decomposes into a direct sum of the full subcategories
$\mathcal N$
decomposes into a direct sum of the full subcategories
![]() $\mathcal N(\zeta )$
, with
$\mathcal N(\zeta )$
, with
![]() $\zeta \in \mathrm {ch}\mathfrak n^+_{\bar 0}:{=}\left (\mathfrak n_{\bar 0}^+/[\mathfrak n_{\bar 0}^+,\mathfrak n_{\bar 0}^+]\right )^*$
, consisting of modules
$\zeta \in \mathrm {ch}\mathfrak n^+_{\bar 0}:{=}\left (\mathfrak n_{\bar 0}^+/[\mathfrak n_{\bar 0}^+,\mathfrak n_{\bar 0}^+]\right )^*$
, consisting of modules
![]() $M\in \mathcal N$
on which
$M\in \mathcal N$
on which
![]() $x-\zeta (x)$
acts locally nilpotently, for any
$x-\zeta (x)$
acts locally nilpotently, for any
![]() $x\in \mathfrak n^+_{\bar 0}$
. Furthermore, the category
$x\in \mathfrak n^+_{\bar 0}$
. Furthermore, the category
![]() $\mathcal N(\zeta )$
is a union of certain full subcategories
$\mathcal N(\zeta )$
is a union of certain full subcategories
![]() $\mathcal N(\zeta )^n$
, for
$\mathcal N(\zeta )^n$
, for
![]() $n\geq 1$
, in the sense of [Reference ChenCh1, Section 4.1.2], which extends the definition in [Reference Miličić and SoergelMSo, Section 5] for Lie algebras. In particular,
$n\geq 1$
, in the sense of [Reference ChenCh1, Section 4.1.2], which extends the definition in [Reference Miličić and SoergelMSo, Section 5] for Lie algebras. In particular,
![]() $\mathcal N(\zeta )^1$
contains all simple objects in
$\mathcal N(\zeta )^1$
contains all simple objects in
![]() $\mathcal N(\zeta )$
, and
$\mathcal N(\zeta )$
, and
![]() $\mathcal N(0)^1$
coincides with the Bernstein-Gelfand-Gelfand (BGG) category
$\mathcal N(0)^1$
coincides with the Bernstein-Gelfand-Gelfand (BGG) category
![]() ${\mathcal {O}}$
. Therefore, the category
${\mathcal {O}}$
. Therefore, the category
![]() $\mathcal N(\zeta )^1$
provides a suitable framework for the study of Whittaker modules. In the present paper, we introduce an integral block
$\mathcal N(\zeta )^1$
provides a suitable framework for the study of Whittaker modules. In the present paper, we introduce an integral block
![]() $\mathcal W(\zeta )$
of
$\mathcal W(\zeta )$
of
![]() $\mathcal N(\zeta )^1$
(see Section 2.6). In particular,
$\mathcal N(\zeta )^1$
(see Section 2.6). In particular,
![]() $\mathcal W(0)$
coincides with the integral BGG category
$\mathcal W(0)$
coincides with the integral BGG category
![]() ${\mathcal {O}}_{\mathbb Z}$
.
${\mathcal {O}}_{\mathbb Z}$
.
For Lie superalgebras, the standard Whittaker modules
![]() $M(\lambda ,\zeta )\in \mathcal N(\zeta )$
were introduced in [Reference Bagci, Christodoulopoulou and WiesnerBCW, Reference ChenCh1],
$M(\lambda ,\zeta )\in \mathcal N(\zeta )$
were introduced in [Reference Bagci, Christodoulopoulou and WiesnerBCW, Reference ChenCh1],
![]() $\lambda \in \mathfrak {h}^\ast $
. These modules were initially studied by McDowell [Reference McDowellMc1, Reference McDowellMc2] and Miličić-Soergel [Reference Miličić and SoergelMSo] for Lie algebras. They are generalizations of Verma modules and play an analogous role in the representation theory of
$\lambda \in \mathfrak {h}^\ast $
. These modules were initially studied by McDowell [Reference McDowellMc1, Reference McDowellMc2] and Miličić-Soergel [Reference Miličić and SoergelMSo] for Lie algebras. They are generalizations of Verma modules and play an analogous role in the representation theory of
![]() $\mathcal W(\zeta )$
.
$\mathcal W(\zeta )$
.
A quasi-reductive Lie superalgebra
![]() $\mathfrak {g}$
is said to be of type I if
$\mathfrak {g}$
is said to be of type I if
![]() $\mathfrak {g}$
has a
$\mathfrak {g}$
has a
![]() ${\mathbb Z}_2$
-compatible
${\mathbb Z}_2$
-compatible
![]() ${\mathbb Z}$
-gradation of the form
${\mathbb Z}$
-gradation of the form
![]() $\mathfrak {g}=\mathfrak {g}_{-1}\oplus \mathfrak {g}_0\oplus \mathfrak {g}_1$
. In this case, the standard Whittaker modules and the Whittaker category
$\mathfrak {g}=\mathfrak {g}_{-1}\oplus \mathfrak {g}_0\oplus \mathfrak {g}_1$
. In this case, the standard Whittaker modules and the Whittaker category
![]() $\mathcal W(\zeta )$
have been investigated by the first author [Reference ChenCh1], and then by Mazorchuk and the authors [Reference Chen, Cheng and MazorchukCCM2]. In particular, for the general linear Lie superalgebra
$\mathcal W(\zeta )$
have been investigated by the first author [Reference ChenCh1], and then by Mazorchuk and the authors [Reference Chen, Cheng and MazorchukCCM2]. In particular, for the general linear Lie superalgebra
![]() $\mathfrak {gl}(m|n)$
, the composition multiplicity of standard Whittaker modules is controlled by the Brundan-Kazhdan-Lusztig polynomials from [Reference BrundanBr2, Reference Cheng, Lam and WangCLW]. Furthermore, it was shown in [Reference Chen, Cheng and MazorchukCCM2] that
$\mathfrak {gl}(m|n)$
, the composition multiplicity of standard Whittaker modules is controlled by the Brundan-Kazhdan-Lusztig polynomials from [Reference BrundanBr2, Reference Cheng, Lam and WangCLW]. Furthermore, it was shown in [Reference Chen, Cheng and MazorchukCCM2] that
![]() $\mathcal W(\zeta )$
categorifies a q-symmetrized Fock space over a quantum group of type A in the case
$\mathcal W(\zeta )$
categorifies a q-symmetrized Fock space over a quantum group of type A in the case
![]() $\mathfrak {g}=\mathfrak {gl}(m|n)$
.
$\mathfrak {g}=\mathfrak {gl}(m|n)$
.
A main motivation for the present paper is to study the multiplicities of composition factors of standard Whittaker modules and a corresponding categorification picture using the Whittaker categories
![]() $\mathcal W(\zeta )$
for Lie superalgebras beyond type I.
$\mathcal W(\zeta )$
for Lie superalgebras beyond type I.
1.2. Setup
Throughout this paper, we let
![]() $\mathfrak {g}$
be an arbitrary finite-dimensional quasi-reductive Lie superalgebra. This means that
$\mathfrak {g}$
be an arbitrary finite-dimensional quasi-reductive Lie superalgebra. This means that
![]() $\mathfrak {g}_{\bar 0}$
is a reductive Lie algebra and
$\mathfrak {g}_{\bar 0}$
is a reductive Lie algebra and
![]() $\mathfrak {g}_{\bar 1}$
is semisimple as a
$\mathfrak {g}_{\bar 1}$
is semisimple as a
![]() $\mathfrak {g}_{\bar 0}$
-module. We fix a triangular decomposition of
$\mathfrak {g}_{\bar 0}$
-module. We fix a triangular decomposition of
![]() $\mathfrak {g}$
as given in (1.1). The corresponding Borel subalgebra is defined to be
$\mathfrak {g}$
as given in (1.1). The corresponding Borel subalgebra is defined to be
![]() $\mathfrak b:=\mathfrak h\oplus \mathfrak n^+$
. We are mainly interested in the following examples of quasi-reductive Lie superalgebras in Kac’s list [Reference KacKac]:
$\mathfrak b:=\mathfrak h\oplus \mathfrak n^+$
. We are mainly interested in the following examples of quasi-reductive Lie superalgebras in Kac’s list [Reference KacKac]:
We refer to, for example, [Reference Cheng and WangCW, Reference MussonMu2] for more details on the structure of these Lie superalgebras.
For each root
![]() $\alpha $
of
$\alpha $
of
![]() $\mathfrak {g}$
, we denote by
$\mathfrak {g}$
, we denote by
![]() $\mathfrak {g}_\alpha :=\{x\in \mathfrak {g}|~ hx=\alpha (h)x, \text { for all }h\in \mathfrak {h}\}$
, the corresponding root space. For
$\mathfrak {g}_\alpha :=\{x\in \mathfrak {g}|~ hx=\alpha (h)x, \text { for all }h\in \mathfrak {h}\}$
, the corresponding root space. For
![]() $\zeta \in \mathrm {ch}\mathfrak n_{\bar 0}^+$
, we denote by
$\zeta \in \mathrm {ch}\mathfrak n_{\bar 0}^+$
, we denote by
![]() $\Pi _\zeta $
the set of all roots
$\Pi _\zeta $
the set of all roots
![]() $\alpha $
in
$\alpha $
in
![]() $\mathfrak n^+_{\bar 0}$
with
$\mathfrak n^+_{\bar 0}$
with
![]() $\zeta (\mathfrak {g}_\alpha )\neq 0.$
This leads to a Levi subalgebra
$\zeta (\mathfrak {g}_\alpha )\neq 0.$
This leads to a Levi subalgebra
![]() $\mathfrak l_\zeta $
of
$\mathfrak l_\zeta $
of
![]() $\mathfrak {g}_{\bar 0}$
; that is,
$\mathfrak {g}_{\bar 0}$
; that is,
![]() $\mathfrak l_\zeta $
is generated by
$\mathfrak l_\zeta $
is generated by
![]() $\mathfrak h$
and
$\mathfrak h$
and
![]() $\mathfrak {g}_{\pm \alpha }$
for
$\mathfrak {g}_{\pm \alpha }$
for
![]() $\alpha \in \Pi _\zeta $
.
$\alpha \in \Pi _\zeta $
.
In this paper, unless otherwise specified, we shall assume that
![]() $\mathfrak l_\zeta $
is a Levi subalgebra in a parabolic decomposition in the sense of [Reference MazorchukMa, Section 2.4] (in particular,
$\mathfrak l_\zeta $
is a Levi subalgebra in a parabolic decomposition in the sense of [Reference MazorchukMa, Section 2.4] (in particular,
![]() $\zeta $
can be extended trivially to a character of
$\zeta $
can be extended trivially to a character of
![]() $\mathfrak n^+$
):
$\mathfrak n^+$
):
which is compatible with the triangular decomposition given in (1.1) – namely,
![]() $\mathfrak u^\pm \subseteq \mathfrak n^\pm $
. That is, there exists
$\mathfrak u^\pm \subseteq \mathfrak n^\pm $
. That is, there exists
![]() $H\in \mathfrak {h}$
such that
$H\in \mathfrak {h}$
such that
such that
![]() $\mathrm {Re}\alpha (H)\geq 0,~\text {for any root } \alpha $
in
$\mathrm {Re}\alpha (H)\geq 0,~\text {for any root } \alpha $
in
![]() $\mathfrak n^+,$
where
$\mathfrak n^+,$
where
![]() $\mathrm {Re}(z)$
denotes the real part of
$\mathrm {Re}(z)$
denotes the real part of
![]() $z\in {\mathbb {C}}$
; see also [Reference ChenCh1, Section 3.3] for examples. We let
$z\in {\mathbb {C}}$
; see also [Reference ChenCh1, Section 3.3] for examples. We let
![]() $\mathfrak {p}:=\mathfrak {l}_\zeta +\mathfrak {u}^+$
be the corresponding parabolic subalgebra. We remark that if one starts with a character
$\mathfrak {p}:=\mathfrak {l}_\zeta +\mathfrak {u}^+$
be the corresponding parabolic subalgebra. We remark that if one starts with a character
![]() $\zeta \in \mathrm {ch} {\mathfrak n^+_{\bar 0}}$
which leads to a parabolic decomposition in (1.4), then there exists a compatible triangular decomposition of
$\zeta \in \mathrm {ch} {\mathfrak n^+_{\bar 0}}$
which leads to a parabolic decomposition in (1.4), then there exists a compatible triangular decomposition of
![]() $\mathfrak {g}$
; see [Reference Chen, Cheng and CoulembierCCC, Lemma 1.3]. We note that H lies in the center of
$\mathfrak {g}$
; see [Reference Chen, Cheng and CoulembierCCC, Lemma 1.3]. We note that H lies in the center of
![]() $\mathfrak l_\zeta $
. In this article, we exclude the family of queer Lie superalgebras.
$\mathfrak l_\zeta $
. In this article, we exclude the family of queer Lie superalgebras.
Motivated by the equivalences of categories in the earlier works of Bernstein-Gelfand [Reference Bernstein and GelfandBG] and Miličić-Soergel [Reference Miličić and SoergelMSo], which connect modules in
![]() ${\mathcal {O}}$
and Whittaker modules in
${\mathcal {O}}$
and Whittaker modules in
![]() $\mathcal N$
, an equivalence is established in [Reference ChenCh1, Reference ChenCh2] between
$\mathcal N$
, an equivalence is established in [Reference ChenCh1, Reference ChenCh2] between
![]() $\mathcal W(\zeta )$
and a certain full subcategory
$\mathcal W(\zeta )$
and a certain full subcategory
![]() $\mathcal {\mathcal {O}}^{\zeta \text {-pres}}$
of
$\mathcal {\mathcal {O}}^{\zeta \text {-pres}}$
of
![]() ${\mathcal {O}}_{\mathbb Z}$
(see Section 2.4). The objects in
${\mathcal {O}}_{\mathbb Z}$
(see Section 2.4). The objects in
![]() $\mathcal {\mathcal {O}}^{\zeta \text {-pres}}$
admit a two step resolution by projective modules whose simple quotients are free
$\mathcal {\mathcal {O}}^{\zeta \text {-pres}}$
admit a two step resolution by projective modules whose simple quotients are free
![]() $U(\mathfrak {g}_{-\alpha })$
-modules, for any
$U(\mathfrak {g}_{-\alpha })$
-modules, for any
![]() $\alpha \in \Pi _\zeta $
.
$\alpha \in \Pi _\zeta $
.
1.3. Goal
An important task in the study of Whittaker modules is to find the composition factors of a given standard Whittaker module. In the case of reductive Lie algebras, Miličić and Soergel developed in [Reference Miličić and SoergelMSo] an equivalence between
![]() $\mathcal N(\zeta )$
and certain category of Harish-Chandra bimodules to provide an answer for the composition multiplicity of
$\mathcal N(\zeta )$
and certain category of Harish-Chandra bimodules to provide an answer for the composition multiplicity of
![]() $M(\lambda ,\zeta )$
for regular and integral weights
$M(\lambda ,\zeta )$
for regular and integral weights
![]() $\lambda $
. Subsequently, Backelin in [Reference BackelinBac] introduced an exact functor
$\lambda $
. Subsequently, Backelin in [Reference BackelinBac] introduced an exact functor
![]() $\Gamma _\zeta $
from
$\Gamma _\zeta $
from
![]() ${\mathcal {O}}$
to
${\mathcal {O}}$
to
![]() $\mathcal N(\zeta )$
, sending Verma modules to standard Whittaker modules, to give a complete solution in terms of Kazhdan-Lusztig polynomials.
$\mathcal N(\zeta )$
, sending Verma modules to standard Whittaker modules, to give a complete solution in terms of Kazhdan-Lusztig polynomials.
Standard Whittaker modules for Lie superalgebras of type I, which are of finite length, were originally considered in [Reference Bagci, Christodoulopoulou and WiesnerBCW]. However, as a complete classification of simple Whittaker modules was not available at that time, limited effort had been made to resolve the problem of finding composition multiplicity for standard Whittaker modules over Lie superalgebras until recently. It is proved in [Reference ChenCh1] that in type I case, this multiplicity problem reduces to that of Verma modules in
![]() ${\mathcal {O}}$
; see also [Reference Brundan and GoodwinBrG] for a special nonsingular case. In particular, in the case of
${\mathcal {O}}$
; see also [Reference Brundan and GoodwinBrG] for a special nonsingular case. In particular, in the case of
![]() $\mathfrak {g}=\mathfrak {gl}(m|n)$
, these multiplicities can be computed by means of Brundan-Kazhdan-Lusztig polynomials [Reference Brundan and MasonBr3, Reference Cheng, Lam and WangCLW]; see also [Reference Chen, Cheng and MazorchukCCM2].
$\mathfrak {g}=\mathfrak {gl}(m|n)$
, these multiplicities can be computed by means of Brundan-Kazhdan-Lusztig polynomials [Reference Brundan and MasonBr3, Reference Cheng, Lam and WangCLW]; see also [Reference Chen, Cheng and MazorchukCCM2].
When the Lie superalgebra is not of type I, standard Whittaker modules similarly as in McDowell [Reference McDowellMc1, Reference McDowellMc2] can also be defined under the assumption that
![]() $\zeta $
satisfies the assumption in Section 1.2. This is done in [Reference ChenCh1] and also in the present paper.
$\zeta $
satisfies the assumption in Section 1.2. This is done in [Reference ChenCh1] and also in the present paper.
By [Reference ChenCh1, Theorem 6], for any
![]() $\lambda \in \mathfrak h^\ast $
, the top of the standard Whittaker
$\lambda \in \mathfrak h^\ast $
, the top of the standard Whittaker
![]() $M(\lambda , \zeta )$
is simple, which we denote by
$M(\lambda , \zeta )$
is simple, which we denote by
![]() $L(\lambda ,\zeta )$
. These simple Whittaker modules are classified in terms of orbits in
$L(\lambda ,\zeta )$
. These simple Whittaker modules are classified in terms of orbits in
![]() $\mathfrak {h}^\ast $
under the dot-action of the Weyl group
$\mathfrak {h}^\ast $
under the dot-action of the Weyl group
![]() $W_\zeta $
of
$W_\zeta $
of
![]() $\mathfrak l_\zeta $
, and they constitute all simple objects in
$\mathfrak l_\zeta $
, and they constitute all simple objects in
![]() $\mathcal N(\zeta )$
. One of the main objectives of this paper is to provide a complete answer to the composition multiplicity problem for standard Whittaker modules over quasi-reductive Lie superalgebras beyond type I.
$\mathcal N(\zeta )$
. One of the main objectives of this paper is to provide a complete answer to the composition multiplicity problem for standard Whittaker modules over quasi-reductive Lie superalgebras beyond type I.
1.4. Main results
For each
![]() $M\in {\mathcal {O}}$
, we denote the completion of M with respect to its weight spaces by
$M\in {\mathcal {O}}$
, we denote the completion of M with respect to its weight spaces by
![]() $\overline M:=\prod _{\lambda \in \mathfrak h^\ast } M_\lambda $
. Then, the module
$\overline M:=\prod _{\lambda \in \mathfrak h^\ast } M_\lambda $
. Then, the module
![]() $\Gamma _\zeta (M)$
is defined to be the submodule of
$\Gamma _\zeta (M)$
is defined to be the submodule of
![]() $\overline {M}$
consisting of vectors annihilated by a power of
$\overline {M}$
consisting of vectors annihilated by a power of
![]() $x-\zeta (x)$
, for all
$x-\zeta (x)$
, for all
![]() $x\in \mathfrak n^+_{\bar 0}$
. Then
$x\in \mathfrak n^+_{\bar 0}$
. Then
![]() $\Gamma _\zeta $
defines an exact functor from
$\Gamma _\zeta $
defines an exact functor from
![]() ${\mathcal {O}}$
to
${\mathcal {O}}$
to
![]() $\mathcal N(\zeta )$
, which we refer to as the Backelin functor associated to
$\mathcal N(\zeta )$
, which we refer to as the Backelin functor associated to
![]() $\zeta $
for
$\zeta $
for
![]() $\mathfrak {g}$
. Let
$\mathfrak {g}$
. Let
![]() $M(\lambda )$
be the Verma module of highest weight
$M(\lambda )$
be the Verma module of highest weight
![]() $\lambda $
with respect to the triangular decomposition (1.1) and
$\lambda $
with respect to the triangular decomposition (1.1) and
![]() $L(\lambda )$
its unique simple quotient. Our first main result is the following.
$L(\lambda )$
its unique simple quotient. Our first main result is the following.
Theorem 1 (Proposition 4, Theorem 6-(ii)).
For any weight
![]() $\lambda \in \mathfrak {h}^\ast $
, the Backelin functor
$\lambda \in \mathfrak {h}^\ast $
, the Backelin functor
![]() $\Gamma _\zeta (-)$
sends
$\Gamma _\zeta (-)$
sends
![]() $M(\lambda )$
to
$M(\lambda )$
to
![]() $M(\lambda ,\zeta )$
. Furthermore,
$M(\lambda ,\zeta )$
. Furthermore,
![]() $\Gamma _\zeta (-)$
sends
$\Gamma _\zeta (-)$
sends
![]() $L(\lambda )$
to
$L(\lambda )$
to
![]() $L(\lambda ,\zeta )$
, if
$L(\lambda ,\zeta )$
, if
![]() $\lambda $
is
$\lambda $
is
![]() $W_\zeta $
-anti-dominant, and to zero otherwise.
$W_\zeta $
-anti-dominant, and to zero otherwise.
Consequently, we have the following multiplicity formula:
for
![]() $W_\zeta $
-anti-dominant weights
$W_\zeta $
-anti-dominant weights
![]() $\lambda , \mu $
.
$\lambda , \mu $
.
Any Lie superalgebra from the series
![]() $\mathfrak {gl}(m|n),~{\mathfrak {sl}}(m|n),~{\mathfrak {osp}}(2|2n)$
and
$\mathfrak {gl}(m|n),~{\mathfrak {sl}}(m|n),~{\mathfrak {osp}}(2|2n)$
and
![]() $\mathfrak p(n)$
in (1.2) admits a
$\mathfrak p(n)$
in (1.2) admits a
![]() ${\mathbb Z}_2$
-compatible gradation
${\mathbb Z}_2$
-compatible gradation
![]() $\mathfrak {g}= \mathfrak {g}_{-1}\oplus \mathfrak {g}_0 \oplus \mathfrak {g}_1$
(i.e., they are Lie superalgebras of type I). In this case, Theorem 1 recovers (and provides a uniform proof of) [Reference ChenCh1, Thoerem C].
$\mathfrak {g}= \mathfrak {g}_{-1}\oplus \mathfrak {g}_0 \oplus \mathfrak {g}_1$
(i.e., they are Lie superalgebras of type I). In this case, Theorem 1 recovers (and provides a uniform proof of) [Reference ChenCh1, Thoerem C].
Recently, an
![]() $\imath $
-canonical basis theory based on a quantum symmetric pair
$\imath $
-canonical basis theory based on a quantum symmetric pair
![]() $(U,U^\imath )$
has been systematically developed by Bao and Wang starting with the pioneering work [Reference Bao and WangBW], which extends Lusztig’s canonical basis theory for quantum groups [Reference LusztigLu1, Reference LusztigLu2]. The main motivation of [Reference Bao and WangBW] was to resolve the irreducible character problem in the integral BGG category
$(U,U^\imath )$
has been systematically developed by Bao and Wang starting with the pioneering work [Reference Bao and WangBW], which extends Lusztig’s canonical basis theory for quantum groups [Reference LusztigLu1, Reference LusztigLu2]. The main motivation of [Reference Bao and WangBW] was to resolve the irreducible character problem in the integral BGG category
![]() ${\mathcal {O}}_{\mathbb Z}$
for the ortho-symplectic Lie superalgebra. For
${\mathcal {O}}_{\mathbb Z}$
for the ortho-symplectic Lie superalgebra. For
![]() $\mathfrak {osp}(2m+1|2n)$
, the
$\mathfrak {osp}(2m+1|2n)$
, the
![]() $\imath $
-canonical basis theory of the associated
$\imath $
-canonical basis theory of the associated
![]() $\imath $
-quantum group
$\imath $
-quantum group
![]() $U^\imath $
(see Section 5.1) on a completed Fock space
$U^\imath $
(see Section 5.1) on a completed Fock space
![]() $\widehat {\mathbb {T}}^{m|n}$
(see Section 5.2) provides a complete solution to this problem in subcategory
$\widehat {\mathbb {T}}^{m|n}$
(see Section 5.2) provides a complete solution to this problem in subcategory
![]() ${\mathcal {O}}^{\texttt {int}}_{\mathbb Z}$
of integer weight modules (see Section 6). In this case, the corresponding quantum symmetric pair
${\mathcal {O}}^{\texttt {int}}_{\mathbb Z}$
of integer weight modules (see Section 6). In this case, the corresponding quantum symmetric pair
![]() $(U,U^\imath )$
is quasi-split of type
$(U,U^\imath )$
is quasi-split of type
![]() $AIII$
. In particular, the linear isomorphism
$AIII$
. In particular, the linear isomorphism
![]() $\psi $
from
$\psi $
from
![]() $\widehat {\mathbb {T}}^{m|n}$
to a corresponding completed Grothendieck group
$\widehat {\mathbb {T}}^{m|n}$
to a corresponding completed Grothendieck group
![]() $\widehat {K}({\mathcal {O}}^{\texttt {int}}_{\mathbb {Z}})_{\mathbb {Q}}$
, sending standard monomial basis elements to Verma modules, match the
$\widehat {K}({\mathcal {O}}^{\texttt {int}}_{\mathbb {Z}})_{\mathbb {Q}}$
, sending standard monomial basis elements to Verma modules, match the
![]() $\imath $
-canonical and dual
$\imath $
-canonical and dual
![]() $\imath $
-canonical bases with tilting and simple objects, respectively. A similar solution to the irreducible character problem in the subcategory
$\imath $
-canonical bases with tilting and simple objects, respectively. A similar solution to the irreducible character problem in the subcategory
![]() ${\mathcal {O}}^{\texttt {hf}}_{\mathbb Z}$
of half-integer weight modules (see again Section 6) is given in terms of so-called
${\mathcal {O}}^{\texttt {hf}}_{\mathbb Z}$
of half-integer weight modules (see again Section 6) is given in terms of so-called
![]() $\jmath $
-canonical basis [Reference Bao and WangBW, Chapter 12]. Note that this together solves the irreducible character problem in
$\jmath $
-canonical basis [Reference Bao and WangBW, Chapter 12]. Note that this together solves the irreducible character problem in
![]() ${\mathcal {O}}_{\mathbb Z}$
, as other integral weights are typical.
${\mathcal {O}}_{\mathbb Z}$
, as other integral weights are typical.
In the present paper, we study a certain q-symmetrized Fock space
![]() $\widehat {\mathbb {T}}^{m|n}_{\zeta }$
, depending on the character
$\widehat {\mathbb {T}}^{m|n}_{\zeta }$
, depending on the character
![]() $\zeta \in \mathrm {ch} \mathfrak n_{\bar 0}^+$
, which can be regarded either as a
$\zeta \in \mathrm {ch} \mathfrak n_{\bar 0}^+$
, which can be regarded either as a
![]() $U^\imath $
-submodule or as a
$U^\imath $
-submodule or as a
![]() $U^\imath $
-quotient of
$U^\imath $
-quotient of
![]() $\widehat {\mathbb {T}}^{m|n}$
. There is a canonical q-symmetrizer map
$\widehat {\mathbb {T}}^{m|n}$
. There is a canonical q-symmetrizer map
![]() $\phi _\zeta :\widehat {\mathbb {T}}^{m|n}\rightarrow \widehat {\mathbb {T}}^{m|n}_\zeta $
. Building on the works of [Reference Bao and WangBW], we construct in a natural way
$\phi _\zeta :\widehat {\mathbb {T}}^{m|n}\rightarrow \widehat {\mathbb {T}}^{m|n}_\zeta $
. Building on the works of [Reference Bao and WangBW], we construct in a natural way
![]() $\imath $
-canonical and dual
$\imath $
-canonical and dual
![]() $\imath $
-canonical bases on this q-symmetrized Fock space. We show that the
$\imath $
-canonical bases on this q-symmetrized Fock space. We show that the
![]() $U^\imath $
-module
$U^\imath $
-module
![]() $\widehat {\mathbb {T}}^{m|n}_\zeta $
is categorified by an ‘integer weight’ subcategory
$\widehat {\mathbb {T}}^{m|n}_\zeta $
is categorified by an ‘integer weight’ subcategory
![]() $\mathcal W(\zeta )^{\texttt {int}}$
(see Section 7.2) of our category
$\mathcal W(\zeta )^{\texttt {int}}$
(see Section 7.2) of our category
![]() $\mathcal W(\zeta )$
, when
$\mathcal W(\zeta )$
, when
![]() $\mathfrak g$
is the ortho-symplectic Lie superalgebra
$\mathfrak g$
is the ortho-symplectic Lie superalgebra
![]() $\mathfrak {osp}(2m+1|2n)$
. The linear action of
$\mathfrak {osp}(2m+1|2n)$
. The linear action of
![]() $U^\imath $
on the Fock space at
$U^\imath $
on the Fock space at
![]() $q=1$
translates to action of certain translation functors on the category. We denote by
$q=1$
translates to action of certain translation functors on the category. We denote by
![]() $\psi _\zeta $
the induced isomorphism from
$\psi _\zeta $
the induced isomorphism from
![]() $\widehat {\mathbb {T}}^{m|n}_{\zeta ,q=1}$
to the completed Grothendieck group
$\widehat {\mathbb {T}}^{m|n}_{\zeta ,q=1}$
to the completed Grothendieck group
![]() $\widehat {K}(\mathcal W(\zeta )^{\texttt {int}})_{\mathbb {Q}}$
. We can now state our second main result, which is equivalent to Theorem 31 below.
$\widehat {K}(\mathcal W(\zeta )^{\texttt {int}})_{\mathbb {Q}}$
. We can now state our second main result, which is equivalent to Theorem 31 below.
Theorem 2. Let
![]() $\mathfrak {g}$
be
$\mathfrak {g}$
be
![]() $\mathfrak {osp}(2m+1|2n)$
. Let
$\mathfrak {osp}(2m+1|2n)$
. Let
![]() $\gamma _\zeta :\widehat {K}({\mathcal {O}}^{\texttt {int}}_{\mathbb {Z}})_{\mathbb {Q}}\rightarrow \widehat {K}(\mathcal W(\zeta )^{\texttt {int}})_{\mathbb {Q}}$
be the map induced by the Backelin functor
$\gamma _\zeta :\widehat {K}({\mathcal {O}}^{\texttt {int}}_{\mathbb {Z}})_{\mathbb {Q}}\rightarrow \widehat {K}(\mathcal W(\zeta )^{\texttt {int}})_{\mathbb {Q}}$
be the map induced by the Backelin functor
![]() $\Gamma _\zeta $
. We have the following commutative diagram of
$\Gamma _\zeta $
. We have the following commutative diagram of
![]() $U^\imath _{q=1}$
-homomorphisms:
$U^\imath _{q=1}$
-homomorphisms:

Furthermore, the map
![]() $\psi _\zeta $
matches
$\psi _\zeta $
matches
![]() $\imath $
-canonical and dual
$\imath $
-canonical and dual
![]() $\imath $
-canonical basis with the tilting and simple objects in
$\imath $
-canonical basis with the tilting and simple objects in
![]() $\mathcal W(\zeta )^{\texttt {int}}$
, respectively.
$\mathcal W(\zeta )^{\texttt {int}}$
, respectively.
There is also an analogue of Theorem 2 in the case of half-integer weight subcategory
![]() $\mathcal W(\zeta )^{\texttt {hf}}$
of
$\mathcal W(\zeta )^{\texttt {hf}}$
of
![]() $\mathcal W(\zeta )$
formulated in Theorem 32. In this case, it is formulated in terms of so-called
$\mathcal W(\zeta )$
formulated in Theorem 32. In this case, it is formulated in terms of so-called
![]() $\jmath $
-canonical basis. Also, we have counterparts for the Lie superalgebra
$\jmath $
-canonical basis. Also, we have counterparts for the Lie superalgebra
![]() $\mathfrak {osp}(2m|2n)$
. Therefore, Theorem 2, its half-integer and their type D counterparts together give an ortho-symplectic analogue of the results in [Reference Chen, Cheng and MazorchukCCM2, Section 3.7] for type A Lie superalgebras.
$\mathfrak {osp}(2m|2n)$
. Therefore, Theorem 2, its half-integer and their type D counterparts together give an ortho-symplectic analogue of the results in [Reference Chen, Cheng and MazorchukCCM2, Section 3.7] for type A Lie superalgebras.
1.5. Additional results
1.5.1. Homomorphisms from
 $M(\lambda ,\zeta )$
to full dual of Verma modules
$M(\lambda ,\zeta )$
to full dual of Verma modules
Suppose that
![]() $\mathfrak {g}$
is a Lie superalgebra in Kac’s list (1.2) with
$\mathfrak {g}$
is a Lie superalgebra in Kac’s list (1.2) with
![]() $\mathfrak {g}\neq \mathfrak {p} (n)$
. For any
$\mathfrak {g}\neq \mathfrak {p} (n)$
. For any
![]() $\lambda \in \mathfrak {h}^\ast $
, we define
$\lambda \in \mathfrak {h}^\ast $
, we define
![]() $N(\lambda )$
to be the Verma module of lowest weight
$N(\lambda )$
to be the Verma module of lowest weight
![]() $\lambda $
with respect to
$\lambda $
with respect to
![]() $\mathfrak b$
– namely,
$\mathfrak b$
– namely,
![]() $N(\lambda ):=\operatorname {Ind}\nolimits _{\mathfrak {h}+\mathfrak n^-}^{\mathfrak {g}}{\mathbb {C}}_\lambda $
. We note that
$N(\lambda ):=\operatorname {Ind}\nolimits _{\mathfrak {h}+\mathfrak n^-}^{\mathfrak {g}}{\mathbb {C}}_\lambda $
. We note that
![]() $N(-\lambda )^\ast \cong \mathrm { Coind}^{\mathfrak {g}}_{\mathfrak h+\mathfrak n^-}{\mathbb {C}}_\lambda $
; see, for example, [Reference ScheunertSch, Chapter 4]. Also, we let
$N(-\lambda )^\ast \cong \mathrm { Coind}^{\mathfrak {g}}_{\mathfrak h+\mathfrak n^-}{\mathbb {C}}_\lambda $
; see, for example, [Reference ScheunertSch, Chapter 4]. Also, we let
![]() $M(\lambda )^{\ast ,\tau }$
be the full dual of the Verma module
$M(\lambda )^{\ast ,\tau }$
be the full dual of the Verma module
![]() $M(\lambda )$
with the action of
$M(\lambda )$
with the action of
![]() $\mathfrak {g}$
twisted by the Chevalley antiautomorphism
$\mathfrak {g}$
twisted by the Chevalley antiautomorphism
![]() $\tau $
on
$\tau $
on
![]() $\mathfrak {g}$
.
$\mathfrak {g}$
.
In Theorem 6(i), we prove that, for
![]() $\lambda ,\mu \in \mathfrak {h}^\ast $
and
$\lambda ,\mu \in \mathfrak {h}^\ast $
and
![]() $M = N(-\mu )^\ast $
or
$M = N(-\mu )^\ast $
or
![]() $M(\mu )^{\ast ,\tau }$
, we have
$M(\mu )^{\ast ,\tau }$
, we have
 $$ \begin{align} &\operatorname{Hom}\nolimits_{\mathfrak{g}}(M(\lambda,\zeta), M)= \left\{\begin{array}{ll} {\mathbb{C}}, & \text{~for } \mu\in W_\zeta\cdot \lambda;\\ 0, & \text{ otherwise}. \end{array} \right. \end{align} $$
$$ \begin{align} &\operatorname{Hom}\nolimits_{\mathfrak{g}}(M(\lambda,\zeta), M)= \left\{\begin{array}{ll} {\mathbb{C}}, & \text{~for } \mu\in W_\zeta\cdot \lambda;\\ 0, & \text{ otherwise}. \end{array} \right. \end{align} $$
Here,
![]() $W_\zeta \cdot \lambda $
denotes the orbit of
$W_\zeta \cdot \lambda $
denotes the orbit of
![]() $\lambda $
under the dot-action
$\lambda $
under the dot-action
![]() $\cdot $
of the Weyl group
$\cdot $
of the Weyl group
![]() $W_\zeta $
of
$W_\zeta $
of
![]() $\mathfrak l_\zeta $
on
$\mathfrak l_\zeta $
on
![]() $\mathfrak h^\ast $
. In particular, this extends [Reference Brown and RomanovBR, Theorem 5.2], where the case of semisimple Lie algebras with regular weight
$\mathfrak h^\ast $
. In particular, this extends [Reference Brown and RomanovBR, Theorem 5.2], where the case of semisimple Lie algebras with regular weight
![]() $\lambda $
was considered.
$\lambda $
was considered.
1.5.2. A realization of the Serre quotient functor
The categories
![]() $\mathcal W(\zeta )$
and
$\mathcal W(\zeta )$
and
![]() ${\mathcal {O}}^{\zeta \text {-pres}}$
fit naturally into the framework of the Serre quotient category
${\mathcal {O}}^{\zeta \text {-pres}}$
fit naturally into the framework of the Serre quotient category
![]() ${\overline {{\mathcal {O}}}}$
in the sense of Gabriel [Reference GabrielGa], which is a localization of
${\overline {{\mathcal {O}}}}$
in the sense of Gabriel [Reference GabrielGa], which is a localization of
![]() ${\mathcal {O}}_{\mathbb Z}$
with the canonical quotient functor
${\mathcal {O}}_{\mathbb Z}$
with the canonical quotient functor
![]() $\pi : {\mathcal {O}}_{\mathbb Z}\rightarrow {\overline {{\mathcal {O}}}}$
with respect to the set of homomorphisms with kernels and cokernels lying in a given Serre subcategory. In the case of Lie superalgebras of type I, it is proved in [Reference Chen, Cheng and MazorchukCCM2] that the Backelin functor
$\pi : {\mathcal {O}}_{\mathbb Z}\rightarrow {\overline {{\mathcal {O}}}}$
with respect to the set of homomorphisms with kernels and cokernels lying in a given Serre subcategory. In the case of Lie superalgebras of type I, it is proved in [Reference Chen, Cheng and MazorchukCCM2] that the Backelin functor
![]() $\Gamma _\zeta (-)$
is a realization of the quotient functor
$\Gamma _\zeta (-)$
is a realization of the quotient functor
![]() $\pi $
. In this paper, we extend this result to any Lie superalgebras
$\pi $
. In this paper, we extend this result to any Lie superalgebras
![]() $\mathfrak {g}$
in Kac’s list (1.2).
$\mathfrak {g}$
in Kac’s list (1.2).
1.5.3. Annihilator ideals of simple Whittaker modules
It is proved that every primitive ideal of a quasi-reductive Lie superalgebra is the annihilator of some simple highest weight modules; see, for example, [Reference DufloDu, Reference LetzterLe1, Reference MussonMu1, Reference Chen and CoulembierCC]. In the case of
![]() $W_\zeta =W$
, Kostant [Reference KostantKo, Theorem 3.9] gives a description of the annihilator ideals for simple Whittaker modules over semisimple Lie algebras. This has been extended to Lie superalgebras of type I in [Reference ChenCh2, Theorem B]. In this paper, we will prove an analogue for any Lie superalgebra
$W_\zeta =W$
, Kostant [Reference KostantKo, Theorem 3.9] gives a description of the annihilator ideals for simple Whittaker modules over semisimple Lie algebras. This has been extended to Lie superalgebras of type I in [Reference ChenCh2, Theorem B]. In this paper, we will prove an analogue for any Lie superalgebra
![]() $\mathfrak {g}$
in Kac’s list (1.2).
$\mathfrak {g}$
in Kac’s list (1.2).
1.6. Organization
The paper is organized as follows. In Section 2, we provide the necessary preliminaries. In particular, we introduce various (equivalent) abelian categories, including the Whittaker categories
![]() $\mathcal W(\zeta )$
. In Section 3, we give a proof of Theorem 1. Section 4 is devoted to a description of the stratified structure on
$\mathcal W(\zeta )$
. In Section 3, we give a proof of Theorem 1. Section 4 is devoted to a description of the stratified structure on
![]() $\mathcal W(\zeta )$
. In particular, we describe explicitly the tilting modules in
$\mathcal W(\zeta )$
. In particular, we describe explicitly the tilting modules in
![]() $\mathcal W(\zeta )$
and prove a BGG type reciprocity for
$\mathcal W(\zeta )$
and prove a BGG type reciprocity for
![]() $\mathcal W(\zeta )$
. In Section 5, we study a q-symmetrized Fock space over the
$\mathcal W(\zeta )$
. In Section 5, we study a q-symmetrized Fock space over the
![]() $\imath $
-quantum group mentioned earlier and construct its
$\imath $
-quantum group mentioned earlier and construct its
![]() $\imath $
-canonical and the dual
$\imath $
-canonical and the dual
![]() $\imath $
-canonical bases on this space. We briefly recall in Section 6 the solution of the irreducible character problem for the ortho-symplectic Lie superalgebras in category
$\imath $
-canonical bases on this space. We briefly recall in Section 6 the solution of the irreducible character problem for the ortho-symplectic Lie superalgebras in category
![]() ${\mathcal {O}}$
, which we then use in Section 7 to complete the proof of Theorem 2.
${\mathcal {O}}$
, which we then use in Section 7 to complete the proof of Theorem 2.
2. Preliminaries
In this section, we review the necessary background and definitions that will be used in the remainder of the paper.
2.1. Root systems and Weyl group
Let
![]() $\Phi $
be the set of all roots. Denote by
$\Phi $
be the set of all roots. Denote by
![]() $\Pi $
,
$\Pi $
,
![]() $\Phi ^\pm $
,
$\Phi ^\pm $
,
![]() $\Phi _{{\bar 0}}$
and
$\Phi _{{\bar 0}}$
and
![]() $\Phi _{\bar 1}$
the sets of simple, positive/negative, even and odd roots of
$\Phi _{\bar 1}$
the sets of simple, positive/negative, even and odd roots of
![]() $\mathfrak {g}$
, respectively. Define
$\mathfrak {g}$
, respectively. Define
![]() $\Phi _\epsilon ^\pm :=\Phi _\epsilon \cap \Phi ^\pm $
,
$\Phi _\epsilon ^\pm :=\Phi _\epsilon \cap \Phi ^\pm $
,
![]() $\epsilon =\bar {0},\bar {1}$
. Set
$\epsilon =\bar {0},\bar {1}$
. Set
![]() $\Pi _{\bar 0}$
to be the simple system for
$\Pi _{\bar 0}$
to be the simple system for
![]() $\Phi _{\bar 0}^+$
. For each
$\Phi _{\bar 0}^+$
. For each
![]() $\alpha \in \Phi $
, we denote by
$\alpha \in \Phi $
, we denote by
![]() $\mathfrak {g}_\alpha $
the root space of
$\mathfrak {g}_\alpha $
the root space of
![]() $\mathfrak {g}$
corresponding to
$\mathfrak {g}$
corresponding to
![]() $\alpha $
. The corresponding Borel subalgebra is
$\alpha $
. The corresponding Borel subalgebra is
![]() $\mathfrak b=\mathfrak h\oplus \mathfrak n^+$
, with
$\mathfrak b=\mathfrak h\oplus \mathfrak n^+$
, with
![]() $\mathfrak n^+=\bigoplus _{\alpha \in \Phi ^+}\mathfrak {g}_\alpha $
.
$\mathfrak n^+=\bigoplus _{\alpha \in \Phi ^+}\mathfrak {g}_\alpha $
.
Recall that we fixed a character
![]() $\zeta $
that gives rise to a Levi subalgebra
$\zeta $
that gives rise to a Levi subalgebra
![]() $\mathfrak l_\zeta $
of
$\mathfrak l_\zeta $
of
![]() $\mathfrak {g}$
as given in Section 1.2. Also, recall that the set of all simple roots of
$\mathfrak {g}$
as given in Section 1.2. Also, recall that the set of all simple roots of
![]() $\mathfrak l_\zeta $
is denoted as follows
$\mathfrak l_\zeta $
is denoted as follows
We note that
![]() $\zeta ([\mathfrak n^+_{\bar 1}, \mathfrak n^+_{\bar 1}])=0$
, the latter implies that
$\zeta ([\mathfrak n^+_{\bar 1}, \mathfrak n^+_{\bar 1}])=0$
, the latter implies that
![]() $\zeta $
extends trivially to a one-dimensional
$\zeta $
extends trivially to a one-dimensional
![]() $\mathfrak n^+$
-module. We also denote by
$\mathfrak n^+$
-module. We also denote by
![]() $\zeta $
the induced algebra homomorphism from
$\zeta $
the induced algebra homomorphism from
![]() $U(\mathfrak n^+)$
to
$U(\mathfrak n^+)$
to
![]() ${\mathbb {C}}$
.
${\mathbb {C}}$
.
The Weyl group W is defined to be the Weyl group of
![]() $\mathfrak g_{\bar 0}$
, and it acts naturally on
$\mathfrak g_{\bar 0}$
, and it acts naturally on
![]() $\mathfrak {h}^\ast $
. For each
$\mathfrak {h}^\ast $
. For each
![]() $\alpha \in \Pi _{\bar 0}$
, let
$\alpha \in \Pi _{\bar 0}$
, let
![]() $s_\alpha \in W$
be the simple reflection corresponding to
$s_\alpha \in W$
be the simple reflection corresponding to
![]() $\alpha $
. We consider the dot-action of W on
$\alpha $
. We consider the dot-action of W on
![]() $\mathfrak {h}^\ast $
; that is,
$\mathfrak {h}^\ast $
; that is,
![]() $w\cdot \lambda := w(\lambda +\rho _{\bar 0})-\rho _{\bar 0}$
, for any
$w\cdot \lambda := w(\lambda +\rho _{\bar 0})-\rho _{\bar 0}$
, for any
![]() $w\in W$
and
$w\in W$
and
![]() $\lambda \in \mathfrak {h}^\ast $
. Here,
$\lambda \in \mathfrak {h}^\ast $
. Here,
![]() $\rho _{\bar 0}$
denotes the half-sum of all positive even roots. Also, we let
$\rho _{\bar 0}$
denotes the half-sum of all positive even roots. Also, we let
![]() $W_\zeta $
denote the Weyl group of
$W_\zeta $
denote the Weyl group of
![]() $\mathfrak l_\zeta $
. We denote by
$\mathfrak l_\zeta $
. We denote by
![]() $w_0$
and
$w_0$
and
![]() $w_0^\zeta $
the longest elements in W and
$w_0^\zeta $
the longest elements in W and
![]() $W_\zeta $
, respectively.
$W_\zeta $
, respectively.
Fix a W-invariant nondegenerate bilinear form
![]() $(\cdot ,\cdot )$
on
$(\cdot ,\cdot )$
on
![]() $\mathfrak {h}^\ast $
. For each
$\mathfrak {h}^\ast $
. For each
![]() $\alpha \in \Phi _{\bar 0}^+$
, we set
$\alpha \in \Phi _{\bar 0}^+$
, we set
![]() $\alpha ^\vee :=2\alpha /(\alpha ,\alpha )$
. A weight
$\alpha ^\vee :=2\alpha /(\alpha ,\alpha )$
. A weight
![]() $\lambda $
is called integral if
$\lambda $
is called integral if
![]() $(\lambda ,\alpha ^\vee )\in {\mathbb Z}$
for all roots
$(\lambda ,\alpha ^\vee )\in {\mathbb Z}$
for all roots
![]() $\alpha \in \Phi _{\bar 0}$
. Let
$\alpha \in \Phi _{\bar 0}$
. Let
![]() $\Lambda $
be the set of integral weights. For any given
$\Lambda $
be the set of integral weights. For any given
![]() $\alpha \in \Phi _{\bar 0}^+$
, a weight
$\alpha \in \Phi _{\bar 0}^+$
, a weight
![]() $\lambda $
is called
$\lambda $
is called
![]() $\alpha $
-dominant (respectively,
$\alpha $
-dominant (respectively,
![]() $\alpha $
-anti-dominant) if
$\alpha $
-anti-dominant) if
![]() $(\lambda +\rho _{\bar 0},\alpha ^\vee )\notin {\mathbb Z}_{<0}$
(respectively,
$(\lambda +\rho _{\bar 0},\alpha ^\vee )\notin {\mathbb Z}_{<0}$
(respectively,
![]() $(\lambda +\rho _{\bar 0},\alpha ^\vee )\notin {\mathbb Z}_{>0}$
). We denote by
$(\lambda +\rho _{\bar 0},\alpha ^\vee )\notin {\mathbb Z}_{>0}$
). We denote by
![]() ${\Lambda (\zeta )}$
the set of all integral weights that are
${\Lambda (\zeta )}$
the set of all integral weights that are
![]() $\alpha $
-anti-dominant, for all
$\alpha $
-anti-dominant, for all
![]() $\alpha \in \Pi _\zeta $
.
$\alpha \in \Pi _\zeta $
.
2.2. Induction and restriction functors
We denote by
![]() $U(\mathfrak {g})$
the universal enveloping algebra of
$U(\mathfrak {g})$
the universal enveloping algebra of
![]() $\mathfrak {g}$
and
$\mathfrak {g}$
and
![]() $Z(\mathfrak {g})$
its center. For any
$Z(\mathfrak {g})$
its center. For any
![]() $\lambda \in \mathfrak {h}^\ast $
, we denote by
$\lambda \in \mathfrak {h}^\ast $
, we denote by
![]() $\chi _\lambda : Z(\mathfrak {g})\rightarrow {\mathbb {C}}$
the central character associated with
$\chi _\lambda : Z(\mathfrak {g})\rightarrow {\mathbb {C}}$
the central character associated with
![]() $\lambda $
. Denote by
$\lambda $
. Denote by
![]() $\mathfrak {g}\operatorname {-mod}\nolimits $
the category of all
$\mathfrak {g}\operatorname {-mod}\nolimits $
the category of all
![]() $\mathfrak {g}$
-modules. For any subalgebra
$\mathfrak {g}$
-modules. For any subalgebra
![]() $\mathfrak s\subseteq \mathfrak {g}$
, we have the exact restriction, induction and coinduction functors
$\mathfrak s\subseteq \mathfrak {g}$
, we have the exact restriction, induction and coinduction functors
In the case
![]() $\mathfrak {g}_{\bar 0}=\mathfrak s$
, we use the notations
$\mathfrak {g}_{\bar 0}=\mathfrak s$
, we use the notations
![]() $\operatorname {Res}\nolimits (-):= \operatorname {Res}\nolimits _{\mathfrak {g}_{\bar 0}}^{\mathfrak {g}}(-)$
,
$\operatorname {Res}\nolimits (-):= \operatorname {Res}\nolimits _{\mathfrak {g}_{\bar 0}}^{\mathfrak {g}}(-)$
,
![]() $\operatorname {Ind}\nolimits (-):= \operatorname {Ind}\nolimits _{\mathfrak {g}_{\bar 0}}^{\mathfrak {g}}(-)$
and
$\operatorname {Ind}\nolimits (-):= \operatorname {Ind}\nolimits _{\mathfrak {g}_{\bar 0}}^{\mathfrak {g}}(-)$
and
![]() $\mathrm {Coind}(-):= \mathrm {Coind}_{\mathfrak {g}_{\bar 0}}^{\mathfrak {g}}(-)$
. By [Reference Bell and FarnsteinerBF, Theorem 2.2] (see also [Reference GorelikGo1]),
$\mathrm {Coind}(-):= \mathrm {Coind}_{\mathfrak {g}_{\bar 0}}^{\mathfrak {g}}(-)$
. By [Reference Bell and FarnsteinerBF, Theorem 2.2] (see also [Reference GorelikGo1]),
![]() $\operatorname {Ind}\nolimits (-)$
is isomorphic to
$\operatorname {Ind}\nolimits (-)$
is isomorphic to
![]() $\mathrm {Coind}(-)$
up to tensoring with the one-dimensional
$\mathrm {Coind}(-)$
up to tensoring with the one-dimensional
![]() $\mathfrak {g}_{\bar 0}$
-module
$\mathfrak {g}_{\bar 0}$
-module
![]() $\wedge ^{\dim \mathfrak {g}_{\bar 1}}(\mathfrak {g}_{\bar 1})$
.
$\wedge ^{\dim \mathfrak {g}_{\bar 1}}(\mathfrak {g}_{\bar 1})$
.
For any module M having a composition series, we will use
![]() $[M : L]$
to denote the Jordan-Hölder multiplicity of the simple module L in a composition series of M.
$[M : L]$
to denote the Jordan-Hölder multiplicity of the simple module L in a composition series of M.
2.3. BGG category
 ${\mathcal {O}}$
${\mathcal {O}}$
We denote by
![]() ${\mathcal {O}}$
the BGG category with respect to the triangular decomposition (1.1). Namely,
${\mathcal {O}}$
the BGG category with respect to the triangular decomposition (1.1). Namely,
![]() ${\mathcal {O}}$
consists of finitely-generated
${\mathcal {O}}$
consists of finitely-generated
![]() $\mathfrak {g}$
-modules that are semisimple over
$\mathfrak {g}$
-modules that are semisimple over
![]() $\mathfrak {h}$
and locally finite over
$\mathfrak {h}$
and locally finite over
![]() $\mathfrak n^+$
. We shall denote the corresponding BGG category of
$\mathfrak n^+$
. We shall denote the corresponding BGG category of
![]() $\mathfrak {g}_{\bar 0}$
-modules by
$\mathfrak {g}_{\bar 0}$
-modules by
![]() ${\mathcal {O}}_{\bar 0}$
. For
${\mathcal {O}}_{\bar 0}$
. For
![]() $\lambda \in \mathfrak {h}^\ast $
, we denote by
$\lambda \in \mathfrak {h}^\ast $
, we denote by
![]() $M(\lambda )$
the Verma module of
$M(\lambda )$
the Verma module of
![]() $\mathfrak {b}$
-highest weight
$\mathfrak {b}$
-highest weight
![]() $\lambda $
and by
$\lambda $
and by
![]() $L(\lambda )$
its unique simple quotient. Denote by
$L(\lambda )$
its unique simple quotient. Denote by
![]() $P(\lambda )$
the projective cover of
$P(\lambda )$
the projective cover of
![]() $L(\lambda )$
in
$L(\lambda )$
in
![]() ${\mathcal {O}}$
. We will use the
${\mathcal {O}}$
. We will use the
![]() $0$
-subscript convention to denote the respective objects in
$0$
-subscript convention to denote the respective objects in
![]() ${\mathcal {O}}_{\bar 0}$
(e.g.,
${\mathcal {O}}_{\bar 0}$
(e.g.,
![]() $P_0(\lambda )$
is the projective cover of
$P_0(\lambda )$
is the projective cover of
![]() $L_0(\lambda )$
in
$L_0(\lambda )$
in
![]() ${\mathcal {O}}_{\bar 0}$
).
${\mathcal {O}}_{\bar 0}$
).
Denote by
![]() ${\mathcal {O}}_{\mathbb Z}$
the integral BGG subcategory (i.e., the full subcategory of
${\mathcal {O}}_{\mathbb Z}$
the integral BGG subcategory (i.e., the full subcategory of
![]() ${\mathcal {O}}$
consisting of all modules having integral weight spaces).
${\mathcal {O}}$
consisting of all modules having integral weight spaces).
We denote by
![]() ${\mathcal {O}}(\mathfrak l_\zeta )$
the BGG category of
${\mathcal {O}}(\mathfrak l_\zeta )$
the BGG category of
![]() $\mathfrak l_\zeta $
-modules with respect to the Borel subalgebra
$\mathfrak l_\zeta $
-modules with respect to the Borel subalgebra
![]() $\mathfrak l_\zeta \cap \mathfrak b$
. Similarly, we shall use the
$\mathfrak l_\zeta \cap \mathfrak b$
. Similarly, we shall use the
![]() $\mathfrak l_\zeta $
-subscript to denote respective
$\mathfrak l_\zeta $
-subscript to denote respective
![]() $\mathfrak l_\zeta $
-modules (e.g., we define the Verma module
$\mathfrak l_\zeta $
-modules (e.g., we define the Verma module
![]() $M_{\mathfrak l_\zeta }(\lambda )$
and its simple quotient
$M_{\mathfrak l_\zeta }(\lambda )$
and its simple quotient
![]() $L_{\mathfrak l_\zeta }(\lambda )$
in the category
$L_{\mathfrak l_\zeta }(\lambda )$
in the category
![]() ${\mathcal {O}}(\mathfrak l_\zeta )$
). Denote by
${\mathcal {O}}(\mathfrak l_\zeta )$
). Denote by
![]() $P_{\mathfrak l_\zeta }(\lambda )$
the projective cover of
$P_{\mathfrak l_\zeta }(\lambda )$
the projective cover of
![]() $L_{\mathfrak l_\zeta }(\lambda )$
in
$L_{\mathfrak l_\zeta }(\lambda )$
in
![]() ${\mathcal {O}}(\mathfrak l_\zeta )$
. Similarly, we denote by
${\mathcal {O}}(\mathfrak l_\zeta )$
. Similarly, we denote by
![]() ${\mathcal {O}}(\mathfrak l_\zeta )_{\mathbb Z}$
the integral BGG subcategory of
${\mathcal {O}}(\mathfrak l_\zeta )_{\mathbb Z}$
the integral BGG subcategory of
![]() ${\mathcal {O}}(\mathfrak l_\zeta )$
.
${\mathcal {O}}(\mathfrak l_\zeta )$
.
2.4. The category
 ${\mathcal {O}}^{\zeta \text {-pres}}$
${\mathcal {O}}^{\zeta \text {-pres}}$
A projective module in
![]() ${\mathcal {O}}$
(respectively,
${\mathcal {O}}$
(respectively,
![]() ${\mathcal {O}}_{\bar 0}$
) is called admissible if any of its simple quotients are of the form
${\mathcal {O}}_{\bar 0}$
) is called admissible if any of its simple quotients are of the form
![]() $L(\lambda )$
(respectively,
$L(\lambda )$
(respectively,
![]() $L_0(\lambda )$
) with
$L_0(\lambda )$
) with
![]() $\lambda \in {\Lambda (\zeta )}$
. We denote by
$\lambda \in {\Lambda (\zeta )}$
. We denote by
![]() ${\mathcal {O}}^{\zeta \text {-pres}}$
the full subcategory of
${\mathcal {O}}^{\zeta \text {-pres}}$
the full subcategory of
![]() ${\mathcal {O}}_{\mathbb Z}$
consisting of modules M that have a two-step resolution of the form
${\mathcal {O}}_{\mathbb Z}$
consisting of modules M that have a two-step resolution of the form
where
![]() $P_1,P_2$
are admissible projective modules in
$P_1,P_2$
are admissible projective modules in
![]() ${\mathcal {O}}$
. Similarly, we define the full subcategory
${\mathcal {O}}$
. Similarly, we define the full subcategory
![]() ${\mathcal {O}}^{\zeta \text {-pres}}_{\bar 0}$
of
${\mathcal {O}}^{\zeta \text {-pres}}_{\bar 0}$
of
![]() ${\mathcal {O}}_{\bar 0}$
consisting of all modules that have
${\mathcal {O}}_{\bar 0}$
consisting of all modules that have
![]() $2$
-step resolutions by direct sums of projective modules of the form
$2$
-step resolutions by direct sums of projective modules of the form
![]() $P_0(\lambda )$
with
$P_0(\lambda )$
with
![]() $\lambda \in {\Lambda (\zeta )}$
.
$\lambda \in {\Lambda (\zeta )}$
.
Fix
![]() $\alpha \in \Pi _\zeta $
. A
$\alpha \in \Pi _\zeta $
. A
![]() $\mathfrak {g}$
-module M is said to be
$\mathfrak {g}$
-module M is said to be
![]() $\alpha $
-finite (respectively,
$\alpha $
-finite (respectively,
![]() $\alpha $
-free) if the action of non-zero root vectors in
$\alpha $
-free) if the action of non-zero root vectors in
![]() $\mathfrak {g}_{-\alpha }$
on M is locally finite (respectively, injective). For
$\mathfrak {g}_{-\alpha }$
on M is locally finite (respectively, injective). For
![]() $\alpha \in \Pi _\zeta $
, we have
$\alpha \in \Pi _\zeta $
, we have
![]() $(\lambda +\rho ,\alpha ^\vee )=(\lambda +\rho _{\mathfrak l_\zeta },\alpha ^\vee )=(\lambda +\rho _{\bar 0},\alpha ^\vee )$
, where
$(\lambda +\rho ,\alpha ^\vee )=(\lambda +\rho _{\mathfrak l_\zeta },\alpha ^\vee )=(\lambda +\rho _{\bar 0},\alpha ^\vee )$
, where
![]() $\rho _{\mathfrak l_\zeta }$
denotes the half-sum of positive roots in
$\rho _{\mathfrak l_\zeta }$
denotes the half-sum of positive roots in
![]() $\mathfrak l_\zeta $
, and hence,
$\mathfrak l_\zeta $
, and hence,
![]() $L(\lambda )$
is
$L(\lambda )$
is
![]() $\alpha $
-free if and only if
$\alpha $
-free if and only if
![]() $L_0(\lambda )$
is
$L_0(\lambda )$
is
![]() $\alpha $
-free if and only if
$\alpha $
-free if and only if
![]() $\lambda \in {\Lambda (\zeta )}$
, see, for example, [Reference Coulembier and MazorchukCM, Lemma 2.1].
$\lambda \in {\Lambda (\zeta )}$
, see, for example, [Reference Coulembier and MazorchukCM, Lemma 2.1].
Lemma 3. If
![]() $P(\lambda )$
is admissible, then
$P(\lambda )$
is admissible, then
![]() $\operatorname {Res}\nolimits P(\lambda )$
is admissible. Conversely, if
$\operatorname {Res}\nolimits P(\lambda )$
is admissible. Conversely, if
![]() $P_0(\lambda )$
is admissible, then
$P_0(\lambda )$
is admissible, then
![]() $\operatorname {Ind}\nolimits P_0(\lambda )$
is admissible. Thus, the functors
$\operatorname {Ind}\nolimits P_0(\lambda )$
is admissible. Thus, the functors
![]() $\operatorname {Ind}\nolimits (-)$
and
$\operatorname {Ind}\nolimits (-)$
and
![]() $\operatorname {Res}\nolimits (-)$
form an adjoint pair of additive functors between the full subcategories
$\operatorname {Res}\nolimits (-)$
form an adjoint pair of additive functors between the full subcategories
![]() ${\mathcal {O}}^{\zeta \text {-pres}}_{\bar 0}$
and
${\mathcal {O}}^{\zeta \text {-pres}}_{\bar 0}$
and
![]() ${\mathcal {O}}^{\zeta \text {-pres}}$
.
${\mathcal {O}}^{\zeta \text {-pres}}$
.
Proof. Suppose that
![]() $P(\lambda )$
is admissible. We have
$P(\lambda )$
is admissible. We have
![]() $0\not =\operatorname {Hom}\nolimits _{{\mathcal {O}}_{\bar 0}}(P_0(\lambda ),\operatorname {Res}\nolimits L(\lambda ))\cong \operatorname {Hom}\nolimits _{{\mathcal {O}}}(\operatorname {Ind}\nolimits P_0(\lambda ),L(\lambda ))$
, and hence
$0\not =\operatorname {Hom}\nolimits _{{\mathcal {O}}_{\bar 0}}(P_0(\lambda ),\operatorname {Res}\nolimits L(\lambda ))\cong \operatorname {Hom}\nolimits _{{\mathcal {O}}}(\operatorname {Ind}\nolimits P_0(\lambda ),L(\lambda ))$
, and hence
![]() $P(\lambda )$
is a direct summand of
$P(\lambda )$
is a direct summand of
![]() $\operatorname {Ind}\nolimits P_0(\lambda )$
. Since
$\operatorname {Ind}\nolimits P_0(\lambda )$
. Since
![]() $\operatorname {Res}\nolimits \operatorname {Ind}\nolimits P_0(\lambda )$
is admissible, so is
$\operatorname {Res}\nolimits \operatorname {Ind}\nolimits P_0(\lambda )$
is admissible, so is
![]() $\operatorname {Res}\nolimits P(\lambda )$
.
$\operatorname {Res}\nolimits P(\lambda )$
.
Conversely, suppose that
![]() $P_0(\lambda )$
is admissible. Now, if
$P_0(\lambda )$
is admissible. Now, if
![]() $\operatorname {Hom}\nolimits _{{\mathcal {O}}}(\operatorname {Ind}\nolimits P_0(\lambda ),L(\mu ))\not =0$
, then
$\operatorname {Hom}\nolimits _{{\mathcal {O}}}(\operatorname {Ind}\nolimits P_0(\lambda ),L(\mu ))\not =0$
, then
![]() $\operatorname {Hom}\nolimits _{{\mathcal {O}}_{\bar 0}}(P_0(\lambda ),\operatorname {Res}\nolimits L(\mu ))\not =0$
. Thus, there is a
$\operatorname {Hom}\nolimits _{{\mathcal {O}}_{\bar 0}}(P_0(\lambda ),\operatorname {Res}\nolimits L(\mu ))\not =0$
. Thus, there is a
![]() $\mathfrak {g}_{\bar 0}$
-composition factor in
$\mathfrak {g}_{\bar 0}$
-composition factor in
![]() $L(\mu )$
that is
$L(\mu )$
that is
![]() $\alpha $
-free, for all
$\alpha $
-free, for all
![]() $\alpha \in \Pi _\zeta $
. Since
$\alpha \in \Pi _\zeta $
. Since
![]() $L(\mu )$
is irreducible, this implies that it is also
$L(\mu )$
is irreducible, this implies that it is also
![]() $\alpha $
-free, for all
$\alpha $
-free, for all
![]() $\alpha \in \Pi _\zeta $
and so
$\alpha \in \Pi _\zeta $
and so
![]() $\mu \in \Lambda (\zeta )$
. Thus,
$\mu \in \Lambda (\zeta )$
. Thus,
![]() $\operatorname {Ind}\nolimits P_0(\lambda )$
is admissible.
$\operatorname {Ind}\nolimits P_0(\lambda )$
is admissible.
2.5. Serre quotient category
 ${\overline {{\mathcal {O}}}}$
${\overline {{\mathcal {O}}}}$
Let
![]() $\mathcal I_\zeta $
denote the Serre subcategory of
$\mathcal I_\zeta $
denote the Serre subcategory of
![]() ${\mathcal {O}}_{\mathbb Z}$
generated by simple modules
${\mathcal {O}}_{\mathbb Z}$
generated by simple modules
![]() $L(\lambda )$
with
$L(\lambda )$
with
![]() $\lambda \notin {\Lambda (\zeta )}$
; that is,
$\lambda \notin {\Lambda (\zeta )}$
; that is,
![]() $L(\lambda )\in {\mathcal {O}}_{\mathbb Z}$
is
$L(\lambda )\in {\mathcal {O}}_{\mathbb Z}$
is
![]() $\alpha $
-finite for some
$\alpha $
-finite for some
![]() $\alpha \in \Pi _\zeta $
. There is an associated abelian quotient category
$\alpha \in \Pi _\zeta $
. There is an associated abelian quotient category
![]() ${\overline {{\mathcal {O}}}}:={\mathcal {O}}_{\mathbb Z}/\mathcal I_\zeta $
in the sense of [Reference GabrielGa, Chapter III] which has the same objects as
${\overline {{\mathcal {O}}}}:={\mathcal {O}}_{\mathbb Z}/\mathcal I_\zeta $
in the sense of [Reference GabrielGa, Chapter III] which has the same objects as
![]() ${\mathcal {O}}_{\mathbb Z}$
and morphisms given by
${\mathcal {O}}_{\mathbb Z}$
and morphisms given by
where the limit is taken over all
![]() $X'\subseteq X$
and
$X'\subseteq X$
and
![]() $Y'\subseteq Y$
such that
$Y'\subseteq Y$
such that
![]() $X/X',Y'\in \mathcal I_\zeta $
. There is an exact canonical quotient functor
$X/X',Y'\in \mathcal I_\zeta $
. There is an exact canonical quotient functor
![]() $\pi :{\mathcal {O}}_{\mathbb Z}\rightarrow {\overline {{\mathcal {O}}}}$
, which is the identity on objects and is the canonical map from
$\pi :{\mathcal {O}}_{\mathbb Z}\rightarrow {\overline {{\mathcal {O}}}}$
, which is the identity on objects and is the canonical map from
![]() $\operatorname {Hom}\nolimits _{{\mathcal {O}}}(X,Y)$
to
$\operatorname {Hom}\nolimits _{{\mathcal {O}}}(X,Y)$
to
![]() $\lim \limits _{\rightarrow }\operatorname {Hom}\nolimits _{{\mathcal {O}}}(X',Y/Y')$
. We refer to
$\lim \limits _{\rightarrow }\operatorname {Hom}\nolimits _{{\mathcal {O}}}(X',Y/Y')$
. We refer to
![]() $\pi $
as the associated Serre quotient functor.
$\pi $
as the associated Serre quotient functor.
By [Reference Chen, Cheng and MazorchukCCM2, Lemma 12], the functor
![]() $\pi $
gives rise to an equivalence from
$\pi $
gives rise to an equivalence from
![]() $ {\mathcal {O}}^{{\zeta }\text {-pres}}$
to
$ {\mathcal {O}}^{{\zeta }\text {-pres}}$
to
![]() $\overline {{\mathcal {O}}}.$
In particular,
$\overline {{\mathcal {O}}}.$
In particular,
![]() ${\mathcal {O}}^{{\zeta }\text {-pres}}$
inherits an abelian category structure, and
${\mathcal {O}}^{{\zeta }\text {-pres}}$
inherits an abelian category structure, and
![]() $\{\pi (L(\lambda ))|~\lambda \in {\Lambda (\zeta )}\}$
is an exhaustive list of simple objects in
$\{\pi (L(\lambda ))|~\lambda \in {\Lambda (\zeta )}\}$
is an exhaustive list of simple objects in
![]() $\overline {{\mathcal {O}}}$
. Furthermore,
$\overline {{\mathcal {O}}}$
. Furthermore,
![]() $\pi (P(\lambda ))$
is the indecomposable projective cover of
$\pi (P(\lambda ))$
is the indecomposable projective cover of
![]() $\pi (L(\lambda ))$
in
$\pi (L(\lambda ))$
in
![]() $\overline {{\mathcal {O}}}$
, for any
$\overline {{\mathcal {O}}}$
, for any
![]() $\lambda \in {\Lambda (\zeta )}$
.
$\lambda \in {\Lambda (\zeta )}$
.
With respect to the inherited abelian category structure, the induced functors
![]() $\operatorname {Ind}\nolimits (-)$
and
$\operatorname {Ind}\nolimits (-)$
and
![]() $\operatorname {Res}\nolimits (-)$
between
$\operatorname {Res}\nolimits (-)$
between
![]() ${\mathcal {O}}^{\zeta \text {-pres}}_{\bar 0}$
and
${\mathcal {O}}^{\zeta \text {-pres}}_{\bar 0}$
and
![]() ${\mathcal {O}}^{\zeta \text {-pres}}$
are exact since
${\mathcal {O}}^{\zeta \text {-pres}}$
are exact since
![]() $\operatorname {Ind}\nolimits (-)$
is also right adjoint to
$\operatorname {Ind}\nolimits (-)$
is also right adjoint to
![]() $\operatorname {Res}\nolimits (-)$
, up to an auto-equivalence on
$\operatorname {Res}\nolimits (-)$
, up to an auto-equivalence on
![]() ${\mathcal {O}}^{\zeta \text {-pres}}_{\bar 0}$
.
${\mathcal {O}}^{\zeta \text {-pres}}_{\bar 0}$
.
2.6. The Whittaker category
 $\mathcal W(\zeta )$
$\mathcal W(\zeta )$
Let
![]() $\lambda \in \mathfrak {h}^\ast $
. We set
$\lambda \in \mathfrak {h}^\ast $
. We set
![]() $\chi _\lambda ^{\mathfrak l_\zeta }:Z(\mathfrak l_\zeta )\rightarrow {\mathbb {C}}$
to be the central character associated with
$\chi _\lambda ^{\mathfrak l_\zeta }:Z(\mathfrak l_\zeta )\rightarrow {\mathbb {C}}$
to be the central character associated with
![]() $\lambda $
. We recall from [Reference ChenCh1, Section 3.1] that the standard Whittaker module is defined as follows:
$\lambda $
. We recall from [Reference ChenCh1, Section 3.1] that the standard Whittaker module is defined as follows:
where
![]() $Y_\zeta (\lambda , \zeta ):=U(\mathfrak l_\zeta )/(\text {Ker}\chi _\lambda ^{\mathfrak l_\zeta }) U(\mathfrak l_\zeta )\otimes _{U({\mathfrak n^+}\cap \mathfrak l_\zeta )}{\mathbb {C}}_\zeta $
denotes Kostant’s simple Whittaker modules from [Reference KostantKo]. We denote by
$Y_\zeta (\lambda , \zeta ):=U(\mathfrak l_\zeta )/(\text {Ker}\chi _\lambda ^{\mathfrak l_\zeta }) U(\mathfrak l_\zeta )\otimes _{U({\mathfrak n^+}\cap \mathfrak l_\zeta )}{\mathbb {C}}_\zeta $
denotes Kostant’s simple Whittaker modules from [Reference KostantKo]. We denote by
![]() $L(\lambda ,\zeta )$
the (simple) top of
$L(\lambda ,\zeta )$
the (simple) top of
![]() $M(\lambda , \zeta )$
. Furthermore, we have
$M(\lambda , \zeta )$
. Furthermore, we have
for any
![]() $\mu \in \mathfrak {h}^\ast $
. We refer to [Reference ChenCh1, Theorem 6] for more details. In particular, we have
$\mu \in \mathfrak {h}^\ast $
. We refer to [Reference ChenCh1, Theorem 6] for more details. In particular, we have
![]() $M(\lambda ,0)=M(\lambda )$
. We denote by
$M(\lambda ,0)=M(\lambda )$
. We denote by
![]() $\mathcal N_0(\zeta )$
the corresponding Whittaker category of
$\mathcal N_0(\zeta )$
the corresponding Whittaker category of
![]() $\mathfrak {g}_{\bar 0}$
-modules and by
$\mathfrak {g}_{\bar 0}$
-modules and by
![]() $M_0(\lambda ,\zeta )$
the corresponding standard Whittaker module over
$M_0(\lambda ,\zeta )$
the corresponding standard Whittaker module over
![]() $\mathfrak {g}_{\bar 0}$
.
$\mathfrak {g}_{\bar 0}$
.
Recall that
![]() $\mathcal N(\zeta )$
denotes the category of finitely generated
$\mathcal N(\zeta )$
denotes the category of finitely generated
![]() $\mathfrak {g}$
-modules M that are locally finite over
$\mathfrak {g}$
-modules M that are locally finite over
![]() $Z(\mathfrak {g}_{\bar 0})$
and
$Z(\mathfrak {g}_{\bar 0})$
and
![]() $U(\mathfrak n^+)$
such that
$U(\mathfrak n^+)$
such that
![]() $x-\zeta (x)$
acts on M locally nilpotently, for any
$x-\zeta (x)$
acts on M locally nilpotently, for any
![]() $x\in \mathfrak n^+_{\bar 0}$
. The set
$x\in \mathfrak n^+_{\bar 0}$
. The set
![]() $\{{L}(\lambda , \zeta )|\lambda \in \mathfrak {h}^*/W_\zeta \}$
is a complete and nonredundant set of representatives of the isomorphism classes of simple objects in
$\{{L}(\lambda , \zeta )|\lambda \in \mathfrak {h}^*/W_\zeta \}$
is a complete and nonredundant set of representatives of the isomorphism classes of simple objects in
![]() ${\mathcal N}(\zeta )$
.
${\mathcal N}(\zeta )$
.
We consider the category
![]() $\mathcal W(\zeta )$
introduced in [Reference Chen, Cheng and MazorchukCCM2, Section 4.4.4], which is a deformation of the category
$\mathcal W(\zeta )$
introduced in [Reference Chen, Cheng and MazorchukCCM2, Section 4.4.4], which is a deformation of the category
![]() ${\mathcal {O}}$
and contains the modules
${\mathcal {O}}$
and contains the modules
![]() $M(\lambda ,\zeta )$
and
$M(\lambda ,\zeta )$
and
![]() $L(\lambda ,\zeta )$
for all
$L(\lambda ,\zeta )$
for all
![]() $\lambda \in \Lambda $
; see also [Reference ChenCh1, Theorem 16, Proposition 33]. The category
$\lambda \in \Lambda $
; see also [Reference ChenCh1, Theorem 16, Proposition 33]. The category
![]() $\mathcal W(\zeta )$
is defined as the full subcategory of
$\mathcal W(\zeta )$
is defined as the full subcategory of
![]() $\mathcal N(\zeta )$
consisting of modules M that have a two step resolution of modules of the form
$\mathcal N(\zeta )$
consisting of modules M that have a two step resolution of modules of the form
![]() $E\otimes \operatorname {Ind}\nolimits (M_0(\nu ,\zeta ))$
, where E is a finite-dimensional
$E\otimes \operatorname {Ind}\nolimits (M_0(\nu ,\zeta ))$
, where E is a finite-dimensional
![]() $\mathfrak {g}$
-module and
$\mathfrak {g}$
-module and
![]() $\nu $
is a dominant (i.e.,
$\nu $
is a dominant (i.e.,
![]() $\nu $
is
$\nu $
is
![]() $\alpha $
-dominant for any
$\alpha $
-dominant for any
![]() $\alpha \in \Phi _{\bar 0}^+$
) and integral weight such that its stabilizer subgroup of W under the dot-action is equal to
$\alpha \in \Phi _{\bar 0}^+$
) and integral weight such that its stabilizer subgroup of W under the dot-action is equal to
![]() $W_\zeta $
.
$W_\zeta $
.
Let us conclude this section with some remarks on equivalences of categories. There is an equivalence between
![]() ${\mathcal {O}}^{\zeta \text {-pres}}$
and
${\mathcal {O}}^{\zeta \text {-pres}}$
and
![]() $\mathcal W(\zeta )$
; see Section 7.1. As a consequence, we have equivalences
$\mathcal W(\zeta )$
; see Section 7.1. As a consequence, we have equivalences
![]() ${\mathcal {O}}^{\zeta \text {-pres}}\cong \mathcal W(\zeta )\cong {\overline {{\mathcal {O}}}}$
. In the case that
${\mathcal {O}}^{\zeta \text {-pres}}\cong \mathcal W(\zeta )\cong {\overline {{\mathcal {O}}}}$
. In the case that
![]() $\mathfrak {g}$
is one from Kac’s list (1.2), a description of objects in
$\mathfrak {g}$
is one from Kac’s list (1.2), a description of objects in
![]() ${\mathcal {O}}^{\zeta \text {-pres}}$
and
${\mathcal {O}}^{\zeta \text {-pres}}$
and
![]() ${\overline {{\mathcal {O}}}}$
corresponding to Whittaker modules
${\overline {{\mathcal {O}}}}$
corresponding to Whittaker modules
![]() $M(\lambda ,\zeta )$
and
$M(\lambda ,\zeta )$
and
![]() $L(\lambda ,\zeta )$
can be found in Remark 30.
$L(\lambda ,\zeta )$
can be found in Remark 30.
3. Proof of Theorem 1
In this section, we give a proof of Theorem 1.
3.1. Backelin functor
 $\Gamma _\zeta $
$\Gamma _\zeta $
Recall that the image
![]() $\Gamma _\zeta (M)$
of the exact Backelin functor
$\Gamma _\zeta (M)$
of the exact Backelin functor
![]() $\Gamma _\zeta :{\mathcal {O}}\rightarrow \mathcal N(\zeta )$
on a module
$\Gamma _\zeta :{\mathcal {O}}\rightarrow \mathcal N(\zeta )$
on a module
![]() $M\in {\mathcal {O}}$
is defined as the submodule consisting of vectors in
$M\in {\mathcal {O}}$
is defined as the submodule consisting of vectors in
![]() $\overline M:=\prod _{\lambda \in \mathfrak h^\ast } M_\lambda $
annihilated by a power of
$\overline M:=\prod _{\lambda \in \mathfrak h^\ast } M_\lambda $
annihilated by a power of
![]() $x-\zeta (x)$
, for all
$x-\zeta (x)$
, for all
![]() $x\in \mathfrak n^+_{\bar 0}$
. Let
$x\in \mathfrak n^+_{\bar 0}$
. Let
![]() $\Gamma _\zeta ^0:{\mathcal {O}}_{\bar 0}\rightarrow \mathcal N_0(\zeta )$
denote the Backelin functor for
$\Gamma _\zeta ^0:{\mathcal {O}}_{\bar 0}\rightarrow \mathcal N_0(\zeta )$
denote the Backelin functor for
![]() $\mathfrak {g}_{\bar 0}$
-modules from [Reference BackelinBac]. Similarly, we denote by
$\mathfrak {g}_{\bar 0}$
-modules from [Reference BackelinBac]. Similarly, we denote by
![]() $\Gamma _\zeta ^{\mathfrak l_\zeta }$
the Backelin functor for
$\Gamma _\zeta ^{\mathfrak l_\zeta }$
the Backelin functor for
![]() $\mathfrak l_\zeta $
-modules. We note that
$\mathfrak l_\zeta $
-modules. We note that
![]() $\operatorname {Res}\nolimits (-)$
intertwines
$\operatorname {Res}\nolimits (-)$
intertwines
![]() $\Gamma _\zeta $
and
$\Gamma _\zeta $
and
![]() $\Gamma ^0_\zeta $
. The following proposition is crucial.
$\Gamma ^0_\zeta $
. The following proposition is crucial.
Proposition 4. For any
![]() $\lambda \in \mathfrak {h}^*$
, we have
$\lambda \in \mathfrak {h}^*$
, we have
In particular, for any
![]() $w\in W_\zeta $
, we have
$w\in W_\zeta $
, we have
Proof. By the PBW basis theorem, we may regard
![]() $\overline {M(\lambda )}$
as the vector space
$\overline {M(\lambda )}$
as the vector space
![]() $U(\mathfrak u^-_{\bar 1})\otimes \overline {U(\mathfrak u^-_{\bar 0})M_{\mathfrak l_\zeta }(\lambda )}=U(\mathfrak u^-_{\bar 1})\otimes \overline {M_0(\lambda )}.$
Therefore,
$U(\mathfrak u^-_{\bar 1})\otimes \overline {U(\mathfrak u^-_{\bar 0})M_{\mathfrak l_\zeta }(\lambda )}=U(\mathfrak u^-_{\bar 1})\otimes \overline {M_0(\lambda )}.$
Therefore,
![]() $\Gamma _\zeta (M(\lambda ))$
consists of vectors v in
$\Gamma _\zeta (M(\lambda ))$
consists of vectors v in
![]() $U(\mathfrak u^-_{\bar 1})\otimes \overline {M_0(\lambda )}$
such that
$U(\mathfrak u^-_{\bar 1})\otimes \overline {M_0(\lambda )}$
such that
![]() $x-\zeta (x)$
acts nilpotently on v, for each
$x-\zeta (x)$
acts nilpotently on v, for each
![]() $x\in \mathfrak n^+_{\bar 0}$
. There is an embedding
$x\in \mathfrak n^+_{\bar 0}$
. There is an embedding
![]() $U(\mathfrak u^-_{\bar 1})\otimes \Gamma ^0_\zeta (M_0(\lambda ))\hookrightarrow \Gamma _\zeta (M(\lambda ))$
induced by the inclusion
$U(\mathfrak u^-_{\bar 1})\otimes \Gamma ^0_\zeta (M_0(\lambda ))\hookrightarrow \Gamma _\zeta (M(\lambda ))$
induced by the inclusion
![]() $\Gamma ^0_\zeta (M_0(\lambda ))\hookrightarrow \overline {M_0(\lambda )}$
. Now by [Reference BackelinBac, Proposition 6.9], one has
$\Gamma ^0_\zeta (M_0(\lambda ))\hookrightarrow \overline {M_0(\lambda )}$
. Now by [Reference BackelinBac, Proposition 6.9], one has
![]() $\Gamma ^0_\zeta (M_0(\lambda ))=M_0(\lambda ,\zeta )$
, and hence, we get an inclusion
$\Gamma ^0_\zeta (M_0(\lambda ))=M_0(\lambda ,\zeta )$
, and hence, we get an inclusion
such that
![]() $U(\mathfrak u^-_{\bar 1})X= U(\mathfrak u^-_{\bar 1})\otimes X$
, where
$U(\mathfrak u^-_{\bar 1})X= U(\mathfrak u^-_{\bar 1})\otimes X$
, where
![]() $X\subset \overline {M_0(\lambda )}$
is a
$X\subset \overline {M_0(\lambda )}$
is a
![]() $\mathfrak {g}_{\bar 0}$
-submodule isomorphic to
$\mathfrak {g}_{\bar 0}$
-submodule isomorphic to
![]() $M_0(\lambda ,\zeta )$
.
$M_0(\lambda ,\zeta )$
.
We claim that the inclusion (3.2) is an equality. We can argue as follows: For
![]() $M\in \mathcal N(\zeta )$
, we have
$M\in \mathcal N(\zeta )$
, we have
![]() $\operatorname {Res}\nolimits ^{\mathfrak {g}}_{\mathfrak l_\zeta }\Gamma _\zeta (M)=\Gamma ^{\mathfrak l_\zeta }_\zeta \operatorname {Res}\nolimits ^{\mathfrak {g}}_{\mathfrak l_\zeta }(M)$
. For
$\operatorname {Res}\nolimits ^{\mathfrak {g}}_{\mathfrak l_\zeta }\Gamma _\zeta (M)=\Gamma ^{\mathfrak l_\zeta }_\zeta \operatorname {Res}\nolimits ^{\mathfrak {g}}_{\mathfrak l_\zeta }(M)$
. For
![]() $\lambda \in \mathfrak {h}^*$
, we now compute
$\lambda \in \mathfrak {h}^*$
, we now compute
 $$ \begin{align*} \operatorname{Res}\nolimits^{\mathfrak{g}}_{\mathfrak l_\zeta}\Gamma_\zeta(M(\lambda))=& \operatorname{Res}\nolimits^{\mathfrak{g}}_{\mathfrak l_\zeta}\Gamma_\zeta(U(\mathfrak u^-)\otimes M_{\mathfrak l_\zeta}(\lambda)) = \operatorname{Res}\nolimits^{\mathfrak{g}}_{\mathfrak l_\zeta}U(\mathfrak u^-)\otimes \Gamma^{\mathfrak l_\zeta}_\zeta(M_{\mathfrak l_\zeta}(\lambda))\\ =& \operatorname{Res}\nolimits^{\mathfrak{g}}_{\mathfrak l_\zeta}U(\mathfrak u^-)\otimes M_{\mathfrak l_\zeta}(\lambda,\zeta) = \operatorname{Res}\nolimits^{\mathfrak{g}}_{\mathfrak l_\zeta}M(\lambda,\zeta). \end{align*} $$
$$ \begin{align*} \operatorname{Res}\nolimits^{\mathfrak{g}}_{\mathfrak l_\zeta}\Gamma_\zeta(M(\lambda))=& \operatorname{Res}\nolimits^{\mathfrak{g}}_{\mathfrak l_\zeta}\Gamma_\zeta(U(\mathfrak u^-)\otimes M_{\mathfrak l_\zeta}(\lambda)) = \operatorname{Res}\nolimits^{\mathfrak{g}}_{\mathfrak l_\zeta}U(\mathfrak u^-)\otimes \Gamma^{\mathfrak l_\zeta}_\zeta(M_{\mathfrak l_\zeta}(\lambda))\\ =& \operatorname{Res}\nolimits^{\mathfrak{g}}_{\mathfrak l_\zeta}U(\mathfrak u^-)\otimes M_{\mathfrak l_\zeta}(\lambda,\zeta) = \operatorname{Res}\nolimits^{\mathfrak{g}}_{\mathfrak l_\zeta}M(\lambda,\zeta). \end{align*} $$
The third identity above follows from [Reference Miličić and SoergelMSo, Lemma 5.12] and the fact that
![]() $U(\mathfrak u^-)$
is a weight module and at the same time a direct sum of finite-dimensional irreducible
$U(\mathfrak u^-)$
is a weight module and at the same time a direct sum of finite-dimensional irreducible
![]() $\mathfrak l_\zeta $
-modules. Thus, we conclude that
$\mathfrak l_\zeta $
-modules. Thus, we conclude that
![]() $U(\mathfrak u^-_{\bar 1})X \hookrightarrow \Gamma _{\zeta }(M(\lambda ))$
is an isomorphism.
$U(\mathfrak u^-_{\bar 1})X \hookrightarrow \Gamma _{\zeta }(M(\lambda ))$
is an isomorphism.
We also provide an alternative proof of the subjectivity of the inclusion in (3.2) as follows. For any
![]() $M\in \mathcal N(\zeta )$
and
$M\in \mathcal N(\zeta )$
and
![]() $c\in {\mathbb {C}}$
, with respect to the operator H from (1.4), we denote by
$c\in {\mathbb {C}}$
, with respect to the operator H from (1.4), we denote by
![]() $M_c$
the generalized eigenspace of M, which lies in
$M_c$
the generalized eigenspace of M, which lies in
![]() $\mathcal N_{\mathfrak l_\zeta }$
and so has finite length as an
$\mathcal N_{\mathfrak l_\zeta }$
and so has finite length as an
![]() $\mathfrak l_\zeta $
-module. We note that
$\mathfrak l_\zeta $
-module. We note that
![]() $U(\mathfrak u^-_{\bar 1})X\hookrightarrow \Gamma _\zeta (M(\lambda ))$
is surjective if and only if the
$U(\mathfrak u^-_{\bar 1})X\hookrightarrow \Gamma _\zeta (M(\lambda ))$
is surjective if and only if the
![]() $\mathfrak l_\zeta $
-modules
$\mathfrak l_\zeta $
-modules
![]() $(U(\mathfrak u^-_{\bar 1})X)_c$
and
$(U(\mathfrak u^-_{\bar 1})X)_c$
and
![]() $ \Gamma _\zeta (M(\lambda ))_c$
have the same composition factors for any
$ \Gamma _\zeta (M(\lambda ))_c$
have the same composition factors for any
![]() $c\in {\mathbb {C}}$
. Recall that
$c\in {\mathbb {C}}$
. Recall that
![]() $\operatorname {Res}\nolimits M(\lambda )$
has filtration subquotients of which are isomorphic to
$\operatorname {Res}\nolimits M(\lambda )$
has filtration subquotients of which are isomorphic to
![]() $M_{\bar 0}(\lambda +\gamma )$
with
$M_{\bar 0}(\lambda +\gamma )$
with
![]() $\gamma \in \Phi (\wedge (\mathfrak u^-_{\bar 1}))$
. Here,
$\gamma \in \Phi (\wedge (\mathfrak u^-_{\bar 1}))$
. Here,
![]() $\gamma \in \Phi (\wedge (\mathfrak u^-_{\bar 1}))$
denotes the set of roots in the space
$\gamma \in \Phi (\wedge (\mathfrak u^-_{\bar 1}))$
denotes the set of roots in the space
![]() $\wedge (\mathfrak u^-_{\bar 1})$
. Also, for any finite-dimensional weight module E over
$\wedge (\mathfrak u^-_{\bar 1})$
. Also, for any finite-dimensional weight module E over
![]() $\mathfrak l_\zeta $
, the tensor product
$\mathfrak l_\zeta $
, the tensor product
![]() $E\otimes Y_\zeta (\lambda ,\zeta )$
has filtration subquotients of which are
$E\otimes Y_\zeta (\lambda ,\zeta )$
has filtration subquotients of which are
![]() $Y_\zeta (\lambda +\gamma ,\zeta )$
with
$Y_\zeta (\lambda +\gamma ,\zeta )$
with
![]() $\gamma $
being weights of E by [Reference Miličić and SoergelMSo, Lemma 5.12]. Since the restriction functor intertwines
$\gamma $
being weights of E by [Reference Miličić and SoergelMSo, Lemma 5.12]. Since the restriction functor intertwines
![]() $\Gamma _\zeta $
and
$\Gamma _\zeta $
and
![]() $\Gamma _\zeta ^0$
, it follows that the
$\Gamma _\zeta ^0$
, it follows that the
![]() $\mathfrak l_\zeta $
-modules
$\mathfrak l_\zeta $
-modules
![]() $\Gamma _\zeta M(\lambda )_c$
,
$\Gamma _\zeta M(\lambda )_c$
,
![]() $(U(\mathfrak u^-_{\bar 0})\otimes U(\mathfrak u^-_{\bar 1})\otimes Y_\zeta (\lambda ,\mathfrak l_\zeta ))_c$
and
$(U(\mathfrak u^-_{\bar 0})\otimes U(\mathfrak u^-_{\bar 1})\otimes Y_\zeta (\lambda ,\mathfrak l_\zeta ))_c$
and
![]() $M(\lambda ,\zeta )_c$
have the same composition factors. As a consequence,
$M(\lambda ,\zeta )_c$
have the same composition factors. As a consequence,
![]() $(U(\mathfrak u^-_{\bar 1})X)_c$
and
$(U(\mathfrak u^-_{\bar 1})X)_c$
and
![]() $\Gamma _\zeta (M(\lambda ))_c$
have the same composition factors for any
$\Gamma _\zeta (M(\lambda ))_c$
have the same composition factors for any
![]() $c\in {\mathbb {C}}$
.
$c\in {\mathbb {C}}$
.
Recall again
![]() $H\in \mathfrak {h}$
from the parabolic decomposition (1.4). Since the inclusion in (3.2) is an equality, it follows that H acts on
$H\in \mathfrak {h}$
from the parabolic decomposition (1.4). Since the inclusion in (3.2) is an equality, it follows that H acts on
![]() $U(\mathfrak u_{\bar 1}^-)X=\Gamma _\zeta (M(\lambda ))$
semisimply with the highest eigenvalue
$U(\mathfrak u_{\bar 1}^-)X=\Gamma _\zeta (M(\lambda ))$
semisimply with the highest eigenvalue
![]() $\chi _{\lambda }^{\mathfrak l_\zeta }(H)$
. Let
$\chi _{\lambda }^{\mathfrak l_\zeta }(H)$
. Let
![]() $V\subseteq \operatorname {Res}\nolimits _{\mathfrak l_\zeta }^{\mathfrak {g}_{\bar 0}} X$
isomorphic to
$V\subseteq \operatorname {Res}\nolimits _{\mathfrak l_\zeta }^{\mathfrak {g}_{\bar 0}} X$
isomorphic to
![]() $Y_\zeta (\lambda ,\zeta )$
, which is the
$Y_\zeta (\lambda ,\zeta )$
, which is the
![]() $\chi _\lambda ^{\mathfrak l_\zeta }(H)$
-eigenspace in
$\chi _\lambda ^{\mathfrak l_\zeta }(H)$
-eigenspace in
![]() $\Gamma _\zeta (M(\lambda ))$
. Then
$\Gamma _\zeta (M(\lambda ))$
. Then
![]() $\mathfrak u^+ V =0$
. Thus, by Frobenius reciprocity, we have an isomorphism
$\mathfrak u^+ V =0$
. Thus, by Frobenius reciprocity, we have an isomorphism
![]() $M(\lambda ,\zeta )$
to
$M(\lambda ,\zeta )$
to
![]() $\Gamma _\zeta (M(\lambda ))$
. The conclusion follows.
$\Gamma _\zeta (M(\lambda ))$
. The conclusion follows.
3.2. Proof of Theorem 1
For a given
![]() $\mathfrak {g}$
-module M, we denote the subspace of Whittaker vectors associated to
$\mathfrak {g}$
-module M, we denote the subspace of Whittaker vectors associated to
![]() $\zeta $
by
$\zeta $
by
![]() $Wh_\zeta (M)$
– namely,
$Wh_\zeta (M)$
– namely,
We have the following generalization of [Reference Batra and MazorchukBM, Lemma 37] to quasi-reductive Lie superalgebras with a similar proof.
Lemma 5. Let M be either
![]() $N(-\mu )^{\ast }$
or
$N(-\mu )^{\ast }$
or
![]() $M(\mu )^{\ast ,\tau }$
. Then
$M(\mu )^{\ast ,\tau }$
. Then
![]() $\dim Wh_\zeta (M) =1$
.
$\dim Wh_\zeta (M) =1$
.
Proof. We observe that
![]() $N(-\mu )^*$
as an
$N(-\mu )^*$
as an
![]() $U(\mathfrak n^+)$
-module is isomorphic to the (full) dual
$U(\mathfrak n^+)$
-module is isomorphic to the (full) dual
![]() $U(\mathfrak n^+)^*$
, which in turn can be identified with the space of linear functions on
$U(\mathfrak n^+)^*$
, which in turn can be identified with the space of linear functions on
![]() $U(\mathfrak n^+)$
. The
$U(\mathfrak n^+)$
. The
![]() $\mathfrak n^+$
-character
$\mathfrak n^+$
-character
![]() $\zeta $
determines a unique linear function of
$\zeta $
determines a unique linear function of
![]() $U(\mathfrak n^+)$
, and hence, the Whittaker vectors corresponding to
$U(\mathfrak n^+)$
, and hence, the Whittaker vectors corresponding to
![]() $\zeta $
form a one-dimensional subspace in
$\zeta $
form a one-dimensional subspace in
![]() $N(-\mu )^*$
. The argument for
$N(-\mu )^*$
. The argument for
![]() $M(\mu )^{\ast ,\tau }$
is analogous.
$M(\mu )^{\ast ,\tau }$
is analogous.
A weight is called
![]() $W_\zeta $
-anti-dominant if it is
$W_\zeta $
-anti-dominant if it is
![]() $\alpha $
-anti-dominant for any root
$\alpha $
-anti-dominant for any root
![]() $\alpha $
in
$\alpha $
in
![]() $\mathfrak l_\zeta \cap \mathfrak {n}^+$
. The following theorem completes the proof of Theorem 1 and determines homomorphisms from standard Whittaker modules to the full dual of Verma modules:
$\mathfrak l_\zeta \cap \mathfrak {n}^+$
. The following theorem completes the proof of Theorem 1 and determines homomorphisms from standard Whittaker modules to the full dual of Verma modules:
Theorem 6. For any
![]() $\lambda , \mu \in \mathfrak {h}^\ast $
, we have
$\lambda , \mu \in \mathfrak {h}^\ast $
, we have
-
(i) For
 $M = N(-\mu )^\ast $
or
$M = N(-\mu )^\ast $
or
 $M(\mu )^{\ast ,\tau }$
,
$M(\mu )^{\ast ,\tau }$
,
 $\operatorname {Hom}\nolimits _{\mathfrak {g}}(M(\lambda ,\zeta ), M)= \left \{\begin {array}{ll} {\mathbb {C}}, & \text {~for } \lambda \in W_\zeta \cdot \mu ;\\ 0, & \text { otherwise}; \end {array} \right. $
$\operatorname {Hom}\nolimits _{\mathfrak {g}}(M(\lambda ,\zeta ), M)= \left \{\begin {array}{ll} {\mathbb {C}}, & \text {~for } \lambda \in W_\zeta \cdot \mu ;\\ 0, & \text { otherwise}; \end {array} \right. $
-
(ii)
 $\Gamma _\zeta (L(\lambda ))= \left \{\begin {array}{ll} L(\lambda ,\zeta ), & \text {~if}\ \lambda\ is\ W_\zeta\text{-}anti\text{-}dominant;\\ 0, & \text { otherwise}; \end {array} \right.$
$\Gamma _\zeta (L(\lambda ))= \left \{\begin {array}{ll} L(\lambda ,\zeta ), & \text {~if}\ \lambda\ is\ W_\zeta\text{-}anti\text{-}dominant;\\ 0, & \text { otherwise}; \end {array} \right.$
-
(iii)
 $\dim Wh_\zeta (L(\lambda ,\zeta )) =1.$
$\dim Wh_\zeta (L(\lambda ,\zeta )) =1.$
Proof. With Proposition 4 at our disposal, we can now follow the strategy of the proof of [Reference ChenCh1, Theorem 20]. We shall prove Part (i) for the case when
![]() $M = N(-\mu )^\ast $
. The case when
$M = N(-\mu )^\ast $
. The case when
![]() $M = M(\mu )^{\ast ,\tau }$
can be proved in a similar fashion.
$M = M(\mu )^{\ast ,\tau }$
can be proved in a similar fashion.
Since
![]() $Wh_\zeta (N(-\mu )^\ast ) \cong {\mathbb {C}}$
by Lemma 5, there exists a unique (up to a scalar) Whittaker vector corresponding to
$Wh_\zeta (N(-\mu )^\ast ) \cong {\mathbb {C}}$
by Lemma 5, there exists a unique (up to a scalar) Whittaker vector corresponding to
![]() $\zeta $
in
$\zeta $
in
![]() $N(-\mu )^*$
. Now, if
$N(-\mu )^*$
. Now, if
![]() $\mu \in W_\zeta \cdot \lambda $
, then we can define a nonzero
$\mu \in W_\zeta \cdot \lambda $
, then we can define a nonzero
![]() $\mathfrak l_\zeta $
-homomorphism from
$\mathfrak l_\zeta $
-homomorphism from
![]() $M_{\mathfrak l_\zeta }(\lambda ,\zeta )$
to
$M_{\mathfrak l_\zeta }(\lambda ,\zeta )$
to
![]() $N(-\mu )^*$
by sending a nonzero Whittaker vector of
$N(-\mu )^*$
by sending a nonzero Whittaker vector of
![]() $M_{\mathfrak l_\zeta }(\lambda ,\zeta )$
to a nonzero scalar multiple of the Whittaker vector of
$M_{\mathfrak l_\zeta }(\lambda ,\zeta )$
to a nonzero scalar multiple of the Whittaker vector of
![]() $N(-\mu )^*$
corresponding to
$N(-\mu )^*$
corresponding to
![]() $\zeta $
. Since
$\zeta $
. Since
![]() $\mathfrak u^+$
annihilates the Whittaker vector in
$\mathfrak u^+$
annihilates the Whittaker vector in
![]() $N(-\mu )^*$
, this map induces a
$N(-\mu )^*$
, this map induces a
![]() $\mathfrak {g}$
-homomorphism from
$\mathfrak {g}$
-homomorphism from
![]() $M(\lambda ,\zeta )$
to
$M(\lambda ,\zeta )$
to
![]() $N(-\mu )^*$
. By Lemma 5 again, it follows that
$N(-\mu )^*$
. By Lemma 5 again, it follows that
![]() $\operatorname {Hom}\nolimits _{\mathfrak {g}}(M(\lambda ,\zeta ), N(-\mu )^\ast )\cong {\mathbb {C}}$
. However, if
$\operatorname {Hom}\nolimits _{\mathfrak {g}}(M(\lambda ,\zeta ), N(-\mu )^\ast )\cong {\mathbb {C}}$
. However, if
![]() $\mu \not \in W_\zeta \cdot \lambda $
, then there exists
$\mu \not \in W_\zeta \cdot \lambda $
, then there exists
![]() $z\in Z(\mathfrak {g}_{\bar 0})$
that acts on the generating Whittaker vectors of
$z\in Z(\mathfrak {g}_{\bar 0})$
that acts on the generating Whittaker vectors of
![]() $M(\lambda ,\zeta )$
and
$M(\lambda ,\zeta )$
and
![]() $N(-\mu )^*$
with different scalars. Hence, in this case, we have
$N(-\mu )^*$
with different scalars. Hence, in this case, we have
![]() $\operatorname {Hom}\nolimits _{\mathfrak {g}}(M(\lambda ,\zeta ), N(-\mu )^\ast )=0$
. This proves Part (i).
$\operatorname {Hom}\nolimits _{\mathfrak {g}}(M(\lambda ,\zeta ), N(-\mu )^\ast )=0$
. This proves Part (i).
Since
![]() $\mu $
is a highest weight of
$\mu $
is a highest weight of
![]() $N(-\mu )^\ast $
, we get a nonzero homomorphism
$N(-\mu )^\ast $
, we get a nonzero homomorphism
![]() $f: M(\mu )\rightarrow N(-\mu )^\ast $
. Let
$f: M(\mu )\rightarrow N(-\mu )^\ast $
. Let
![]() $S\subseteq N(-\mu )^\ast $
be the image of f. We note that
$S\subseteq N(-\mu )^\ast $
be the image of f. We note that
![]() $\overline S\subset N(-\mu )^\ast $
and so
$\overline S\subset N(-\mu )^\ast $
and so
![]() $\Gamma _\zeta (S)$
can be regarded as a
$\Gamma _\zeta (S)$
can be regarded as a
![]() $\mathfrak {g}$
-submodule of
$\mathfrak {g}$
-submodule of
![]() $N(-\mu )^\ast $
. Since
$N(-\mu )^\ast $
. Since
![]() $\Gamma _\zeta (-)$
is exact, we get an epimorphism from
$\Gamma _\zeta (-)$
is exact, we get an epimorphism from
![]() $M(\mu ,\zeta )$
to
$M(\mu ,\zeta )$
to
![]() $\Gamma _\zeta (S)\subset N(-\mu )^\ast $
by Proposition 4. Now, the module
$\Gamma _\zeta (S)\subset N(-\mu )^\ast $
by Proposition 4. Now, the module
![]() $\Gamma _\zeta (S)$
is generated by a Whittaker vector since it is a quotient of
$\Gamma _\zeta (S)$
is generated by a Whittaker vector since it is a quotient of
![]() $\Gamma _\zeta (M(\mu ))\cong M(\mu ,\zeta )$
by Proposition 4. By Lemma 5, we have
$\Gamma _\zeta (M(\mu ))\cong M(\mu ,\zeta )$
by Proposition 4. By Lemma 5, we have
![]() $Wh_\zeta (\Gamma _\zeta (S))\cong {\mathbb {C}}$
which implies that
$Wh_\zeta (\Gamma _\zeta (S))\cong {\mathbb {C}}$
which implies that
![]() $\Gamma _\zeta (S)$
is simple, and hence,
$\Gamma _\zeta (S)$
is simple, and hence,
![]() $\Gamma _\zeta (S)\cong L(\mu ,\zeta )$
.
$\Gamma _\zeta (S)\cong L(\mu ,\zeta )$
.
The exactness of
![]() $\Gamma _\zeta $
together with the fact that
$\Gamma _\zeta $
together with the fact that
![]() $\Gamma _\zeta $
sends a quotient of
$\Gamma _\zeta $
sends a quotient of
![]() $M(\lambda )$
to
$M(\lambda )$
to
![]() $L(\lambda ,\zeta )$
implies that either
$L(\lambda ,\zeta )$
implies that either
![]() $\Gamma _\zeta (L(\lambda ))\cong 0$
or
$\Gamma _\zeta (L(\lambda ))\cong 0$
or
![]() $\Gamma _\zeta (L(\lambda ))\cong L(\lambda ,\zeta )$
. Now, if
$\Gamma _\zeta (L(\lambda ))\cong L(\lambda ,\zeta )$
. Now, if
![]() $\lambda $
is
$\lambda $
is
![]() $W_\zeta $
-anti-dominant, then
$W_\zeta $
-anti-dominant, then
![]() $\operatorname {Res}\nolimits \Gamma _\zeta (L(\lambda )) = \Gamma _\zeta ^0(\operatorname {Res}\nolimits L(\lambda )) \neq 0$
since
$\operatorname {Res}\nolimits \Gamma _\zeta (L(\lambda )) = \Gamma _\zeta ^0(\operatorname {Res}\nolimits L(\lambda )) \neq 0$
since
![]() $\operatorname {Res}\nolimits L(\lambda )$
has a composition factor isomorphic to
$\operatorname {Res}\nolimits L(\lambda )$
has a composition factor isomorphic to
![]() $L_0(\lambda )$
. If
$L_0(\lambda )$
. If
![]() $\lambda $
is not
$\lambda $
is not
![]() $W_\zeta $
-anti-dominant, then there is a
$W_\zeta $
-anti-dominant, then there is a
![]() $W_\zeta $
-anti-dominant weight
$W_\zeta $
-anti-dominant weight
![]() $\lambda '\in W_\zeta \cdot \lambda $
such that
$\lambda '\in W_\zeta \cdot \lambda $
such that
![]() $M_{\mathfrak l_\zeta }(\lambda ')\subseteq M_{\mathfrak l_\zeta }(\lambda )$
. Using parabolic induction, we have
$M_{\mathfrak l_\zeta }(\lambda ')\subseteq M_{\mathfrak l_\zeta }(\lambda )$
. Using parabolic induction, we have
![]() $M(\lambda ')\subseteq M(\lambda )$
. Also, we have
$M(\lambda ')\subseteq M(\lambda )$
. Also, we have
![]() $\Gamma _\zeta (M(\lambda ')=\Gamma _\zeta (M(\lambda ))$
by Proposition 4. As
$\Gamma _\zeta (M(\lambda ')=\Gamma _\zeta (M(\lambda ))$
by Proposition 4. As
![]() $L(\lambda )$
is a composition factor of
$L(\lambda )$
is a composition factor of
![]() $M(\lambda )/M(\lambda ')$
, this implies that
$M(\lambda )/M(\lambda ')$
, this implies that
![]() $\Gamma _\zeta (L(\lambda ))=0$
, and so Part (ii) follows.
$\Gamma _\zeta (L(\lambda ))=0$
, and so Part (ii) follows.
Part (iii) follows from the isomorphism
![]() $L(\mu ,\zeta )\cong \Gamma _\zeta (S)$
.
$L(\mu ,\zeta )\cong \Gamma _\zeta (S)$
.
4. Stratified structure of
 ${\mathcal {O}}^{\zeta \text {-} {pres}}$
${\mathcal {O}}^{\zeta \text {-} {pres}}$
In this section, we show that the category
![]() ${\mathcal {O}}^{\zeta \text {-pres}}$
admits a properly stratified structure in the sense of [Reference DlabDl, Reference Mazorchuk and StroppelMSt]. This extends the results in [Reference Chen, Cheng and MazorchukCCM2, Section 5], where the case of type I Lie superalgebras was considered.
${\mathcal {O}}^{\zeta \text {-pres}}$
admits a properly stratified structure in the sense of [Reference DlabDl, Reference Mazorchuk and StroppelMSt]. This extends the results in [Reference Chen, Cheng and MazorchukCCM2, Section 5], where the case of type I Lie superalgebras was considered.
4.1. Relation with the category
 ${\mathcal {O}}(\mathfrak l_\zeta )$
${\mathcal {O}}(\mathfrak l_\zeta )$
Recall that
![]() ${\mathcal {O}}(\mathfrak l_\zeta )$
denotes the BGG category of
${\mathcal {O}}(\mathfrak l_\zeta )$
denotes the BGG category of
![]() $\mathfrak l_\zeta $
-modules with respect to the Borel subalgebra
$\mathfrak l_\zeta $
-modules with respect to the Borel subalgebra
![]() $\mathfrak l_\zeta \cap \mathfrak b$
. Also,
$\mathfrak l_\zeta \cap \mathfrak b$
. Also,
![]() ${\mathcal {O}}(\mathfrak l_\zeta )_{\mathbb Z}$
denotes the integral BGG subcategory of
${\mathcal {O}}(\mathfrak l_\zeta )_{\mathbb Z}$
denotes the integral BGG subcategory of
![]() $\mathfrak l_\zeta $
-modules. In this subsection, we provide a characterization of objects in
$\mathfrak l_\zeta $
-modules. In this subsection, we provide a characterization of objects in
![]() ${\mathcal {O}}^{\zeta \text {-pres}}$
in terms of projective-injective modules in
${\mathcal {O}}^{\zeta \text {-pres}}$
in terms of projective-injective modules in
![]() ${\mathcal {O}}(\mathfrak l_\zeta )_{\mathbb Z}$
. In [Reference Konig and MazorchukKMa, Theorem 2], König and Mazorchuk have shown that objects in
${\mathcal {O}}(\mathfrak l_\zeta )_{\mathbb Z}$
. In [Reference Konig and MazorchukKMa, Theorem 2], König and Mazorchuk have shown that objects in
![]() ${\mathcal {O}}^{\zeta \text {-pres}}_{\bar 0}$
are modules in
${\mathcal {O}}^{\zeta \text {-pres}}_{\bar 0}$
are modules in
![]() ${\mathcal {O}}_{\bar 0}$
which, as
${\mathcal {O}}_{\bar 0}$
which, as
![]() $\mathfrak l_\zeta $
-modules, are presented by projective-injective modules in
$\mathfrak l_\zeta $
-modules, are presented by projective-injective modules in
![]() ${\mathcal {O}}(\mathfrak l_\zeta )_{\mathbb Z}$
. The following is a generalization to Lie superalgebras.
${\mathcal {O}}(\mathfrak l_\zeta )_{\mathbb Z}$
. The following is a generalization to Lie superalgebras.
Proposition 7. Let
![]() $M\in {\mathcal {O}}_{\mathbb Z}$
. Then the following are equivalent:
$M\in {\mathcal {O}}_{\mathbb Z}$
. Then the following are equivalent:
-
(1)
 $M\in {\mathcal {O}}^{{\zeta }\text {-pres}}$
.
$M\in {\mathcal {O}}^{{\zeta }\text {-pres}}$
. -
(2)
 $\operatorname {Res}\nolimits M\in {\mathcal {O}}_{\bar 0}^{{\zeta }\text {-pres}}$
.
$\operatorname {Res}\nolimits M\in {\mathcal {O}}_{\bar 0}^{{\zeta }\text {-pres}}$
. -
(3)
 $\operatorname {Res}\nolimits _{\mathfrak l_\zeta }^{\mathfrak {g}} M$
is a direct sum of modules having a two-step presentation by projective-injective modules in
$\operatorname {Res}\nolimits _{\mathfrak l_\zeta }^{\mathfrak {g}} M$
is a direct sum of modules having a two-step presentation by projective-injective modules in
 ${\mathcal {O}}(\mathfrak l_\zeta )$
.
${\mathcal {O}}(\mathfrak l_\zeta )$
.
Before we prove Proposition 7, we need some preparatory results. Recall that a projective module
![]() $M\in {\mathcal {O}}$
is said to be admissible if M is a direct sum of projective modules of the form
$M\in {\mathcal {O}}$
is said to be admissible if M is a direct sum of projective modules of the form
![]() $P(\lambda )$
with
$P(\lambda )$
with
![]() $\lambda \in {\Lambda (\zeta )}$
. For any
$\lambda \in {\Lambda (\zeta )}$
. For any
![]() $M\in {\mathcal {O}}$
, we let
$M\in {\mathcal {O}}$
, we let
![]() $Tr(M)$
and
$Tr(M)$
and
![]() $Tr_0(\operatorname {Res}\nolimits M)$
denote the sum of images of homomorphisms from admissible projective modules in
$Tr_0(\operatorname {Res}\nolimits M)$
denote the sum of images of homomorphisms from admissible projective modules in
![]() ${\mathcal {O}}$
(respectively, in
${\mathcal {O}}$
(respectively, in
![]() ${\mathcal {O}}_{\bar 0}$
) to M (respectively, to
${\mathcal {O}}_{\bar 0}$
) to M (respectively, to
![]() $\operatorname {Res}\nolimits M$
). Recall the coapproximation functor
$\operatorname {Res}\nolimits M$
). Recall the coapproximation functor
![]() $\mathfrak j_0:{\mathcal {O}}_{\bar 0}\rightarrow {\mathcal {O}}^{\zeta \text {-pres}}_{\bar 0}$
with respect to admissible projective modules studied in [Reference Mazorchuk and StroppelMSt, Section 2.4]; see also [Reference AuslanderAu, Section 3]. In general, we define the coapproximation functor
$\mathfrak j_0:{\mathcal {O}}_{\bar 0}\rightarrow {\mathcal {O}}^{\zeta \text {-pres}}_{\bar 0}$
with respect to admissible projective modules studied in [Reference Mazorchuk and StroppelMSt, Section 2.4]; see also [Reference AuslanderAu, Section 3]. In general, we define the coapproximation functor
![]() $\mathfrak j:{\mathcal {O}}\rightarrow {\mathcal {O}}^{\zeta \text {-pres}}$
for Lie superalgebras in the same fashion. Let
$\mathfrak j:{\mathcal {O}}\rightarrow {\mathcal {O}}^{\zeta \text {-pres}}$
for Lie superalgebras in the same fashion. Let
![]() $M\in {\mathcal {O}}$
with an epimorphism
$M\in {\mathcal {O}}$
with an epimorphism
![]() $f:P_M\twoheadrightarrow Tr(M)$
from a projective module
$f:P_M\twoheadrightarrow Tr(M)$
from a projective module
![]() $P_M\in {\mathcal {O}}$
. Then,
$P_M\in {\mathcal {O}}$
. Then,
![]() $\mathfrak j(M)$
is defined to be the quotient module
$\mathfrak j(M)$
is defined to be the quotient module
![]() $P_M/Tr(\text {ker}(f)).$
This definition is independent of the choices made. We refer to [Reference AuslanderAu, Section 3] and [Reference Khomenko and MazorchukKM, Section 2.4] for more details.
$P_M/Tr(\text {ker}(f)).$
This definition is independent of the choices made. We refer to [Reference AuslanderAu, Section 3] and [Reference Khomenko and MazorchukKM, Section 2.4] for more details.
We need the following auxiliary lemma.
Lemma 8. We have
![]() $\operatorname {Res}\nolimits \mathfrak j(M)\cong \mathfrak j_0\operatorname {Res}\nolimits (M)$
, for any
$\operatorname {Res}\nolimits \mathfrak j(M)\cong \mathfrak j_0\operatorname {Res}\nolimits (M)$
, for any
![]() $M\in {\mathcal {O}}$
.
$M\in {\mathcal {O}}$
.
Proof. It suffices to show that
![]() $\operatorname {Res}\nolimits Tr(M)=Tr_0(\operatorname {Res}\nolimits M)$
for any
$\operatorname {Res}\nolimits Tr(M)=Tr_0(\operatorname {Res}\nolimits M)$
for any
![]() $M\in {\mathcal {O}}$
. To see this, let
$M\in {\mathcal {O}}$
. To see this, let
![]() $\phi : Q\rightarrow \operatorname {Res}\nolimits M$
be a homomorphism from an admissible projective module
$\phi : Q\rightarrow \operatorname {Res}\nolimits M$
be a homomorphism from an admissible projective module
![]() $Q\in {\mathcal {O}}_{\bar 0}$
to
$Q\in {\mathcal {O}}_{\bar 0}$
to
![]() $\operatorname {Res}\nolimits M$
. This gives rise to
$\operatorname {Res}\nolimits M$
. This gives rise to
![]() $\operatorname {Ind}\nolimits \phi :\operatorname {Ind}\nolimits Q\rightarrow M$
with
$\operatorname {Ind}\nolimits \phi :\operatorname {Ind}\nolimits Q\rightarrow M$
with
![]() $\operatorname {Ind}\nolimits Q$
admissible in
$\operatorname {Ind}\nolimits Q$
admissible in
![]() ${\mathcal {O}}$
by Lemma 3. Now, the image of
${\mathcal {O}}$
by Lemma 3. Now, the image of
![]() $\phi $
is contained in the image of
$\phi $
is contained in the image of
![]() $\operatorname {Res}\nolimits \operatorname {Ind}\nolimits (\phi ): \operatorname {Res}\nolimits \operatorname {Ind}\nolimits Q\rightarrow \operatorname {Res}\nolimits M$
since
$\operatorname {Res}\nolimits \operatorname {Ind}\nolimits (\phi ): \operatorname {Res}\nolimits \operatorname {Ind}\nolimits Q\rightarrow \operatorname {Res}\nolimits M$
since
![]() $ Q$
is a direct summand of the admissible projective module
$ Q$
is a direct summand of the admissible projective module
![]() $\operatorname {Res}\nolimits \operatorname {Ind}\nolimits Q$
, which shows that
$\operatorname {Res}\nolimits \operatorname {Ind}\nolimits Q$
, which shows that
![]() $Tr(M)\supseteq Tr_0(\operatorname {Res}\nolimits M).$
Conversely, let
$Tr(M)\supseteq Tr_0(\operatorname {Res}\nolimits M).$
Conversely, let
![]() $\psi : P\rightarrow M$
be a homomorphism from an admissible projective module
$\psi : P\rightarrow M$
be a homomorphism from an admissible projective module
![]() $P\in {\mathcal {O}}$
. Since the image of
$P\in {\mathcal {O}}$
. Since the image of
![]() $\psi $
is equal to that of
$\psi $
is equal to that of
![]() $\operatorname {Res}\nolimits (\psi )$
and
$\operatorname {Res}\nolimits (\psi )$
and
![]() $\operatorname {Res}\nolimits P$
is admissible in
$\operatorname {Res}\nolimits P$
is admissible in
![]() ${\mathcal {O}}_{\bar 0}$
by Lemma 3 again, it follows that they are contained in
${\mathcal {O}}_{\bar 0}$
by Lemma 3 again, it follows that they are contained in
![]() $Tr_0(\operatorname {Res}\nolimits M)$
. This completes the proof.
$Tr_0(\operatorname {Res}\nolimits M)$
. This completes the proof.
Proof of Proposition 7.
The equivalence between
![]() $(2)$
and
$(2)$
and
![]() $(3)$
is a consequence of [Reference Konig and MazorchukKMa, Theorem 2]. Also,
$(3)$
is a consequence of [Reference Konig and MazorchukKMa, Theorem 2]. Also,
![]() $(1)\Rightarrow (2)$
is a direct consequence of Lemma 3. So it remains to show that
$(1)\Rightarrow (2)$
is a direct consequence of Lemma 3. So it remains to show that
![]() $(2)\Rightarrow (1)$
. Since
$(2)\Rightarrow (1)$
. Since
![]() $\operatorname {Res}\nolimits M\in {\mathcal {O}}^{\zeta \text {-pres}}_{\bar 0}$
, it follows that every simple quotient of M is
$\operatorname {Res}\nolimits M\in {\mathcal {O}}^{\zeta \text {-pres}}_{\bar 0}$
, it follows that every simple quotient of M is
![]() $ \alpha $
-free for any
$ \alpha $
-free for any
![]() $\alpha \in \Pi _\zeta $
. This implies that the top of M is a direct sum of modules of the form
$\alpha \in \Pi _\zeta $
. This implies that the top of M is a direct sum of modules of the form
![]() $L(\lambda )$
with
$L(\lambda )$
with
![]() $\lambda \in {\Lambda (\zeta )}$
. Therefore, there is an epimorphism
$\lambda \in {\Lambda (\zeta )}$
. Therefore, there is an epimorphism
![]() $f: P\twoheadrightarrow M$
for some admissible projective module
$f: P\twoheadrightarrow M$
for some admissible projective module
![]() $P\in {\mathcal {O}}$
. Consequently, we obtain an epimorphism from
$P\in {\mathcal {O}}$
. Consequently, we obtain an epimorphism from
![]() $\mathfrak j(M)$
to M.
$\mathfrak j(M)$
to M.
However, we note that
![]() $\operatorname {Res}\nolimits M\in {\mathcal {O}}^{\zeta \text {-pres}}_{\bar 0}$
if and only if
$\operatorname {Res}\nolimits M\in {\mathcal {O}}^{\zeta \text {-pres}}_{\bar 0}$
if and only if
![]() $\mathfrak j_0(\operatorname {Res}\nolimits M)\cong \operatorname {Res}\nolimits M$
. It follows that
$\mathfrak j_0(\operatorname {Res}\nolimits M)\cong \operatorname {Res}\nolimits M$
. It follows that
![]() $\operatorname {Res}\nolimits \mathfrak j(M)\cong \operatorname {Res}\nolimits M$
by Lemma 8. Consequently, the epimorphism from
$\operatorname {Res}\nolimits \mathfrak j(M)\cong \operatorname {Res}\nolimits M$
by Lemma 8. Consequently, the epimorphism from
![]() $\mathfrak j(M)$
to M is an isomorphism, as desired.
$\mathfrak j(M)$
to M is an isomorphism, as desired.
Remark 9. We remark that there is an analogue of Lemma 8 for the full subcategory of injectively copresentable modules of
![]() ${\mathcal {O}}$
in [Reference ChenCh2, Theorem 10], which is proved by means of Deodhar-Mathieu’s version of Enright completion functors. In fact, these functors are isomorphic to certain approximation functors, which are the dual version of the coapproximation functors introduced above; see also [Reference Konig and MazorchukKMa, Section 2, Theorem 2], [Reference Khomenko and MazorchukKM, Theorem 5].
${\mathcal {O}}$
in [Reference ChenCh2, Theorem 10], which is proved by means of Deodhar-Mathieu’s version of Enright completion functors. In fact, these functors are isomorphic to certain approximation functors, which are the dual version of the coapproximation functors introduced above; see also [Reference Konig and MazorchukKMa, Section 2, Theorem 2], [Reference Khomenko and MazorchukKM, Theorem 5].
4.2. Standard and proper standard objects.
Recall that
![]() $P(\lambda )$
and
$P(\lambda )$
and
![]() $P_0(\lambda )$
denote the projective covers of
$P_0(\lambda )$
denote the projective covers of
![]() $L(\lambda )$
and
$L(\lambda )$
and
![]() $L_0(\lambda )$
in
$L_0(\lambda )$
in
![]() ${\mathcal {O}}$
and
${\mathcal {O}}$
and
![]() ${\mathcal {O}}_{\bar 0}$
, respectively. For
${\mathcal {O}}_{\bar 0}$
, respectively. For
![]() $\lambda \in \Lambda (\zeta )$
, we define the proper standard object
$\lambda \in \Lambda (\zeta )$
, we define the proper standard object
![]() $\overline \Delta (\lambda )$
for
$\overline \Delta (\lambda )$
for
![]() ${\mathcal {O}}^{{\zeta }\text {-pres}}$
to be
${\mathcal {O}}^{{\zeta }\text {-pres}}$
to be
![]() $P(\lambda )/ Tr(K_\lambda )$
, where
$P(\lambda )/ Tr(K_\lambda )$
, where
![]() $K_\lambda $
is the kernel of the canonical quotient
$K_\lambda $
is the kernel of the canonical quotient
![]() $P(\lambda )\rightarrow M(\lambda )$
. Note that the proper standard objects indeed lie in
$P(\lambda )\rightarrow M(\lambda )$
. Note that the proper standard objects indeed lie in
![]() ${\mathcal {O}}^{{\zeta }\text {-pres}}$
and furthermore,
${\mathcal {O}}^{{\zeta }\text {-pres}}$
and furthermore,
We also define the standard object
![]() $\Delta (\lambda )$
for
$\Delta (\lambda )$
for
![]() ${\mathcal {O}}^{{\zeta }\text {-pres}}$
by
${\mathcal {O}}^{{\zeta }\text {-pres}}$
by
Here,
![]() $P_{\mathfrak {l}_\zeta }(\lambda )$
is regarded as a
$P_{\mathfrak {l}_\zeta }(\lambda )$
is regarded as a
![]() $\mathfrak {p}$
-module by letting
$\mathfrak {p}$
-module by letting
![]() $\frak u^+$
act trivially. Similarly, we define
$\frak u^+$
act trivially. Similarly, we define
![]() $\Delta _0(\lambda ):= \operatorname {Ind}\nolimits _{\mathfrak p_{\bar 0}}^{\mathfrak {g}_{\bar 0}} P_{\mathfrak l_\zeta }(\lambda ). $
It follows from Proposition 7 that
$\Delta _0(\lambda ):= \operatorname {Ind}\nolimits _{\mathfrak p_{\bar 0}}^{\mathfrak {g}_{\bar 0}} P_{\mathfrak l_\zeta }(\lambda ). $
It follows from Proposition 7 that
![]() $\Delta (\lambda )$
is an object in
$\Delta (\lambda )$
is an object in
![]() ${\mathcal {O}}^{\zeta \text {-pres}}$
. We will provide an alternative proof in Corollary 15 below.
${\mathcal {O}}^{\zeta \text {-pres}}$
. We will provide an alternative proof in Corollary 15 below.
We set
![]() $\mathcal F(\Delta )$
to be the full subcategory of
$\mathcal F(\Delta )$
to be the full subcategory of
![]() ${\mathcal {O}}$
consisting of modules which admit a
${\mathcal {O}}$
consisting of modules which admit a
![]() $\Delta $
-flag. Similarly, we define
$\Delta $
-flag. Similarly, we define
![]() $\mathcal F(\Delta _0)\subset {\mathcal {O}}_{\bar 0}$
.
$\mathcal F(\Delta _0)\subset {\mathcal {O}}_{\bar 0}$
.
Lemma 10. For any
![]() $V\in \mathcal F(\Delta _0)$
, we have
$V\in \mathcal F(\Delta _0)$
, we have
![]() $\operatorname {Ind}\nolimits (V)\in \mathcal F(\Delta )$
.
$\operatorname {Ind}\nolimits (V)\in \mathcal F(\Delta )$
.
Proof. It is sufficient to prove this for
![]() $V=\Delta _0(\lambda )$
with
$V=\Delta _0(\lambda )$
with
![]() $\lambda \in {\Lambda (\zeta )}$
. We note that
$\lambda \in {\Lambda (\zeta )}$
. We note that
We claim that the
![]() $\mathfrak p$
-module
$\mathfrak p$
-module
![]() $\operatorname {Ind}\nolimits ^{\mathfrak p}_{\mathfrak p_{\bar 0}}P_{\mathfrak l_\zeta }(\lambda )$
has a filtration any subquotient S of which is of the form
$\operatorname {Ind}\nolimits ^{\mathfrak p}_{\mathfrak p_{\bar 0}}P_{\mathfrak l_\zeta }(\lambda )$
has a filtration any subquotient S of which is of the form
![]() $\operatorname {Res}\nolimits _{\mathfrak l_\zeta }^{\mathfrak p}S\cong P_{\mathfrak l_\zeta }(\gamma )$
with
$\operatorname {Res}\nolimits _{\mathfrak l_\zeta }^{\mathfrak p}S\cong P_{\mathfrak l_\zeta }(\gamma )$
with
![]() $\gamma \in {\Lambda (\zeta )}$
and
$\gamma \in {\Lambda (\zeta )}$
and
![]() $\mathfrak u^+S=0$
. To see this, we recall the grading operator
$\mathfrak u^+S=0$
. To see this, we recall the grading operator
![]() $H\in \mathfrak h$
introduced in (1.4).
$H\in \mathfrak h$
introduced in (1.4).
Set
![]() $E:=U(\mathfrak u^+_{\bar 1})$
, which is an
$E:=U(\mathfrak u^+_{\bar 1})$
, which is an
![]() $\mathfrak l_\zeta $
-submodule of
$\mathfrak l_\zeta $
-submodule of
![]() $U(\mathfrak g)$
under the adjoint action. For each complex number
$U(\mathfrak g)$
under the adjoint action. For each complex number
![]() $c\in {\mathbb {C}}$
, we let
$c\in {\mathbb {C}}$
, we let
![]() $E_c$
denote the c-eigenspace of H under the adjoint action. Since H lies in the center of
$E_c$
denote the c-eigenspace of H under the adjoint action. Since H lies in the center of
![]() $\mathfrak l_\zeta $
, it follows that each
$\mathfrak l_\zeta $
, it follows that each
![]() $E_c$
is an
$E_c$
is an
![]() $\mathfrak l_\zeta $
-submodule of E. Then, E decomposes into a sum of
$\mathfrak l_\zeta $
-submodule of E. Then, E decomposes into a sum of
![]() $\mathfrak l_\zeta $
-submodules
$\mathfrak l_\zeta $
-submodules
for some
![]() $c_1,\ldots ,c_k\in {\mathbb {C}}$
such that
$c_1,\ldots ,c_k\in {\mathbb {C}}$
such that
![]() $\text {Re}(c_1)<\text {Re}(c_2)<\cdots <\text {Re}(c_k)$
.
$\text {Re}(c_1)<\text {Re}(c_2)<\cdots <\text {Re}(c_k)$
.
We may note that
 $$ \begin{align} &\operatorname{Res}\nolimits_{\mathfrak l_\zeta}^{\mathfrak p}\operatorname{Ind}\nolimits_{\mathfrak p_{\bar 0}}^{\mathfrak p}P_{\mathfrak l_\zeta}(\lambda)\cong E\otimes P_{\mathfrak l_\zeta}(\lambda) = \bigoplus_{i=1}^k (E_{c_i} \otimes P_{\mathfrak l_\zeta}(\lambda)) \end{align} $$
$$ \begin{align} &\operatorname{Res}\nolimits_{\mathfrak l_\zeta}^{\mathfrak p}\operatorname{Ind}\nolimits_{\mathfrak p_{\bar 0}}^{\mathfrak p}P_{\mathfrak l_\zeta}(\lambda)\cong E\otimes P_{\mathfrak l_\zeta}(\lambda) = \bigoplus_{i=1}^k (E_{c_i} \otimes P_{\mathfrak l_\zeta}(\lambda)) \end{align} $$
is a direct sum of projective-injective
![]() $\mathfrak l_\zeta $
-modules in the category
$\mathfrak l_\zeta $
-modules in the category
![]() ${\mathcal {O}}(\mathfrak l_\zeta )$
, each of which is of the form
${\mathcal {O}}(\mathfrak l_\zeta )$
, each of which is of the form
![]() $P_{\mathfrak l_\zeta }(\gamma )$
with
$P_{\mathfrak l_\zeta }(\gamma )$
with
![]() $\gamma \in {\Lambda (\zeta )}$
. Furthermore, we define a filtration
$\gamma \in {\Lambda (\zeta )}$
. Furthermore, we define a filtration
by letting
 $$ \begin{align} &\operatorname{Ind}\nolimits_{\mathfrak p_{\bar 0}}^{\mathfrak p}P_{\mathfrak l_\zeta}(\lambda)_j:= \bigoplus_{i=j}^k (E_{c_i} \otimes P_{\mathfrak l_\zeta}(\lambda)), \end{align} $$
$$ \begin{align} &\operatorname{Ind}\nolimits_{\mathfrak p_{\bar 0}}^{\mathfrak p}P_{\mathfrak l_\zeta}(\lambda)_j:= \bigoplus_{i=j}^k (E_{c_i} \otimes P_{\mathfrak l_\zeta}(\lambda)), \end{align} $$
for
![]() $j=1,\ldots , k$
. Fix
$j=1,\ldots , k$
. Fix
![]() $1\leq j\leq k$
. We note that both
$1\leq j\leq k$
. We note that both
![]() $\mathfrak u_{\bar 1}^+E_{c_j}$
and
$\mathfrak u_{\bar 1}^+E_{c_j}$
and
![]() $[\mathfrak u_{\bar 0}^+, E_{c_j}]$
are subspaces of
$[\mathfrak u_{\bar 0}^+, E_{c_j}]$
are subspaces of
![]() $ \bigoplus _{i>j}E_{c_i}.$
Consequently, we have
$ \bigoplus _{i>j}E_{c_i}.$
Consequently, we have
Therefore, the filtration (4.6) gives rise to the desired filtration. This completes the proof.
Lemma 11. Suppose that
![]() $M\in {\mathcal {O}}$
and
$M\in {\mathcal {O}}$
and
![]() $c\in {\mathbb {C}}$
. Let
$c\in {\mathbb {C}}$
. Let
![]() $M_c$
be the c-eigenspace with respect to the action of the grading operator H from (1.4). Then we have
$M_c$
be the c-eigenspace with respect to the action of the grading operator H from (1.4). Then we have
-
(1) There is
 $d\in {\mathbb {C}}$
such that
$d\in {\mathbb {C}}$
such that
 $M_{d} \neq 0$
and
$M_{d} \neq 0$
and
 $M_c=0$
for
$M_c=0$
for
 $\text {Re}(c)>\text {Re}(d).$
$\text {Re}(c)>\text {Re}(d).$
-
(2)
 $M_c$
is an object in
$M_c$
is an object in
 ${\mathcal {O}}(\mathfrak l_\zeta )$
.
${\mathcal {O}}(\mathfrak l_\zeta )$
. -
(3) If M is a (possibly infinite) direct sum of projective-injective modules in
 ${\mathcal {O}}(\mathfrak l_\zeta )$
, then so is
${\mathcal {O}}(\mathfrak l_\zeta )$
, then so is
 $M_c$
.
$M_c$
.
Proof. Since H acts on any
![]() $\mathfrak h$
-weight subspace of M as a scalar and M is finitely generated as an
$\mathfrak h$
-weight subspace of M as a scalar and M is finitely generated as an
![]() $\mathfrak n^-$
-module, the conclusion in Part (1) follows.
$\mathfrak n^-$
-module, the conclusion in Part (1) follows.
For the proof of Part (2), we note that
![]() $M_c$
is an
$M_c$
is an
![]() $\mathfrak l_\zeta $
-module, locally finite over
$\mathfrak l_\zeta $
-module, locally finite over
![]() $ \mathfrak l_\zeta \cap \mathfrak b$
and semisimple over
$ \mathfrak l_\zeta \cap \mathfrak b$
and semisimple over
![]() $\mathfrak h$
. Now, if M is simple, then M is an epimorphic image of
$\mathfrak h$
. Now, if M is simple, then M is an epimorphic image of
![]() $\operatorname {Ind}\nolimits _{\mathfrak p_{\bar 0}}^{\mathfrak g}L_{\mathfrak l_\zeta }(\lambda )$
, for some
$\operatorname {Ind}\nolimits _{\mathfrak p_{\bar 0}}^{\mathfrak g}L_{\mathfrak l_\zeta }(\lambda )$
, for some
![]() $\lambda \in \mathfrak {h}^\ast $
. Since
$\lambda \in \mathfrak {h}^\ast $
. Since
![]() $\operatorname {Ind}\nolimits _{\mathfrak p_{\bar 0}}^{\mathfrak g}L_{\mathfrak l_\zeta }(\lambda )_c$
is finitely generated, so is
$\operatorname {Ind}\nolimits _{\mathfrak p_{\bar 0}}^{\mathfrak g}L_{\mathfrak l_\zeta }(\lambda )_c$
is finitely generated, so is
![]() $M_c$
. Consequently,
$M_c$
. Consequently,
![]() $M_c \in {\mathcal {O}}(\mathfrak l_\zeta )$
by induction on the length of the module M in
$M_c \in {\mathcal {O}}(\mathfrak l_\zeta )$
by induction on the length of the module M in
![]() ${\mathcal {O}}$
.
${\mathcal {O}}$
.
Finally, suppose that
![]() $\operatorname {Res}\nolimits _{\mathfrak l_\zeta }^{\mathfrak {g}}M= \bigoplus _{\lambda \in \mathcal X}X_\lambda $
, where
$\operatorname {Res}\nolimits _{\mathfrak l_\zeta }^{\mathfrak {g}}M= \bigoplus _{\lambda \in \mathcal X}X_\lambda $
, where
![]() $X_\lambda \cong {P_{\mathfrak l_\zeta }}(\lambda )$
are projective-injective modules in
$X_\lambda \cong {P_{\mathfrak l_\zeta }}(\lambda )$
are projective-injective modules in
![]() ${\mathcal {O}}(\mathfrak l_\zeta )$
for some
${\mathcal {O}}(\mathfrak l_\zeta )$
for some
![]() $\lambda $
lying in some index set
$\lambda $
lying in some index set
![]() $\mathcal X$
. Since each
$\mathcal X$
. Since each
![]() $X_\lambda $
is indecomposable and H acts on
$X_\lambda $
is indecomposable and H acts on
![]() $X_\lambda $
semisimply, it follows that
$X_\lambda $
semisimply, it follows that
![]() $(H-\chi _{\lambda }^{\mathfrak l_\zeta }(H))X_\lambda =0.$
Therefore,
$(H-\chi _{\lambda }^{\mathfrak l_\zeta }(H))X_\lambda =0.$
Therefore,
![]() $M_c$
is projective-injective in
$M_c$
is projective-injective in
![]() ${\mathcal {O}}(\mathfrak l_\zeta )$
. This completes the proof.
${\mathcal {O}}(\mathfrak l_\zeta )$
. This completes the proof.
Lemma 12. Let
![]() $M\in \mathcal F(\Delta )$
. Then we have
$M\in \mathcal F(\Delta )$
. Then we have
-
(1)
 $\operatorname {Res}\nolimits _{\mathfrak l_\zeta }^{\mathfrak {g}}M$
is a direct sum of projective-injective
$\operatorname {Res}\nolimits _{\mathfrak l_\zeta }^{\mathfrak {g}}M$
is a direct sum of projective-injective
 $\mathfrak l_\zeta $
-modules in
$\mathfrak l_\zeta $
-modules in
 ${\mathcal {O}}(\mathfrak l_\zeta ).$
${\mathcal {O}}(\mathfrak l_\zeta ).$
-
(2)
 $\operatorname {Res}\nolimits M\in \mathcal F(\Delta _0)$
.
$\operatorname {Res}\nolimits M\in \mathcal F(\Delta _0)$
.
Proof. It suffices to prove the assertions for
![]() $M= \Delta (\lambda )$
, for a given
$M= \Delta (\lambda )$
, for a given
![]() $\lambda \in {\Lambda (\zeta )}$
.
$\lambda \in {\Lambda (\zeta )}$
.
We have
![]() $\operatorname {Res}\nolimits _{\mathfrak l_\zeta }^{\mathfrak {g}}\Delta (\lambda )\cong U(\mathfrak u^-)\otimes {P_{\mathfrak l_\zeta }}(\lambda )$
, and hence,
$\operatorname {Res}\nolimits _{\mathfrak l_\zeta }^{\mathfrak {g}}\Delta (\lambda )\cong U(\mathfrak u^-)\otimes {P_{\mathfrak l_\zeta }}(\lambda )$
, and hence,
![]() $\operatorname {Res}\nolimits _{\mathfrak l_\zeta }^{\mathfrak {g}}\Delta (\lambda )$
is a direct sum of projective-injective
$\operatorname {Res}\nolimits _{\mathfrak l_\zeta }^{\mathfrak {g}}\Delta (\lambda )$
is a direct sum of projective-injective
![]() $\mathfrak l_\zeta $
-modules in
$\mathfrak l_\zeta $
-modules in
![]() ${\mathcal {O}}(\mathfrak l_\zeta )$
. This proves Part (1).
${\mathcal {O}}(\mathfrak l_\zeta )$
. This proves Part (1).
Since
![]() $\Delta (\lambda )$
has a
$\Delta (\lambda )$
has a
![]() $\mathfrak {g}_{\bar 0}$
-Verma flag as well, Part (2) now follows from [Reference Mazorchuk and StroppelMSt, Proposition 2.13(i),(ii)].
$\mathfrak {g}_{\bar 0}$
-Verma flag as well, Part (2) now follows from [Reference Mazorchuk and StroppelMSt, Proposition 2.13(i),(ii)].
The following is a generalization of [Reference Mazorchuk and StroppelMSt, Corollary 2.14], where the case of Lie algebras was considered. Here, we provide an alternative proof.
Proposition 13. The full subcategory
![]() $\mathcal F(\Delta )$
is closed under taking direct summands.
$\mathcal F(\Delta )$
is closed under taking direct summands.
Proof. Let
![]() $M\in \mathcal F(\Delta )$
. Set N to be a direct summand of M. We shall show that
$M\in \mathcal F(\Delta )$
. Set N to be a direct summand of M. We shall show that
![]() $N\in \mathcal F(\Delta )$
. Let
$N\in \mathcal F(\Delta )$
. Let
be a
![]() $\Delta $
-flag.
$\Delta $
-flag.
We decompose
![]() $\operatorname {Res}\nolimits ^{\mathfrak {g}}_{\mathfrak l_\zeta } M$
into a direct sum
$\operatorname {Res}\nolimits ^{\mathfrak {g}}_{\mathfrak l_\zeta } M$
into a direct sum
where
![]() $M_c$
is the c-eigenspace with respect to the action of the grading operator H from (1.4). By Lemmas 11 and 12, each
$M_c$
is the c-eigenspace with respect to the action of the grading operator H from (1.4). By Lemmas 11 and 12, each
![]() $M_c$
is a projective-injective module in
$M_c$
is a projective-injective module in
![]() ${\mathcal {O}}(\mathfrak l_\zeta )$
. Also, there is a complex number
${\mathcal {O}}(\mathfrak l_\zeta )$
. Also, there is a complex number
![]() $d\in {\mathbb {C}}$
such that
$d\in {\mathbb {C}}$
such that
![]() $M_d\neq 0$
and
$M_d\neq 0$
and
![]() $M_c=0$
for any
$M_c=0$
for any
![]() $c\in {\mathbb {C}}$
with
$c\in {\mathbb {C}}$
with
![]() $\text {Re}(c)>\text {Re}(d)$
.
$\text {Re}(c)>\text {Re}(d)$
.
Note that
![]() $U(\mathfrak {g})V=U(\mathfrak u^-)V$
, for any direct summand V of
$U(\mathfrak {g})V=U(\mathfrak u^-)V$
, for any direct summand V of
![]() $M_d$
. We claim that both
$M_d$
. We claim that both
![]() $U(\mathfrak {g})V$
and
$U(\mathfrak {g})V$
and
![]() $M/(U(\mathfrak {g})V)$
lie in
$M/(U(\mathfrak {g})V)$
lie in
![]() $\mathcal F(\Delta )$
. We shall prove by induction on the length k. The conclusion for the case
$\mathcal F(\Delta )$
. We shall prove by induction on the length k. The conclusion for the case
![]() $k=1$
holds since
$k=1$
holds since
![]() $U(\mathfrak {g})M_d=M$
in this case.
$U(\mathfrak {g})M_d=M$
in this case.
Since (4.9) is a
![]() $\Delta $
-flag, there is
$\Delta $
-flag, there is
![]() $1\leq i< k+1$
with the canonical quotient
$1\leq i< k+1$
with the canonical quotient
![]() $p: M^{i}\twoheadrightarrow M^{i}/M^{i+1}$
such that
$p: M^{i}\twoheadrightarrow M^{i}/M^{i+1}$
such that
for some
![]() $\lambda \in {\Lambda (\zeta )}.$
Consider the following split short exact sequence induced by p and the inclusion
$\lambda \in {\Lambda (\zeta )}.$
Consider the following split short exact sequence induced by p and the inclusion
![]() $M^{i+1}\hookrightarrow M^i$
$M^{i+1}\hookrightarrow M^i$
in
![]() ${\mathcal {O}}(\mathfrak l_\zeta )$
. We get an
${\mathcal {O}}(\mathfrak l_\zeta )$
. We get an
![]() $\mathfrak l_\zeta $
-submodule S of
$\mathfrak l_\zeta $
-submodule S of
![]() $M_d$
such that
$M_d$
such that
![]() $p|_S: S\rightarrow {P_{\mathfrak l_\zeta }}(\lambda )$
is an isomorphism of
$p|_S: S\rightarrow {P_{\mathfrak l_\zeta }}(\lambda )$
is an isomorphism of
![]() $\mathfrak l_\zeta $
-modules. Since
$\mathfrak l_\zeta $
-modules. Since
![]() $U(\mathfrak {g})S=U(\mathfrak u^-)S$
, as observed above, it follows that p restricts to a
$U(\mathfrak {g})S=U(\mathfrak u^-)S$
, as observed above, it follows that p restricts to a
![]() $\mathfrak {g}$
-module isomorphism from
$\mathfrak {g}$
-module isomorphism from
![]() $U(\mathfrak g)S$
to
$U(\mathfrak g)S$
to
![]() $M^{i}/M^{i+1}\cong \operatorname {Ind}\nolimits _{\mathfrak p}^{\mathfrak {g}}{P_{\mathfrak l_\zeta }}(\lambda ).$
Consequently, we get a split short exact sequence
$M^{i}/M^{i+1}\cong \operatorname {Ind}\nolimits _{\mathfrak p}^{\mathfrak {g}}{P_{\mathfrak l_\zeta }}(\lambda ).$
Consequently, we get a split short exact sequence
in
![]() ${\mathcal {O}}$
.
${\mathcal {O}}$
.
Put
![]() $K:=U(\mathfrak {g})S$
, and so
$K:=U(\mathfrak {g})S$
, and so
![]() $M^{i}=K\oplus M^{i+1}$
. Consider the exact sequence
$M^{i}=K\oplus M^{i+1}$
. Consider the exact sequence
Since both
![]() $M^{i+1}$
and
$M^{i+1}$
and
![]() $M/M^i$
lie in
$M/M^i$
lie in
![]() $\mathcal F(\Delta )$
, it follows that
$\mathcal F(\Delta )$
, it follows that
![]() $M/K$
is an object in
$M/K$
is an object in
![]() $\mathcal F(\Delta )$
. By induction, it follows that
$\mathcal F(\Delta )$
. By induction, it follows that
![]() $U(\mathfrak g)M_d=U(\mathfrak u^-)M_d\cong \operatorname {Ind}\nolimits _{\mathfrak p}^{\mathfrak {g}} M_d$
is a direct sum of standard objects
$U(\mathfrak g)M_d=U(\mathfrak u^-)M_d\cong \operatorname {Ind}\nolimits _{\mathfrak p}^{\mathfrak {g}} M_d$
is a direct sum of standard objects
![]() $\Delta (\mu )$
, for
$\Delta (\mu )$
, for
![]() $\mu \in {\Lambda (\zeta )}$
, and
$\mu \in {\Lambda (\zeta )}$
, and
![]() $M/(U(\mathfrak {g})M_d)$
lies in
$M/(U(\mathfrak {g})M_d)$
lies in
![]() $\mathcal F(\Delta )$
. Let V be a direct summand of
$\mathcal F(\Delta )$
. Let V be a direct summand of
![]() $M_d$
. Then
$M_d$
. Then
![]() $U(\mathfrak {g})V\cong \operatorname {Ind}\nolimits _{\mathfrak p}^{\mathfrak {g}} V\in \mathcal F(\Delta )$
and
$U(\mathfrak {g})V\cong \operatorname {Ind}\nolimits _{\mathfrak p}^{\mathfrak {g}} V\in \mathcal F(\Delta )$
and
![]() $U(\mathfrak g)(M/V)\cong \operatorname {Ind}\nolimits _{\mathfrak p}^{\mathfrak {g}} (M/V)\in \mathcal F(\Delta )$
. Consequently, we have
$U(\mathfrak g)(M/V)\cong \operatorname {Ind}\nolimits _{\mathfrak p}^{\mathfrak {g}} (M/V)\in \mathcal F(\Delta )$
. Consequently, we have
![]() $M/(U(\mathfrak {g})V)\in \mathcal F(\Delta )$
, as desired.
$M/(U(\mathfrak {g})V)\in \mathcal F(\Delta )$
, as desired.
Finally, let
![]() $M=N\oplus N'$
. Then, either
$M=N\oplus N'$
. Then, either
![]() $N_d\neq 0$
or
$N_d\neq 0$
or
![]() $N^{\prime }_d\neq 0$
. Without loss of generality, we may assume that
$N^{\prime }_d\neq 0$
. Without loss of generality, we may assume that
![]() $N_d\neq 0$
, and then
$N_d\neq 0$
, and then
![]() $M/(U(\mathfrak {g})N_d) = (N/U(\mathfrak {g})N_d)\oplus N'$
has a
$M/(U(\mathfrak {g})N_d) = (N/U(\mathfrak {g})N_d)\oplus N'$
has a
![]() $\Delta $
-flag by the argument above. By induction on the length of M, it follows that
$\Delta $
-flag by the argument above. By induction on the length of M, it follows that
![]() $N/(U(\mathfrak {g})N_d)$
and
$N/(U(\mathfrak {g})N_d)$
and
![]() $N'$
have
$N'$
have
![]() $\Delta $
-flags, and hence N as well. This completes the proof.
$\Delta $
-flags, and hence N as well. This completes the proof.
4.3. Stratified structure and BGG reciprocity
We denote by
![]() $\leq $
the partial order on
$\leq $
the partial order on
![]() $\mathfrak h^\ast $
induced by the triangular decomposition (1.1). Namely, it is the transitive closure of the relations
$\mathfrak h^\ast $
induced by the triangular decomposition (1.1). Namely, it is the transitive closure of the relations
 $$ \begin{align*}\begin{cases} \lambda-\alpha \le\lambda, &\text{for a positive root}\ \alpha,\\ \lambda+\alpha \le\lambda, &\text{for a negative root}\ \alpha. \end{cases}\end{align*} $$
$$ \begin{align*}\begin{cases} \lambda-\alpha \le\lambda, &\text{for a positive root}\ \alpha,\\ \lambda+\alpha \le\lambda, &\text{for a negative root}\ \alpha. \end{cases}\end{align*} $$
Recall the Serre quotient category
![]() ${\overline {{\mathcal {O}}}}$
and the canonical quotient functor
${\overline {{\mathcal {O}}}}$
and the canonical quotient functor
![]() $\pi :{\mathcal {O}}_{\mathbb Z}\rightarrow {\overline {{\mathcal {O}}}}$
associated to
$\pi :{\mathcal {O}}_{\mathbb Z}\rightarrow {\overline {{\mathcal {O}}}}$
associated to
![]() $\zeta $
from Section 2.5. Lemma 10, combined with Proposition 13, has the following consequence. Namely, the category
$\zeta $
from Section 2.5. Lemma 10, combined with Proposition 13, has the following consequence. Namely, the category
![]() ${\mathcal {O}}^{{\zeta }\text {-pres}}$
is stratified.
${\mathcal {O}}^{{\zeta }\text {-pres}}$
is stratified.
Theorem 14. For any
![]() $\lambda \in {\Lambda (\zeta )}$
, we have the following.
$\lambda \in {\Lambda (\zeta )}$
, we have the following.
-
(1) There is a short exact sequence in
 ${\mathcal {O}}$
of the form (4.14)such that
${\mathcal {O}}$
of the form (4.14)such that $$ \begin{align} &0\rightarrow K(\lambda)\rightarrow P(\lambda)\rightarrow \Delta(\lambda)\rightarrow 0, \end{align} $$
$$ \begin{align} &0\rightarrow K(\lambda)\rightarrow P(\lambda)\rightarrow \Delta(\lambda)\rightarrow 0, \end{align} $$
 $K(\lambda )$
has a
$K(\lambda )$
has a
 $\Delta $
-flag, subquotients of which are isomorphic to
$\Delta $
-flag, subquotients of which are isomorphic to
 $\Delta (\mu )$
with
$\Delta (\mu )$
with
 $\lambda <\mu $
.
$\lambda <\mu $
.
-
(2) The object
 $\pi \overline \Delta (\lambda )$
surjects onto
$\pi \overline \Delta (\lambda )$
surjects onto
 $\pi L(\lambda )$
, and its kernel has a composition series, subquotients of which are isomorphic to
$\pi L(\lambda )$
, and its kernel has a composition series, subquotients of which are isomorphic to
 $\pi L(\mu )$
with
$\pi L(\mu )$
with
 $\mu \in {\Lambda (\zeta )}$
and
$\mu \in {\Lambda (\zeta )}$
and
 $\mu <\lambda $
.
$\mu <\lambda $
. -
(3) The object
 $\pi (\Delta (\lambda ))$
has a filtration, subquotients of which are isomorphic to
$\pi (\Delta (\lambda ))$
has a filtration, subquotients of which are isomorphic to
 $\overline \Delta (\lambda )$
.
$\overline \Delta (\lambda )$
.
Proof. Since
![]() $\operatorname {Res}\nolimits P(\lambda )$
is admissible by Lemma 3, it follows that
$\operatorname {Res}\nolimits P(\lambda )$
is admissible by Lemma 3, it follows that
![]() $\operatorname {Res}\nolimits P(\lambda )\in \mathcal F(\Delta _0)$
by [Reference Konig and MazorchukKMa, Lemma 4] and [Reference Mazorchuk and StroppelMSt, Propositions 2.9 and 2.13]. Alternatively, this also follows from the fact that
$\operatorname {Res}\nolimits P(\lambda )\in \mathcal F(\Delta _0)$
by [Reference Konig and MazorchukKMa, Lemma 4] and [Reference Mazorchuk and StroppelMSt, Propositions 2.9 and 2.13]. Alternatively, this also follows from the fact that
![]() $\operatorname {Res}\nolimits P(\lambda )$
is a direct summand of a sum of translations of a module of the form
$\operatorname {Res}\nolimits P(\lambda )$
is a direct summand of a sum of translations of a module of the form
![]() $\operatorname {Ind}\nolimits _{\mathfrak p_{\bar 0}}^{\mathfrak g_{\bar 0}}P_{\mathfrak l_\zeta }(\gamma )$
with
$\operatorname {Ind}\nolimits _{\mathfrak p_{\bar 0}}^{\mathfrak g_{\bar 0}}P_{\mathfrak l_\zeta }(\gamma )$
with
![]() $\gamma \in {\Lambda (\zeta )}$
; see also the proof of [Reference Konig and MazorchukKMa, Lemma 4]. By Lemma 10, we have
$\gamma \in {\Lambda (\zeta )}$
; see also the proof of [Reference Konig and MazorchukKMa, Lemma 4]. By Lemma 10, we have
![]() $\operatorname {Ind}\nolimits \operatorname {Res}\nolimits P(\lambda )\in \mathcal F(\Delta )$
. Since
$\operatorname {Ind}\nolimits \operatorname {Res}\nolimits P(\lambda )\in \mathcal F(\Delta )$
. Since
![]() $P(\lambda )$
is a direct summand of
$P(\lambda )$
is a direct summand of
![]() $\operatorname {Ind}\nolimits \operatorname {Res}\nolimits P(\lambda )$
, Part (1) follows from Proposition 13 and the BGG reciprocity for
$\operatorname {Ind}\nolimits \operatorname {Res}\nolimits P(\lambda )$
, Part (1) follows from Proposition 13 and the BGG reciprocity for
![]() ${\mathcal {O}}$
.
${\mathcal {O}}$
.
The exactness of
![]() $\pi $
and (4.1) imply that
$\pi $
and (4.1) imply that
![]() $\pi {\overline \Delta }(\lambda ) =\pi (M(\lambda ))$
, and hence, Part (2) follows.
$\pi {\overline \Delta }(\lambda ) =\pi (M(\lambda ))$
, and hence, Part (2) follows.
Finally, we prove Part (3). We note that, for a given
![]() $\gamma \in \Lambda $
with
$\gamma \in \Lambda $
with
![]() $\gamma \notin {\Lambda (\zeta )}$
, we have
$\gamma \notin {\Lambda (\zeta )}$
, we have
![]() $\pi (\operatorname {Ind}\nolimits _{\mathfrak p}^{\mathfrak {g}}L_{\mathfrak l_\zeta }(\gamma ))=0$
. The conclusion of Part (3) follows. This completes the proof.
$\pi (\operatorname {Ind}\nolimits _{\mathfrak p}^{\mathfrak {g}}L_{\mathfrak l_\zeta }(\gamma ))=0$
. The conclusion of Part (3) follows. This completes the proof.
Set
![]() $Q(\lambda )$
to be the quotient of
$Q(\lambda )$
to be the quotient of
![]() $P(\lambda )$
modulo the sum of the images of all homomorphisms
$P(\lambda )$
modulo the sum of the images of all homomorphisms
![]() $P(\mu )\rightarrow P(\lambda )$
, where
$P(\mu )\rightarrow P(\lambda )$
, where
![]() $\mu \in {\Lambda (\zeta )}$
and
$\mu \in {\Lambda (\zeta )}$
and
![]() $\mu>\lambda $
. Observe that
$\mu>\lambda $
. Observe that
![]() $Q(\lambda )\in {\mathcal {O}}^{{\zeta }\text {-pres}}.$
$Q(\lambda )\in {\mathcal {O}}^{{\zeta }\text {-pres}}.$
Corollary 15. For any
![]() $\lambda \in {\Lambda (\zeta )}$
, we have
$\lambda \in {\Lambda (\zeta )}$
, we have
![]() $\Delta (\lambda )\cong Q(\lambda )$
.
$\Delta (\lambda )\cong Q(\lambda )$
.
Proof. Let
![]() $K(\lambda )\in \mathcal F(\Delta )$
be the module given in Theorem 14(1). Then
$K(\lambda )\in \mathcal F(\Delta )$
be the module given in Theorem 14(1). Then
![]() $K(\lambda )$
has a
$K(\lambda )$
has a
![]() $\Delta $
-flag, subquotients of which are
$\Delta $
-flag, subquotients of which are
![]() $\Delta (\mu )$
with
$\Delta (\mu )$
with
![]() $\mu \in {\Lambda (\zeta )}$
and
$\mu \in {\Lambda (\zeta )}$
and
![]() $\mu>\lambda $
. Therefore,
$\mu>\lambda $
. Therefore,
![]() $K(\lambda )$
is the image of a homomorphism from an admissible projective module, and hence, we have an epimorphism
$K(\lambda )$
is the image of a homomorphism from an admissible projective module, and hence, we have an epimorphism
![]() $\Delta (\lambda ) \twoheadrightarrow Q(\lambda )$
. Now, to complete the proof, we note that for any
$\Delta (\lambda ) \twoheadrightarrow Q(\lambda )$
. Now, to complete the proof, we note that for any
![]() $\mu \in {\Lambda (\zeta )}$
with
$\mu \in {\Lambda (\zeta )}$
with
![]() $\mu>\lambda $
,
$\mu>\lambda $
,
![]() $\operatorname {Hom}\nolimits _{{\mathcal {O}}}(P(\mu ), \Delta (\lambda ))=[\Delta (\lambda ):L(\mu )]=0$
by Theorem 14.
$\operatorname {Hom}\nolimits _{{\mathcal {O}}}(P(\mu ), \Delta (\lambda ))=[\Delta (\lambda ):L(\mu )]=0$
by Theorem 14.
For any
![]() $M\in \mathcal F(\Delta )$
, we denote by
$M\in \mathcal F(\Delta )$
, we denote by
![]() $(M : \Delta (\lambda ))$
the multiplicity of a standard object
$(M : \Delta (\lambda ))$
the multiplicity of a standard object
![]() $\Delta (\lambda )$
in a
$\Delta (\lambda )$
in a
![]() $\Delta $
-flag of M. The following corollary determines the multiplicities of standard objects of the projective cover in
$\Delta $
-flag of M. The following corollary determines the multiplicities of standard objects of the projective cover in
![]() ${\mathcal {O}}^{{\zeta }\text {-pres}}.$
${\mathcal {O}}^{{\zeta }\text {-pres}}.$
Corollary 16 (BGG reciprocity).
For any
![]() $\lambda ,\mu \in {\Lambda (\zeta )}$
, we have
$\lambda ,\mu \in {\Lambda (\zeta )}$
, we have
Proof. Let
![]() $\gamma \in \mathfrak {h}^\ast $
be an integral weight with
$\gamma \in \mathfrak {h}^\ast $
be an integral weight with
![]() $\gamma \not \in {\Lambda (\zeta )}$
. Then
$\gamma \not \in {\Lambda (\zeta )}$
. Then
![]() $\operatorname {Ind}\nolimits _{\mathfrak p}^{\mathfrak {g}} L_{\mathfrak l_\zeta }(\gamma )$
is
$\operatorname {Ind}\nolimits _{\mathfrak p}^{\mathfrak {g}} L_{\mathfrak l_\zeta }(\gamma )$
is
![]() $\alpha $
-finite for some
$\alpha $
-finite for some
![]() $\alpha \in \Pi _\zeta $
, which implies that
$\alpha \in \Pi _\zeta $
, which implies that
![]() $[\operatorname {Ind}\nolimits _{\mathfrak p}^{\mathfrak {g}} L_{\mathfrak l_\zeta }(\gamma ): L(\lambda )]=0$
since
$[\operatorname {Ind}\nolimits _{\mathfrak p}^{\mathfrak {g}} L_{\mathfrak l_\zeta }(\gamma ): L(\lambda )]=0$
since
![]() $L(\lambda )$
is
$L(\lambda )$
is
![]() $\alpha $
-free; see also Section 2.4. Therefore, for any
$\alpha $
-free; see also Section 2.4. Therefore, for any
![]() $w\in W_\zeta $
, we have
$w\in W_\zeta $
, we have
![]() $[M(w\cdot \mu )/M(\mu ):L(\lambda )]=0$
and hence
$[M(w\cdot \mu )/M(\mu ):L(\lambda )]=0$
and hence
By BGG reciprocity for category
![]() ${\mathcal {O}}$
, we have
${\mathcal {O}}$
, we have
![]() $(P(\lambda ): M(w\cdot \mu ))=(P(\lambda ):M(\mu ))$
. Finally, noting that the multiplicity of
$(P(\lambda ): M(w\cdot \mu ))=(P(\lambda ):M(\mu ))$
. Finally, noting that the multiplicity of
![]() $\overline \Delta (\mu )$
in a
$\overline \Delta (\mu )$
in a
![]() $\overline \Delta $
-flag of
$\overline \Delta $
-flag of
![]() $\Delta (\mu )$
is
$\Delta (\mu )$
is
![]() $|W_\zeta \cdot \mu |$
, the conclusion follows.
$|W_\zeta \cdot \mu |$
, the conclusion follows.
4.4. Tilting modules
In this subsection, we assume that
![]() $\mathfrak {g}$
is a basic Lie superalgebra (i.e.,
$\mathfrak {g}$
is a basic Lie superalgebra (i.e.,
![]() $\mathfrak {g}$
is one from (1.2) with
$\mathfrak {g}$
is one from (1.2) with
![]() $\mathfrak {g}\neq \mathfrak p(n)$
). There is a simple-preserving duality D on
$\mathfrak {g}\neq \mathfrak p(n)$
). There is a simple-preserving duality D on
![]() ${\mathcal {O}}$
; that is, D is a contravariant auto-equivalence such that
${\mathcal {O}}$
; that is, D is a contravariant auto-equivalence such that
![]() $D^2\cong {\text {Id}}$
and
$D^2\cong {\text {Id}}$
and
![]() $D(L(\lambda ))\cong L(\lambda )$
, for each
$D(L(\lambda ))\cong L(\lambda )$
, for each
![]() $\lambda \in \mathfrak h^\ast $
.
$\lambda \in \mathfrak h^\ast $
.
For
![]() $\lambda \in {\Lambda (\zeta )}$
, we define the co-standard object
$\lambda \in {\Lambda (\zeta )}$
, we define the co-standard object
![]() $\nabla (\lambda )$
for
$\nabla (\lambda )$
for
![]() ${\mathcal {O}}^{{\zeta }\text {-pres}}$
by
${\mathcal {O}}^{{\zeta }\text {-pres}}$
by
It follows from Proposition 7 that
![]() $\nabla (\lambda )\in {\mathcal {O}}^{\zeta \text {-pres}}$
; see also [Reference Mazorchuk and StroppelMSt, Corollary 2.11]. Similarly, we define co-standard object
$\nabla (\lambda )\in {\mathcal {O}}^{\zeta \text {-pres}}$
; see also [Reference Mazorchuk and StroppelMSt, Corollary 2.11]. Similarly, we define co-standard object
![]() $\nabla _0(\lambda )$
for
$\nabla _0(\lambda )$
for
![]() ${\mathcal {O}}^{\zeta \text {-pres}}_{\bar 0}$
. If
${\mathcal {O}}^{\zeta \text {-pres}}_{\bar 0}$
. If
![]() ${\mathcal {O}}^{{\zeta }\text {-pres}}={\mathcal {O}}$
, then we arrive at the usual definition of dual Verma modules.
${\mathcal {O}}^{{\zeta }\text {-pres}}={\mathcal {O}}$
, then we arrive at the usual definition of dual Verma modules.
A module
![]() $M\in {\mathcal {O}}^{\zeta \text {-pres}}$
is referred to as a tilting module if M has both a
$M\in {\mathcal {O}}^{\zeta \text {-pres}}$
is referred to as a tilting module if M has both a
![]() $\Delta $
-flag and a
$\Delta $
-flag and a
![]() $\nabla $
-flag. In the case that
$\nabla $
-flag. In the case that
![]() ${\mathcal {O}}^{{\zeta }\text {-pres}}={\mathcal {O}}$
, for each
${\mathcal {O}}^{{\zeta }\text {-pres}}={\mathcal {O}}$
, for each
![]() $\lambda \in \mathfrak h^\ast $
, there is a unique indecomposable tilting module of highest weight
$\lambda \in \mathfrak h^\ast $
, there is a unique indecomposable tilting module of highest weight
![]() $\lambda $
, which we denote by
$\lambda $
, which we denote by
![]() $T^{{\mathcal {O}}}(\lambda )$
; namely,
$T^{{\mathcal {O}}}(\lambda )$
; namely,
![]() $T^{{\mathcal {O}}}(\lambda )$
has both a Verma flag and a dual Verma flag; see, for example, [Reference BrundanBr1]. We also denote by
$T^{{\mathcal {O}}}(\lambda )$
has both a Verma flag and a dual Verma flag; see, for example, [Reference BrundanBr1]. We also denote by
![]() $T^{{\mathcal {O}}_{\bar 0}}(\lambda )$
the indecomposable tilting module of highest weight
$T^{{\mathcal {O}}_{\bar 0}}(\lambda )$
the indecomposable tilting module of highest weight
![]() $\lambda $
in
$\lambda $
in
![]() ${\mathcal {O}}_{\bar 0}$
.
${\mathcal {O}}_{\bar 0}$
.
In the case that
![]() $\mathfrak g=\mathfrak g_{\bar 0}$
, the classification of indecomposable tilting modules in
$\mathfrak g=\mathfrak g_{\bar 0}$
, the classification of indecomposable tilting modules in
![]() ${\mathcal {O}}^{\zeta \text {-pres}}_{\bar 0}$
is given in [Reference Futorny, König and MazorchukFKM, Section 6]; see also [Reference Mazorchuk and StroppelMSt, Section 5.4]. In particular, the list
${\mathcal {O}}^{\zeta \text {-pres}}_{\bar 0}$
is given in [Reference Futorny, König and MazorchukFKM, Section 6]; see also [Reference Mazorchuk and StroppelMSt, Section 5.4]. In particular, the list
![]() $\{T^{{\mathcal {O}}_{\bar 0}}(w_0^\zeta \cdot \lambda )|~\lambda \in {\Lambda (\zeta )}\}$
forms a complete set of non-isomorphic indecomposable tilting modules in
$\{T^{{\mathcal {O}}_{\bar 0}}(w_0^\zeta \cdot \lambda )|~\lambda \in {\Lambda (\zeta )}\}$
forms a complete set of non-isomorphic indecomposable tilting modules in
![]() ${\mathcal {O}}^{\zeta \text {-pres}}_{\bar 0}$
, and each
${\mathcal {O}}^{\zeta \text {-pres}}_{\bar 0}$
, and each
![]() $T_0(\lambda ):= T^{{\mathcal {O}}_{\bar 0}}(w_0^\zeta \cdot \lambda )$
is the unique indecomposable tilting module containing
$T_0(\lambda ):= T^{{\mathcal {O}}_{\bar 0}}(w_0^\zeta \cdot \lambda )$
is the unique indecomposable tilting module containing
![]() $\Delta _0(\lambda )$
such that
$\Delta _0(\lambda )$
such that
![]() $T_0(\lambda )/\Delta _0(\lambda )$
has a
$T_0(\lambda )/\Delta _0(\lambda )$
has a
![]() $\Delta _0$
-flag. Here, we recall that
$\Delta _0$
-flag. Here, we recall that
![]() $w_0^\zeta $
denotes the longest element in
$w_0^\zeta $
denotes the longest element in
![]() $W_\zeta $
. We set
$W_\zeta $
. We set
for each
![]() $\lambda \in {\Lambda (\zeta )}$
. Below we give a classification of indecomposable tilting objects in
$\lambda \in {\Lambda (\zeta )}$
. Below we give a classification of indecomposable tilting objects in
![]() ${\mathcal {O}}^{{\zeta }\text {-pres}}$
. We remark that the type I case was considered in [Reference Chen, Cheng and MazorchukCCM2, Section 6.1].
${\mathcal {O}}^{{\zeta }\text {-pres}}$
. We remark that the type I case was considered in [Reference Chen, Cheng and MazorchukCCM2, Section 6.1].
Proposition 17. The modules
![]() $\{T(\lambda )|~\lambda \in {\Lambda (\zeta )}\}$
constitute an exhaustive list of indecomposable tilting modules in
$\{T(\lambda )|~\lambda \in {\Lambda (\zeta )}\}$
constitute an exhaustive list of indecomposable tilting modules in
![]() ${\mathcal {O}}^{\zeta \text {-pres}}$
. In particular, each
${\mathcal {O}}^{\zeta \text {-pres}}$
. In particular, each
![]() $T(\lambda )$
is the unique indecomposable tilting module in
$T(\lambda )$
is the unique indecomposable tilting module in
![]() ${\mathcal {O}}^{{\zeta }\text {-pres}}$
containing
${\mathcal {O}}^{{\zeta }\text {-pres}}$
containing
![]() $\Delta (\lambda )$
such that
$\Delta (\lambda )$
such that
![]() $T(\lambda )/\Delta (\lambda )$
has a
$T(\lambda )/\Delta (\lambda )$
has a
![]() $\Delta $
-flag.
$\Delta $
-flag.
Proof. Let
![]() $\lambda \in \Lambda (\zeta )$
, and set
$\lambda \in \Lambda (\zeta )$
, and set
![]() $\mu =\lambda -2\rho _1\in \Lambda (\zeta )$
, where
$\mu =\lambda -2\rho _1\in \Lambda (\zeta )$
, where
![]() $\rho _1$
denotes the half-sum of roots in
$\rho _1$
denotes the half-sum of roots in
![]() $\mathfrak n^+_{\bar 1}$
. We have
$\mathfrak n^+_{\bar 1}$
. We have
Now,
![]() $P_{\mathfrak l_\zeta }(\mu )$
has an
$P_{\mathfrak l_\zeta }(\mu )$
has an
![]() ${\mathfrak l_\zeta }$
-Verma flag with highest term
${\mathfrak l_\zeta }$
-Verma flag with highest term
![]() $M_{\mathfrak l_\zeta }(w_0^\zeta \cdot \mu )$
, and hence,
$M_{\mathfrak l_\zeta }(w_0^\zeta \cdot \mu )$
, and hence,
![]() $U(\mathfrak n^+_{\bar 1})\otimes P_{\mathfrak l_\zeta }(\mu )$
has a
$U(\mathfrak n^+_{\bar 1})\otimes P_{\mathfrak l_\zeta }(\mu )$
has a
![]() ${\mathfrak l_\zeta }$
-Verma flag with highest term
${\mathfrak l_\zeta }$
-Verma flag with highest term
![]() $M_{\mathfrak l_\zeta }(w_0^\zeta \cdot \mu +2\rho _{1})=M_{\mathfrak l_\zeta }(w_0^\zeta \cdot \left (\mu +2\rho _{1}\right ))=M_{\mathfrak l_\zeta }(w_0^\zeta \cdot \lambda )$
. Therefore,
$M_{\mathfrak l_\zeta }(w_0^\zeta \cdot \mu +2\rho _{1})=M_{\mathfrak l_\zeta }(w_0^\zeta \cdot \left (\mu +2\rho _{1}\right ))=M_{\mathfrak l_\zeta }(w_0^\zeta \cdot \lambda )$
. Therefore,
![]() $\operatorname {Ind}\nolimits \Delta _0(\mu )$
has a Verma flag with highest term
$\operatorname {Ind}\nolimits \Delta _0(\mu )$
has a Verma flag with highest term
![]() $M(w_0^\zeta \cdot \lambda )$
. This implies that
$M(w_0^\zeta \cdot \lambda )$
. This implies that
![]() $\operatorname {Ind}\nolimits T_0(\mu )$
has a Verma flag with highest term
$\operatorname {Ind}\nolimits T_0(\mu )$
has a Verma flag with highest term
![]() $M(w_0^\zeta \cdot \lambda )$
and hence, by Lemma 10, a
$M(w_0^\zeta \cdot \lambda )$
and hence, by Lemma 10, a
![]() $\Delta $
-flag with
$\Delta $
-flag with
![]() $\Delta (\lambda )$
as a highest term. Therefore, the indecomposable direct summand of
$\Delta (\lambda )$
as a highest term. Therefore, the indecomposable direct summand of
![]() $\operatorname {Ind}\nolimits T_0(\mu )$
containing
$\operatorname {Ind}\nolimits T_0(\mu )$
containing
![]() $\Delta (\lambda )$
is (isomorphic to)
$\Delta (\lambda )$
is (isomorphic to)
![]() $T(\lambda )$
. By Proposition 13,
$T(\lambda )$
. By Proposition 13,
![]() $T(\lambda )$
has a
$T(\lambda )$
has a
![]() $\Delta $
-flag. Also, by Lemma 3,
$\Delta $
-flag. Also, by Lemma 3,
![]() $\operatorname {Ind}\nolimits T_0(\mu )\in {\mathcal {O}}^{\zeta \text {-pres}}$
, and therefore,
$\operatorname {Ind}\nolimits T_0(\mu )\in {\mathcal {O}}^{\zeta \text {-pres}}$
, and therefore,
![]() $T(\lambda )$
lies in
$T(\lambda )$
lies in
![]() ${\mathcal {O}}^{\zeta \text {-pres}}$
. Since
${\mathcal {O}}^{\zeta \text {-pres}}$
. Since
![]() $T(\lambda )$
is self-dual, it follows that
$T(\lambda )$
is self-dual, it follows that
![]() $T(\lambda )$
has both a
$T(\lambda )$
has both a
![]() $\Delta $
-flag and a
$\Delta $
-flag and a
![]() $\nabla $
-flag. Therefore,
$\nabla $
-flag. Therefore,
![]() $T(\lambda )$
is an indecomposable tilting module in
$T(\lambda )$
is an indecomposable tilting module in
![]() ${\mathcal {O}}^{\zeta \text {-pres}}.$
${\mathcal {O}}^{\zeta \text {-pres}}.$
Now, if T is an indecomposable tilting module in
![]() ${\mathcal {O}}^{\zeta \text {-pres}}$
with a
${\mathcal {O}}^{\zeta \text {-pres}}$
with a
![]() $\Delta $
-flag starting at
$\Delta $
-flag starting at
![]() $\Delta (\lambda )$
, then by uniqueness of tilting module (see, for example, [Reference SoergelSoe, Proposition 5.6]), we have
$\Delta (\lambda )$
, then by uniqueness of tilting module (see, for example, [Reference SoergelSoe, Proposition 5.6]), we have
![]() $T\cong T(\lambda )$
. This completes the proof.
$T\cong T(\lambda )$
. This completes the proof.
Corollary 18. (Ringel duality) For
![]() $\lambda ,\mu \in {\Lambda (\zeta )}$
, we have
$\lambda ,\mu \in {\Lambda (\zeta )}$
, we have
Proof. Let
![]() $\lambda ,\mu \in {\Lambda (\zeta )}$
. By (4.15), the BGG reciprocity and the Ringel-Soergel duality in
$\lambda ,\mu \in {\Lambda (\zeta )}$
. By (4.15), the BGG reciprocity and the Ringel-Soergel duality in
![]() ${\mathcal {O}}$
[Reference BrundanBr1] (see also [Reference Chen, Cheng and CoulembierCCC, Theorem 3.7]), we have
${\mathcal {O}}$
[Reference BrundanBr1] (see also [Reference Chen, Cheng and CoulembierCCC, Theorem 3.7]), we have
Thus, it follows from Proposition 17 that
 $$ \begin{align*} (T(\lambda):\Delta(\mu))=&(T^{{\mathcal{O}}}(w_0^\zeta\cdot\lambda):M(w_0^\zeta\cdot\mu))\\ =&[M(-w_0^\zeta\cdot\mu):L(-w_0^\zeta\cdot\lambda)] = [\overline{\Delta}(-w_0^\zeta\cdot\mu): L(-w_0^\zeta\cdot\lambda)]. \end{align*} $$
$$ \begin{align*} (T(\lambda):\Delta(\mu))=&(T^{{\mathcal{O}}}(w_0^\zeta\cdot\lambda):M(w_0^\zeta\cdot\mu))\\ =&[M(-w_0^\zeta\cdot\mu):L(-w_0^\zeta\cdot\lambda)] = [\overline{\Delta}(-w_0^\zeta\cdot\mu): L(-w_0^\zeta\cdot\lambda)]. \end{align*} $$
5.
 $\imath $
-Canonical bases on symmetrized Fock space
$\imath $
-Canonical bases on symmetrized Fock space
In this section, we introduce a quasi-split quantum symmetric pair
![]() $(U,U^\imath )$
of type
$(U,U^\imath )$
of type
![]() $AIII$
and study a q-symmetrized Fock space which carries an action of the
$AIII$
and study a q-symmetrized Fock space which carries an action of the
![]() $\imath $
-quantum group
$\imath $
-quantum group
![]() $U^\imath $
. We construct
$U^\imath $
. We construct
![]() $\imath $
-canonical and dual
$\imath $
-canonical and dual
![]() $\imath $
-canonical bases on this space. In Section 7.2, we shall relate these bases in a natural way to tilting and simple objects, respectively, in the category
$\imath $
-canonical bases on this space. In Section 7.2, we shall relate these bases in a natural way to tilting and simple objects, respectively, in the category
![]() $\mathcal W(\zeta )$
in the case when
$\mathcal W(\zeta )$
in the case when
![]() $\mathfrak {g}$
is an ortho-symplectic Lie superalgebra.
$\mathfrak {g}$
is an ortho-symplectic Lie superalgebra.
5.1. Quantum symmetric pair
 $(U,U^\imath )$
$(U,U^\imath )$
Let U denote the infinite-rank quantum group of type A with Chevalley generators
![]() $\{E_{\alpha _i},F_{\alpha _i},K^{\pm 1}_{\alpha _i}|i\in {\mathbb Z}\}$
(i.e., U is the associative algebra over
$\{E_{\alpha _i},F_{\alpha _i},K^{\pm 1}_{\alpha _i}|i\in {\mathbb Z}\}$
(i.e., U is the associative algebra over
![]() $\mathbb {Q}(q)$
generated by these generators subject to certain well-known relations; see, for example, [Reference Cheng, Lam and WangCLW, Section 2.1]). The anti-linear (
$\mathbb {Q}(q)$
generated by these generators subject to certain well-known relations; see, for example, [Reference Cheng, Lam and WangCLW, Section 2.1]). The anti-linear (
![]() $q\rightarrow q^{-1}$
) map
$q\rightarrow q^{-1}$
) map
![]() $\psi $
preserving
$\psi $
preserving
![]() $E_{\alpha _i}$
and
$E_{\alpha _i}$
and
![]() $F_{\alpha _i}$
and sending
$F_{\alpha _i}$
and sending
![]() $K_{\alpha _i}$
to
$K_{\alpha _i}$
to
![]() $K^{-1}_{\alpha _i}$
induces the well-known bar involution on U. The algebra U is a Hopf algebra with co-multiplication
$K^{-1}_{\alpha _i}$
induces the well-known bar involution on U. The algebra U is a Hopf algebra with co-multiplication
![]() $\Delta $
[Reference KashiwaraKas]:
$\Delta $
[Reference KashiwaraKas]:
 $$ \begin{align*} &\Delta(E_{\alpha_i})=1\otimes E_{\alpha_i}+E_{\alpha_i}\otimes K^{-1}_{\alpha_i},\\ &\Delta(F_{\alpha_i})=F_{\alpha_i}\otimes 1+K_{\alpha_i}\otimes F_{\alpha_i},\\ &\Delta(K_{\alpha_i})=K_{\alpha_i}\otimes K_{\alpha_i}. \end{align*} $$
$$ \begin{align*} &\Delta(E_{\alpha_i})=1\otimes E_{\alpha_i}+E_{\alpha_i}\otimes K^{-1}_{\alpha_i},\\ &\Delta(F_{\alpha_i})=F_{\alpha_i}\otimes 1+K_{\alpha_i}\otimes F_{\alpha_i},\\ &\Delta(K_{\alpha_i})=K_{\alpha_i}\otimes K_{\alpha_i}. \end{align*} $$
Now let
![]() $U^\imath $
be the associative algebra over
$U^\imath $
be the associative algebra over
![]() $\mathbb {Q}(q)$
generated by
$\mathbb {Q}(q)$
generated by
![]() $\{e_{\alpha _i},f_{\alpha _i},k^{\pm 1}_{\alpha _i},t|i>0\}$
subject to the relations in [Reference Bao and WangBW, Chapter 2.1]. Then, the anti-linear map
$\{e_{\alpha _i},f_{\alpha _i},k^{\pm 1}_{\alpha _i},t|i>0\}$
subject to the relations in [Reference Bao and WangBW, Chapter 2.1]. Then, the anti-linear map
![]() $\psi ^\imath $
that preserves the generators
$\psi ^\imath $
that preserves the generators
![]() $e_{\alpha _i},f_{\alpha _i},t$
, and that sends
$e_{\alpha _i},f_{\alpha _i},t$
, and that sends
![]() $k_{\alpha _i}$
to
$k_{\alpha _i}$
to
![]() $k^{-1}_{\alpha _i}$
, for
$k^{-1}_{\alpha _i}$
, for
![]() $i>0$
, defines an anti-linear involution on
$i>0$
, defines an anti-linear involution on
![]() $U^\imath $
.
$U^\imath $
.
According to [Reference Bao and WangBW, Proposition 2.2], there is an embedding of associative algebras
![]() $\imath :U^\imath \rightarrow U$
given by
$\imath :U^\imath \rightarrow U$
given by
 $$ \begin{align*} \imath(k_{\alpha_i})=K_{\alpha_i}K^{-1}_{\alpha_{-i}},\quad \imath(t)=E_{\alpha_0}+qF_{\alpha_0}K^{-1}_{\alpha_0}+K^{-1}_{\alpha_0},\\ \imath(e_{\alpha_i})=E_{\alpha_i}+K^{-1}_{\alpha_i}F_{\alpha_{-i}},\quad \imath(f_{\alpha_i})=F_{\alpha_i}K^{-1}_{\alpha_{-i}}+E_{\alpha_{-i}}, \end{align*} $$
$$ \begin{align*} \imath(k_{\alpha_i})=K_{\alpha_i}K^{-1}_{\alpha_{-i}},\quad \imath(t)=E_{\alpha_0}+qF_{\alpha_0}K^{-1}_{\alpha_0}+K^{-1}_{\alpha_0},\\ \imath(e_{\alpha_i})=E_{\alpha_i}+K^{-1}_{\alpha_i}F_{\alpha_{-i}},\quad \imath(f_{\alpha_i})=F_{\alpha_i}K^{-1}_{\alpha_{-i}}+E_{\alpha_{-i}}, \end{align*} $$
so that
![]() $U^\imath $
may be regarded as a subalgebra of U. We note that
$U^\imath $
may be regarded as a subalgebra of U. We note that
![]() $U^\imath $
is not a Hopf subalgebra, but rather a right coideal subalgebra of U. The pair
$U^\imath $
is not a Hopf subalgebra, but rather a right coideal subalgebra of U. The pair
![]() $(U,U^\imath )$
forms a quantum symmetric pair, in the sense of [Reference LetzterLe2], corresponding to a quasi-split symmetric pair of Satake type AIII. The subalgebra
$(U,U^\imath )$
forms a quantum symmetric pair, in the sense of [Reference LetzterLe2], corresponding to a quasi-split symmetric pair of Satake type AIII. The subalgebra
![]() $U^\imath $
is referred to as an
$U^\imath $
is referred to as an
![]() $\imath $
-quantum group.
$\imath $
-quantum group.
We observe that the involutions
![]() $\psi $
and
$\psi $
and
![]() $\psi ^\imath $
are not compatible with the embedding
$\psi ^\imath $
are not compatible with the embedding
![]() $\imath $
. However, there is a remarkable element
$\imath $
. However, there is a remarkable element
![]() $\Upsilon $
[Reference Bao and WangBW, Chapter 2.3] that lies in a certain topological completion of U and that intertwines these involutions in the following sense:
$\Upsilon $
[Reference Bao and WangBW, Chapter 2.3] that lies in a certain topological completion of U and that intertwines these involutions in the following sense:
This element
![]() $\Upsilon $
, referred to as the intertwiner, plays a crucial role in the Bao-Wang
$\Upsilon $
, referred to as the intertwiner, plays a crucial role in the Bao-Wang
![]() $\imath $
-canonical basis theory of quantum symmetric pairs.
$\imath $
-canonical basis theory of quantum symmetric pairs.
Following [Reference Bao and WangBW], a U-module equipped with an anti-linear bar involution compatible with the bar involution
![]() $\psi $
will be called a U-involutive module. We shall denote such an involution on the module also by
$\psi $
will be called a U-involutive module. We shall denote such an involution on the module also by
![]() $\psi $
. Similarly, a
$\psi $
. Similarly, a
![]() $U^\imath $
-involutive
$U^\imath $
-involutive
![]() $U^\imath $
-module is defined.
$U^\imath $
-module is defined.
Given a U-involutive module with involution
![]() $\psi $
, we can define
$\psi $
, we can define
It follows from (5.1) that M is
![]() $U^\imath $
-involutive with involution
$U^\imath $
-involutive with involution
![]() $\psi ^\imath $
. We note that the element
$\psi ^\imath $
. We note that the element
![]() $\Upsilon $
is invertible in a completion of U.
$\Upsilon $
is invertible in a completion of U.
5.2. Fock space
 $\mathbb {T}^{m|n}$
$\mathbb {T}^{m|n}$
Let
![]() $\mathbb {V}$
be the natural U-module with linear basis
$\mathbb {V}$
be the natural U-module with linear basis
![]() $v_r$
,
$v_r$
, ![]()
![]() . The action of U is given by
. The action of U is given by
Let
![]() $\mathbb {W}$
be the restricted dual with normalized dual basis
$\mathbb {W}$
be the restricted dual with normalized dual basis ![]() and U-action given by
and U-action given by
A fundamental property of Lusztig’s canonical basis theory for (finite rank) quantum groups is that tensor products of involutive modules can be made into involutive modules [Reference LusztigLu3, Chapter 27] by means of the quasi-
![]() $\mathcal R$
-matrix
$\mathcal R$
-matrix
![]() $\Theta $
[Reference LusztigLu3, Chapter 4]. (For the infinite-rank quantum group U, such a
$\Theta $
[Reference LusztigLu3, Chapter 4]. (For the infinite-rank quantum group U, such a
![]() $\Theta $
is constructed in [Reference Cheng, Lam and WangCLW, Section 3.1] based on [Reference LusztigLu3].) To be precise, for U-involutive U-modules M and N with involutions
$\Theta $
is constructed in [Reference Cheng, Lam and WangCLW, Section 3.1] based on [Reference LusztigLu3].) To be precise, for U-involutive U-modules M and N with involutions
![]() $\psi _M$
and
$\psi _M$
and
![]() $\psi _N$
, respectively, the U-module
$\psi _N$
, respectively, the U-module
![]() $M\otimes N$
is U-involutive with involution:
$M\otimes N$
is U-involutive with involution:
The U-modules
![]() $\mathbb {V}$
and
$\mathbb {V}$
and
![]() $\mathbb {W}$
are both U-involutive with anti-linear involutions
$\mathbb {W}$
are both U-involutive with anti-linear involutions
![]() $\psi _{\mathbb {V}}$
and
$\psi _{\mathbb {V}}$
and
![]() $\psi _{\mathbb {W}}$
determined by
$\psi _{\mathbb {W}}$
determined by
![]() $\psi _{\mathbb {V}}(v_r)=v_r$
and
$\psi _{\mathbb {V}}(v_r)=v_r$
and
![]() $\psi _{\mathbb {W}}(w_r)=w_r$
,
$\psi _{\mathbb {W}}(w_r)=w_r$
, ![]() , respectively. It follows, therefore, that the U-module
, respectively. It follows, therefore, that the U-module
![]() $\mathbb {T}^{m|n}:=\mathbb {V}^{\otimes m}\otimes \mathbb {W}^{\otimes n}$
, or rather a certain topological completion
$\mathbb {T}^{m|n}:=\mathbb {V}^{\otimes m}\otimes \mathbb {W}^{\otimes n}$
, or rather a certain topological completion
![]() $\widehat {\mathbb {T}}^{m|n}$
, is U-involutive. Using the formula (5.2), we can therefore make
$\widehat {\mathbb {T}}^{m|n}$
, is U-involutive. Using the formula (5.2), we can therefore make
![]() $\widehat {\mathbb {T}}^{m|n}$
into a
$\widehat {\mathbb {T}}^{m|n}$
into a
![]() $U^\imath $
-involutive
$U^\imath $
-involutive
![]() $U^\imath $
-module. We shall denote the involution on
$U^\imath $
-module. We shall denote the involution on
![]() $\widehat {\mathbb {T}}^{m|n}$
also by
$\widehat {\mathbb {T}}^{m|n}$
also by
![]() $\psi ^\imath $
so that we have
$\psi ^\imath $
so that we have
![]() $\psi ^\imath (uv)=\psi ^\imath (u)\psi ^\imath (v)$
, for
$\psi ^\imath (uv)=\psi ^\imath (u)\psi ^\imath (v)$
, for
![]() $u\in U^\imath $
and
$u\in U^\imath $
and
![]() $v\in \widehat {\mathbb {T}}^{m|n}$
.
$v\in \widehat {\mathbb {T}}^{m|n}$
.
5.3.
 $\imath $
-Canonical bases
$\imath $
-Canonical bases
Let
![]() $\mathbb {I}^{m|n}$
denote the set of functions from
$\mathbb {I}^{m|n}$
denote the set of functions from
![]() $\{1,2,\cdots ,m,\bar {1},\cdots ,\bar {n}\}$
to
$\{1,2,\cdots ,m,\bar {1},\cdots ,\bar {n}\}$
to ![]() . For each
. For each
![]() $f\in \mathbb {I}^{m|n}$
, we define
$f\in \mathbb {I}^{m|n}$
, we define
The set
![]() $\{M_f|f\in \mathbb {I}^{m|n}\}$
is a topological basis for
$\{M_f|f\in \mathbb {I}^{m|n}\}$
is a topological basis for
![]() $\widehat {\mathbb {T}}^{m|n}$
.
$\widehat {\mathbb {T}}^{m|n}$
.
We have a bijection between
![]() $\mathbb {I}_{m|n}$
and
$\mathbb {I}_{m|n}$
and
![]() $\Lambda ^{\texttt {int}}$
, the set of integer weights for the Lie superalgebra
$\Lambda ^{\texttt {int}}$
, the set of integer weights for the Lie superalgebra
![]() $\mathfrak {osp}(2m+1|2n)$
(see (6.1)). This bijection allows us to transfer notions that make sense for weights such as typical, dominant, anti-dominant, Bruhat order
$\mathfrak {osp}(2m+1|2n)$
(see (6.1)). This bijection allows us to transfer notions that make sense for weights such as typical, dominant, anti-dominant, Bruhat order
![]() $\succeq $
etc. to corresponding notions on
$\succeq $
etc. to corresponding notions on
![]() $\mathbb {I}_{m|n}$
. The precise bijection is not important for the subsequent discussion in this section. In this section, we shall only need the fact that the Bruhat order on weights induces a partial order
$\mathbb {I}_{m|n}$
. The precise bijection is not important for the subsequent discussion in this section. In this section, we shall only need the fact that the Bruhat order on weights induces a partial order
![]() $\succeq $
on
$\succeq $
on
![]() $\mathbb {I}_{m|n}$
.
$\mathbb {I}_{m|n}$
.
As we have seen earlier,
![]() $\mathbb {T}^{m|n}$
is a
$\mathbb {T}^{m|n}$
is a
![]() $U^\imath $
-involutive
$U^\imath $
-involutive
![]() $U^\imath $
-module. Recall that we have a right action of the Hecke algebra
$U^\imath $
-module. Recall that we have a right action of the Hecke algebra
![]() $\mathcal H_{B_m}$
(corresponding to the Weyl group
$\mathcal H_{B_m}$
(corresponding to the Weyl group
![]() $W_{B_m}$
of the Lie algebra of type
$W_{B_m}$
of the Lie algebra of type
![]() $B_m$
) on
$B_m$
) on
![]() $\mathbb {V}^{\otimes m}$
(see, for example, [Reference Bao and WangBW, (5.2)] for the explicit action). According to [Reference Bao and WangBW, Theorem 5.8], this action commutes with the action of
$\mathbb {V}^{\otimes m}$
(see, for example, [Reference Bao and WangBW, (5.2)] for the explicit action). According to [Reference Bao and WangBW, Theorem 5.8], this action commutes with the action of
![]() $U^\imath $
on
$U^\imath $
on
![]() $\mathbb {V}^{\otimes m}$
. There is also a right action of the Hecke algebra
$\mathbb {V}^{\otimes m}$
. There is also a right action of the Hecke algebra
![]() $\mathcal H_{A_n}$
(corresponding to the symmetric group
$\mathcal H_{A_n}$
(corresponding to the symmetric group
![]() $\mathfrak S_n$
) on
$\mathfrak S_n$
) on
![]() $\mathbb {W}^{\otimes n}$
(see, for example, [Reference Cheng, Lam and WangCLW, (2.9)]) that commutes with the action of U by [Reference JimboJi, Proposition 3]. We recall that Hecke algebras have natural anti-linear bar involutions determined by
$\mathbb {W}^{\otimes n}$
(see, for example, [Reference Cheng, Lam and WangCLW, (2.9)]) that commutes with the action of U by [Reference JimboJi, Proposition 3]. We recall that Hecke algebras have natural anti-linear bar involutions determined by
![]() $\overline {H}_i:=H_i^{-1}$
, where the
$\overline {H}_i:=H_i^{-1}$
, where the
![]() $H_i$
are the usual generators satisfying
$H_i$
are the usual generators satisfying
![]() $(H_i-q^{-1})(H_i+q)=0$
and the corresponding braid relations. Furthermore, in [Reference Bao and WangBW, Theorem 5.8] and [Reference JimboJi, Proposition 3], it is shown that the involutive module structures on
$(H_i-q^{-1})(H_i+q)=0$
and the corresponding braid relations. Furthermore, in [Reference Bao and WangBW, Theorem 5.8] and [Reference JimboJi, Proposition 3], it is shown that the involutive module structures on
![]() $\mathbb {V}^{\otimes m}$
and
$\mathbb {V}^{\otimes m}$
and
![]() $\mathbb {W}^{\otimes n}$
are compatible with the bar involutions on the respective Hecke algebras. We have the following.
$\mathbb {W}^{\otimes n}$
are compatible with the bar involutions on the respective Hecke algebras. We have the following.
Proposition 19. The action of
![]() $U^\imath $
and that of
$U^\imath $
and that of
![]() $\mathcal H_{B_m}\times \mathcal H_{A_n}$
on
$\mathcal H_{B_m}\times \mathcal H_{A_n}$
on
![]() $\mathbb {T}^{m|n}$
commute with each other. Furthermore, these actions are compatible with their respective involutions; that is, we have for
$\mathbb {T}^{m|n}$
commute with each other. Furthermore, these actions are compatible with their respective involutions; that is, we have for
![]() $u\in U^\imath $
,
$u\in U^\imath $
,
![]() $t\in \mathbb {T}^{m|n}$
, and
$t\in \mathbb {T}^{m|n}$
, and
![]() $H\in \mathcal H_{B_m}\times \mathcal H_{A_n}$
:
$H\in \mathcal H_{B_m}\times \mathcal H_{A_n}$
:
Proof. Let
![]() $x\in \mathbb V^{\otimes m}$
,
$x\in \mathbb V^{\otimes m}$
,
![]() $y\in \mathbb W^{\otimes n}$
,
$y\in \mathbb W^{\otimes n}$
,
![]() $u\in U^\imath $
,
$u\in U^\imath $
,
![]() $h_1\in \mathcal H_{B_m}$
and
$h_1\in \mathcal H_{B_m}$
and
![]() $h_2\in \mathcal H_{A_n}$
. We have
$h_2\in \mathcal H_{A_n}$
. We have
![]() $\Delta (u)=\sum _{i}u_1^i\otimes u_2^i$
, with
$\Delta (u)=\sum _{i}u_1^i\otimes u_2^i$
, with
![]() $u_1^i\in U^\imath $
and
$u_1^i\in U^\imath $
and
![]() $u_2^i\in U$
. We have
$u_2^i\in U$
. We have
 $$ \begin{align*} \left(\Delta(u)(x\otimes y)\right)(h_1\otimes h_2)&=\left(\sum_i u_1^i x\otimes u_2^i y\right)(h_1\otimes h_2) =\sum_i \left(u_1^i x\right)h_1\otimes \left(u_2^i y\right)h_2\\ &= \sum_iu_1^i \left(xh_1\right)\otimes u_2^i \left(yh_2\right) = \Delta(u)\left((x\otimes y)(h_1\otimes h_2)\right), \end{align*} $$
$$ \begin{align*} \left(\Delta(u)(x\otimes y)\right)(h_1\otimes h_2)&=\left(\sum_i u_1^i x\otimes u_2^i y\right)(h_1\otimes h_2) =\sum_i \left(u_1^i x\right)h_1\otimes \left(u_2^i y\right)h_2\\ &= \sum_iu_1^i \left(xh_1\right)\otimes u_2^i \left(yh_2\right) = \Delta(u)\left((x\otimes y)(h_1\otimes h_2)\right), \end{align*} $$
where the penultimate identity above follows from [Reference Bao and WangBW, Theorem 5.8] and [Reference JimboJi, Proposition 3]. This implies that the actions of
![]() $U^\imath $
and
$U^\imath $
and
![]() $\mathcal H_{B_m}\otimes \mathcal H_{A_n}$
on
$\mathcal H_{B_m}\otimes \mathcal H_{A_n}$
on
![]() $\mathbb {T}^{m|n}$
commute.
$\mathbb {T}^{m|n}$
commute.
By [Reference Bao and WangBW, Proposition 3.7 and Remark 3.14], the involution
![]() $\psi ^\imath $
on
$\psi ^\imath $
on
![]() $\mathbb {T}^{m|n}$
can be written in the following form as an involution on the tensor product of the
$\mathbb {T}^{m|n}$
can be written in the following form as an involution on the tensor product of the
![]() $U^\imath $
-involutive module
$U^\imath $
-involutive module
![]() $\mathbb V^{\otimes m}$
and the U-involutive module
$\mathbb V^{\otimes m}$
and the U-involutive module
![]() $\mathbb W^{\otimes n}$
using the quasi-
$\mathbb W^{\otimes n}$
using the quasi-
![]() $\mathcal K$
-matrix
$\mathcal K$
-matrix
![]() $\Theta ^\imath $
:
$\Theta ^\imath $
:
where
![]() $\Theta ^\imath :=\Delta (\Upsilon )\Theta (\Upsilon ^{-1}\otimes 1)$
. It is shown in [Reference Bao and WangBW, Chapter 3.3] that
$\Theta ^\imath :=\Delta (\Upsilon )\Theta (\Upsilon ^{-1}\otimes 1)$
. It is shown in [Reference Bao and WangBW, Chapter 3.3] that
![]() $\Theta ^\imath $
is an element in (the completion of)
$\Theta ^\imath $
is an element in (the completion of)
![]() $U^\imath \otimes U$
. We shall write
$U^\imath \otimes U$
. We shall write
![]() $\Theta ^\imath =\sum _i \theta _1^i\otimes \theta _2^i$
, with
$\Theta ^\imath =\sum _i \theta _1^i\otimes \theta _2^i$
, with
![]() $\theta _1^i\in U^\imath $
and
$\theta _1^i\in U^\imath $
and
![]() $\theta _2^i\in U$
.
$\theta _2^i\in U$
.
Now, for
![]() $u\in U^\imath $
, we have clearly
$u\in U^\imath $
, we have clearly
![]() $\psi ^\imath (u\cdot x\otimes y)=\psi ^\imath (u)\cdot \psi ^\imath (x\otimes y)$
, since
$\psi ^\imath (u\cdot x\otimes y)=\psi ^\imath (u)\cdot \psi ^\imath (x\otimes y)$
, since
![]() $\mathbb {T}^{m|n}$
is a
$\mathbb {T}^{m|n}$
is a
![]() $U^\imath $
-involutive module by [Reference Bao and WangBW, Proposition 3.13].
$U^\imath $
-involutive module by [Reference Bao and WangBW, Proposition 3.13].
However, for x, y,
![]() $h_1$
and
$h_1$
and
![]() $h_2$
as above, we have, again using [Reference Bao and WangBW, Theorem 5.8] and [Reference JimboJi, Proposition 3], the following:
$h_2$
as above, we have, again using [Reference Bao and WangBW, Theorem 5.8] and [Reference JimboJi, Proposition 3], the following:
 $$ \begin{align*} \psi^\imath\left(\left(x\otimes y\right)\left(h_1\otimes h_2\right)\right)&=\Theta^\imath\left(\psi^\imath(xh_1)\otimes\psi(yh_2)\right) = \Theta^\imath\left(\psi^\imath(x)\overline{h}_1\otimes\psi(y)\overline{h}_2\right)\\ =\sum_i &\theta_1^i(\psi^\imath(x)\overline{h}_1)\otimes\theta_2^i(\psi(y)\overline{h}_2) = \sum_i \left(\theta_1^i\psi^\imath(x)\right)\overline{h}_1\otimes\left(\theta_2^i\psi(y)\right)\overline{h}_2\\ =\Theta^\imath&\left(\psi^\imath(x)\otimes\psi(y)\right)(\overline{h}_1\otimes\overline{h}_2) = \psi^\imath\left(x\otimes y\right)(\overline{h}_1\otimes\overline{h}_2). \end{align*} $$
$$ \begin{align*} \psi^\imath\left(\left(x\otimes y\right)\left(h_1\otimes h_2\right)\right)&=\Theta^\imath\left(\psi^\imath(xh_1)\otimes\psi(yh_2)\right) = \Theta^\imath\left(\psi^\imath(x)\overline{h}_1\otimes\psi(y)\overline{h}_2\right)\\ =\sum_i &\theta_1^i(\psi^\imath(x)\overline{h}_1)\otimes\theta_2^i(\psi(y)\overline{h}_2) = \sum_i \left(\theta_1^i\psi^\imath(x)\right)\overline{h}_1\otimes\left(\theta_2^i\psi(y)\right)\overline{h}_2\\ =\Theta^\imath&\left(\psi^\imath(x)\otimes\psi(y)\right)(\overline{h}_1\otimes\overline{h}_2) = \psi^\imath\left(x\otimes y\right)(\overline{h}_1\otimes\overline{h}_2). \end{align*} $$
This concludes the proof.
One has the following important property of the involution
![]() $\psi ^\imath :\widehat {\mathbb {T}}^{m|n}\rightarrow \widehat {\mathbb {T}}^{m|n}$
[Reference Bao and WangBW, Lemma 9.7]:
$\psi ^\imath :\widehat {\mathbb {T}}^{m|n}\rightarrow \widehat {\mathbb {T}}^{m|n}$
[Reference Bao and WangBW, Lemma 9.7]:
 $$ \begin{align*} \psi^\imath(v_f)\in v_f+\sum_{g\prec f}{\mathbb Z}[q,q^{-1}]v_g\subseteq \widehat{\mathbb{T}}^{m|n}. \end{align*} $$
$$ \begin{align*} \psi^\imath(v_f)\in v_f+\sum_{g\prec f}{\mathbb Z}[q,q^{-1}]v_g\subseteq \widehat{\mathbb{T}}^{m|n}. \end{align*} $$
Since the partial order
![]() $\preceq $
satisfies the finite interval property by [Reference Bao and WangBW, Lemma 8.4], we can apply [Reference LusztigLu3, Lemma 24.2.1] and conclude the existence of
$\preceq $
satisfies the finite interval property by [Reference Bao and WangBW, Lemma 8.4], we can apply [Reference LusztigLu3, Lemma 24.2.1] and conclude the existence of
![]() $\psi ^\imath $
-invariant bases:
$\psi ^\imath $
-invariant bases:
Proposition 20. There exist unique
![]() $\psi ^\imath $
-invariant bases
$\psi ^\imath $
-invariant bases
![]() $\{T_f|f\in \mathbb {I}^{m|n}\}$
and
$\{T_f|f\in \mathbb {I}^{m|n}\}$
and
![]() $\{L_f|f\in \mathbb {I}^{m|n}\}$
of the form
$\{L_f|f\in \mathbb {I}^{m|n}\}$
of the form
 $$ \begin{align*} &T_f=M_f+\sum_{g\prec f}t_{gf}(q)M_g,\quad t_{gf}(q)\in q{\mathbb Z}[q],\\ &L_f=M_f+\sum_{g\prec f}\ell_{gf}(q)M_g,\quad\ell_{gf}(q)\in q^{-1}{\mathbb Z}[q^{-1}]. \end{align*} $$
$$ \begin{align*} &T_f=M_f+\sum_{g\prec f}t_{gf}(q)M_g,\quad t_{gf}(q)\in q{\mathbb Z}[q],\\ &L_f=M_f+\sum_{g\prec f}\ell_{gf}(q)M_g,\quad\ell_{gf}(q)\in q^{-1}{\mathbb Z}[q^{-1}]. \end{align*} $$
We set
![]() $t_{ff}=\ell _{ff}=1$
and
$t_{ff}=\ell _{ff}=1$
and
![]() $t_{gf}=\ell _{gf}=0$
, for
$t_{gf}=\ell _{gf}=0$
, for
![]() $g\not \preceq f$
.
$g\not \preceq f$
.
5.4. q-symmetric tensors
For a finite Weyl group W of a simple Lie algebra, we recall the well-known Chevalley-Solomon formula [Reference SolomonSol, Corollary 2.3]:
 $$ \begin{align*} \sum_{\tau\in W}q^{\ell(\tau)}=\prod_{i=1}^r\left(1+q+\cdots+q^{e_i}\right), \end{align*} $$
$$ \begin{align*} \sum_{\tau\in W}q^{\ell(\tau)}=\prod_{i=1}^r\left(1+q+\cdots+q^{e_i}\right), \end{align*} $$
where r is the rank of W and
![]() $e_1,\cdots ,e_r$
are the exponents of the corresponding Lie algebra. This implies the following formula:
$e_1,\cdots ,e_r$
are the exponents of the corresponding Lie algebra. This implies the following formula:
 $$ \begin{align*} \sum_{\tau\in W}q^{\ell(w_0)-\ell(\tau)}=\prod_{i=1}^r[e_i+1], \end{align*} $$
$$ \begin{align*} \sum_{\tau\in W}q^{\ell(w_0)-\ell(\tau)}=\prod_{i=1}^r[e_i+1], \end{align*} $$
where
![]() $[s]$
is the quantum integer
$[s]$
is the quantum integer
![]() $\frac {q^s-q^{-s}}{q-q^{-1}}$
, for
$\frac {q^s-q^{-s}}{q-q^{-1}}$
, for
![]() $s\in \mathbb {N}$
. We shall write
$s\in \mathbb {N}$
. We shall write
![]() $[W]:=\prod _{i=1}^r[e_i+1]$
. Now, suppose that W is a Weyl group of a reductive Lie algebra so that
$[W]:=\prod _{i=1}^r[e_i+1]$
. Now, suppose that W is a Weyl group of a reductive Lie algebra so that
![]() $W=W^1\times \cdots \times W^t$
, where each
$W=W^1\times \cdots \times W^t$
, where each
![]() $W^j$
,
$W^j$
,
![]() $1\le j\le t$
, is a Weyl group of a simple Lie algebra. We shall use the following notation:
$1\le j\le t$
, is a Weyl group of a simple Lie algebra. We shall use the following notation:
 $$ \begin{align*} [W]:=\prod_{j=1}^t[W^j]. \end{align*} $$
$$ \begin{align*} [W]:=\prod_{j=1}^t[W^j]. \end{align*} $$
Let
![]() $W_\zeta $
be a (parabolic) subgroup of
$W_\zeta $
be a (parabolic) subgroup of
![]() $W_{B_m}\times \mathfrak {S}_n$
generated by simple reflections. Indeed,
$W_{B_m}\times \mathfrak {S}_n$
generated by simple reflections. Indeed,
![]() $W_\zeta $
is a product of Weyl groups of the form
$W_\zeta $
is a product of Weyl groups of the form
![]() $W_\zeta = W^1\times \cdots \times W^s\times W^{s+1}\times \cdots \times W^{s+t}$
, where
$W_\zeta = W^1\times \cdots \times W^s\times W^{s+1}\times \cdots \times W^{s+t}$
, where
![]() $W^1$
is either of type A or B, and the remaining
$W^1$
is either of type A or B, and the remaining
![]() $W^i$
s are all of type A. Furthermore, the sum of the ranks of the
$W^i$
s are all of type A. Furthermore, the sum of the ranks of the
![]() $W^i$
s,
$W^i$
s,
![]() $i=1,\cdots ,s$
(respectively,
$i=1,\cdots ,s$
(respectively,
![]() $i=s+1,\cdots ,s+t$
) equals m (respectively, equals n). Let
$i=s+1,\cdots ,s+t$
) equals m (respectively, equals n). Let
![]() $\mathcal H_\zeta $
be the Hecke subalgebra of the Hecke algebra
$\mathcal H_\zeta $
be the Hecke subalgebra of the Hecke algebra
![]() $\mathcal {H}_{B_m}\times \mathcal H_{A_n}$
associated with
$\mathcal {H}_{B_m}\times \mathcal H_{A_n}$
associated with
![]() $W_\zeta $
. Let
$W_\zeta $
. Let
 $$ \begin{align} S_\zeta:=\sum_{\sigma\in W_\zeta} q^{\ell(w_0^\zeta)-\ell(\sigma)}H_\sigma = \prod_{i=1}^{s+t}S_i, \end{align} $$
$$ \begin{align} S_\zeta:=\sum_{\sigma\in W_\zeta} q^{\ell(w_0^\zeta)-\ell(\sigma)}H_\sigma = \prod_{i=1}^{s+t}S_i, \end{align} $$
where
![]() $w_0^\zeta $
is the longest element in
$w_0^\zeta $
is the longest element in
![]() $W_\zeta $
,
$W_\zeta $
,
![]() $S_i=\sum _{\tau \in W^i} q^{\ell (w_0^i)-\ell (\tau )}H_\tau $
, and
$S_i=\sum _{\tau \in W^i} q^{\ell (w_0^i)-\ell (\tau )}H_\tau $
, and
![]() $w_0^i$
is the longest element in
$w_0^i$
is the longest element in
![]() $W^i$
. The bar involution on
$W^i$
. The bar involution on
![]() $\mathcal {H}_{B_m}\times \mathcal H_{A_n}$
restricts to the bar involution on
$\mathcal {H}_{B_m}\times \mathcal H_{A_n}$
restricts to the bar involution on
![]() $\mathcal {H}_\zeta $
, and we have that
$\mathcal {H}_\zeta $
, and we have that
 $$ \begin{align*} \overline{S_i}=S_i\quad \text{and}\quad S_i H_\tau=q^{-\ell(\tau)}S_i=H_\tau S_i ,\ \tau\in W^i,\\ \overline{S_\zeta}=S_\zeta\quad \text{and}\quad S_\zeta H_\sigma=q^{-\ell(\sigma)}S_\zeta=H_\sigma S_\zeta ,\ \sigma\in W_\zeta. \end{align*} $$
$$ \begin{align*} \overline{S_i}=S_i\quad \text{and}\quad S_i H_\tau=q^{-\ell(\tau)}S_i=H_\tau S_i ,\ \tau\in W^i,\\ \overline{S_\zeta}=S_\zeta\quad \text{and}\quad S_\zeta H_\sigma=q^{-\ell(\sigma)}S_\zeta=H_\sigma S_\zeta ,\ \sigma\in W_\zeta. \end{align*} $$
Consider the following
![]() $\mathbb {Q}(q)$
-linear subspace of
$\mathbb {Q}(q)$
-linear subspace of
![]() $\mathbb {T}^{m|n}$
:
$\mathbb {T}^{m|n}$
:
Then
![]() $\mathbb T^{m|n} S_\zeta $
is a
$\mathbb T^{m|n} S_\zeta $
is a
![]() $U^\imath $
-submodule by Proposition 19. Let
$U^\imath $
-submodule by Proposition 19. Let
![]() $\mathbb {I}^{m|n}_{\zeta -}$
denote the set of elements in
$\mathbb {I}^{m|n}_{\zeta -}$
denote the set of elements in
![]() $\mathbb {I}^{m|n}$
that are anti-dominant with respect to
$\mathbb {I}^{m|n}$
that are anti-dominant with respect to
![]() $W_\zeta $
. For
$W_\zeta $
. For
![]() $f\in {\mathbb Z}^{m|n}_{\zeta -}$
, we let
$f\in {\mathbb Z}^{m|n}_{\zeta -}$
, we let
![]() $W_f:=\{\sigma \in W_\zeta |f\cdot \sigma =f\}$
be the stabilizer subgroup inside
$W_f:=\{\sigma \in W_\zeta |f\cdot \sigma =f\}$
be the stabilizer subgroup inside
![]() $W_\zeta $
and
$W_\zeta $
and
![]() $W^f$
the set of shortest length representatives of the coset
$W^f$
the set of shortest length representatives of the coset
![]() $W_f\backslash W_\zeta $
.
$W_f\backslash W_\zeta $
.
Define the following sets of monomial bases for
![]() $\mathbb T^{m|n}_\zeta $
:
$\mathbb T^{m|n}_\zeta $
:
From the formulas of the action of the Hecke algebra on
![]() $M_f$
, it follows that the basis elements
$M_f$
, it follows that the basis elements
![]() $\widetilde {N}_f$
lie in the
$\widetilde {N}_f$
lie in the
![]() ${\mathbb Z}[q,q^{-1}]$
-span of
${\mathbb Z}[q,q^{-1}]$
-span of
![]() $\{M_g|g\in \mathbb {I}^{m|n}\}$
. The
$\{M_g|g\in \mathbb {I}^{m|n}\}$
. The
![]() $\widetilde {M}_f$
s also lie in the
$\widetilde {M}_f$
s also lie in the
![]() ${\mathbb Z}[q,q^{-1}]$
-span of
${\mathbb Z}[q,q^{-1}]$
-span of
![]() $\{M_g|g\in \mathbb {I}^{m|n}\}$
, which can be seen as follows. Suppose that the Hecke algebra of
$\{M_g|g\in \mathbb {I}^{m|n}\}$
, which can be seen as follows. Suppose that the Hecke algebra of
![]() $W^i$
acts on
$W^i$
acts on
![]() $\mathbb V^{\otimes m_i}$
, for
$\mathbb V^{\otimes m_i}$
, for
![]() $i=1,\cdots ,s$
, and the Hecke algebra of
$i=1,\cdots ,s$
, and the Hecke algebra of
![]() $W^j$
acts on
$W^j$
acts on
![]() $\mathbb W^{\otimes n_{j}}$
,
$\mathbb W^{\otimes n_{j}}$
,
![]() $j=s+1,\cdots ,s+t$
. We have
$j=s+1,\cdots ,s+t$
. We have
![]() $\sum _{i}m_i=m$
and
$\sum _{i}m_i=m$
and
![]() $\sum _{j}n_j=n$
. The element
$\sum _{j}n_j=n$
. The element
where
![]() $f_i$
is f restricted to the interval corresponding to
$f_i$
is f restricted to the interval corresponding to
![]() $W^i$
, is an
$W^i$
, is an
![]() $\imath $
-canonical basis element for
$\imath $
-canonical basis element for
![]() $i=1$
and a canonical basis element for
$i=1$
and a canonical basis element for
![]() $i>1$
. Thus, by [Reference Bao and WangBW, Theorem 4.20] in the case of
$i>1$
. Thus, by [Reference Bao and WangBW, Theorem 4.20] in the case of
![]() $i=1$
and [Reference LusztigLu3, Theorem 27.3.2] in the case
$i=1$
and [Reference LusztigLu3, Theorem 27.3.2] in the case
![]() $i>1$
, it lies in the
$i>1$
, it lies in the
![]() ${\mathbb Z}[q,q^{-1}]$
-span of corresponding
${\mathbb Z}[q,q^{-1}]$
-span of corresponding
![]() $M_{g_i}$
, where the notation of
$M_{g_i}$
, where the notation of
![]() $g_i$
is self-explanatory. Now, we have
$g_i$
is self-explanatory. Now, we have
and hence, it lies in the
![]() ${\mathbb Z}[q,q^{-1}]$
-span of
${\mathbb Z}[q,q^{-1}]$
-span of
![]() $M_{g}$
,
$M_{g}$
,
![]() $g\in \mathbb {I}^{m|n}$
.
$g\in \mathbb {I}^{m|n}$
.
For
![]() $f\in {\mathbb Z}^{m|n}_{\zeta -}$
, we also define
$f\in {\mathbb Z}^{m|n}_{\zeta -}$
, we also define
 $$ \begin{align} N_f:=\frac{[W_\zeta]}{[W_f]}\widetilde{N}_f. \end{align} $$
$$ \begin{align} N_f:=\frac{[W_\zeta]}{[W_f]}\widetilde{N}_f. \end{align} $$
Suppose that
![]() $f\in \mathbb {I}^{m|n}$
, but not necessarily in
$f\in \mathbb {I}^{m|n}$
, but not necessarily in
![]() $\mathbb {I}^{m|n}_{\zeta -}$
. Let
$\mathbb {I}^{m|n}_{\zeta -}$
. Let
![]() $\tau \in W_\zeta $
be of shortest length such that
$\tau \in W_\zeta $
be of shortest length such that
![]() $f\cdot \tau \in \mathbb {I}^{m|n}_{\zeta -}$
. Then we have
$f\cdot \tau \in \mathbb {I}^{m|n}_{\zeta -}$
. Then we have
Similarly, we have the identity
![]() $\frac {1}{[W_f]}M_f S_\zeta =q^{-\ell (\tau )}\widetilde {M}_{f\cdot \tau }$
.
$\frac {1}{[W_f]}M_f S_\zeta =q^{-\ell (\tau )}\widetilde {M}_{f\cdot \tau }$
.
Lemma 21. The bar involution on
![]() $\widehat {\mathbb T}^{m|n}$
restricts to a bar involution on
$\widehat {\mathbb T}^{m|n}$
restricts to a bar involution on
![]() $\widehat {\mathbb T}^{m|n}_\zeta $
such that, for
$\widehat {\mathbb T}^{m|n}_\zeta $
such that, for
![]() $f\in {\mathbb Z}^{m|n}_{\zeta -}$
, we have the following:
$f\in {\mathbb Z}^{m|n}_{\zeta -}$
, we have the following:
-
(1)
 $\psi ^\imath \left ({\widetilde {N}}_f\right )\in \widetilde {N}_f+\sum _{g\prec f}{\mathbb Z}[q,q^{-1}] \widetilde {N}_g$
,
$\psi ^\imath \left ({\widetilde {N}}_f\right )\in \widetilde {N}_f+\sum _{g\prec f}{\mathbb Z}[q,q^{-1}] \widetilde {N}_g$
, -
(2)
 $\psi ^\imath \left ({\widetilde {M}}_f\right )\in \widetilde {M}_f+\sum _{g\prec f}{\mathbb Z}[q,q^{-1}] \widetilde {M}_g$
,
$\psi ^\imath \left ({\widetilde {M}}_f\right )\in \widetilde {M}_f+\sum _{g\prec f}{\mathbb Z}[q,q^{-1}] \widetilde {M}_g$
, -
(3)
 $\psi ^\imath \left ({N}_f\right )\in {N}_f+\sum _{g\prec f}{\mathbb Z}[q,q^{-1}] {N}_g.$
$\psi ^\imath \left ({N}_f\right )\in {N}_f+\sum _{g\prec f}{\mathbb Z}[q,q^{-1}] {N}_g.$
Proof. For
![]() $f\in \mathbb {I}^{m|n}_{\zeta -}$
, suppose that
$f\in \mathbb {I}^{m|n}_{\zeta -}$
, suppose that
![]() $\psi ^\imath (M_f) = M_f+\sum _{g\prec f}r_{gf}M_g$
with
$\psi ^\imath (M_f) = M_f+\sum _{g\prec f}r_{gf}M_g$
with
![]() $r_{gf}\in {\mathbb Z}[q,q^{-1}]$
. Then, by Proposition 19 and (5.8), we have
$r_{gf}\in {\mathbb Z}[q,q^{-1}]$
. Then, by Proposition 19 and (5.8), we have
 $$ \begin{align*} \psi^\imath({\widetilde{N}}_f)&=\psi^\imath({M_f S_\zeta})=\psi^\imath({M}_f) S_\zeta = M_fS_\zeta+\sum_{g\prec f}r_{gf}M_gS_\zeta =\widetilde{N}_f + \sum_{g\prec f; g\in\mathbb{I}^{m|n}_{\zeta -}}r^{\prime}_{gf} \widetilde{N}_g. \end{align*} $$
$$ \begin{align*} \psi^\imath({\widetilde{N}}_f)&=\psi^\imath({M_f S_\zeta})=\psi^\imath({M}_f) S_\zeta = M_fS_\zeta+\sum_{g\prec f}r_{gf}M_gS_\zeta =\widetilde{N}_f + \sum_{g\prec f; g\in\mathbb{I}^{m|n}_{\zeta -}}r^{\prime}_{gf} \widetilde{N}_g. \end{align*} $$
Since
![]() $r_{gf}\in {\mathbb Z}[q,q^{-1}]$
, we have
$r_{gf}\in {\mathbb Z}[q,q^{-1}]$
, we have
![]() $r^{\prime }_{fg}\in {\mathbb Z}[q,q^{-1}]$
by (5.8). This proves Part (1).
$r^{\prime }_{fg}\in {\mathbb Z}[q,q^{-1}]$
by (5.8). This proves Part (1).
We know that each
![]() $\widetilde {M}_f$
is a decomposable tensor, where the first factor is either an
$\widetilde {M}_f$
is a decomposable tensor, where the first factor is either an
![]() $\imath $
-canonical or canonical basis element and the remaining ones are canonical basis elements in the respective tensor powers of either
$\imath $
-canonical or canonical basis element and the remaining ones are canonical basis elements in the respective tensor powers of either
![]() $\mathbb V$
or
$\mathbb V$
or
![]() $\mathbb W$
. Recalling the definition of bar involution
$\mathbb W$
. Recalling the definition of bar involution
![]() $\psi ^\imath $
on a tensor product of a
$\psi ^\imath $
on a tensor product of a
![]() $U^\imath $
-module and a U-module from (5.3), we can now apply [Reference Bao, Wang and WatanabeBWW, (2.4)] and conclude that
$U^\imath $
-module and a U-module from (5.3), we can now apply [Reference Bao, Wang and WatanabeBWW, (2.4)] and conclude that
![]() $\psi ^\imath \left ({\widetilde {M}}_f\right )$
lies in the
$\psi ^\imath \left ({\widetilde {M}}_f\right )$
lies in the
![]() ${\mathbb Z}[q,q^{-1}]$
-space of the
${\mathbb Z}[q,q^{-1}]$
-space of the
![]() ${\widetilde {M}}_g$
s. This gives Part (2).
${\widetilde {M}}_g$
s. This gives Part (2).
Part (3) now follows from Part (2).
Now we can apply [Reference LusztigLu3, Lemma 24.2.1] and obtain the following.
Proposition 22. The
![]() $\mathbb {Q}(q)$
-vector space
$\mathbb {Q}(q)$
-vector space
![]() $\widehat {\mathbb T}^{m|n}_\zeta $
has unique
$\widehat {\mathbb T}^{m|n}_\zeta $
has unique
![]() $\psi ^\imath $
-invariant topological bases of the form
$\psi ^\imath $
-invariant topological bases of the form
such that
 $$ \begin{align*} \mathcal T^{\prime}_f=\widetilde{M}_f+\sum_{g\prec f}\texttt{t}^{\prime}_{gf}(q)\widetilde{M}_g, \quad \mathcal T_f={N}_f+\sum_{g\prec f}\texttt{t}_{gf}(q){N}_g, \quad {\mathcal{L}}_f=\widetilde{N}_f+\sum_{g\prec f}\texttt{l}_{gf}(q)\widetilde{N}_g, \end{align*} $$
$$ \begin{align*} \mathcal T^{\prime}_f=\widetilde{M}_f+\sum_{g\prec f}\texttt{t}^{\prime}_{gf}(q)\widetilde{M}_g, \quad \mathcal T_f={N}_f+\sum_{g\prec f}\texttt{t}_{gf}(q){N}_g, \quad {\mathcal{L}}_f=\widetilde{N}_f+\sum_{g\prec f}\texttt{l}_{gf}(q)\widetilde{N}_g, \end{align*} $$
with
![]() $\texttt {t}^{\prime }_{gf}(q),\texttt {t}_{gf}{(q)}\in q{\mathbb Z}[q]$
, and
$\texttt {t}^{\prime }_{gf}(q),\texttt {t}_{gf}{(q)}\in q{\mathbb Z}[q]$
, and
![]() $\texttt {l}_{gf}(q)\in q^{-1}{\mathbb Z}[q^{-1}]$
, for
$\texttt {l}_{gf}(q)\in q^{-1}{\mathbb Z}[q^{-1}]$
, for
![]() $g\prec f$
in
$g\prec f$
in
![]() ${\mathbb Z}^{m|n}_{\zeta -}$
.
${\mathbb Z}^{m|n}_{\zeta -}$
.
As usual, we adopt the convention
![]() $\texttt {t}^{\prime }_{ff}(q)=\texttt {t}_{ff}(q)=\texttt {l}_{ff}(q)=1$
,
$\texttt {t}^{\prime }_{ff}(q)=\texttt {t}_{ff}(q)=\texttt {l}_{ff}(q)=1$
,
![]() $\texttt {t}^{\prime }_{gf}=\texttt {t}_{gf}=\texttt {l}_{gf}=0$
for
$\texttt {t}^{\prime }_{gf}=\texttt {t}_{gf}=\texttt {l}_{gf}=0$
for
![]() $g\npreceq f$
.
$g\npreceq f$
.
5.5.
 $\imath $
-Canonical Bases on q-symmetric tensors
$\imath $
-Canonical Bases on q-symmetric tensors
This section compares the bases
![]() $\{T_f\}$
and
$\{T_f\}$
and
![]() $\{L_f\}$
with the bases
$\{L_f\}$
with the bases
![]() $\{\mathcal T_f\}$
and
$\{\mathcal T_f\}$
and
![]() $\{{\mathcal {L}}_f\}$
. Since this part is analogous to [Reference Chen, Coulembier and MazorchukCCM1, Section 3.7] and follows along the same line of arguments, we shall be brief and only summarize the main results.
$\{{\mathcal {L}}_f\}$
. Since this part is analogous to [Reference Chen, Coulembier and MazorchukCCM1, Section 3.7] and follows along the same line of arguments, we shall be brief and only summarize the main results.
Proposition 23. Let
![]() $f,g\in \mathbb {I}^{m|n}_{\zeta -}$
and
$f,g\in \mathbb {I}^{m|n}_{\zeta -}$
and
![]() $w_0^\zeta $
be the longest element in
$w_0^\zeta $
be the longest element in
![]() $W_\zeta $
. We have
$W_\zeta $
. We have
In particular, we have
![]() $\texttt {t}_{gf}=\texttt {t}^{\prime }_{gf} =t_{g\cdot w_0^\zeta ,f\cdot w_0^\zeta }$
and
$\texttt {t}_{gf}=\texttt {t}^{\prime }_{gf} =t_{g\cdot w_0^\zeta ,f\cdot w_0^\zeta }$
and
![]() $\texttt {l}_{gf} = \sum _{x\in W^g}\ell _{g\cdot x,f}q^{-\ell (x)}$
, where
$\texttt {l}_{gf} = \sum _{x\in W^g}\ell _{g\cdot x,f}q^{-\ell (x)}$
, where
![]() $W^g$
is the set of shortest length representatives
$W^g$
is the set of shortest length representatives
![]() $W_f\cap W_\zeta \backslash W_\zeta $
.
$W_f\cap W_\zeta \backslash W_\zeta $
.
Let
![]() $\phi _\zeta :\widehat {\mathbb T}^{m|n}\rightarrow \widehat {\mathbb T}^{m|n}_\zeta $
be the
$\phi _\zeta :\widehat {\mathbb T}^{m|n}\rightarrow \widehat {\mathbb T}^{m|n}_\zeta $
be the
![]() $U^\imath $
-module homomorphism defined by
$U^\imath $
-module homomorphism defined by
We have the following.
Theorem 24. Let
![]() $\phi _\zeta :\widehat {\mathbb T}^{m|n}\rightarrow \widehat {\mathbb T}^{m|n}_\zeta $
be the map in (5.9). For
$\phi _\zeta :\widehat {\mathbb T}^{m|n}\rightarrow \widehat {\mathbb T}^{m|n}_\zeta $
be the map in (5.9). For
![]() $f\in \mathbb {I}^{m|n}$
, let
$f\in \mathbb {I}^{m|n}$
, let
![]() $\tau $
be the minimum length element in
$\tau $
be the minimum length element in
![]() $W_\zeta $
such that
$W_\zeta $
such that
![]() $f\cdot \tau \in \mathbb {I}^{m|n}_{\zeta -}$
. Then we have
$f\cdot \tau \in \mathbb {I}^{m|n}_{\zeta -}$
. Then we have
-
(1)
 $\phi _\zeta \left ( M_f\right )=q^{-\ell (\tau )}\widetilde {N}_{f\cdot \tau }$
and
$\phi _\zeta \left ( M_f\right )=q^{-\ell (\tau )}\widetilde {N}_{f\cdot \tau }$
and
 $\phi _\zeta (\widetilde {M}_f)=q^{-\ell (\tau )}N_f$
.
$\phi _\zeta (\widetilde {M}_f)=q^{-\ell (\tau )}N_f$
. -
(2)
 $\phi _\zeta (T_{f\cdot w_0^\zeta })=\mathcal T_f$
, for
$\phi _\zeta (T_{f\cdot w_0^\zeta })=\mathcal T_f$
, for
 $f\in \mathbb {I}^{m|n}_{\zeta -}$
.
$f\in \mathbb {I}^{m|n}_{\zeta -}$
. -
(3)
 $\phi _\zeta \left (L_f\right )=\begin {cases} {\mathcal {L}}_f,&\text { if } f\in \mathbb {I}^{m|n}_{\zeta -},\\ 0,&\text { otherwise.} \end {cases}$
$\phi _\zeta \left (L_f\right )=\begin {cases} {\mathcal {L}}_f,&\text { if } f\in \mathbb {I}^{m|n}_{\zeta -},\\ 0,&\text { otherwise.} \end {cases}$
5.6. The quantum symmetric pair
 $(U,U^\jmath )$
and
$(U,U^\jmath )$
and
 $\jmath $
-canonical bases
$\jmath $
-canonical bases
A different coideal subalgebra
![]() $U^\jmath \subseteq U$
is introduced in [Reference Bao and WangBW, Chapter 6.1]. The pair
$U^\jmath \subseteq U$
is introduced in [Reference Bao and WangBW, Chapter 6.1]. The pair
![]() $(U,U^\jmath )$
forms a (different) quasi-split quantum symmetric pair of type AIII. A parallel theory of canonical and dual canonical bases, called
$(U,U^\jmath )$
forms a (different) quasi-split quantum symmetric pair of type AIII. A parallel theory of canonical and dual canonical bases, called
![]() $\jmath $
-canonical basis theory in loc. cit., based on a corresponding anti-linear involution on
$\jmath $
-canonical basis theory in loc. cit., based on a corresponding anti-linear involution on
![]() $U^\jmath $
is then developed. In particular, it follows that on a similar Fock space, which we denote by
$U^\jmath $
is then developed. In particular, it follows that on a similar Fock space, which we denote by
![]() $^\jmath \widehat {\mathbb {T}}^{m|n}$
, one has
$^\jmath \widehat {\mathbb {T}}^{m|n}$
, one has
![]() $\jmath $
-canonical and dual
$\jmath $
-canonical and dual
![]() $\jmath $
-canonical basis. Here, a difference is that in this new Fock space, the standard bases in both
$\jmath $
-canonical basis. Here, a difference is that in this new Fock space, the standard bases in both
![]() $\mathbb {V}$
and
$\mathbb {V}$
and
![]() $\mathbb {W}$
are now indexed by integers rather than half-integers so that set of the standard monomial basis is now in one-to-one correspondence with
$\mathbb {W}$
are now indexed by integers rather than half-integers so that set of the standard monomial basis is now in one-to-one correspondence with
![]() $^\jmath \mathbb {I}_{m|n}$
, the set of integer-valued functions of
$^\jmath \mathbb {I}_{m|n}$
, the set of integer-valued functions of
![]() $\{1,\cdots ,m;\bar {1},\cdots ,\bar {n}\}$
. In [Reference Bao and WangBW, Chapter 6.7], a version of
$\{1,\cdots ,m;\bar {1},\cdots ,\bar {n}\}$
. In [Reference Bao and WangBW, Chapter 6.7], a version of
![]() $(U^\jmath ,\mathcal H_{B_m})$
-duality on
$(U^\jmath ,\mathcal H_{B_m})$
-duality on
![]() $\mathbb {V}^{\otimes m}$
was established, which then allows us to obtain a corresponding analogue of Proposition 19 in this setting. This, in turn, enables us to construct the corresponding q-symmetrized Fock space, denoted by
$\mathbb {V}^{\otimes m}$
was established, which then allows us to obtain a corresponding analogue of Proposition 19 in this setting. This, in turn, enables us to construct the corresponding q-symmetrized Fock space, denoted by
![]() $^\jmath \mathbb {T}^{m|n}_\zeta $
, for
$^\jmath \mathbb {T}^{m|n}_\zeta $
, for
![]() $\zeta \in \mathrm {ch}\mathfrak {n}_{\bar 0}^+$
, and its completion
$\zeta \in \mathrm {ch}\mathfrak {n}_{\bar 0}^+$
, and its completion
![]() $^\jmath \widehat {\mathbb {T}}^{m|n}_\zeta $
, which gives rise to a canonical
$^\jmath \widehat {\mathbb {T}}^{m|n}_\zeta $
, which gives rise to a canonical
![]() $U^\jmath $
-epimorphism
$U^\jmath $
-epimorphism
![]() ${^\jmath }\phi _\zeta :{^\jmath }\widehat {\mathbb T}^{m|n}\rightarrow {^\jmath }\widehat {\mathbb T}^{m|n}_\zeta $
. A counterpart of the intertwiner for
${^\jmath }\phi _\zeta :{^\jmath }\widehat {\mathbb T}^{m|n}\rightarrow {^\jmath }\widehat {\mathbb T}^{m|n}_\zeta $
. A counterpart of the intertwiner for
![]() $(U,U^\jmath )$
is given [Reference Bao and WangBW, Chapter 6.2] with its integral property established in [Reference Bao and WangBW, Chapter 6.5]. This now provides us with all the necessary ingredients to repeat the constructions in Sections 5.1–5.5 for the quantum symmetric pair
$(U,U^\jmath )$
is given [Reference Bao and WangBW, Chapter 6.2] with its integral property established in [Reference Bao and WangBW, Chapter 6.5]. This now provides us with all the necessary ingredients to repeat the constructions in Sections 5.1–5.5 for the quantum symmetric pair
![]() $(U,U^\jmath )$
, leading to the construction of
$(U,U^\jmath )$
, leading to the construction of
![]() $\jmath $
-canonical and dual
$\jmath $
-canonical and dual
![]() $\jmath $
-canonical bases on q-symmetrized Fock space
$\jmath $
-canonical bases on q-symmetrized Fock space
![]() $^\jmath \widehat {\mathbb {T}}^{m|n}_\zeta $
and then finally to a counterpart of Theorem 24 in this setting.
$^\jmath \widehat {\mathbb {T}}^{m|n}_\zeta $
and then finally to a counterpart of Theorem 24 in this setting.
6. Category
 ${\mathcal {O}}$
for ortho-symplectic Lie superalgebras
${\mathcal {O}}$
for ortho-symplectic Lie superalgebras
In this section, we let
![]() $\mathfrak {g}$
be an ortho-symplectic Lie superalgebra. We shall recall the solution of the irreducible character problem for the ortho-symplectic Lie superalgebras in
$\mathfrak {g}$
be an ortho-symplectic Lie superalgebra. We shall recall the solution of the irreducible character problem for the ortho-symplectic Lie superalgebras in
![]() ${\mathcal {O}}_{\mathbb Z}$
of [Reference Bao and WangBW, Reference BaoBao]. This will be used in the subsequent section.
${\mathcal {O}}_{\mathbb Z}$
of [Reference Bao and WangBW, Reference BaoBao]. This will be used in the subsequent section.
6.1. Lie superalgebra of type B
For
![]() $\mathfrak {g}=\mathfrak {osp}(2m+1|2n)$
, we shall consider the following set of simple roots
$\mathfrak {g}=\mathfrak {osp}(2m+1|2n)$
, we shall consider the following set of simple roots
![]() $\Pi =\{-\epsilon _1,\epsilon _1-\epsilon _2,\cdots ,\epsilon _{m-1}-\epsilon _m,\epsilon _m-\delta _1,\delta _1-\delta _2,\cdots , \delta _{n-1}-\delta _n\}$
so that we have the following Dynkin diagram:
$\Pi =\{-\epsilon _1,\epsilon _1-\epsilon _2,\cdots ,\epsilon _{m-1}-\epsilon _m,\epsilon _m-\delta _1,\delta _1-\delta _2,\cdots , \delta _{n-1}-\delta _n\}$
so that we have the following Dynkin diagram:
Let
![]() $\mathfrak {b}$
denote the corresponding Borel subalgebra with the set of positive roots
$\mathfrak {b}$
denote the corresponding Borel subalgebra with the set of positive roots
![]() $\Phi ^+$
consisting of
$\Phi ^+$
consisting of
The Weyl vector equals

For
![]() $\lambda \in \mathfrak {h}^*$
, we define a function
$\lambda \in \mathfrak {h}^*$
, we define a function
![]() $f_\lambda :\{1,\cdots ,m;\bar {1},\cdots ,\bar {n}\}\rightarrow {\mathbb {C}}$
by
$f_\lambda :\{1,\cdots ,m;\bar {1},\cdots ,\bar {n}\}\rightarrow {\mathbb {C}}$
by
 $$ \begin{align*} f_\lambda(i):=\begin{cases} (\lambda+\rho,\epsilon_i),\quad\text{ for }i= 1,\cdots,m,\\ (\lambda+\rho,\delta_i),\quad\text{ for }i=\bar{1},\cdots,\bar{n}. \end{cases} \end{align*} $$
$$ \begin{align*} f_\lambda(i):=\begin{cases} (\lambda+\rho,\epsilon_i),\quad\text{ for }i= 1,\cdots,m,\\ (\lambda+\rho,\delta_i),\quad\text{ for }i=\bar{1},\cdots,\bar{n}. \end{cases} \end{align*} $$
Recall that
![]() $\Lambda $
denotes the set of integral weights. Denote by
$\Lambda $
denotes the set of integral weights. Denote by
![]() $\succeq $
the Bruhat order on
$\succeq $
the Bruhat order on
![]() $\Lambda $
with respect to the simple system above. We have the following subsets in
$\Lambda $
with respect to the simple system above. We have the following subsets in
![]() $\Lambda $
:
$\Lambda $
:

Note that if
![]() $\lambda \in \Lambda $
, but
$\lambda \in \Lambda $
, but
![]() $\lambda \not \in \Lambda ^{\texttt {int}}\cup \Lambda ^{\texttt {hf}}$
, then
$\lambda \not \in \Lambda ^{\texttt {int}}\cup \Lambda ^{\texttt {hf}}$
, then
![]() $\lambda $
is a typical weight. The assignment
$\lambda $
is a typical weight. The assignment
![]() $f\rightarrow f_\lambda $
restricts to bijections
$f\rightarrow f_\lambda $
restricts to bijections
![]() $\Lambda ^{\texttt {int}}\rightarrow \mathbb {I}_{m|n}$
and
$\Lambda ^{\texttt {int}}\rightarrow \mathbb {I}_{m|n}$
and
![]() $\Lambda ^{\texttt {hf}}\rightarrow {^\jmath \mathbb {I}_{m|n}}$
.
$\Lambda ^{\texttt {hf}}\rightarrow {^\jmath \mathbb {I}_{m|n}}$
.
Recall that we let
![]() ${\mathcal {O}}$
denote the BGG category and
${\mathcal {O}}$
denote the BGG category and
![]() ${\mathcal {O}}_{\mathbb Z}$
be the integral BGG subcategory for
${\mathcal {O}}_{\mathbb Z}$
be the integral BGG subcategory for
![]() $\mathfrak {g}$
, respectively. We further let
$\mathfrak {g}$
, respectively. We further let
![]() ${\mathcal {O}}^{\texttt {int}}_{\mathbb Z}$
and
${\mathcal {O}}^{\texttt {int}}_{\mathbb Z}$
and
![]() ${\mathcal {O}}^{\texttt {hf}}_{\mathbb Z}$
denote the full subcategories of
${\mathcal {O}}^{\texttt {hf}}_{\mathbb Z}$
denote the full subcategories of
![]() ${\mathcal {O}}_{\mathbb Z}$
consisting of objects with weights lying in
${\mathcal {O}}_{\mathbb Z}$
consisting of objects with weights lying in
![]() $\Lambda ^{\texttt {int}}$
and
$\Lambda ^{\texttt {int}}$
and
![]() $\Lambda ^{\texttt {hf}}$
, respectively. For
$\Lambda ^{\texttt {hf}}$
, respectively. For
![]() $\lambda \in \mathfrak {h}^*$
,
$\lambda \in \mathfrak {h}^*$
,
![]() $M(\lambda )$
denotes the Verma module of
$M(\lambda )$
denotes the Verma module of
![]() $\mathfrak {b}$
-highest weight
$\mathfrak {b}$
-highest weight
![]() $\lambda $
and
$\lambda $
and
![]() $L(\lambda )$
denotes its unique irreducible quotient. We also recall that
$L(\lambda )$
denotes its unique irreducible quotient. We also recall that
![]() $T^{{\mathcal {O}}}(\lambda )$
denotes the tilting module of highest
$T^{{\mathcal {O}}}(\lambda )$
denotes the tilting module of highest
![]() $\lambda $
in
$\lambda $
in
![]() ${\mathcal {O}}$
.
${\mathcal {O}}$
.
Let
![]() $K({\mathcal {O}})$
denote the Grothendieck group of
$K({\mathcal {O}})$
denote the Grothendieck group of
![]() ${\mathcal {O}}$
and
${\mathcal {O}}$
and
![]() $K({\mathcal {O}})_{\mathbb {Q}}=K({\mathcal {O}})\otimes _{\mathbb Z}\mathbb {Q}$
. The subgroup
$K({\mathcal {O}})_{\mathbb {Q}}=K({\mathcal {O}})\otimes _{\mathbb Z}\mathbb {Q}$
. The subgroup
![]() $K({\mathcal {O}}_{\mathbb Z})_{\mathbb {Q}}$
has basis
$K({\mathcal {O}}_{\mathbb Z})_{\mathbb {Q}}$
has basis
![]() $\{[M(\lambda )]\vert \lambda \in \Lambda \}$
. We have the self-explanatory notations of
$\{[M(\lambda )]\vert \lambda \in \Lambda \}$
. We have the self-explanatory notations of
![]() $K({\mathcal {O}}^{\texttt {int}}_{\mathbb Z})_{\mathbb {Q}}$
and
$K({\mathcal {O}}^{\texttt {int}}_{\mathbb Z})_{\mathbb {Q}}$
and
![]() $K({\mathcal {O}}^{\texttt {hf}}_{\mathbb Z})_{\mathbb {Q}}$
for the corresponding Grothendieck groups.
$K({\mathcal {O}}^{\texttt {hf}}_{\mathbb Z})_{\mathbb {Q}}$
for the corresponding Grothendieck groups.
We have a linear isomorphism
![]() $\psi :\mathbb {T}^{m|n}_{q=1}\rightarrow {K({\mathcal {O}}^{\texttt {int}}_{\mathbb Z})_{\mathbb {Q}}}$
at
$\psi :\mathbb {T}^{m|n}_{q=1}\rightarrow {K({\mathcal {O}}^{\texttt {int}}_{\mathbb Z})_{\mathbb {Q}}}$
at
![]() $q=1$
given by
$q=1$
given by
![]() $ M_{f_\lambda }\rightarrow [M(\lambda )]$
, by means of which we can define a topological completion
$ M_{f_\lambda }\rightarrow [M(\lambda )]$
, by means of which we can define a topological completion
![]() $\widehat {K}({\mathcal {O}}^{\texttt {int}}_{\mathbb Z})_{\mathbb {Q}}$
of
$\widehat {K}({\mathcal {O}}^{\texttt {int}}_{\mathbb Z})_{\mathbb {Q}}$
of
![]() ${K({\mathcal {O}}^{\texttt {int}}_{\mathbb Z})}_{\mathbb {Q}}$
. This gives a linear isomorphism
${K({\mathcal {O}}^{\texttt {int}}_{\mathbb Z})}_{\mathbb {Q}}$
. This gives a linear isomorphism
![]() $\psi : \widehat {\mathbb {T}}^{m|n}_{q=1}\rightarrow \widehat {K}({\mathcal {O}}^{\texttt {int}}_{\mathbb Z})_{\mathbb {Q}}$
at
$\psi : \widehat {\mathbb {T}}^{m|n}_{q=1}\rightarrow \widehat {K}({\mathcal {O}}^{\texttt {int}}_{\mathbb Z})_{\mathbb {Q}}$
at
![]() $q=1$
. Indeed,
$q=1$
. Indeed,
![]() $\psi $
is a
$\psi $
is a
![]() $U^\imath _{q=1}$
-homomorphism, where the action of the generators of
$U^\imath _{q=1}$
-homomorphism, where the action of the generators of
![]() $U^\imath _{q=1}$
on the Fock space correspond to that of certain translation functors (constructed by tensoring with symmetric powers of the natural module) acting on
$U^\imath _{q=1}$
on the Fock space correspond to that of certain translation functors (constructed by tensoring with symmetric powers of the natural module) acting on
![]() ${\mathcal {O}}^{\texttt {int}}_{\mathbb Z}$
[Reference Bao and WangBW, (11.3)–(11.5)]. We have the following solution of the irreducible character problem in
${\mathcal {O}}^{\texttt {int}}_{\mathbb Z}$
[Reference Bao and WangBW, (11.3)–(11.5)]. We have the following solution of the irreducible character problem in
![]() ${\mathcal {O}}^{\texttt {int}}_{\mathbb Z}$
.
${\mathcal {O}}^{\texttt {int}}_{\mathbb Z}$
.
Theorem 25. [Reference Bao and WangBW, Theorem 11.13] The map
![]() $\psi : \widehat {\mathbb {T}}^{m|n}_{q=1}\rightarrow \widehat {K}({\mathcal {O}}^{\texttt {int}}_{\mathbb Z})_{\mathbb {Q}}$
defined by sending
$\psi : \widehat {\mathbb {T}}^{m|n}_{q=1}\rightarrow \widehat {K}({\mathcal {O}}^{\texttt {int}}_{\mathbb Z})_{\mathbb {Q}}$
defined by sending
![]() $M_{f_\lambda }\rightarrow [M(\lambda )]$
satisfies
$M_{f_\lambda }\rightarrow [M(\lambda )]$
satisfies
In particular, we have
![]() $\mathrm {ch} L(\lambda )=\sum _{\mu \preceq \lambda }\ell _{f_\lambda ,f_\mu }(1)\mathrm {ch} M(\mu )$
.
$\mathrm {ch} L(\lambda )=\sum _{\mu \preceq \lambda }\ell _{f_\lambda ,f_\mu }(1)\mathrm {ch} M(\mu )$
.
Remark 26. For the category
![]() ${\mathcal {O}}^{\texttt {hf}}_{\mathbb Z}$
of half-integer weights of
${\mathcal {O}}^{\texttt {hf}}_{\mathbb Z}$
of half-integer weights of
![]() $\mathfrak {g}$
, we have a counterpart to Theorem 25 above, now with
$\mathfrak {g}$
, we have a counterpart to Theorem 25 above, now with
![]() $\widehat {\mathbb {T}}^{m|n}_{q=1}$
and
$\widehat {\mathbb {T}}^{m|n}_{q=1}$
and
![]() $\widehat {K}({\mathcal {O}}^{\texttt {int}}_{\mathbb Z})_{\mathbb {Q}}$
replaced by
$\widehat {K}({\mathcal {O}}^{\texttt {int}}_{\mathbb Z})_{\mathbb {Q}}$
replaced by
![]() $^\jmath \widehat {\mathbb {T}}^{m|n}_{q=1}$
and
$^\jmath \widehat {\mathbb {T}}^{m|n}_{q=1}$
and
![]() $\widehat {K}({\mathcal {O}}^{\texttt {hf}}_{\mathbb Z})_{\mathbb {Q}}$
, respectively [Reference Bao and WangBW, Theorem 12.5]. The linear isomorphism is indeed a
$\widehat {K}({\mathcal {O}}^{\texttt {hf}}_{\mathbb Z})_{\mathbb {Q}}$
, respectively [Reference Bao and WangBW, Theorem 12.5]. The linear isomorphism is indeed a
![]() $U^\jmath _{q=1}$
-homomorphism, where the action of the generators of
$U^\jmath _{q=1}$
-homomorphism, where the action of the generators of
![]() $U^\jmath _{q=1}$
corresponds to that of the same translation functors acting now on
$U^\jmath _{q=1}$
corresponds to that of the same translation functors acting now on
![]() ${\mathcal {O}}^{\texttt {hf}}_{\mathbb Z}$
[Reference Bao and WangBW, Remark 12.4]. The map again matches
${\mathcal {O}}^{\texttt {hf}}_{\mathbb Z}$
[Reference Bao and WangBW, Remark 12.4]. The map again matches
![]() $\jmath $
-canonical and dual
$\jmath $
-canonical and dual
![]() $\jmath $
-canonical basis elements of
$\jmath $
-canonical basis elements of
![]() $^\jmath \widehat {\mathbb {T}}^{m|n}_{q=1}$
with tilting and irreducible objects in
$^\jmath \widehat {\mathbb {T}}^{m|n}_{q=1}$
with tilting and irreducible objects in
![]() ${\mathcal {O}}^{\texttt {hf}}_{\mathbb Z}$
, respectively.
${\mathcal {O}}^{\texttt {hf}}_{\mathbb Z}$
, respectively.
6.2. Lie superalgebra of type D
There is a Kazhdan-Lusztig theory for the Lie superalgebra
![]() $\mathfrak {g}=\mathfrak {osp}(2m|2n)$
based on different
$\mathfrak {g}=\mathfrak {osp}(2m|2n)$
based on different
![]() $\imath $
-quantum groups. Indeed, similar Fock space realizations for the BGG categories of
$\imath $
-quantum groups. Indeed, similar Fock space realizations for the BGG categories of
![]() $\mathfrak {g}$
-modules of integer and half-integer weights were constructed in [Reference BaoBao]. In particular, an
$\mathfrak {g}$
-modules of integer and half-integer weights were constructed in [Reference BaoBao]. In particular, an
![]() $\mathfrak {osp}(2m|2n)$
-counterpart of Theorem 25 is obtained in[Reference BaoBao, Theorem 4.15] for both integer and half-integer weight modules in
$\mathfrak {osp}(2m|2n)$
-counterpart of Theorem 25 is obtained in[Reference BaoBao, Theorem 4.15] for both integer and half-integer weight modules in
![]() ${\mathcal {O}}_{\mathbb Z}$
.
${\mathcal {O}}_{\mathbb Z}$
.
7. Serre quotient functor and proof of Theorem 2
The Serre quotient functor
![]() $\pi : {{\mathcal {O}}_{\mathbb Z}}\rightarrow {\overline {{\mathcal {O}}}}$
satisfies the universal property as follows. If there is an exact functor
$\pi : {{\mathcal {O}}_{\mathbb Z}}\rightarrow {\overline {{\mathcal {O}}}}$
satisfies the universal property as follows. If there is an exact functor
![]() $F: {{\mathcal {O}}_{\mathbb Z}}\rightarrow \mathcal C$
, where
$F: {{\mathcal {O}}_{\mathbb Z}}\rightarrow \mathcal C$
, where
![]() $\mathcal C$
is an abelian category, such that
$\mathcal C$
is an abelian category, such that
![]() $F(X)=0$
for any
$F(X)=0$
for any
![]() $X\in \mathcal I_\zeta $
, then there is a unique exact functor
$X\in \mathcal I_\zeta $
, then there is a unique exact functor
![]() $F': {\overline {{\mathcal {O}}}}\rightarrow \mathcal C$
such that
$F': {\overline {{\mathcal {O}}}}\rightarrow \mathcal C$
such that
![]() $F=F'\circ \pi $
; see [Reference GabrielGa, Corollaries II.1.2 and III.1.3] for more details.
$F=F'\circ \pi $
; see [Reference GabrielGa, Corollaries II.1.2 and III.1.3] for more details.
In this section, we assume that
![]() $\mathfrak {g}$
is a basic Lie superalgebra; that is,
$\mathfrak {g}$
is a basic Lie superalgebra; that is,
![]() $\mathfrak {g}$
is one of the Lie superalgebras from (1.2) except for the series
$\mathfrak {g}$
is one of the Lie superalgebras from (1.2) except for the series
![]() $\mathfrak p(n)$
. We consider the restriction of the Backelin functor
$\mathfrak p(n)$
. We consider the restriction of the Backelin functor
![]() $\Gamma _\zeta $
to
$\Gamma _\zeta $
to
![]() ${\mathcal {O}}_{\mathbb Z}$
. We will prove that
${\mathcal {O}}_{\mathbb Z}$
. We will prove that
![]() $\Gamma _\zeta :{ {\mathcal {O}}_{\mathbb Z}\rightarrow \Gamma _\zeta ({\mathcal {O}}_{\mathbb Z})}$
also satisfies this universal property. As a consequence,
$\Gamma _\zeta :{ {\mathcal {O}}_{\mathbb Z}\rightarrow \Gamma _\zeta ({\mathcal {O}}_{\mathbb Z})}$
also satisfies this universal property. As a consequence,
![]() $\Gamma _\zeta $
provides an explicit realization of
$\Gamma _\zeta $
provides an explicit realization of
![]() $\pi $
, extending the results in [Reference Chen, Cheng and MazorchukCCM2, Corollary 37], where the cases of Lie superalgebras of type I, including
$\pi $
, extending the results in [Reference Chen, Cheng and MazorchukCCM2, Corollary 37], where the cases of Lie superalgebras of type I, including
![]() $\mathfrak p(n)$
, are considered. We shall now combine the results of the previous sections to complete the proof of Theorem 2.
$\mathfrak p(n)$
, are considered. We shall now combine the results of the previous sections to complete the proof of Theorem 2.
7.1. Functor
 $F_\zeta $
and Gorelik’s equivalence
$F_\zeta $
and Gorelik’s equivalence
Recall from [Reference ChenCh2, Theorem 26] (see also [Reference Chen, Cheng and MazorchukCCM2, Section 7.3]) that there is an exact functor from
![]() ${\mathcal {O}}_{\mathbb Z}$
to
${\mathcal {O}}_{\mathbb Z}$
to
![]() $\mathcal W(\zeta )$
:
$\mathcal W(\zeta )$
:
where
![]() $\nu \in \mathfrak {h}^\ast $
is a dominant and integral weight with the stabilizer subgroup
$\nu \in \mathfrak {h}^\ast $
is a dominant and integral weight with the stabilizer subgroup
![]() $W_\zeta $
. Here, for any
$W_\zeta $
. Here, for any
![]() $X\in {\mathcal {O}}$
, the
$X\in {\mathcal {O}}$
, the
![]() ${\mathcal {L}}(M_0(\nu ), X)$
denotes the maximal
${\mathcal {L}}(M_0(\nu ), X)$
denotes the maximal
![]() $(\mathfrak {g},\mathfrak {g}_{\bar 0})$
-submodule of
$(\mathfrak {g},\mathfrak {g}_{\bar 0})$
-submodule of
![]() $\operatorname {Hom}\nolimits _{\mathbb {C}}(M_0(\nu ),X)$
that is a direct sum of finite-dimensional
$\operatorname {Hom}\nolimits _{\mathbb {C}}(M_0(\nu ),X)$
that is a direct sum of finite-dimensional
![]() $\mathfrak {g}_{\bar 0}$
-modules with respect to the adjoint action of
$\mathfrak {g}_{\bar 0}$
-modules with respect to the adjoint action of
![]() $\mathfrak {g}_{\bar 0}$
.
$\mathfrak {g}_{\bar 0}$
.
The functor
![]() $F_\zeta (-)$
satisfies the universal property of the Serre quotient functor as described above and restricts to an equivalence between
$F_\zeta (-)$
satisfies the universal property of the Serre quotient functor as described above and restricts to an equivalence between
![]() ${\mathcal {O}}^{\zeta \text {-pres}}$
and
${\mathcal {O}}^{\zeta \text {-pres}}$
and
![]() $\mathcal W(\zeta )$
. In the case when
$\mathcal W(\zeta )$
. In the case when
![]() $\mathfrak {g}$
is of type I, the Backelin functor
$\mathfrak {g}$
is of type I, the Backelin functor
![]() $\Gamma _\zeta $
restricted to
$\Gamma _\zeta $
restricted to
![]() ${\mathcal {O}}_{\mathbb Z}$
and the functor
${\mathcal {O}}_{\mathbb Z}$
and the functor
![]() $F_\zeta $
are isomorphic; see [Reference Chen, Coulembier and MazorchukCCM1, Corollary 37].
$F_\zeta $
are isomorphic; see [Reference Chen, Coulembier and MazorchukCCM1, Corollary 37].
We put
![]() $\mathfrak {g}\operatorname {-mod}\nolimits _Z$
to be the category of all finitely generated
$\mathfrak {g}\operatorname {-mod}\nolimits _Z$
to be the category of all finitely generated
![]() $\mathfrak {g}$
-modules on which
$\mathfrak {g}$
-modules on which
![]() $Z(\mathfrak {g})$
acts locally finitely. For any central character
$Z(\mathfrak {g})$
acts locally finitely. For any central character
![]() $\chi $
of
$\chi $
of
![]() $\mathfrak {g}$
, we set
$\mathfrak {g}$
, we set
![]() $(\cdot )_\chi $
to be the endofunctor on
$(\cdot )_\chi $
to be the endofunctor on
![]() $\mathfrak {g}\operatorname {-mod}\nolimits _{Z}$
of taking the largest summand of modules annihilated by some power of the kernel
$\mathfrak {g}\operatorname {-mod}\nolimits _{Z}$
of taking the largest summand of modules annihilated by some power of the kernel
![]() $\ker (\chi )$
.
$\ker (\chi )$
.
Let
![]() $\chi $
be a strongly typical central character with a perfect mate
$\chi $
be a strongly typical central character with a perfect mate
![]() $\chi ^0$
in the sense of [Reference GorelikGo2]. Denote by
$\chi ^0$
in the sense of [Reference GorelikGo2]. Denote by
![]() ${\mathcal {O}}_{\chi }$
and
${\mathcal {O}}_{\chi }$
and
![]() ${\mathcal {O}}_{\chi ^0}$
the corresponding central blocks; namely,
${\mathcal {O}}_{\chi ^0}$
the corresponding central blocks; namely,
![]() ${\mathcal {O}}_{\chi }$
and
${\mathcal {O}}_{\chi }$
and
![]() ${\mathcal {O}}_{\chi ^0}$
are the full subcategories of objects in
${\mathcal {O}}_{\chi ^0}$
are the full subcategories of objects in
![]() ${\mathcal {O}}$
and
${\mathcal {O}}$
and
![]() ${\mathcal {O}}_{\bar 0}$
annihilated by some powers of
${\mathcal {O}}_{\bar 0}$
annihilated by some powers of
![]() $\ker (\chi )$
and
$\ker (\chi )$
and
![]() $\ker (\chi ^0)$
, respectively. The following lemma is due to Gorelik [Reference GorelikGo2] (see also [Reference CoulembierCo, Lemma 3.1]):
$\ker (\chi ^0)$
, respectively. The following lemma is due to Gorelik [Reference GorelikGo2] (see also [Reference CoulembierCo, Lemma 3.1]):
Lemma 27 (Gorelik).
Suppose that
![]() $\chi $
is a strongly typical central character with a perfect mate
$\chi $
is a strongly typical central character with a perfect mate
![]() $\chi ^0$
. The functors
$\chi ^0$
. The functors
give rise to a mutually inverse equivalence of central blocks
![]() ${\mathcal {O}}_{\chi }$
and
${\mathcal {O}}_{\chi }$
and
![]() ${\mathcal {O}}_{\chi ^0}$
. Furthermore, this equivalence of categories preserves Verma modules.
${\mathcal {O}}_{\chi ^0}$
. Furthermore, this equivalence of categories preserves Verma modules.
Lemma 28. Suppose that
![]() $\lambda , \lambda '\in \mathfrak {h}^\ast $
such that
$\lambda , \lambda '\in \mathfrak {h}^\ast $
such that
Then we have
Proof. First, we calculate
 $$ \begin{align*} &\operatorname{Res}\nolimits(M(\lambda,\zeta))_{\chi^0} \\ &= \operatorname{Res}\nolimits(\Gamma_\zeta(M(\lambda)))_{\chi^0} \text{ by } \text{Proposition } {4}\\ &=\Gamma_\zeta^0(\operatorname{Res}\nolimits(M(\lambda))_{\chi^0})\\ &=\Gamma_\zeta^0(M_0(\lambda'))\\ &=M_0(\lambda',\zeta) \text{ by } [{\text{Bac}}\ \text{Proposition 6.9}]. \end{align*} $$
$$ \begin{align*} &\operatorname{Res}\nolimits(M(\lambda,\zeta))_{\chi^0} \\ &= \operatorname{Res}\nolimits(\Gamma_\zeta(M(\lambda)))_{\chi^0} \text{ by } \text{Proposition } {4}\\ &=\Gamma_\zeta^0(\operatorname{Res}\nolimits(M(\lambda))_{\chi^0})\\ &=\Gamma_\zeta^0(M_0(\lambda'))\\ &=M_0(\lambda',\zeta) \text{ by } [{\text{Bac}}\ \text{Proposition 6.9}]. \end{align*} $$
Next, we calculate
 $$ \begin{align*} &\operatorname{Ind}\nolimits(M_0(\lambda',\zeta))_{\chi} \\ &= \operatorname{Ind}\nolimits(\Gamma_\zeta^0(M_0(\lambda')))_{\chi}\\ &=\Gamma_\zeta(\operatorname{Ind}\nolimits(M_0(\lambda')_{\chi})\\ &=\Gamma_\zeta(M(\lambda))\\ &=M(\lambda,\zeta) \text{ by } \text{Proposition } {4}. \end{align*} $$
$$ \begin{align*} &\operatorname{Ind}\nolimits(M_0(\lambda',\zeta))_{\chi} \\ &= \operatorname{Ind}\nolimits(\Gamma_\zeta^0(M_0(\lambda')))_{\chi}\\ &=\Gamma_\zeta(\operatorname{Ind}\nolimits(M_0(\lambda')_{\chi})\\ &=\Gamma_\zeta(M(\lambda))\\ &=M(\lambda,\zeta) \text{ by } \text{Proposition } {4}. \end{align*} $$
Finally, we calculate
 $$ \begin{align*} &F_\zeta(M(\lambda)) = F_\zeta(\operatorname{Ind}\nolimits(M_0(\lambda'))_{\chi})\\ &= \operatorname{Ind}\nolimits(F_\zeta^0(M_0(\lambda')))_\chi \\ &=\operatorname{Ind}\nolimits(M_0(\lambda',\zeta))_\chi \text{ by } [{\text{MSo}}, \text{Proposition } 5.15]. \\ &= M(\lambda,\zeta) \text{ by the isomorphism ({7.6}).}\\[-38pt] \end{align*} $$
$$ \begin{align*} &F_\zeta(M(\lambda)) = F_\zeta(\operatorname{Ind}\nolimits(M_0(\lambda'))_{\chi})\\ &= \operatorname{Ind}\nolimits(F_\zeta^0(M_0(\lambda')))_\chi \\ &=\operatorname{Ind}\nolimits(M_0(\lambda',\zeta))_\chi \text{ by } [{\text{MSo}}, \text{Proposition } 5.15]. \\ &= M(\lambda,\zeta) \text{ by the isomorphism ({7.6}).}\\[-38pt] \end{align*} $$
Corollary 29. The functors
![]() $\Gamma _\zeta (-)$
and
$\Gamma _\zeta (-)$
and
![]() $F_\zeta (-)$
from
$F_\zeta (-)$
from
![]() ${\mathcal {O}}_{\mathbb Z}$
to
${\mathcal {O}}_{\mathbb Z}$
to
![]() $\mathcal N(\zeta )$
are isomorphic. In particular, the Backelin functor
$\mathcal N(\zeta )$
are isomorphic. In particular, the Backelin functor
![]() $\Gamma _\zeta (-): { {\mathcal {O}}_{\mathbb Z}\rightarrow \mathcal W(\zeta )}$
satisfies the universal property of Serre quotient.
$\Gamma _\zeta (-): { {\mathcal {O}}_{\mathbb Z}\rightarrow \mathcal W(\zeta )}$
satisfies the universal property of Serre quotient.
Proof. Let
![]() $\lambda \in \mathfrak {h}^\ast $
be a strongly typical, dominant, integral and regular weight. Let
$\lambda \in \mathfrak {h}^\ast $
be a strongly typical, dominant, integral and regular weight. Let
![]() $\lambda '\in \mathfrak {h}^\ast $
be such that the central character
$\lambda '\in \mathfrak {h}^\ast $
be such that the central character
![]() $\chi ^0:=\chi ^0_{\lambda '}$
of
$\chi ^0:=\chi ^0_{\lambda '}$
of
![]() $\mathfrak {g}_{\bar 0}$
associated to
$\mathfrak {g}_{\bar 0}$
associated to
![]() $\lambda '$
is a perfect mate of
$\lambda '$
is a perfect mate of
![]() $\chi :=\chi _\lambda $
and
$\chi :=\chi _\lambda $
and
![]() $\operatorname {Res}\nolimits (M(\lambda ))_{\chi ^{0}} = M_0(\lambda ')$
. By Lemmas 27 and 28, it follows that
$\operatorname {Res}\nolimits (M(\lambda ))_{\chi ^{0}} = M_0(\lambda ')$
. By Lemmas 27 and 28, it follows that
Then we have
![]() $\Gamma _\zeta \cong F_\zeta $
by [Reference Chen, Cheng and MazorchukCCM2, Lemma 1] (see also [Reference Chen, Cheng and MazorchukCCM2, Corollary 37]). The conclusion follows.
$\Gamma _\zeta \cong F_\zeta $
by [Reference Chen, Cheng and MazorchukCCM2, Lemma 1] (see also [Reference Chen, Cheng and MazorchukCCM2, Corollary 37]). The conclusion follows.
Remark 30. Recall the coapproximation functor
![]() $\mathfrak j:{\mathcal {O}}_{\mathbb Z}\rightarrow {\mathcal {O}}^{{\zeta }\text {-pres}}$
from Section 4.1. By Lemma 28, under the equivalences of categories
$\mathfrak j:{\mathcal {O}}_{\mathbb Z}\rightarrow {\mathcal {O}}^{{\zeta }\text {-pres}}$
from Section 4.1. By Lemma 28, under the equivalences of categories
![]() ${\mathcal {O}}^{\zeta \text {-pres}}\cong \mathcal W(\zeta )\cong {\overline {{\mathcal {O}}}}$
, we have a correspondence between the simple objects
${\mathcal {O}}^{\zeta \text {-pres}}\cong \mathcal W(\zeta )\cong {\overline {{\mathcal {O}}}}$
, we have a correspondence between the simple objects
![]() $\mathfrak j(L(\lambda ))\cong P(\lambda )/Tr(\text {rad}P(\lambda ))$
,
$\mathfrak j(L(\lambda ))\cong P(\lambda )/Tr(\text {rad}P(\lambda ))$
,
![]() $L(\lambda ,\zeta )$
and
$L(\lambda ,\zeta )$
and
![]() $\pi (L(\lambda ))$
, and a correspondence between the proper standard objects
$\pi (L(\lambda ))$
, and a correspondence between the proper standard objects
![]() $\overline \Delta (\lambda )$
,
$\overline \Delta (\lambda )$
,
![]() $M(\lambda ,\zeta )$
and
$M(\lambda ,\zeta )$
and
![]() $\pi (M(\lambda ))$
. Here,
$\pi (M(\lambda ))$
. Here,
![]() $\text {rad}P(\lambda )$
denotes the radical of
$\text {rad}P(\lambda )$
denotes the radical of
![]() $P(\lambda )$
.
$P(\lambda )$
.
7.2. Proof of Theorem 2
In this section, we consider the case when
![]() $\mathfrak {g}$
is an ortho-symplectic Lie superalgebra and make connection between
$\mathfrak {g}$
is an ortho-symplectic Lie superalgebra and make connection between
![]() $\mathcal W(\zeta )$
and (dual)
$\mathcal W(\zeta )$
and (dual)
![]() $\imath $
-canonical bases on the q-symmetrized Fock space from Section 5.5.
$\imath $
-canonical bases on the q-symmetrized Fock space from Section 5.5.
First, suppose that
![]() $\mathfrak {g}=\mathfrak {osp}(2m+1|2n)$
. Let
$\mathfrak {g}=\mathfrak {osp}(2m+1|2n)$
. Let
![]() $\mathcal W(\zeta )^{\texttt {int}}$
be the full subcategory of
$\mathcal W(\zeta )^{\texttt {int}}$
be the full subcategory of
![]() $\mathcal W(\zeta )$
consisting of objects that have composition factors of the form
$\mathcal W(\zeta )$
consisting of objects that have composition factors of the form
![]() $L(\lambda ,\zeta )$
, with
$L(\lambda ,\zeta )$
, with
![]() $\lambda \in \Lambda ^{\texttt {int}}$
. Similarly, the full subcategory
$\lambda \in \Lambda ^{\texttt {int}}$
. Similarly, the full subcategory
![]() $\mathcal W(\zeta )^{\texttt {hf}}$
consists of objects that have composition factors of the form
$\mathcal W(\zeta )^{\texttt {hf}}$
consists of objects that have composition factors of the form
![]() $L(\lambda ,\zeta )$
, with
$L(\lambda ,\zeta )$
, with
![]() $\lambda \in \Lambda ^{\texttt {hf}}$
. We note that
$\lambda \in \Lambda ^{\texttt {hf}}$
. We note that
![]() $\Gamma _\zeta \left (P(\lambda )\right )$
,
$\Gamma _\zeta \left (P(\lambda )\right )$
,
![]() $\lambda \in {\Lambda (\zeta )}$
integral, are the projective indecomposable modules in
$\lambda \in {\Lambda (\zeta )}$
integral, are the projective indecomposable modules in
![]() $\mathcal W(\zeta )$
and there are no nontrivial extension between
$\mathcal W(\zeta )$
and there are no nontrivial extension between
![]() $L(\mu )$
and
$L(\mu )$
and
![]() $L(\nu )$
in
$L(\nu )$
in
![]() ${\mathcal {O}}_{\mathbb Z}$
with
${\mathcal {O}}_{\mathbb Z}$
with
![]() $\mu \in \Lambda ^{\texttt {int}}$
and
$\mu \in \Lambda ^{\texttt {int}}$
and
![]() $\nu \in \Lambda ^{\texttt {hf}}$
. It follows that there are no nontrivial extensions between modules from
$\nu \in \Lambda ^{\texttt {hf}}$
. It follows that there are no nontrivial extensions between modules from
![]() $\mathcal W(\zeta )^{\texttt {int}}$
and
$\mathcal W(\zeta )^{\texttt {int}}$
and
![]() $\mathcal W(\zeta )^{\texttt {hf}}$
, and indeed,
$\mathcal W(\zeta )^{\texttt {hf}}$
, and indeed,
![]() $\Gamma _\zeta ({\mathcal {O}}_{\mathbb Z}^{\texttt {int}})=\mathcal W(\zeta )^{\texttt {int}}$
and
$\Gamma _\zeta ({\mathcal {O}}_{\mathbb Z}^{\texttt {int}})=\mathcal W(\zeta )^{\texttt {int}}$
and
![]() $\Gamma _\zeta ({\mathcal {O}}_{\mathbb Z}^{\texttt {hf}})=\mathcal W(\zeta )^{\texttt {hf}}$
. Let
$\Gamma _\zeta ({\mathcal {O}}_{\mathbb Z}^{\texttt {hf}})=\mathcal W(\zeta )^{\texttt {hf}}$
. Let
![]() $K(\mathcal W(\zeta )^{\texttt {int}})_{\mathbb {Q}}$
and
$K(\mathcal W(\zeta )^{\texttt {int}})_{\mathbb {Q}}$
and
![]() $K(\mathcal W(\zeta )^{\texttt {hf}})_{\mathbb {Q}}$
denote the respective Grothendieck groups with rational coefficients.
$K(\mathcal W(\zeta )^{\texttt {hf}})_{\mathbb {Q}}$
denote the respective Grothendieck groups with rational coefficients.
Define the linear map
![]() $\psi _\zeta :\widehat {\mathbb {T}}^{m|n}_{\zeta ,q=1} \rightarrow \widehat {K}(\mathcal W(\zeta )^{\texttt {int}})_{\mathbb {Q}}$
at
$\psi _\zeta :\widehat {\mathbb {T}}^{m|n}_{\zeta ,q=1} \rightarrow \widehat {K}(\mathcal W(\zeta )^{\texttt {int}})_{\mathbb {Q}}$
at
![]() $q=1$
by
$q=1$
by
![]() $\psi _\zeta \left (\widetilde {N}_{f_\lambda }\right ):=[M(\lambda ,\zeta )]$
, for
$\psi _\zeta \left (\widetilde {N}_{f_\lambda }\right ):=[M(\lambda ,\zeta )]$
, for
![]() $\lambda \in {\Lambda (\zeta )}\cap \Lambda ^{\texttt {int}}$
. Here,
$\lambda \in {\Lambda (\zeta )}\cap \Lambda ^{\texttt {int}}$
. Here,
![]() $\widehat {K}(\mathcal W(\zeta )^{\texttt {int}})_{\mathbb {Q}}$
denotes the corresponding topological completion inherited from the topological completion of
$\widehat {K}(\mathcal W(\zeta )^{\texttt {int}})_{\mathbb {Q}}$
denotes the corresponding topological completion inherited from the topological completion of
![]() $\mathbb {T}^{m|n}_{\zeta ,q=1}$
via this map.
$\mathbb {T}^{m|n}_{\zeta ,q=1}$
via this map.
Theorem 31. Let
![]() $\mathfrak {g}=\mathfrak {osp}(2m+1|2n)$
.
$\mathfrak {g}=\mathfrak {osp}(2m+1|2n)$
.
-
(1) The functors
 $\Gamma _\zeta $
and
$\Gamma _\zeta $
and
 $F_\zeta $
from
$F_\zeta $
from
 ${\mathcal {O}}^{\texttt {int}}_{\mathbb {Z}}$
to
${\mathcal {O}}^{\texttt {int}}_{\mathbb {Z}}$
to
 $\mathcal W(\zeta )^{\texttt {int}}$
categorify the
$\mathcal W(\zeta )^{\texttt {int}}$
categorify the
 $U^\imath $
-homomorphism
$U^\imath $
-homomorphism
 $\phi _\zeta :\widehat {\mathbb {T}}^{m|n}_{q=1}\rightarrow \widehat {\mathbb {T}}^{m|n}_{\zeta ,q=1}$
at
$\phi _\zeta :\widehat {\mathbb {T}}^{m|n}_{q=1}\rightarrow \widehat {\mathbb {T}}^{m|n}_{\zeta ,q=1}$
at
 $q=1$
.
$q=1$
. -
(2) The map
 $\psi _\zeta $
sends
$\psi _\zeta $
sends
 $\imath $
-canonical and dual
$\imath $
-canonical and dual
 $\imath $
-canonical basis elements
$\imath $
-canonical basis elements
 ${\mathcal {L}}_{f_\lambda }$
and
${\mathcal {L}}_{f_\lambda }$
and
 $\mathcal T_{f_\lambda }$
to the tilting and simple objects corresponding to weight
$\mathcal T_{f_\lambda }$
to the tilting and simple objects corresponding to weight
 $\lambda \in \Lambda ^{{\texttt {int}}}{\cap {\Lambda (\zeta )}}$
, respectively.
$\lambda \in \Lambda ^{{\texttt {int}}}{\cap {\Lambda (\zeta )}}$
, respectively.
Proof. Let
![]() $\gamma _\zeta :K({\mathcal {O}}^{\texttt {int}}_{\mathbb {Z}})_{\mathbb {Q}}\rightarrow K(\mathcal W(\zeta ))_{\mathbb {Q}}$
be the map induced by the Backelin functor
$\gamma _\zeta :K({\mathcal {O}}^{\texttt {int}}_{\mathbb {Z}})_{\mathbb {Q}}\rightarrow K(\mathcal W(\zeta ))_{\mathbb {Q}}$
be the map induced by the Backelin functor
![]() $\Gamma _\zeta $
on the respective Grothendieck groups. It is evident that the image lies in
$\Gamma _\zeta $
on the respective Grothendieck groups. It is evident that the image lies in
![]() $K(\mathcal W(\zeta )^{\texttt {int}})_{\mathbb {Q}}$
. By Proposition 4 and Theorem 24 one verifies that
$K(\mathcal W(\zeta )^{\texttt {int}})_{\mathbb {Q}}$
. By Proposition 4 and Theorem 24 one verifies that
![]() $\gamma _\zeta \circ \psi $
and
$\gamma _\zeta \circ \psi $
and
![]() $\psi _\zeta \circ \phi _\zeta $
coincide on the monomial basis of
$\psi _\zeta \circ \phi _\zeta $
coincide on the monomial basis of
![]() $\mathbb {T}^{m|n}$
and hence
$\mathbb {T}^{m|n}$
and hence
![]() $\gamma _\zeta \circ \psi =\psi _\zeta \circ \phi _\zeta $
, which is precisely the commutativity of the diagram (1.6). We note that
$\gamma _\zeta \circ \psi =\psi _\zeta \circ \phi _\zeta $
, which is precisely the commutativity of the diagram (1.6). We note that
![]() $\phi _\zeta $
is a
$\phi _\zeta $
is a
![]() $U^\imath _{q=1}$
-homomorphism and the Backelin functor commutes with translation functors. Furthermore,
$U^\imath _{q=1}$
-homomorphism and the Backelin functor commutes with translation functors. Furthermore,
![]() $\psi $
is compatible with the
$\psi $
is compatible with the
![]() $U^\imath _{q=1}$
-action on
$U^\imath _{q=1}$
-action on
![]() $\widehat {\mathbb {T}}^{m|n}_{q=1}$
and certain
$\widehat {\mathbb {T}}^{m|n}_{q=1}$
and certain
![]() $\mathfrak {g}$
-translation functor action on
$\mathfrak {g}$
-translation functor action on
![]() ${\mathcal {O}}_{\mathbb Z}$
by [Reference Bao and WangBW, Proposition 11.9]. It follows therefore that the map
${\mathcal {O}}_{\mathbb Z}$
by [Reference Bao and WangBW, Proposition 11.9]. It follows therefore that the map
![]() $\psi _\zeta $
is also compatible with the
$\psi _\zeta $
is also compatible with the
![]() $U^\imath _{q=1}$
-action on
$U^\imath _{q=1}$
-action on
![]() $\widehat {\mathbb {T}}^{m|n}_\zeta $
and translation functor action on
$\widehat {\mathbb {T}}^{m|n}_\zeta $
and translation functor action on
![]() $\mathcal W(\zeta )^{\texttt {int}}$
.
$\mathcal W(\zeta )^{\texttt {int}}$
.
Part (1) is now a consequence of Proposition 4 and Theorem 6(ii), 24 and 25.
For
![]() $\lambda \in \Lambda (\zeta )\cap \Lambda ^{\texttt {int}}$
, we compute, using Theorems 6(ii), 24 and 25, that
$\lambda \in \Lambda (\zeta )\cap \Lambda ^{\texttt {int}}$
, we compute, using Theorems 6(ii), 24 and 25, that
This proves Part (2) for simple objects.
By Proposition 17, each tilting module in
![]() ${\mathcal {O}}^{{\zeta }\text {-pres}}$
is of the form
${\mathcal {O}}^{{\zeta }\text {-pres}}$
is of the form
![]() $T(\lambda )=T^{{\mathcal {O}}}(w_0^\zeta \cdot \lambda )\in {\mathcal {O}}^{\zeta \text {-pres}}$
for some
$T(\lambda )=T^{{\mathcal {O}}}(w_0^\zeta \cdot \lambda )\in {\mathcal {O}}^{\zeta \text {-pres}}$
for some
![]() $\lambda \in {\Lambda (\zeta )}$
. From this and the fact that the functors
$\lambda \in {\Lambda (\zeta )}$
. From this and the fact that the functors
![]() $\Gamma _\zeta $
and
$\Gamma _\zeta $
and
![]() $F_\zeta $
are isomorphic to the same Serre quotient functor, and
$F_\zeta $
are isomorphic to the same Serre quotient functor, and
![]() $F_\zeta $
restricts to an equivalence of categories from
$F_\zeta $
restricts to an equivalence of categories from
![]() ${\mathcal {O}}^{\zeta \text {-pres}}$
to
${\mathcal {O}}^{\zeta \text {-pres}}$
to
![]() $\mathcal W(\zeta )$
, it follows that
$\mathcal W(\zeta )$
, it follows that
![]() $\Gamma _\zeta (T^{{\mathcal {O}}}(w_0^\zeta \cdot \lambda ))$
is a tilting module in
$\Gamma _\zeta (T^{{\mathcal {O}}}(w_0^\zeta \cdot \lambda ))$
is a tilting module in
![]() $\mathcal W(\zeta )$
. By Theorem 24, for
$\mathcal W(\zeta )$
. By Theorem 24, for
![]() $\lambda \in {\Lambda (\zeta )}\cap \Lambda ^{\texttt {int}}$
, it follows that
$\lambda \in {\Lambda (\zeta )}\cap \Lambda ^{\texttt {int}}$
, it follows that
This completes the proof of Part (2).
We can formulate the following half-integer version of Theorem 31 with similar proof.
Theorem 32. Let
![]() $\mathfrak {g}=\mathfrak {osp}(2m+1|2n)$
.
$\mathfrak {g}=\mathfrak {osp}(2m+1|2n)$
.
-
(1) The functors
 $\Gamma _\zeta $
and
$\Gamma _\zeta $
and
 $F_\zeta $
from
$F_\zeta $
from
 ${\mathcal {O}}^{{\texttt {hf}}}_{\mathbb {Z}}$
to
${\mathcal {O}}^{{\texttt {hf}}}_{\mathbb {Z}}$
to
 $\mathcal W(\zeta )^{\texttt {hf}}$
categorify the
$\mathcal W(\zeta )^{\texttt {hf}}$
categorify the
 $U^\jmath $
-homomorphism
$U^\jmath $
-homomorphism
 ${^\jmath }\phi _\zeta :{^\jmath }\widehat {\mathbb {T}}^{m|n}_{q=1}\rightarrow {^\jmath }\widehat {\mathbb {T}}^{m|n}_{\zeta ,q=1}$
at
${^\jmath }\phi _\zeta :{^\jmath }\widehat {\mathbb {T}}^{m|n}_{q=1}\rightarrow {^\jmath }\widehat {\mathbb {T}}^{m|n}_{\zeta ,q=1}$
at
 $q=1$
.
$q=1$
. -
(2) The induced linear map
 ${^\jmath }\psi _\zeta :{^\jmath }\widehat {\mathbb {T}}^{m|n}_{\zeta ,q=1} \rightarrow \widehat {K}(\mathcal W(\zeta )^{\texttt {hf}})_{\mathbb {Q}}$
at
${^\jmath }\psi _\zeta :{^\jmath }\widehat {\mathbb {T}}^{m|n}_{\zeta ,q=1} \rightarrow \widehat {K}(\mathcal W(\zeta )^{\texttt {hf}})_{\mathbb {Q}}$
at
 $q=1$
that sends standard monomial basis elements to corresponding standard Whittaker module of weights in
$q=1$
that sends standard monomial basis elements to corresponding standard Whittaker module of weights in
 ${\Lambda (\zeta )}\cap \Lambda ^{\texttt {hf}}$
matches
${\Lambda (\zeta )}\cap \Lambda ^{\texttt {hf}}$
matches
 $\jmath $
-canonical and dual
$\jmath $
-canonical and dual
 $\jmath $
-canonical basis elements with the tilting and simple objects of weights in
$\jmath $
-canonical basis elements with the tilting and simple objects of weights in
 ${\Lambda (\zeta )}\cap \Lambda ^{{\texttt {hf}}}$
, respectively.
${\Lambda (\zeta )}\cap \Lambda ^{{\texttt {hf}}}$
, respectively.
Remark 33. As mentioned earlier in Section 6.2, we have Fock space realizations for the Kazhdan-Lusztig theory of type D Lie superalgebras in the integral category
![]() ${\mathcal {O}}$
[Reference BaoBao]. This allows us to obtain counterparts of Theorems 31 and 32 for the Lie superalgebra
${\mathcal {O}}$
[Reference BaoBao]. This allows us to obtain counterparts of Theorems 31 and 32 for the Lie superalgebra
![]() $\mathfrak {g}=\mathfrak {osp}(2m|2n)$
as well.
$\mathfrak {g}=\mathfrak {osp}(2m|2n)$
as well.
Remark 34. Theorem 31 states that the natural correspondence between certain standard monomial basis elements of
![]() $\widehat {\mathbb {T}}^{m|n}_\zeta $
and standard Whittaker modules identifies the
$\widehat {\mathbb {T}}^{m|n}_\zeta $
and standard Whittaker modules identifies the
![]() $\imath $
-canonical basis in
$\imath $
-canonical basis in
![]() $\widehat {\mathbb {T}}^{m|n}_\zeta $
with tilting objects in
$\widehat {\mathbb {T}}^{m|n}_\zeta $
with tilting objects in
![]() $\mathcal W(\zeta )$
. Indeed, using properties of
$\mathcal W(\zeta )$
. Indeed, using properties of
![]() $\psi ^\imath $
, we can construct a different bar involution on
$\psi ^\imath $
, we can construct a different bar involution on
![]() $\widehat {\mathbb {T}}^{m|n}$
and then on
$\widehat {\mathbb {T}}^{m|n}$
and then on
![]() $\widehat {\mathbb {T}}^{m|n}_\zeta $
compatible with the reverse Bruhat order (i.e., applying the bar involution to a standard monomial basis element gives a
$\widehat {\mathbb {T}}^{m|n}_\zeta $
compatible with the reverse Bruhat order (i.e., applying the bar involution to a standard monomial basis element gives a
![]() ${\mathbb Z}[q,q^{-1}]$
-linear combination of standard monomial basis elements corresponding to weights higher in the Bruhat ordering). Here, the completion is understood to be compatible with the reverse Bruhat ordering. In this setup, using Corollary 18, it can be shown that the natural correspondence between the standard monomial basis elements and standard Whittaker modules will now identify the dual
${\mathbb Z}[q,q^{-1}]$
-linear combination of standard monomial basis elements corresponding to weights higher in the Bruhat ordering). Here, the completion is understood to be compatible with the reverse Bruhat ordering. In this setup, using Corollary 18, it can be shown that the natural correspondence between the standard monomial basis elements and standard Whittaker modules will now identify the dual
![]() $\imath $
-canonical basis elements in
$\imath $
-canonical basis elements in
![]() $\widehat {\mathbb {T}}^{m|n}_\zeta $
with the projective indecomposable modules in
$\widehat {\mathbb {T}}^{m|n}_\zeta $
with the projective indecomposable modules in
![]() $\mathcal W(\zeta )$
. Similar version exists for
$\mathcal W(\zeta )$
. Similar version exists for
![]() $\jmath $
-canonical basis. We also have counterparts for
$\jmath $
-canonical basis. We also have counterparts for
![]() $\mathfrak {g}=\mathfrak {osp}(2m|2n)$
as well.
$\mathfrak {g}=\mathfrak {osp}(2m|2n)$
as well.
7.3. Annihilator ideals
For a given
![]() $\mathfrak g$
-module M, we denote by
$\mathfrak g$
-module M, we denote by
![]() ${\text {Ann}}_{\mathfrak {g}}M$
the annihilator ideal of M. The following corollary establishes an analogue of [Reference KostantKo, Theorem 3.9] for Lie algebras and [Reference ChenCh2, Theorem B] for Lie superalgebras of type I for basic Lie superalgebras:
${\text {Ann}}_{\mathfrak {g}}M$
the annihilator ideal of M. The following corollary establishes an analogue of [Reference KostantKo, Theorem 3.9] for Lie algebras and [Reference ChenCh2, Theorem B] for Lie superalgebras of type I for basic Lie superalgebras:
Corollary 35. We have
for any
![]() $\lambda \in {\Lambda (\zeta )}$
.
$\lambda \in {\Lambda (\zeta )}$
.
Proof. By [Reference ChenCh2, Theorem A(2), Theorem 26(2)], we have
for any
![]() $\lambda \in {\Lambda (\zeta )}$
. The corollary now follows from Theorem 6(ii) and Corollary 29.
$\lambda \in {\Lambda (\zeta )}$
. The corollary now follows from Theorem 6(ii) and Corollary 29.
Acknowledgments
We are grateful to Weiqiang Wang for alerting us to the relevance of [Reference Bao, Wang and WatanabeBWW] in Section 5.4. The authors are partially supported by National Science and Technology Council grants of the R.O.C., and they further acknowledge support from the National Center for Theoretical Sciences.
Competing interest
The authors have no competing interest to declare.
Financial support
The authors are partially supported by National Science and Technology Council grants of the R.O.C., and they further acknowledge support from the National Center for Theoretical Sciences.