Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T06:07:32.420Z Has data issue: false hasContentIssue false
  • English
  • Français

THE CASIMIR NUMBER AND THE DETERMINANT OF A FUSION CATEGORY

Part of: Hopf algebras, quantum groups and related topics Categories with structure

Published online by Cambridge University Press:  04 August 2020

ZHIHUA WANG ,
GONGXIANG LIU  and
LIBIN LI
ZHIHUA WANG
Affiliation:
Department of Mathematics, Taizhou University, Taizhou225300, China, e-mail: mailzhihua@126.com
GONGXIANG LIU
Affiliation:
Department of Mathematics, Nanjing University, Nanjing210093, China, e-mail: gxliu@nju.edu.cn
LIBIN LI
Affiliation:
School of Mathematical Science, Yangzhou University, Yangzhou225002, China, e-mail: lbli@yzu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 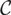$\mathcal{C}$ be a fusion category over an algebraically closed field 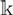$\mathbb{k}$ of arbitrary characteristic. Two numerical invariants of 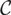$\mathcal{C}$ , that is, the Casimir number and the determinant of 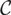$\mathcal{C}$ are considered in this paper. These two numbers are both positive integers and admit the property that the Grothendieck algebra 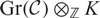$(\mathcal{C})\otimes_{\mathbb{Z}}K$ over any field K is semisimple if and only if any of these numbers is not zero in K. This shows that these two numbers have the same prime factors. If moreover 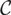$\mathcal{C}$ is pivotal, it gives a numerical criterion that 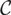$\mathcal{C}$ is nondegenerate if and only if any of these numbers is not zero in 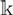$\mathbb{k}$ . For the case that 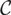$\mathcal{C}$ is a spherical fusion category over the field 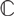$\mathbb{C}$ of complex numbers, these two numbers and the Frobenius–Schur exponent of 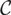$\mathcal{C}$ share the same prime factors. This may be thought of as another version of the Cauchy theorem for spherical fusion categories.

MSC classification

Primary: 18D10: Monoidal categories (= multiplicative categories), symmetric monoidal categories, braided categories
Secondary: 16T05: Hopf algebras and their applications
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 63 , Issue 2 , May 2021 , pp. 438 - 450
Copyright
© The Author(s), 2020. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bruillard, P., Ng, S. H., Rowell, E. and Wang, Z., Rank-finiteness for modular categories, J. Amer. Math. Soc. 29(3) (2016), 857–881.CrossRefGoogle Scholar
Caenepeel, S., Ion, B. and Militaru, G., The structure of Frobenius algebras and separable algebras, K-Theory 19(4) (2000), 365–402.CrossRefGoogle Scholar
Etingof, P. and Gelaki, S., On finite-dimensional semisimple and cosemisimple Hopf algebras in positive characteristic, Int. Math. Res. Not. IMRN 16 (1998), 851–864.CrossRefGoogle Scholar
Etingof, P., Gelaki, S., Nikshych, D. and Ostrik, V., Tensor Categories, Mathematical Surveys and Monographs, vol. 205 (Amer. Math. Soc., Providence, Rhode Island, 2015).Google Scholar
Etingof, P., Nikshych, D. and Ostrik, V., An analogue of Radford’s S 4 formula for finite tensor categories, Int. Math. Res. Not. IMRN 54 (2004), 2915–2933.CrossRefGoogle Scholar
Etingof, P., Nikshych, D. and Ostrik, V., On fusion categories, Ann. Math. 162 (2005), 581–642.CrossRefGoogle Scholar
Geck, M. and Pfeiffer, G., Characters of Finite Coxeter Groups and Iwahori-Hecke Algebras (Oxford University Press, New York, 2000).Google Scholar
Higman, D. G., On orders in separable algebras, Canad. J. Math. 7 (1955), 509–515.CrossRefGoogle Scholar
Lorenz, M., Some applications of Frobenius algebras to Hopf algebras, Contemp. Math. 537 (2011), 269–289.Google Scholar
Montgomery, S., Hopf Algebras and Their Actions on Rings , CBMS Series in Math, vol. 82 (Amer. Math. Soc., Providence, Rhode Island, 1993).Google Scholar
Müger, M., From subfactors to categories and topology. II. The quantum double of tensor categories and subfactors, J. Pure Appl. Algebra 180(1–2) (2003), 159–219.CrossRefGoogle Scholar
Ng, S. H. and Schauenburg, P., Frobenius-Schur indicators and exponents of spherical categories, Adv. Math. 211(1) (2007), 34–71.CrossRefGoogle Scholar
Nikshych, D., K 0-rings and twisting of finite dimensional semisimple Hopf algebras, Commun. Algebra 26(1) (1998), 321–342.CrossRefGoogle Scholar
Ostrik, V., On formal codegrees of fusion categories, Math. Res. Lett. 16(5) (2009), 895–901.CrossRefGoogle Scholar
Ostrik, V., On symmetric fusion categories in positive characteristic, arXiv:1503.01492, 2015.Google Scholar
Ostrik, V., Pivotal fusion categories of rank 3, Mosc. Math. J. 15(2) (2015), 373–396.CrossRefGoogle Scholar
Shimizu, K., The monoidal center and the character algebra, J. Pure Appl. Algebra 221(9) (2017), 2338–2371.CrossRefGoogle Scholar
Siehler, J., Near-group categories, Alg. Geom. Topol. 3(2) (2003), 719–775.CrossRefGoogle Scholar
Sommerhäuser, Y., On Kaplansky’s fifth conjecture, J. Algebra 204 (1998), 202–224.CrossRefGoogle Scholar
Wang, Z. and Li, L., On realization of fusion rings from generalized Cartan matrices. Acta Math. Sin. Engl. Ser. 33(3) (2017), 362–376.CrossRefGoogle Scholar
Wang, Z., Li, L. and Zhang, Y., A criterion for the Jacobson semisimplicity of the Green ring of a finite tensor category, Glasg. Math. J. 60(1) (2018), 253–272.CrossRefGoogle Scholar