No CrossRef data available.
Article contents
Galois representations of superelliptic curves
Published online by Cambridge University Press: 24 November 2022
Abstract
A superelliptic curve over a discrete valuation ring 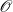 $\mathscr{O}$ of residual characteristic p is a curve given by an equation
$\mathscr{O}$ of residual characteristic p is a curve given by an equation 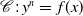 $\mathscr{C}\;:\; y^n=\,f(x)$, with
$\mathscr{C}\;:\; y^n=\,f(x)$, with 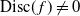 $\textrm{Disc}(\,f)\neq 0$. The purpose of this article is to describe the Galois representation attached to such a curve under the hypothesis that f(x) has all its roots in the fraction field of
$\textrm{Disc}(\,f)\neq 0$. The purpose of this article is to describe the Galois representation attached to such a curve under the hypothesis that f(x) has all its roots in the fraction field of 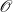 $\mathscr{O}$ and that
$\mathscr{O}$ and that 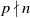 $p \nmid n$. Our results are inspired on the algorithm given in Bouw and WewersGlasg (Math. J. 59(1) (2017), 77–108.) but our description is given in terms of a cluster picture as defined in Dokchitser et al. (Algebraic curves and their applications, Contemporary Mathematics, vol. 724 (American Mathematical Society, Providence, RI, 2019), 73–135.).
$p \nmid n$. Our results are inspired on the algorithm given in Bouw and WewersGlasg (Math. J. 59(1) (2017), 77–108.) but our description is given in terms of a cluster picture as defined in Dokchitser et al. (Algebraic curves and their applications, Contemporary Mathematics, vol. 724 (American Mathematical Society, Providence, RI, 2019), 73–135.).
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust


