No CrossRef data available.
Article contents
On the Hilbert scheme of the moduli space of torsion-free sheaves on surfaces
Published online by Cambridge University Press: 02 February 2023
Abstract
The aim of this paper is to determine a bound of the dimension of an irreducible component of the Hilbert scheme of the moduli space of torsion-free sheaves on surfaces. Let X be a nonsingular irreducible complex surface, and let E be a vector bundle of rank n on X. We use the m-elementary transformation of E at a point 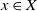 $x \in X$ to show that there exists an embedding from the Grassmannian variety
$x \in X$ to show that there exists an embedding from the Grassmannian variety 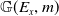 $\mathbb{G}(E_x,m)$ into the moduli space of torsion-free sheaves
$\mathbb{G}(E_x,m)$ into the moduli space of torsion-free sheaves 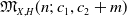 $\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)$ which induces an injective morphism from
$\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)$ which induces an injective morphism from 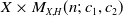 $X \times M_{X,H}(n;\,c_1,c_2)$ to
$X \times M_{X,H}(n;\,c_1,c_2)$ to 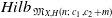 $Hilb_{\, \mathfrak{M}_{X,H}(n;\,c_1,c_2+m)}$.
$Hilb_{\, \mathfrak{M}_{X,H}(n;\,c_1,c_2+m)}$.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust



