Hostname: page-component-7dd5485656-pnlb5 Total loading time: 0.001 Render date: 2025-10-30T13:34:19.834Z Has data issue: false hasContentIssue false
  • English
  • Français

Stereographic compactification and affine bi-Lipschitz homeomorphisms

Part of: Metric geometry Model theory

Published online by Cambridge University Press:  16 May 2024

Vincent Grandjean  and
Roger Oliveira
Vincent Grandjean*
Affiliation:
Departamento de Matemática, Universidade Federal de Santa Catarina, Florianópolis, SC, 88.040-900, Brazil
Roger Oliveira
Affiliation:
Faculdade de Educação, Ciências e Letras do Sertão Central, Planalto Universitário, Quixadá, CE, 63900-000, Brazil
*
Corresponding author: Vincent Grandjean; Email: vincent.grandjean@ufsc.br
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 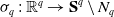$\sigma _q \,:\,{{\mathbb{R}}^q} \to{\textbf{S}}^q\setminus N_q$ be the inverse of the stereographic projection with center the north pole 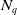$N_q$. Let 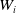$W_i$ be a closed subset of 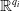${\mathbb{R}}^{q_i}$, for 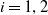$i=1,2$. Let 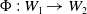$\Phi \,:\,W_1 \to W_2$ be a bi-Lipschitz homeomorphism. The main result states that the homeomorphism 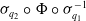$\sigma _{q_2}\circ \Phi \circ \sigma _{q_1}^{-1}$ is a bi-Lipschitz homeomorphism, extending bi-Lipschitz-ly at 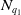$N_{q_1}$ with value 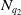$N_{q_2}$ whenever 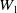$W_1$ is unbounded.

As two straightforward applications in the polynomially bounded o-minimal context over the real numbers, we obtain for free a version at infinity of: (1) Sampaio’s tangent cone result and (2) links preserving re-parametrization of definable bi-Lipschitz homeomorphisms of Valette.

Keywords

bi-Lipschitz homeomorphismEuclidean inversionStereographic compactification

MSC classification

Primary: 51F99: None of the above, but in this section
Secondary: 03C64: Model theory of ordered structures; o-minimality

Information

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 66 , Issue 3 , September 2024 , pp. 582 - 596
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Costa, A., Characterization of Lipschitz normally embedded complex curves and Lipschitz trivial values of polynomial mappings, PhD Thesis (Unversidade Federal do Ceará, 2023). Available at https://repositorio.ufc.br/handle/riufc/70235.CrossRefGoogle Scholar
Costa, A., Grandjean, V. and Michalska, M., Characterization of Lipschitz normally embedded complex curves, Bull. Sci. Math. 190 (2024), 103369. doi:10.1016/j.bulsci.2023.103369.CrossRefGoogle Scholar
Costa, A., Grandjean, V. and Michalska, M., One point compactification and Lipschitz normally embedded definable subsets, preprint 2023. https://arxiv.org/abs/2304.08555 Google Scholar
Costa, A., Grandjean, V. and Michalska, M., Global Lipschitz geometry of conic singular sub-manifolds with applications to algebraic sets, preprint 2023, https://arxiv.org/abs/2306.14854 Google Scholar
van den Dries, L., Tame topology and o-minimal structures, London Mathematical Society Lecture Note series, 1988, vol. 248 (Cambridge University Press).Google Scholar
Fernandes, A. and Sampaio, J. E., On Lipschitz rigidity of complex analytic sets, J. Geom. Anal. 30(1) (2020), 706–718. doi:10.1007/s12220-019-00162-x.CrossRefGoogle Scholar
Grandjean, V. and Oliveira, R., Stereographic compactification and affine bi-Lipschitz homeomorphisms, preprint available at https://arxiv.org/abs/2305.07469 Google Scholar
Heinonen, J., Lectures on Lipschitz Analysis, Lectures at the 14th Jyväskylä Summer School in August 2004.Google Scholar
Koike, S. and Paunescu, L., The directional dimension of subanalytic sets is invariant under bi-Lipschitz homeomorphisms, Ann. Inst. Fourier 59 (2009), 2448–2467.CrossRefGoogle Scholar
Oliveira, R., Equivalência assintótica forte e fraca de germes de funções semi-algébricas contínuas na origem e no infinito, PhD Thesis (Unversidade Federal do Ceará, 2022). Pdf available at https://repositorio.ufc.br/handle/riufc/68390 Google Scholar
Rademacher, H., Über partielle und totale differenzierbarkeit von funktionen mehrerer variabeln und über die transformation der doppelintegrale, Math. Ann. 79(4) (1919), 340–359.CrossRefGoogle Scholar
Sampaio, J. E., Bi-Lipschitz homeomorphic subanalytic sets have bi-Lipschitz homeomorphic tangent cones, Sel. Math. New Ser. 22(2) (2016), 553–559. doi:10.1007/s00029-015-0195-9.CrossRefGoogle Scholar
Sampaio, J. E., Local vs. global Lipschitz geometry, preprint 2023, Available at https://arxiv.org/abs/2305.11830 Google Scholar
Sampaio, J. E. and Silva, E. C., Bi-Lipschitz invariance and the uniqueness of tangent cones, J. Singularities 25 (2022), 393–402. doi:10.5427/jsing.2022.25s.CrossRefGoogle Scholar
Valette, G., Lipschitz triangulations, J. Math. 49(3) (2005), 953–979. doi:10.1215/ijm/1258138230.Google Scholar
Valette, G., The link of the germ of a semi-algebraic metric space, Proc. Am. Math. Soc. 135(10) (2007), 3083–3090.CrossRefGoogle Scholar
Valette, G., Poincaré duality for $L^p$ cohomology on subanalytic singular spaces, Math. Ann. 380(1-2) (2021), 789–823. doi:10.1007/s00208-021-02151-4.CrossRefGoogle Scholar
Valette, G., On Subanalytic Geometry, Book, in preparation. A preliminary version is available at http://www2.im.uj.edu.pl/gkw/sub.pdf.Google Scholar