Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T06:13:57.747Z Has data issue: false hasContentIssue false
  • English
  • Français

ACTIONS OF LIE SUPERALGEBRAS ON SEMIPRIME ALGEBRAS WITH CENTRAL INVARIANTS

Published online by Cambridge University Press:  24 June 2010

PIOTR GRZESZCZUK  and
MAŁGORZATA HRYNIEWICKA
PIOTR GRZESZCZUK
Affiliation:
Faculty of Computer Science, Bialystok University of Technology, Wiejska 45A, 15-351 Białystok, Poland e-mail: piotrgr@pb.edu.pl
MAŁGORZATA HRYNIEWICKA
Affiliation:
Institute of Mathematics, University of Białystok, Akademicka 2, 15-267 Białystok, Poland e-mail: margitt@math.uwb.edu.pl
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R be a semiprime algebra over a field 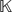of characteristic zero acted finitely on by a finite-dimensional Lie superalgebra L = L0 ⊕ L1. It is shown that if L is nilpotent, [L0, L1] = 0 and the subalgebra of invariants RL is central, then the action of L0 on R is trivial and R satisfies the standard polynomial identity of degree 2 ⋅ [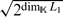]. Examples of actions of nilpotent Lie superalgebras, with central invariants and with [L0, L1] ≠ 0, are constructed.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 52 , Issue A: Rings and Modules in Honour of Patrick F. Smith's 65th Birthday , July 2010 , pp. 93 - 102
Copyright
Copyright © Glasgow Mathematical Journal Trust 2010

References

REFERENCES

1.Bergen, J. and Grzeszczuk, P., Invariants of Lie superalgebras acting on associative rings, Israel J. Math. 94 (1996), 403–428.CrossRefGoogle Scholar
2.Bergen, J. and Grzeszczuk, P., Invariants of Lie color algebras acting on graded algebras, Colloq. Math. 83 (2000), 107–124.CrossRefGoogle Scholar
3.Grzeszczuk, P. and Hryniewicka, M., Polynomial identities of algebras with actions of pointed Hopf algebras, J. Algebra 278 (2004), 684–703.CrossRefGoogle Scholar
4.Grzeszczuk, P. and Hryniewicka, M., Actions of pointed Hopf algebras with reduced invariants, Proc. Amer. Math. Soc. 135 (2007), 2381–2389.CrossRefGoogle Scholar
5.Jacobson, N., Structure of rings, vol. 37 (American Mathematical Society Colloquium Publications, Providence, RI, 1964).Google Scholar