Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-15T18:40:44.592Z Has data issue: false hasContentIssue false
  • English
  • Français

An algebraically closed field

Published online by Cambridge University Press:  18 May 2009

F. J. Rayner
F. J. Rayner
Affiliation:
University of Liverpool
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let k be any algebraically closed field, and denote by k((t)) the field of formal power series in one indeterminate t over k. Let

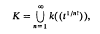
so that K is the field of Puiseux expansions with coefficients in k (each element of K is a formal power series in tl/r for some positive integer r). It is well-known that K is algebraically closed if and only if k is of characteristic zero [1, p. 61]. For examples relating to ramified extensions of fields with valuation [9, §6] it is useful to have a field analogous to K which is algebraically closed when k has non-zero characteristic p. In this paper, I prove that the set L of all formal power series of the form Σaitei (where (ei) is well-ordered, ei = mi|nprt, n ∈ Ζ, mi ∈ Ζ, ai ∈ k, ri ∈ Ν) forms an algebraically closed field.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 9 , Issue 2 , July 1968 , pp. 146 - 151
Copyright
Copyright © Glasgow Mathematical Journal Trust 1968

References

REFERENCES

1.Chevalley, C., Introduction to the theory of algebraic functions of one variable (New York, 1951).CrossRefGoogle Scholar
2.Hahn, H., Über die nichtarchimedischen Grossensysteme, S.-B. K. Akad. Wiss. Berlin. Kl. Math. 116 (IIa) (1907), 601–655.Google Scholar
3.Jacobson, N., Lectures in abstract algebra (Vol. III)—Theory of fields and Galois Theory (Princeton, 1964).Google Scholar
4.Krull, W., Allgemeine Bewertungstheorie, J. Reine Angew. Math. 167 (1932), 160–196.CrossRefGoogle Scholar
5.Moriya, M., Theorie der algebraischen Zahlkörper unendlichen Grades, J. Fac. Sci. Hokkaido Univ. 3 (1935), 107–190.Google Scholar
6.Neumann, B. H., On ordered division rings, Trans. Amer. Math. Soc. 66 (1949), 202–252.CrossRefGoogle Scholar
7.Ostrowski, A., Einige Fragen der allgemeine Körpertheorie, J. Reine Angew. Math. 143 (1913), 255–284.CrossRefGoogle Scholar
8.Rayner, F. J., Hensel's lemma, Quart. J. Math. Oxford Ser. (2) 8 (1957), 307–311.CrossRefGoogle Scholar
9.Rayner, F. J., Pseudo-convergent sequences in a field with a rank one valuation, Quart. J. Math. Oxford Ser. (2) 18 (1967), 315–324.CrossRefGoogle Scholar
10.Rayner, F. J., Relatively complete fields, Proc. Edinburgh Math. Soc. (2) 11 (1958), 131–133.CrossRefGoogle Scholar
11.Rim, Dock Sang, Relatively complete fields, Duke Math. J., 24 (1957), 197–200.CrossRefGoogle Scholar
12.Zariski, O. and Samuel, P., Commutative Algebra, Vol. II (Princeton, 1960).CrossRefGoogle Scholar