No CrossRef data available.
Published online by Cambridge University Press: 03 August 2022
Let
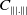 $C_{\||.\||}$
be an ideal of compact operators with symmetric norm
$C_{\||.\||}$
be an ideal of compact operators with symmetric norm
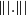 $\||.\||$
. In this paper, we extend the van Hemmen–Ando norm inequality for arbitrary bounded operators as follows: if f is an operator monotone function on
$\||.\||$
. In this paper, we extend the van Hemmen–Ando norm inequality for arbitrary bounded operators as follows: if f is an operator monotone function on
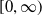 $[0,\infty)$
and S and T are bounded operators in
$[0,\infty)$
and S and T are bounded operators in
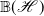 $\mathbb{B}(\mathscr{H}\;\,)$
such that
$\mathbb{B}(\mathscr{H}\;\,)$
such that
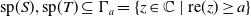 ${\rm{sp}}(S),{\rm{sp}}(T) \subseteq \Gamma_a=\{z\in \mathbb{C} \ | \ {\rm{re}}(z)\geq a\}$
, then
${\rm{sp}}(S),{\rm{sp}}(T) \subseteq \Gamma_a=\{z\in \mathbb{C} \ | \ {\rm{re}}(z)\geq a\}$
, then
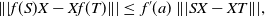 \begin{equation*}\||f(S)X-Xf(T)\|| \leq\;f'(a) \ \||SX-XT\||,\end{equation*}
\begin{equation*}\||f(S)X-Xf(T)\|| \leq\;f'(a) \ \||SX-XT\||,\end{equation*}
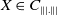 $X\in C_{\||.\||}$
. In particular, if
$X\in C_{\||.\||}$
. In particular, if
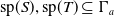 ${\rm{sp}}(S), {\rm{sp}}(T) \subseteq \Gamma_a$
, then
${\rm{sp}}(S), {\rm{sp}}(T) \subseteq \Gamma_a$
, then
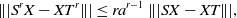 \begin{equation*}\||S^r X-XT^r\|| \leq r a^{r-1} \ \||SX-XT\||,\end{equation*}
\begin{equation*}\||S^r X-XT^r\|| \leq r a^{r-1} \ \||SX-XT\||,\end{equation*}
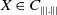 $X\in C_{\||.\||}$
and for each
$X\in C_{\||.\||}$
and for each
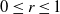 $0\leq r\leq 1$
.
$0\leq r\leq 1$
.