Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-15T13:25:18.245Z Has data issue: false hasContentIssue false
  • English
  • Français

An identity in combinatorial analysis

Published online by Cambridge University Press:  18 May 2009

L. J. Mordell
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a very recent paper [1], Basil Gordon discusses generalizations of Jacobi's identity

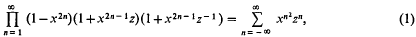
where x and z are complex numbers and |x| <1. He notes that some of its consequences, inter alia Euler's formula

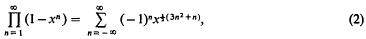
are of interest in number theory and combinatory analysis. He proves the apparently new and striking result

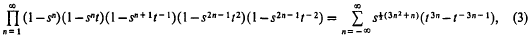
where |s|<1, and also considers the possibility of generalizations. His methods are algebraic and quite simple, but perhaps do not make obvious what underlies such formulae. It may be worth while to do so, especially since the details become simpler and the presentation more perspicuous. The method given here assumes no more knowledge than his does, although the new proof is expressed in terms of theta-functions, in simple properties of which, formulae such as (3) have their origin. Further, (3) appears in a slightly more symmetrical form.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 5 , Issue 4 , July 1962 , pp. 197 - 200
Copyright
Copyright © Glasgow Mathematical Journal Trust 1962

References

1.Gordon, Basil, Some identities in combinatorial analysis, Quart. J. Math. Oxford Ser. (2) 12 (1961), 285–290.CrossRefGoogle Scholar
2.Weber, H., Lehrbuch der Algebra (2nd edn, Braunschweig, 1908), Vol. III, p. 85.Google Scholar