Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Eastham, M. S. P.
1985.
The asymptotic solution of linear differential systems.
Mathematika,
Vol. 32,
Issue. 1,
p.
131.
Bartušek, Miroslav
and
Došlá, Zuzana
1997.
On the Limit‐Point /Limit‐Circle Problem for Nonlinear Third Order Differential Equations.
Mathematische Nachrichten,
Vol. 187,
Issue. 1,
p.
5.
Behncke, Horst
and
Hinton, Don
2005.
Deficiency indices and spectral theory of third order differential operators on the half line.
Mathematische Nachrichten,
Vol. 278,
Issue. 12-13,
p.
1430.

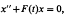
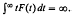 Several of these results have been unified by a theorem of F. V. Atkinson [
Several of these results have been unified by a theorem of F. V. Atkinson [

