No CrossRef data available.
Published online by Cambridge University Press: 20 April 2020
In 1996, a q-deformation of the universal enveloping algebra of the Schrödinger Lie algebra was introduced in Dobrev et al. [J. Phys. A 29 (1996) 5909–5918.]. This algebra is called the quantum Schrödinger algebra. In this paper, we study the Bernstein-Gelfand-Gelfand (BGG) category 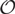 $\mathcal{O}$
for the quantum Schrödinger algebra
$\mathcal{O}$
for the quantum Schrödinger algebra 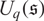 $U_q(\mathfrak{s})$
, where q is a nonzero complex number which is not a root of unity. If the central charge
$U_q(\mathfrak{s})$
, where q is a nonzero complex number which is not a root of unity. If the central charge 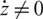 $\dot z\neq 0$
, using the module
$\dot z\neq 0$
, using the module 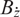 $B_{\dot z}$
over the quantum Weyl algebra
$B_{\dot z}$
over the quantum Weyl algebra 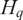 $H_q$
, we show that there is an equivalence between the full subcategory
$H_q$
, we show that there is an equivalence between the full subcategory 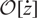 $\mathcal{O}[\dot Z]$
consisting of modules with the central charge
$\mathcal{O}[\dot Z]$
consisting of modules with the central charge 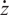 $\dot z$
and the BGG category
$\dot z$
and the BGG category 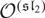 $\mathcal{O}^{(\mathfrak{sl}_2)}$
for the quantum group
$\mathcal{O}^{(\mathfrak{sl}_2)}$
for the quantum group 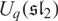 $U_q(\mathfrak{sl}_2)$
. In the case that
$U_q(\mathfrak{sl}_2)$
. In the case that 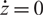 $\dot z = 0$
, we study the subcategory
$\dot z = 0$
, we study the subcategory 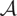 $\mathcal{A}$
consisting of finite dimensional
$\mathcal{A}$
consisting of finite dimensional 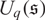 $U_q(\mathfrak{s})$
-modules of type 1 with zero action of Z. We directly construct an equivalence functor from
$U_q(\mathfrak{s})$
-modules of type 1 with zero action of Z. We directly construct an equivalence functor from 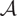 $\mathcal{A}$
to the category of finite dimensional representations of an infinite quiver with some quadratic relations. As a corollary, we show that the category of finite dimensional
$\mathcal{A}$
to the category of finite dimensional representations of an infinite quiver with some quadratic relations. As a corollary, we show that the category of finite dimensional 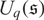 $U_q(\mathfrak{s})$
-modules is wild.
$U_q(\mathfrak{s})$
-modules is wild.