Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-16T03:39:16.544Z Has data issue: false hasContentIssue false
  • English
  • Français

Bilinear forms on vector Hardy spaces

Published online by Cambridge University Press:  18 May 2009

Gordon Blower
Gordon Blower
Affiliation:
Department of Mathematics and Statistics, Lancaster University, Lancaster Lai 4Yf, England, U.K.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let φ: 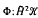ℋ → 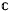be a bilinear form on vector Hardy space. Introduce the symbol φ of Φ by (φ (Z1, Z2), a ⊗ b) = Φ (K21 ⊗ a, K22 ⊗ b ), where Kw is the reproducing kernel for w ∈ D. We show that Φ extends to a bounded bilinear form on 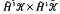provided that the gradient 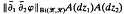defines a Carleson measure in the bidisc D2. We obtain a sufficient condition for Φ to extend to a Hilbert space. For vectorial bilinear Hankel forms we obtain an analogue of Nehari's Theorem.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 39 , Issue 3 , September 1997 , pp. 371 - 378
Copyright
Copyright © Glasgow Mathematical Journal Trust 1997

References

REFERENCES

1.Blower, G., Quadratic integrals and factorization of linear operators, J. London Math. Soc. (2), to appear.Google Scholar
2.Bourgain, J., New Banach space properties of the disc algebra and H ∞, Ada Math. 152 (1984), 1–48.Google Scholar
3.Bourgain, J., Vector-valued singular integrals and the H 1 – BMO duality, in Probability Theory and Harmonic Analysis, Editors Chao, J. A. and Woyczyński, W. A. (Marcel Dekker, New York, 1986), 1–19.Google Scholar
4.Chang, S-Y. A., Carleson measure on the bi-disc, Annals of Math. 109 (1979), 613–620.CrossRefGoogle Scholar
5.Fefferman, R., Bounded mean oscillation on the polydisk, Annals of Math. 110 (1979), 395–406.CrossRefGoogle Scholar
6.Koosis, P., Introduction to Hp spaces, London Mathematical Society Lecture Note Series 40 (Cambridge University Press, Cambridge 1980).Google Scholar
7.Merdy, C. Le, The Adamjan-Arov-Krein theorem on H p-spaces (2 ≤ p ≥ ∞) and on the disc algebra, Bull. London Math. Soc. 25 (1993), 275–281.CrossRefGoogle Scholar
8.Pisier, G., Factorization of linear operators and geometry of Banach spaces (AMS Regional Conference Series 60. AMS, Providence Rhode Island, 1986).CrossRefGoogle Scholar
9.Pisier, G., Factorization of operator valued analytic functions, Adv. Math. 93 (1992), 61–125.CrossRefGoogle Scholar
10.Power, S. C., Hankel operators on Hilbert space, Bull. London Math. Soc. 12 (1980), 422–442.CrossRefGoogle Scholar