Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lemmermeyer, F.
1997.
On 2-ciass field towers of some imaginary quadratic number fields.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 67,
Issue. 1,
p.
205.
Benjamin, Elliot
Lemmermeyer, Franz
and
Snyder, C.
1998.
Real Quadratic Fields with Abelian 2-Class Field Tower.
Journal of Number Theory,
Vol. 73,
Issue. 2,
p.
182.
Benjamin, Elliot
1999.
On the Second Hilbert 2-Class Field of Real Quadratic Number Fields with 2-Class Group Isomorphic to $(2,2^n)$, $n\ge2$.
Rocky Mountain Journal of Mathematics,
Vol. 29,
Issue. 3,
Benjamin, Elliot
and
Parry, Charles J.
1999.
Refined Lower Bounds on the 2-Class Number of the Hilbert 2-Class Field of Imaginary Quadratic Number Fields with Elementary 2-Class Group of Rank 3.
Journal of Number Theory,
Vol. 76,
Issue. 2,
p.
167.
Benjamin, Elliot
2006.
On the 2-class field tower of some imaginary biquadratic number fields.
The Ramanujan Journal,
Vol. 11,
Issue. 1,
p.
103.
Azizi, Abdelmalek
Zekhnini, Abdelkader
and
Taous, Mohammed
2014.
On the 2-class field tower of $$\mathbb Q (\sqrt{2p_1p_2},i)$$ Q ( 2 p 1 p 2 , i ) and the Galois group of its second Hilbert 2-class field.
Collectanea Mathematica,
Vol. 65,
Issue. 1,
p.
131.
Benjamin, Elliot
and
Snyder, C
2018.
On the rank of the 2-class group of the Hilbert 2-class field of some quadratic fields.
The Quarterly Journal of Mathematics,
González-Avilés, Cristian D.
2019.
Čech cohomology and the capitulation kernel.
Functiones et Approximatio Commentarii Mathematici,
Vol. 61,
Issue. 1,
Laxmi, H.
and
Saikia, Anupam
2024.
$$\mathbb {Z}_2$$-extension of real quadratic fields with $$\mathbb {Z}/2\mathbb {Z}$$ as 2-class group at each layer.
The Ramanujan Journal,
Vol. 64,
Issue. 4,
p.
1285.
Madrari, S. El
Taous, M.
and
Zekhnini, A.
2025.
Pólya groups and capitulation in some real biquadratic number fields.
Research in Number Theory,
Vol. 11,
Issue. 4,

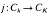
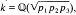 with distinct primes
with distinct primes 