Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
González, Manuel
and
Salas-Brown, Margot
2023.
Two classes of operators related to the perturbation classes problem.
Advances in Operator Theory,
Vol. 8,
Issue. 3,

 and it is contained in the perturbation class of the upper semi-Fredholm operators
and it is contained in the perturbation class of the upper semi-Fredholm operators 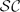 and the perturbation class of the lower semi-Fredholm operators
and the perturbation class of the lower semi-Fredholm operators 