Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T06:25:05.003Z Has data issue: false hasContentIssue false
  • English
  • Français

COCOMPACT LATTICES ON Ãn BUILDINGS

Part of: Finite geometry and special incidence structures Structure and classification of infinite or finite groups Linear algebraic groups and related topics

Published online by Cambridge University Press:  17 December 2014

INNA CAPDEBOSCQ ,
DMITRIY RUMYNIN  and
ANNE THOMAS
INNA CAPDEBOSCQ
Affiliation:
Mathematics Institute, Zeeman Building, University of Warwick, Coventry CV4 7AL, United Kingdom e-mail: I.Capdeboscq@warwick.ac.uk
DMITRIY RUMYNIN
Affiliation:
Mathematics Institute, Zeeman Building, University of Warwick, Coventry CV4 7AL, United Kingdom e-mail: D.Rumynin@warwick.ac.uk
ANNE THOMAS
Affiliation:
School of Mathematics and Statistics, University of Glasgow, 15 University Gardens, Glasgow G12 8QW, United Kingdom e-mail: anne.thomas@glasgow.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We construct cocompact lattices Γ'0 < Γ0 in the group G = PGLd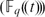$({\mathbb{F}_q(\!(t)\!)\!})$ which are type-preserving and act transitively on the set of vertices of each type in the building Δ associated to G. These lattices are commensurable with the lattices of Cartwright–Steger Isr. J. Math.103 (1998), 125–140. The stabiliser of each vertex in Γ'0 is a Singer cycle and the stabiliser of each vertex in Γ0 is isomorphic to the normaliser of a Singer cycle in PGLd(q). We show that the intersections of Γ'0 and Γ0 with PSLd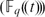$({\mathbb{F}_q(\!(t)\!)\!})$ are lattices in PSLd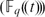$({\mathbb{F}_q(\!(t)\!)\!})$, and identify the pairs (d, q) such that the entire lattice Γ'0 or Γ0 is contained in PSLd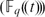$({\mathbb{F}_q(\!(t)\!)\!})$. Finally we discuss minimality of covolumes of cocompact lattices in SL3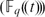$({\mathbb{F}_q(\!(t)\!)\!})$. Our proofs combine the construction of Cartwright–Steger Isr. J. Math.103 (1998), 125–140 with results about Singer cycles and their normalisers, and geometric arguments.

MSC classification

Primary: 20E42: Groups with a $BN$-pair; buildings
Secondary: 51E24: Buildings and the geometry of diagrams 20G44: Kac-Moody groups
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 57 , Issue 2 , May 2015 , pp. 241 - 262
Copyright
Copyright © Glasgow Mathematical Journal Trust 2014 

References

REFERENCES

1.Bass, H., Covering theory for graphs of groups J. Pure Appl. Algebra 89 (1993), 3–47.Google Scholar
2.Bass, H. and Lubotzky, A.. Tree lattices, in Progress in Mathematics, vol. 176 (Bass, H., Carbone, L., Lubotzky, A., Rosenberg, G. and Tits, J., Editors) (Birkhäuser Boston, Inc., Boston, MA, 2001), xiv+233.Google Scholar
3.Borel, A. and Harder, G., Existence of discrete cocompact subgroups of reductive groups over local fields J. Reine Angew. Math. 298 (1978), 53–64.Google Scholar
4.Borel, A. and Chandra, H., Arithmetic subgroups of algebraic groups Ann. Math. 75 (1962), 485–535.CrossRefGoogle Scholar
5.Bridson, M. R. and Haefliger, A., Metric spaces of non-positive curvature (Springer-Verlag, Berlin, 1999).CrossRefGoogle Scholar
6.Cartwright, D. I., Mantero, A. M., Steger, T. and Zappa, A., Groups acting simply transitively on the vertices of a building of type à 2 I, Geom. Dedicata 47 (1993), 143–166.Google Scholar
7.Cartwright, D. I. and Steger, T., A family of Ãn–groups Isr. J. Math. 103 (1998), 125–140.Google Scholar
8.Caprace, P.-E. and Rémy, B., Simplicity and superrigidity of twin building lattices, Invent. Math. 176 (2009), 169–221.CrossRefGoogle Scholar
9.Capdeboscq, I. K. and Thomas, A., Lattices in complete rank 2 Kac–Moody groups J. Pure Appl. Algebr. 216 (2011), 1348–1371.CrossRefGoogle Scholar
10.Cossidente, A. and De Resmini, M. J., Remarks on singer cyclic groups and their normalizers, Des. Codes Cryptogr. 32 (2004), 97–102.Google Scholar
11.Essert, J., A geometric construction of panel-regular lattices for buildings of type à 2 and 2 Algebr. Geom. Topol. 13 (2013), 1531–1578.CrossRefGoogle Scholar
12.Figá-Talamanca, A. and Nebbia, C., Harmonic analysis and representation theory for groups acting on homogeneous trees, London Mathematical Society Lecture Note Series, vol. 162 (Cambridge University Press, 1991).CrossRefGoogle Scholar
13.Gelfand, I. M., Graev, M. I. and Piatetsky-Shapiro, I., Representation theory and automorphic functions (Saunders, San Francisco, 1969).Google Scholar
14.Gorenstein, D., Lyons, R. and Solomon, R., The classification of finite simple groups, Number 3, Part I. Mathematical Surveys and Monographs, vol. 40 (American Mathematical Society, Providence, RI, 1998).Google Scholar
15.Jacobson, N., PI–algebras. An introduction, Lecture Notes in Mathematics, vol. 441 (Springer-Verlag, Berlin-New York, 1975).Google Scholar
16.Kantor, W. M., Liebler, R. A. and Tits, J., On discrete chamber-transitive automorphism groups of affine buildings, Bull. Am. Math. Soc. 16 (1987), 129–133.CrossRefGoogle Scholar
17.Kazhdan, D. A. and Margulis, G. A., A proof of Selberg's hypothesis, Mat. Sb. (N.S.) 75 (117) (1968), 163–168.Google Scholar
18.Lubotzky, A., Lattices of minimal covolume in SL 2: a nonarchimedean analogue of Siegel's theorem μ≥π/21 J. Am. Math. Soc. 3 (1990), 961–975.Google Scholar
19.Lubotzky, A., Lattices in rank one Lie groups over local fields Geom. Funct. Anal. 1 (1991), 406–431.CrossRefGoogle Scholar
20.Lubotzky, A. and Weigel, Th., Lattices of minimal covolume in SL 2 over local fields, Proc. London Math. Soc. 78 (1999), 283–333.Google Scholar
21.Margulis, G., Discrete subgroups of semisimple Lie froups, (Springer-Verlag, Berlin, 1991).Google Scholar
22.Mostow, G. D. and Tamagawa, T., On the cocompactness of arithmetically defined homogeneous spaces Ann. Math. 76 (1962), 446–463.Google Scholar
23.Pierce, R. S., Associative algebras, Graduate Texts in Mathematics, vol. 88. Studies in the History of Modern Science, 9. (Springer-Verlag, New York-Berlin, 1982).Google Scholar
24.Ronan, M. A., Triangle geometries, J. Comb. Theory Ser. A 37 (1984), 294–319.CrossRefGoogle Scholar
25.Ronan, M. A., Lectures on buildings, Perspectives in Mathematics, vol. 7. (Academic Press, Inc., Boston, MA, 1989).Google Scholar
26.Raghunathan, M. C., Discrete subgroups of algebraic groups over local fields of positive characteristics, Proceedings of the Indian Academy of Science (math. sci.) 99 (2) (1989), 127–146.Google Scholar
27.Salehi Golsefidy, A., Lattices of minimum covolume in Chevalley groups over local fields of positive characteristics, Duke Math. J. 146 (2) (2009), 227–251.Google Scholar
28.Tits, J., Buildings of spherical type and finite BN–pairs, Lecture Notes in Mathematics, vol. 386, (Springer-Verlag, New York, 1974).Google Scholar
29.Tits, J., Endliche Spielungsgruppen, die als Weylgruppen auftreten, Invent. Math. (1977), 283–295.Google Scholar
30.Tits, J., Immeubles de type affine, Buildings and the geometry of diagrams (Rosati, L. A., Editor) Lecture Notes in Mathematics, vol. 1181 (Springer-Verlag, Berlin, 1986) 159–190.CrossRefGoogle Scholar