Compactifications of totally bounded quasi-uniform spaces

Extract

The notation and terminology of this paper coincide with that of reference [4], except that here the term, compactification, refers to a T¹-space. It is known that a completely regular totally bounded Hausdorff quasi-uniform space (X, 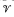) has a Hausdorff compactification if and only if 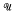contains a uniformity compatible with ℱ(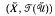) [4, Theorem 3.47]. The use of regular filters by E. M. Alfsen and J. E. Fenstad [1] and O. Njåstad [5], suggests a construction of a compactification, which differs markedly from the construction obtained in [4]. We use this construction to show that a totally bounded T₁ quasi-uniform space has a compactification if and only if it is point symmetric. While it is pleasant to have a characterization that obtains for all T₁-spaces, the present construction has several further attributes. Unlike the compactification obtained in [4], the compactification given here preserves both total boundedness and uniform weight, and coincides with the uniform completion when the quasi-uniformity under consideration is a uniformity. Moreover, any quasi-uniformly continuous map from the underlying quasi-uniform space of the compactification onto any totally bounded compact T₁-space has a quasi-uniformly continuous extension to the compactification. If is the Pervin quasi-uniformity of a T₁-space X, the compactification 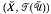we obtain is the Wallman compactification of (X, ℱ (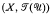)). It follows that our construction need not provide a Hausdorff compactification, even when such a compactification exists; but we obtain a sufficient condition in order that our compactification be a Hausdorff space and note that this condition is satisfied by all uniform spaces and all normal equinormal quasi-uniform spaces. Finally, we note that our construction is reminiscent of the completion obtained by Á. Császár for an arbitrary quasi-uniform space [2, Section 3]; in particular our Theorem 3.7 is comparable with the result of [2, Theorem 3.5].