Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-15T10:47:19.599Z Has data issue: false hasContentIssue false
  • English
  • Français

Compatible tight Riesz orders and prime subgroups

Published online by Cambridge University Press:  18 May 2009

N. R. Reilly
N. R. Reilly
Affiliation:
Simon Fraser University, Burnaby 2, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A tight Riesz group is a partially ordered group which satisfies a strengthened form of the Riesz interpolation property. The term “tight” was introduced by Miller in [8], and the tight interpolation property has been considered in papers by Fuchs [3], Miller [8, 9], Loy and Miller [7] and Wirth [12]. If the closure 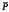of the cone P, in the interval topology, of such a partially ordered group G contains no pseudozeros, then 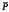is itself the cone of a partial order on G. Loy and Miller found of particular interest the case in which this associated partial orderis a lattice order. This situation was then considered in reverse by A. Wirth [12] who investigated under what circumstances a lattice ordered group would permit the existence of a tight Riesz order (called a compatible tight Riesz order) for which the initial lattice order is the order defined by the closure of the cone of the tight Riesz order.Wirth gave two fundamental anduseful characterizations of those subsets of the cone of a lattice ordered group that canbe the strict cone of a compatible tight Riesz order; one is in terms of archimedean classes and the other is an elementwise characterization. Although Loy, Miller and Wirth restricted their attention to abelian groups, much of what they do carries over verbatim to nonabelian groups. In the main result of this paper (Theorem 2.6) a description of the strict cone of a compatible tight Riesz order on a lattice ordered group Gis given in terms of the prime subgroups of G.This is particularly useful when one is attempting to identify the compatible tight Riesz orders on some particular lattice ordered group or class of lattice ordered groups, since it narrows down to a convenient family of subsets the possible candidates for strict cones of compatible tight Riesz orders. These can then be tested under Wirth's criteria. This technique is illustrated in § 5, where the compatible tight Riesz orders are determined o a lattice ordered group of the type V(Γ, Gγ), where Γ is of finite width, and in § 6, where two examples are considered.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 14 , Issue 2 , September 1973 , pp. 145 - 160
Copyright
Copyright © Glasgow Mathematical Journal Trust 1973

References

REFERENCES

1.Conrad, P., Introduction à la théorie des groupes réticulés, Université de Paris, 1967.Google Scholar
2.Conrad, P., Harvey, J. and Holland, C., The Hahn embedding theorem for abelian lattice ordered groups, Trans. Amer. Math. Soc. 108 (1963), 143–169.CrossRefGoogle Scholar
3.Fuchs, L., Approximation of lattice ordered groups, Ann. Univ. Sci. Budapest Eotvos. Sect. Math. (1965), 187–203.Google Scholar
4.Fuchs, L., Partially ordered algebraic systems (Oxford, 1963).Google Scholar
5.Holland, C., The lattice ordered group of automorphisms of anordered set, Michigan Math. J. 10 (1963), 399–408.CrossRefGoogle Scholar
6.Holland, C., Transitive lattice ordered groups, Math. Zeit. 87 (1965), 420–433.CrossRefGoogle Scholar
7.Loy, R. J. and Miller, J. B., Tight Riesz groups, J. Australian Math. Soc. 13 (1972), 224–240.CrossRefGoogle Scholar
8.Miller, J. B., Higher derivations on Banach algebras, Amer. J. Math, 92 (1970), 301–331.CrossRefGoogle Scholar
9.Miller, J. B., Tight Riesz groups and the Stone-Weierstrass theorem, J. Australian Math. Soc.; to appear.Google Scholar
10.Redfield, R., Doctoral Dissertation, Simon Fraser University (1972).Google Scholar
11.Riesz, F., Sur quelques notions fondamentales dans la theorie generale des operations lineaires, Ann. of Math. 41 (1940), 174–206.CrossRefGoogle Scholar
12.Wirth, A., Compatible tight Riesz orders, J. Australian Math. Soc. 15 (1973), 105–111.CrossRefGoogle Scholar