Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lamont, P. J. C.
1991.
Unique factorization in Cayley arithmetics and cryptology.
Glasgow Mathematical Journal,
Vol. 33,
Issue. 3,
p.
267.

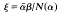 where
where 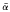 is the conjugate and
is the conjugate and 