Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T07:02:50.906Z Has data issue: false hasContentIssue false
  • English
  • Français

CONSTANT SCALAR CURVATURE HYPERSURFACES WITH SECOND-ORDER UMBILICITY

Published online by Cambridge University Press:  01 May 2009

ANTONIO GERVASIO COLARES  and
FERNANDO ENRIQUE ECHAIZ-ESPINOZA
ANTONIO GERVASIO COLARES
Affiliation:
Departamento de Matemática, Universidade Federal do Ceará, Campus do Pici, 60455-760 Fortaleza-CE, Brazil e-mail: gcolares@mat.ufc.br
FERNANDO ENRIQUE ECHAIZ-ESPINOZA
Affiliation:
Instituto de Matemática, Universidade Federal de Alagoas, Campus A.C. Simões, 57455-760 Maceió-AL, Brazil e-mail: echaiz@pos.mat.ufal.br
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We extend the concept of umbilicity to higher order umbilicity in Riemannian manifolds saying that an isometric immersion is k-umbilical when APk−1(A) is a multiple of the identity, where Pk(A) is the kth Newton polynomial in the second fundamental form A with P0(A) being the identity. Thus, for k=1, one-umbilical coincides with umbilical. We determine the principal curvatures of the two-umbilical isometric immersions in terms of the mean curvatures. We give a description of the two-umbilical isometric immersions in space forms which includes the product of spheres 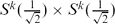embedded in the Euclidean sphere S2k+1 of radius 1. We also introduce an operator φk which measures how an isometric immersion fails to be k-umbilical, giving in particular that φ1 ≡ 0 if and only if the immersion is totally umbilical. We characterize the two-umbilical hypersurfaces of a space form as images of isometric immersions of Einstein manifolds.

Keywords

Primary 53C4253C40Secondary 53B2053B25
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 51 , Issue 2 , May 2009 , pp. 219 - 241
Copyright
Copyright © Glasgow Mathematical Journal Trust 2008

References

REFERENCES

1.Alencar, H. and do Carmo, M., Hypersurfaces with constant mean curvature in spheres, Proc. Am. Math. Soc. 120 (4) (1994), 1223–1229.CrossRefGoogle Scholar
2.Asperti, A. C. and Dajczer, M., N-dimensional submanifolds of ℝN+1 and S N+2, Illinois J. Math. 28 (4) (1984), 621–645.Google Scholar
3.Barbosa, J. L. and Colares, A. G., Stability of hypersurfaces with constant r-mean curvature, Ann. Global Anal. Geom. 15 (1997), 277–297.Google Scholar
4.Besse, A., Einstein Manifolds (Springer-Verlag, Berlin, 1987).CrossRefGoogle Scholar
5.Cartan, E., Familles de Surfaces Isoparamétriques dans les Espaces à Courbure Constant, Annali di Mat. 17 (1938), 177–191.CrossRefGoogle Scholar
6.Dajczer, M. and do Carmo, M., Rotation hypersurfaces in spaces of constant curvature, Trans. Am. Math. Soc. 277 (2) (1983), 685–709.Google Scholar
7.Dajczer, M. and Florit, L., On Chen's basic equality, Illinois J. Math. 42 (1) (1998) 97–106.Google Scholar
8.Fialkow, A., Hypersurfaces of a space of constant curvature, Ann. Math., 2nd Ser. 39 (4) (1938), 762–785.CrossRefGoogle Scholar
9.Otsuki, T., Minimal hypersurfaces in a Riemannian manifold of constant curvature, Am. J. Math. 92 (1970), 145–173.CrossRefGoogle Scholar
10.Reckziegel, H., On the problem whether the image of a given differentiable map into a Riemannian manifold is contained in a submanifold with parallel second fundamental form, J. Reine Angew. Math. 325 (1981), 87–104.Google Scholar
11.Walter, R., Compact hypersurfaces with a constant higher mean curvature function, Math. Ann. 270 (1985), 125–145.Google Scholar