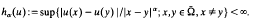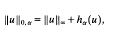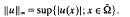Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Goebel, Manfred
1991.
On Fréchet-differentiability of Nemytskij operators acting in Hölder spaces.
Glasgow Mathematical Journal,
Vol. 33,
Issue. 1,
p.
1.
Goebel, Manfred
1992.
Continuity and Fr�chet-differentiability of Nemytskij operators in H�lder spaces.
Monatshefte f�r Mathematik,
Vol. 113,
Issue. 2,
p.
107.
de Cristoforis, Massimo Lanza
1994.
Higher order differentiability properties of the composition and of the inversion operator.
Indagationes Mathematicae,
Vol. 5,
Issue. 4,
p.
457.

 its closure.
its closure.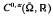 is the space of all functions
is the space of all functions 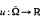 such that:
such that: