Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-15T15:20:48.618Z Has data issue: false hasContentIssue false
  • English
  • Français

A Counterexample in the theory of derivations

Published online by Cambridge University Press:  18 May 2009

Feng Wenying  and
Ji Guoxing
Feng Wenying
Affiliation:
Department of Mathematics, Shaanxi Normal University, Xi'an, People's Republic of China
Ji Guoxing
Affiliation:
Department of Mathematics, Shaanxi Normal University, Xi'an, People's Republic of China
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let B(H) be the algebra of all bounded linear operators on a separable, infinite dimensional complex Hilbert space H. Let C2 and C1 denote respectively, the Hilbert–Schmidt class and the trace class operators in B(H). It is known that C2 and C1 are two-sided*-ideals in B(H) and C2 is a Hilbert space with respect to the inner product

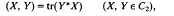
(where tr denotes the trace). For any Hilbert–Schmidt operator X let ∥X∥2=(X, X)½ be the Hilbert-Schmidt norm of X.

For fixed A ∈ B(H) let δA be the operator on B(H) defined by

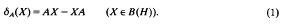
Operators of the form (1) are called inner derivations and they (as well as their restrictions 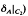have been extensively studied (for example [1–3]). In [1], Fuad Kittaneh proved the following result.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 31 , Issue 2 , May 1989 , pp. 161 - 163
Copyright
Copyright © Glasgow Mathematical Journal Trust 1989

References

1.Kittaneh, Fuad, On normal derivations of Hilbert-Schmidt type, Glasgow Math. J. 29 (1987), 245–248.CrossRefGoogle Scholar
2.Anderson, J. H., On normal derivations, Proc. Amer. Math. Soc. 38 (1973), 135–140.Google Scholar
3.Fialkow, L. A., A note on norm ideals and the operator, X → AX-XB, Israel J. Math. 32, (1979), 331–348.CrossRefGoogle Scholar
4.Williams, L. R., Quasisimilarity and hyponormal operators, j. Operator Theory 5 (1981), 127–139.Google Scholar