Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T06:32:36.814Z Has data issue: false hasContentIssue false
  • English
  • Français

DEGREE CONES AND MONOMIAL BASES OF LIE ALGEBRAS AND QUANTUM GROUPS

Published online by Cambridge University Press:  20 March 2017

TEODOR BACKHAUS ,
XIN FANG  and
GHISLAIN FOURIER
TEODOR BACKHAUS
Affiliation:
Mathematisches Institut, Universität zu Köln, Cologne, North Rhine-Westphalia, Germany e-mails: tbackha@math.uni-koeln.de, xinfang.math@gmail.com
XIN FANG
Affiliation:
Mathematisches Institut, Universität zu Köln, Cologne, North Rhine-Westphalia, Germany e-mails: tbackha@math.uni-koeln.de, xinfang.math@gmail.com
GHISLAIN FOURIER
Affiliation:
School of Mathematics and Statistics, University of Glasgow, United Kingdom Institut für Algebra, Zahlentheorie und Diskrete Mathematik, Leibniz Universität Hannover, Hannover, Lower Saxony, Germany e-mail: fourier@math.uni-hannover.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We provide ℕ-filtrations on the negative part Uq(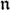$\mathfrak{n}$−) of the quantum group associated to a finite-dimensional simple Lie algebra 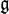$\mathfrak{g}$, such that the associated graded algebra is a skew-polynomial algebra on 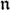$\mathfrak{n}$−. The filtration is obtained by assigning degrees to Lusztig's quantum PBW root vectors. The possible degrees can be described as lattice points in certain polyhedral cones. In the classical limit, such a degree induces an ℕ-filtration on any finite-dimensional simple 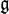$\mathfrak{g}$-module. We prove for type An, Cn, B3, D4 and G2 that a degree can be chosen such that the associated graded modules are defined by monomial ideals, and conjecture that this is true for any 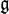$\mathfrak{g}$.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 59 , Issue 3 , September 2017 , pp. 595 - 621
Copyright
Copyright © Glasgow Mathematical Journal Trust 2017 

References

REFERENCES

1. Backhaus, T. and Desczyk, C., PBW filtration: Feigin-Fourier-Littelmann modules via Hasse diagrams, J. Lie Theory 25 (3) (2015), 815–856.Google Scholar
2. Backhaus, T. and Kus, D., The PBW filtration and convex polytopes in type B, to appear in Math. Z, arXiv:1504.06522.Google Scholar
3. Berenstein, A. and Zelevinsky, A., Tensor product multiplicities, canonical bases and totally positive varieties. Invent. Math. 143 (1) (2001), 77–128.CrossRefGoogle Scholar
4. Cerulli Irelli, G., Fang, X., Feigin, E., Fourier, G. and Reineke, M., Linear degenerations of flag varieties, arXiv:1603.08395.Google Scholar
5. Fang, X. and Fourier, G., Marked chain-order polytopes and string polytopes, Eur. J. Comb. 58 (November 2016), 267–282.CrossRefGoogle Scholar
6. Fang, X., Fourier, G. and Littelmann, P., Essential bases and toric degenerations arising from generating sequences, to appear in Adv. Math, arXiv:1510.02295.Google Scholar
7. Fang, X., Fourier, G. and Reineke, M., PBW-Filtration on quantum groups of type An , J. Algebra 449 (2016), 321–345.Google Scholar
8. Feigin, E., Fourier, G. and Littelmann, P., PBW filtration and bases for irreducible modules in type A n , Transform. Groups 16 (1) (2011), 71–89.Google Scholar
9. Feigin, E., Fourier, G. and Littelmann, P., PBW filtration and bases for symplectic Lie algebras, Int. Math. Res. Not. IMRN 24 (2011), 5760–5784.CrossRefGoogle Scholar
10. Feigin, E., Fourier, G. and Littelmann, P., Favourable modules: Filtrations, polytopes, Newton-Okounkov bodies and flat degenerations, Transform. Groups, 2016, DOI: 10.1007/S00031-016-9389-2.Google Scholar
11. Gawrilow, E. and Joswig, M., Polymake: A framework for analyzing convex polytopes. Polytopes – combinatorics and computation (Oberwolfach, 1997), DMV Sem., 29 (Birkhäuser, Basel, 2000), 43–73.Google Scholar
12. Gornitskii, A. A., Essential signatures and canonical bases of irreducible representations of the group G 2 , Math. Notes 97 (1) (2015), 30–41.CrossRefGoogle Scholar
13. Gornitskii, A. A., Essential signatures and canonical bases of irreducible representations of D 4, preprint, arXiv:1507.07498.Google Scholar
14. Kashiwara, M., On crystal bases of the q-analogue of universal enveloping algebras, Duke Math. J. 63 (1991), 465–516.Google Scholar
15. Kiritchenko, V., Geometric mitosis, Math. Res. Lett. 23 (4) (2016), 1069–1096.CrossRefGoogle Scholar
16. Kiritchenko, V., Newton–Okounkov polytopes of flag varieties, to appear in Transform. Groups, DOI:10.1007/s00031-016-9372-y.CrossRefGoogle Scholar
17. Littelmann, P., Cones, crystals, and patterns, Transform. Groups 3 (2) (1998), 145–179.Google Scholar
18. Lusztig, G., Canonical bases arising from quantized enveloping algebras, J. Amer. Math. Soc. 3 (2) (1990), 447–498.CrossRefGoogle Scholar
19. Lusztig, G., Introduction to quantum groups. Reprint of the 1994 edition. Modern Birkhäuser Classics (Birkhäuser/Springer, New York, 2010).CrossRefGoogle Scholar
20. Papi, P., A characterization of a special ordering in a root system. Proc. Amer. Math. Soc. 120 (3) (1994), 661–665.Google Scholar