Dehn functions of mapping tori of right-angled Artin groups

Abstract

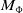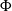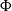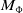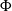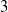The algebraic mapping torus $M_{\Phi }$ of a group $G$ with an automorphism $\Phi$ is the HNN-extension of $G$ in which conjugation by the stable letter performs $\Phi$. We classify the Dehn functions of $M_{\Phi }$ in terms of $\Phi$ for a number of right-angled Artin groups (RAAGs) $G$, including all $3$-generator RAAGs and 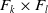$F_k \times F_l$ for all 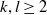$k,l \geq 2$.

1. Our results

When studying mapping tori, a natural question is how the maps used to define them determine their geometry. The paradigm is the Nielsen–Thurston classification. If $S$ is a compact orientable surface of genus at least $2$ and $f\;:\;S \to S$ is a homeomorphism, then the mapping torus $M_f$ is $(S \times [0,1])/ \!\! \sim$ where $(x, 1) \sim (f(x),0)$ for all $x \in S$ . The classification states that up to isotopy $f$ is exactly one of reducible, periodic, or pseudo-Anosov and, accordingly, contains an incompressible torus, admits an $\mathbb{H}^2 \times \mathbb{R}$ structure, or admits a hyperbolic structure.

Algebraic mapping tori are fundamental groups of topological mapping tori of surfaces or complexes. For a finitely presented group $G= \langle X \! \mid \! R \rangle$ and an injective endomorphism $\Phi \;:\; G \to G$ , the algebraic mapping torus is the group:

\begin{equation*}M_{\Phi } \ \;:\!=\; \ \langle X, t \mid {R}, \ t^{-1}xt= \Phi (x),\, \forall x \in X \rangle .\end{equation*}

In this article, $\Phi$ will always be an automorphism, so $M_{\Phi } = G \rtimes _{\Phi } \mathbb{Z}$ , and $G$ will always be a right-angled Artin group (“RAAG”)—that is, $G$ is encoded by a finite graph $\Gamma$ with vertex set $X$ in that $G$ is presented by:

\begin{equation*}\langle X \mid uv=vu \text { when } (u, v) \text { is an edge in } \Gamma \rangle .\end{equation*}

We will study $M_{\Phi }$ via their Dehn functions (which we will always consider qualitatively—that is, up to an equivalence relation $\simeq$ : for $f,g\;:\; \mathbb{N} \to \mathbb{N}$ , write $f\preceq g$ when there exists $C\gt 0$ such that $f(n) \leq Cg(Cn+C) +Cn+C$ for all $n \in \mathbb{N}$ , and write $f \simeq g$ when $f \preceq g$ and $g \preceq f$ ). The Dehn function is an invariant of finitely presentable groups. It can be viewed either as an algorithmic complexity measure for the word problem or as an isoperimetric function recording the minimal area of disks spanning loops as a function of the lengths of the loops. More details are in Section 3.1.

Our study is motivated by the following two classifications. The first concerns $G=\mathbb{Z}^k$ , the RAAG associated with the complete graph with $k$ vertices.

Theorem (Bridson–Gersten, Main Theorem [7], Bridson–Pittet, Theorem 5.1 [10]). If $\Phi \in{\textrm{Aut}}(\mathbb{Z}^k)\,=\,\textrm{GL}(k,\mathbb{Z})$ has an eigenvalue $\lambda$ with $|\lambda | \neq 1$ , then the Dehn function of the mapping torus $M_{\Phi }$ is exponential. Else, the Dehn function of $M_{\Phi }$ is polynomial of degree $c+1$ , where $c \times c$ is the size of the largest Jordan block in the Jordan Canonical form of the matrix associated with $\Phi$ .

The second classification concerns $G=F_k$ , the rank- $k$ free group, that is, the RAAG associated with the graph with $k$ vertices and no edges. An automorphism $\Phi$ of $F_k$ is atoroidal when there are no periodic conjugacy classes—equivalently, for all $w \in F_k$ and $n \in \mathbb{Z}$ , if $w$ and $\Phi ^n(w)$ are conjugate, then $w=1$ or $n=0$ .

Theorem (Bestvina–Handel [3], Brinkmann [11], Bridson–Groves [8]). Suppose $\Phi \in{\textrm{Aut}}(F_k)$ . The mapping torus $M_{\Phi }$ is hyperbolic (i.e. has linear Dehn function) if and only if $\Phi$ is atoroidal. All other $M_{\Phi }$ have quadratic Dehn functions.

RAAGs interpolate between free abelian groups and free groups, so it is natural to look to extend the above theorems to other RAAGs. We thank Karen Vogtmann for suggesting this problem to us.

A classification of the Dehn functions of all RAAGs remains out of reach. Here, we complete the classification for three-generator RAAGs and all groups $F_k \times F_l$ where $k,l \geq 2$ .

For $\mathbb{Z}^3$ and $F_3$ and for all RAAGs on fewer than $3$ generators, the theorems above classify the Dehn functions of $M_{\Phi }$ . Here are our results on the remaining three-generator RAAGs, namely $F_2 \times \mathbb{Z}$ and $\mathbb{Z}^2 \ast \mathbb{Z}$ .

If $\Psi \in{\textrm{Aut}}(F_2 \times \mathbb{Z})$ , then $\Psi = \psi \times \rho$ where $\psi \in{\textrm{Aut}}(F_2)$ and $\rho \;:\; \mathbb{Z} \to \mathbb{Z}$ is the identity or the map $r \mapsto -r$ .

Theorem A. Suppose $\Psi \in{\textrm{Aut}}(F_2 \times \mathbb{Z})$ induces $\psi \in{\textrm{Aut}}(F_2)$ . Let $\psi _{ab} \in{\textrm{Aut}}(\mathbb{Z}^2)$ be the map induced by $\psi$ via the abelianization map $F_2 \to \mathbb{Z}^2$ , $g \mapsto g_{ab}$ .

Let $p\;:\; F_2 \times \mathbb{Z} \to \mathbb{Z}$ be the projection map $p(g,r) =r$ . Exactly one of the following holds:

1. 1. There exists $g \in F_2$ and $m \in \mathbb{N}$ such that $\psi _{ab}^m(g_{ab}) = g_{ab}$ and $p(\Psi ^m(g)) \neq 0$ , in which case $M_{\Psi }$ has cubic Dehn function.

2. 2. $M_{\Psi }$ has quadratic Dehn function.

Theorem B. Suppose $\Psi \in{\textrm{Aut}}(\mathbb{Z}^2 \ast \mathbb{Z})$ . Suppose $\Phi \in{\textrm{Aut}}(\mathbb{Z}^2 \ast \mathbb{Z})$ restricts to an automorphism $\phi$ on the $\mathbb{Z}^2$ factor and satisfies $[\Psi ] = [\Phi ] \in \textrm{Out}(\mathbb{Z}^2 \ast \mathbb{Z})$ . Exactly one of the following holds:

1. 1. $\phi$ is of finite order, in which case $M_{\Psi }$ has quadratic Dehn function.

2. 2. $\phi$ has an eigenvalue $\lambda$ such that $|\lambda | \neq 1$ , in which case $M_{\Psi }$ has exponential Dehn function.

3. 3. $M_{\Psi }$ has cubic Dehn function.

Theorem B is effective in that, given a $\Psi$ , a $\Phi$ as per the statement can be produced: see Lemma 6.1.

Suppose $F$ is a free group with a finite basis $X$ . For $x\in F$ , $|x|$ denotes the length of the reduced word on $X^{\pm 1}$ representing $x$ . The growth $g_{\Phi, X}\;:\; \mathbb{N} \to \mathbb{N}$ of an automorphism $\Phi \;:\;F \to F$ is defined by $g_{\Phi, X}(n) \;:\!=\; \max _{x\in X}\{|\Phi ^n(x)|\}$ . While the growth type of $g_{\Phi, X}$ does not depend on the choice of $X$ , it is not invariant under inner automorphisms. For example, the automorphism $\phi \;:\;a \mapsto b^{-1}ab,\,\, b \mapsto b$ has linear growth, whereas $\psi \;:\;a \mapsto a,\,\, b\mapsto b$ has constant growth. The cyclic growth $g_{\Phi }^{cyc}$ of an automorphism accounts for this. It describes the growth of (all) conjugacy classes under iteration of automorphisms and is invariant under inner automorphisms. Details are in Section 7.2.

We classify the Dehn functions of mapping tori of products $F_k \times F_l$ of free groups with $k,l \geq 2$ . This theorem is effective: in Section 7.1, we explain how to compute $\phi _1$ and $\phi _2$ from $\Psi$ .

Theorem C. If $G= F_k \times F_l,$ where $k,l \geq 2$ , and $\Psi \in{\textrm{Aut}}(F_k \times F_l)$ , then we can find $\phi _1 \in{\textrm{Aut}}(F_k)$ and $\phi _2 \in{\textrm{Aut}}(F_l)$ such that $\Phi = \phi _1 \times \phi _2$ satisfies $[\Phi ] = [\Psi ^2]$ in $\textrm{Out}(F_k \times F_l)$ . The Dehn functions of the associated mapping tori satisfy $\delta _{M_{\Phi }} \simeq \delta _{M_{\Psi }}$ and their asymptotics can be read off $\phi _1$ and $\phi _2$ in that:

1. 1. If $[\phi _i^p] = [\textrm{Id}] \in \textrm{Out}(F_k)$ for some $p\in \mathbb{N}$ , and $i$ is either $1$ or $2$ , then $\delta _{M_{\Psi }}(n) \simeq n^2$ .

2. 2. If $n^{d_1} \simeq g_{\phi _1}^{cyc}(n) \preceq g_{\phi _2}^{cyc}(n)$ for some $d_1 \geq 1$ , then $\delta _{M_{\Psi }}(n) \simeq n^{d_1+2}$ , and likewise with the indices $1$ and $2$ interchanged.

3. 3. If $g_{\phi _1}^{cyc}(n) \simeq g_{\phi _2}^{cyc}(n) \simeq 2^n$ , then $\delta _{M_{\Psi }}$ grows exponentially.

As we will explain in Section 7.2, the three cases in Theorem C are exhaustive and mutually exclusive.

Since all automorphisms of $F_2$ are periodic or have cyclic growth, that is, linear or exponential, this implies:

Corollary D. If $G= F_2 \times F_2,$ and $\Psi \in{\textrm{Aut}}(G)$ , then $M_{\Psi }$ has quadratic, cubic, or exponential Dehn function.

We are also able to determine the Dehn functions of mapping tori of $F_k \times \mathbb{Z}$ in some cases. In Section 8, we detail these cases, remark on the limits of our techniques, and suggest next steps in this line of research.

2. Overview

This article is organized as follows. In Section 3, we give background on Dehn functions and on corridors in van Kampen diagrams. In Section 4, we review the electrostatic model of Gersten and Riley from [16]. We prove Theorems A, B, and C in Sections 5, 6, and 7, respectively.

Here is an outline of our strategy. Given a RAAG $G$ , we organize its automorphisms $\Phi$ into cases, chosen so that within each case we can present $M_{\Phi }$ in a manner which facilitates analysis of its Dehn function. In some cases, we find it convenient to replace $\Phi$ by a power; this, in turn, replaces $M_{\Phi }$ by a finite index subgroup, which does not qualitatively change the Dehn function.

In the setting of Theorem A, our presentation expresses $M_{\Phi }$ as a central extension of another mapping torus $M_{\phi }$ . Then, we use what Gersten and Riley called an electrostatic model in [16] to get upper bounds on the Dehn function of $M_{\Phi }$ . The idea is that a van Kampen diagram over $M_{\phi }$ can be “charged” by elements of the kernel of the extension (elements of the center of $M_{\Phi }$ ). The diagram is then “inflated” by adding in suitable corridors to connect up these charges and get a van Kampen diagram over $M_{\Phi }$ . This leads to diagrams of cubic area (as a function of their boundary length) and so a cubic upper bound on the Dehn function. For certain $\Phi$ , we improve this estimate to quadratic by noticing that $M_{\phi }$ is hyperbolic relative to a $\mathbb{Z}^2$ subgroup that receives no charges. This implies that only linearly many charges appear in the diagram, and thereby that the resulting van Kampen diagram over $M_{\Phi }$ has quadratic area. For other $\Phi$ , we define partial corridors in van Kampen diagrams and then use Hall’s Marriage Theorem to give a special pattern for discharging the diagrams, which again improves the Dehn function upper bound to quadratic.

As for obtaining the matching lower bounds, the Dehn function of $M_{\Phi }$ is always at least quadratic because $M_{\Phi }$ is not hyperbolic. For certain $M_{\Phi }$ , a result of Bridson and Gersten (see Lemma 3.5) improves this to a cubic lower bound by identifying a suitable quasi-isometrically embedded abelian subgroup of $G$ to which the action of $\Phi$ restricts.

For Theorem B the main innovation is for a case where, even though the $M_{\Phi }$ are not central extensions, one generator $b$ commutes with all other generators apart from one generator $c$ . That $c$ forms corridors in van Kampen diagrams over the quotient of $M_{\Phi }$ obtained by killing $b$ , and the electrostatic model applies to regions complementary to the $c$ -corridors. We then define alternating corridors which string together two types of partial corridors, and we show that these alternating corridors can intersect themselves and each other at most once, and that every 2-cell in the diagram is contained in some alternating corridor. This lets us prove that the area of the van Kampen diagram in the quotient is at most quadratic in the length of the boundary word. The electrostatic model then produces a van Kampen diagram with at most cubic area.

For the lower bounds of Theorem C, we exhibit a family of words such that any van Kampen diagram for one of these words has area we can bound below on account of having a belt of corridors of controlled length. For the upper bound, we estimate the number of relators that need to be applied to convert a word $w$ representing the identity over the mapping torus of $F_k \times F_l$ to a word $v$ with $|v| \leq |w|$ that represents the identity in $F_k \rtimes _{\phi _1} \mathbb{Z}$ and then we use the fact that the Dehn function of $F_k \rtimes _{\phi _1} \mathbb{Z}$ is at most quadratic. The upper and lower bounds on the Dehn function are derived from two different notions of free group automorphism growth, which we reconcile by appealing to a number of results in the literature.

3. Preliminaries

We write $\left |w\right |$ to denote the length of a word $w$ . Our conventions are $a^t \;:\!=\; t^{-1} a t$ and $[a,b] \;:\!=\; a^{-1} b^{-1} a b$ .

3.1. Van Kampen diagrams, corridors, and Dehn functions

These topics feature in many surveys, for instance, Section III.H.2 in [9]. Here are the essentials.

Suppose $G=\langle X \! \mid \! R \rangle$ is a finitely presented group (so $R$ is a finite set of words on a finite alphabet $X$ and its inverse letters). Suppose $w$ is a word on $X \cup X^{-1}$ such that $w=1$ in $G$ . A van Kampen diagram $\Delta$ for $w$ is a simply connected planar 2-complex with edges labeled by elements of $X$ and directed so that the following holds. When traversing $\partial \Delta$ counterclockwise from some base vertex, we read off $w$ , and around the boundary of each 2-cell in one direction or the other and from a suitable base vertex, we read an element of $R$ . (If an edge is traversed in the direction of its orientation, the positive generator is implied, and if against its orientation, the inverse of the generator.) The 1-skeleton $\Delta ^{(1)}$ of $\Delta$ has the path metric in which every edge has length 1. The area of $\Delta$ is the number of 2-cells it has. $\textrm{Area}(w)$ denotes the minimum area among all van Kampen diagrams with boundary word $w$ .

The Dehn function $\delta \;:\;\mathbb{N} \to \mathbb{N}$ of $\langle X \! \mid \! R \rangle$ is $ \delta (n) \;:\!=\; \max \{\textrm{Area}(w) \mid \left |w\right | \leq n \text{ and } w =1 \text{ in } G \}$ .

Up to the equivalence relation $\simeq$ defined in Section 1, the Dehn function does not depend on the choice of finite presentation for $G$ and, moreover, is a quasi-isometry invariant among finitely presented groups. In particular, we will need:

Proposition 3.1. If $G$ is finitely presented and $H\leq G$ is a finite index subgroup, then $H$ is also finitely presentable and $G$ and $H$ have equivalent Dehn functions.

Corridors appear in van Kampen diagrams over a presentation $\langle X \! \mid \! R \rangle$ when there is some $a \in X$ such that all relators $r \in R$ in which $a$ appears can be expressed as $w_1a^{\pm 1}w_2a^{\mp 1}w_3$ where $w_1$ , $w_2$ , and $w_3$ are words not containing $a^{\pm 1}$ . Such presentations naturally arise for HNN-extensions, with $a$ being the stable letter. Suppose $\Delta$ is a van Kampen diagram for a word $w$ over such a presentation. If there is an $a$ -edge (an edge labeled $a$ ) in $\Delta$ and there is a 2-cell in $\Delta$ with that edge in its boundary, then that 2-cell will have exactly one other $a$ -edge, and that $a$ -edge will either be in the boundary or will be in the boundary of another 2-cell. Concatenations of 2-cells in $\Delta$ across $a$ -edges in this manner are called corridors. A corridor either connects a pair of $a$ -edges in the boundary of $\Delta$ or closes up to form an annulus. The $a$ and $a^{-1}$ that label edges in the boundaries of the two-dimensional parts (Figure 1b) of $\Delta$ are paired off and connected by corridors. The number of 2-cells involved is the length of the corridor. An $a$ -corridor is reduced if it contains no back-to-back canceling pair of 2-cells—that is, no two 2-cells sharing an $a$ -edge for which the word around the boundary of their union is freely reducible to the identity in the group. If an $a$ -corridor is the concatenation of $2$ -cells labeled $u_1 a v_1^{-1} a^{-1}$ , …, $u_r a v_r^{-1} a^{-1}$ , then the top (respectively, bottom) of that corridor is the path that is labeled $v_1 \cdots v_r$ (respectively, $u_1 \cdots u_r$ ) and passes through the terminal (respectively, initial) vertices of the $a$ -edges—see Figure 1c.

Figure 1. Corridors.

Remark 3.2. Many of the presentations we will work with will have the form $\langle X, a \mid R, \ x^a = w_x; \ x \in X \rangle$ where $X$ is some alphabet (not containing $a$ ), and $R$ and $\left \{w_x \mid x \in X\right \}$ are sets of words on $X^{\pm 1}$ . An $a$ -corridor in a diagram over such a presentation is reduced exactly when the word along the bottom is reduced.

Suppose $\Delta$ is a van Kampen diagram with $N$ $a$ -corridors. Then $N$ is at most half the length of the boundary (at most half the number of $a^{\pm 1}$ in $w$ ). Since $a$ -corridors cannot cross, removing all the $a$ -corridors leaves $N+1$ connected subdiagrams called $a$ -complementary regions. The words around the perimeters of each of these regions contain no $a^{\pm 1}$ . Therefore, analysis of the lengths of the $a$ -corridors and of the areas of the $a$ -complementary regions can lead to estimates on the area of $\Delta$ .

The dual tree to the set of $a$ -corridors has vertices corresponding to $a$ -complementary regions and has an edge between two vertices when an $a$ -corridor borders the two corresponding $a$ -complementary regions. (There is no vertex corresponding to the outside of the van Kampen diagram.)

Definition 3.3. A letter $a$ forms partial corridors when all the defining relations which contain both $a$ and $a^{-1}$ have the form of a corridor relation, $a^{\pm 1} wa^{\mp 1}=w^{\prime }$ for words $w$ and $w^{\prime }$ without $a$ or $a^{-1}$ . A partial corridor is a maximal concatenation of 2-cells joined by common $a$ -edges as above. We refer to such 2-cells which contain one or more $a$ or $a^{-1}$ (but not both) in their boundary words as capping faces, since they cap off partial corridors.

An $a$ in the boundary of a van Kampen diagram will either be connected by a full $a$ -corridor to another edge labeled by $a$ in the boundary, or it begins a partial $a$ -corridor ending at one of the capping faces. An $a$ -edge on a capping face is connected via a partial $a$ -corridor (possibly of length zero) either to the boundary or to an $a$ -edge of another capping face.

Like standard corridors, partial corridors cannot cross. However, there is no immediate control on the number of partial corridors in terms of $|w|$ , since they may begin and end in capping faces within the diagram.

3.2. General bounds on Dehn functions of mapping tori of RAAGs

RAAGs are (bi)automatic [17, 25], so have either linear or quadratic Dehn functions. A finitely presented group is hyperbolic if and only if it has linear Dehn function. Finite-rank free groups are hyperbolic. Non-free RAAGs have $\mathbb{Z}^2$ subgroups and so are not hyperbolic (e.g. [9]). So RAAGs have either linear or quadratic Dehn functions, the linear case only occurring for free RAAGs. This will be useful for the following lemma.

Lemma 3.4. If $G$ is a non-free RAAG and $\Psi \in{\textrm{Aut}}(G)$ , then the Dehn function of $M_{\Psi }$ satisfies $n^2 \preceq \delta (n) \preceq 2^n$ .

Proof. Suppose $G$ is a non-free RAAG. So $G$ has a finite presentation $\langle X \! \mid \! R \rangle$ derived from a graph with at least one edge. Then $G$ and hence $M_{\Psi }$ will contain a $\mathbb{\mathbb{Z}}^2$ subgroup. This implies that $M_{\Psi }$ is not hyperbolic and therefore $n^2 \preceq \delta (n)$ (again, e.g. [9]).

A word $w$ on the generators of

\begin{equation*}M_{\Psi } \ = \ \langle X, t \mid {R}, \ t^{-1}xt= \Psi (x),\, \forall \, x \in X \rangle \end{equation*}

can be expressed as $t^{k_0}a_1t^{k_1}\cdots a_mt^{k_m}$ for some $a_1, \ldots, a_m \in X^{\pm 1}$ and some $k_1, \ldots, k_m \in \mathbb{Z}$ . Suppose $w$ represents the identity in $M_{\Psi }$ . Then shuffling all the $t^{\mp 1}$ to the right, replacing each $a_i$ by the freely reduced word representing $\Psi ^{\pm 1}(a_i)$ does not change the element of $M_{\Psi }$ represented. Eventually, we arrive at $u t^{k_0 + \cdots + k_m}$ where $u$ is a word on $X^{\pm 1}$ that represents $1$ in $G$ and $k_0 + \cdots + k_m =0$ . Applying $\Psi ^{\pm 1}$ to a letter in $X^{\pm 1}$ increases its length by at most the factor $C\;:\!=\;\max _{a \in X} |\Psi ^{\pm 1}(a)|$ . So $m C^{\left |k_0\right |+ \cdots + \left |k_m\right |} \leq \left |w\right | C^{\left |w\right |}$ is an upper bound for both $\left |u\right |$ and for the number of relation applications needed to convert $w$ to $u$ .

The Dehn function of $G$ is at most quadratic, so $u$ can be reduced to the empty word using at most a constant times $\left |u\right |^2$ defining relations. Thus $\textrm{Area}(w)$ is at most a constant times $\left |w\right | C^{\left |w\right |} + (\left |w\right | C^{\left |w\right |})^2$ , and therefore (since $\alpha ^n \simeq \beta ^n$ for all $\alpha, \beta \gt 1$ ) we deduce $\delta (n) \preceq 2^n$ .

Our next lemma is the special case of Theorem 4.1 of [7] in which, in the notation of [7], $G=H$ and $K$ is quasi-isometrically embedded. We will call on it repeatedly to establish lower bounds on the Dehn functions.

Lemma 3.5 (Adapted from Theorem 4.1 of Bridson–Gersten [7]). Suppose $K = \langle k_1, \dots, k_m \rangle$ is a quasi-isometrically embedded infinite abelian subgroup of a finitely presented group $G$ . If $\Phi \in{\textrm{Aut}}(G)$ and $\Phi (K) = K$ , then the Dehn function $\delta$ of $\langle G, t\, |\, g^t=\Phi (g) \rangle$ satisfies

\begin{equation*}{n^2\max _{1 \leq i \leq m}{ \left |\Phi ^{\pm n}(k_i)\right |} \ \preceq \ \delta (n)}.\end{equation*}

Equivalently, suppose $\phi = \Phi \left |_{K} \right .$ is associated to the matrix $A$ ; then

1. 1. If $\phi$ has an eigenvalue $\lambda$ such that $|\lambda | \neq 1$ , then $M_{\Phi }$ has exponential Dehn function.

2. 2. If $\phi$ only has eigenvalues $\lambda$ such that $|\lambda |=1$ , then $n^{c+1} \preceq \delta (n)$ , where the size of the largest Jordan block for $A$ is $c \times c$ .

The following lemma allows us to specialize to convenient $\Psi$ when analyzing the Dehn functions of mapping tori. We include the proof because it is brief and the result is vital to this paper.

Lemma 3.6 (c.f. Lemma 2.1 of [4]). The following mapping tori have equivalent Dehn functions:

1. 1. $M_{\Psi }$ and $M_{\Psi ^n}$ , for any $n \in \mathbb{N}$ .

2. 2. $M_{\Psi }$ and $M_{\Psi ^{-1}}$ .

3. 3. $M_{\Psi _1}$ and $M_{\Psi _2}$ when $\Psi _1$ and $\Psi _2$ are conjugate in $\textrm{Out}(G)$ .

Proof, based on [4]. Map $M_{\Psi }$ onto $\langle t \rangle = \mathbb{Z}$ by killing $G$ and then onto $\mathbb{Z}/n\mathbb{Z}$ by the natural quotient map. The kernel of this composition is the index- $n$ subgroup $M_{\Psi ^n}$ . By Proposition 3.1, $M_{\Psi }$ and $M_{\Psi ^n}$ have equivalent Dehn functions.

As $w^t = \Psi (w)$ for all $w \in G$ , it follows that $w^{t^{-1}} = \Psi ^{-1}(w)$ , so mapping $t \mapsto t^{-1}$ and fixing $G$ gives an isomorphism $M_{\Psi } \to M_{\Psi ^{-1}}$ . Thus, $M_{\Psi }$ and $M_{\Psi ^{-1}}$ have equivalent Dehn functions.

If $\Psi _1$ and $\Psi _2$ are conjugate in $\textrm{Out}(G)$ , there exists $\eta \in{\textrm{Aut}}(G)$ and $h\in G$ such that $\Psi _2(g) = \eta ^{-1}(\Psi _1(\eta (g^h)))$ for all $g \in G$ . We will show that $M_{\Psi _1}$ and $M_{\Psi _2}$ are isomorphic. Consider $F\;:\;M_{\Psi _2} \to M_{\Psi _1}$ given by $x \mapsto \eta (x)$ for $x \in G$ and $t \mapsto t\,\hat{h}$ , where $\hat{h}\;:\!=\;\Psi _1(\eta (h))$ . It is a homomorphism because the relators $(g^{-1})^t\Psi _2(g)$ for $g \in G$ are mapped to the identity in $M_{\Psi _1}$ , since $(w^{-1})^t\Psi _1(w)=1$ in $M_{\Psi _1}$ for $w \in G$ . Indeed,

\begin{eqnarray*} F\left ((g^{-1})^t\Psi _2(g)\right ) \ = \ F\left ((g^{-1})^t\eta ^{-1}(\Psi _1(\eta (g^h)))\right ) \ = \ \eta (g^{-1})^{t\hat{h}}\Psi _1( \eta (g^h)) \\[5pt] \ = \ (\eta (g^{-1}))^{t\hat{h}} \Psi _1(\eta (g))^{\hat{h}} \ = \ \left ((w^{-1})^{t} \Psi _1(w)\right )^{\hat{h}} \ = \ 1^{\hat{h}} \ = \ 1. \end{eqnarray*}

where $w=\eta (g)$ . It is certainly onto. This homomorphism has inverse given by $x \mapsto \eta ^{-1}(x)$ for $x \in G$ and $t \mapsto t\,\eta ^{-1}(\hat{h}^{-1})$ , so it is an isomorphism.

3.3. Growth and automorphisms of $\mathbb{Z}^2$

Let $||A||$ denote the maximum of the absolute values of the entries in a matrix $A \in \textrm{GL}(2, \mathbb{Z}) ={\textrm{Aut}}(\mathbb{Z}^2)$ . We say $A$ has linear growth when the function $\mathbb{N} \to \mathbb{N}$ mapping $n \mapsto ||A^n||$ is $\simeq$ -equivalent to $n \mapsto n$ .

The following lemmas will allow us to specialize to convenient cases of $\Phi$ when analyzing Dehn functions of mapping tori $M_{\Phi }$ of $F_2 \times \mathbb{Z}$ and $\mathbb{Z}^2 \ast \mathbb{Z}$ .

Lemma 3.7. If $A \in \textrm{SL}(2, \mathbb{Z})$ has linear growth, then there are integers $\alpha$ and $k$ such that $k\gt 0$ and $A^k$ is conjugate to $\left (\begin{smallmatrix} 1 & \alpha \\[5pt] 0 & 1 \end{smallmatrix}\right )$ in $\textrm{SL}(2,\mathbb{Z})$ .

Proof. As $A$ has linear growth, Theorem 2.1 of [7] tells us that there exists an integer $k \gt 0$ such that $A^k$ is $I+N$ for some nonzero matrix $N$ such that $N^2=0$ . As $N^2=0$ , the trace of $N$ is zero, and $N=\left ( \begin{smallmatrix} a & b \\[5pt] c & -a\\[5pt] \end{smallmatrix}\right )$ for some integers $a, b, c$ not all zero such that $a^2 = -bc$ . If $a=c=0$ , then the result holds with $\alpha =b$ . So assume they are not both zero. Notice that $N \left (\begin{smallmatrix} a \\[5pt] c \end{smallmatrix}\right ) = \left (\begin{smallmatrix} 0 \\[5pt] 0 \end{smallmatrix}\right )$ . So there are coprime integers $p$ and $q$ (in particular not both zero) with $N \left (\begin{smallmatrix} p \\[5pt] q \end{smallmatrix}\right ) = \left (\begin{smallmatrix} 0 \\[5pt] 0 \end{smallmatrix}\right )$ . By Bézout, there are $r, s \in \mathbb{Z}$ such that $ps-qr=1$ , and so $B\;:\!=\; \left (\begin{smallmatrix} p & r \\[5pt] q & s \end{smallmatrix}\right )$ is in $\textrm{SL}(2, \mathbb{Z})$ . And then ${B}^{-1}NB = \left (\begin{smallmatrix} 0 & \alpha \\[5pt] 0 & 0 \end{smallmatrix}\right )$ where $\alpha = 2ars +bs^2 -cr^2$ , and the result follows.

Lemma 3.8. Suppose $A \in \textrm{SL}(2, \mathbb{Z})$ has a non-real eigenvalue $\lambda =x+ yi$ , then it has order dividing 6.

Proof. As $A \in \textrm{SL}(2, \mathbb{Z})$ we can say $\det (A)=1 =(x+yi)(x-yi)=x^2+y^2$ , so $|\lambda |=1$ and $\lambda ^2-\mbox{tr}(A) \lambda +1 =0$ . Since $\lambda$ is not real, the discriminant $\mbox{tr}(A)^2-4\lt 0$ , and as $A$ has only integer entries, $\mbox{tr}(A)\in \{0, \pm 1\}$ . Then, as $\mbox{tr}(A)= 2x$ , we find $x \in \{0, \pm \frac{1}{2}\}$ . It follows that $A$ is conjugate in $\textrm{SL}(2,{\mathbb{C}})$ to $\left ( \begin{smallmatrix} e^{i\theta } & 0 \\[5pt] 0 & e^{-i \theta } \\[5pt] \end{smallmatrix} \right )$ , where $\theta$ is $\pm \pi/2$ , $\pm 2\pi/3$ , or $\pm \pi/3$ , and so $A$ has order dividing $6$ .

Lemma 3.9. $A \in \textrm{SL}(2, \mathbb{Z})$ has real non-unit eigenvalues if and only if $A$ grows exponentially.

Proof. If $A \in \textrm{SL}(2, \mathbb{Z})$ has real non-unit eigenvalues, then $A$ has two eigenvalues $\lambda$ and $\lambda ^{-1}$ , where $|\lambda |\gt 1$ . It follows that $A$ is conjugate in $\textrm{SL}(2,{\mathbb{C}})$ to $\left ( \begin{smallmatrix} \lambda & 0 \\[5pt] 0 & \lambda ^{-1} \\[5pt] \end{smallmatrix} \right )$ . By taking powers of the diagonalization in $\textrm{SL}(2,{\mathbb{C}})$ , $A^k=PD^kP^{-1} =\left ( \begin{smallmatrix} a & b \\[5pt] c & d \\[5pt] \end{smallmatrix} \right )\left ( \begin{smallmatrix} \lambda ^k & 0 \\[5pt] 0 & \lambda ^{-k} \\[5pt] \end{smallmatrix} \right )\frac{1}{ad-bc}\left ( \begin{smallmatrix} d & -b \\[5pt] -c & a \\[5pt] \end{smallmatrix} \right )$ , we can see that $A$ has exponential growth.

For the converse, suppose $A$ grows exponentially. By Lemma 3.8, it has real eigenvalues. Its eigenvalues cannot be both $1$ or both $-1$ because then $A^2$ would be conjugate in $\textrm{SL}(2,{\mathbb{C}})$ to a matrix of linear growth (as in Lemma 3.7).

4. The electrostatic model for central extensions

Gersten and Riley’s electrostatic model is a method of constructing van Kampen diagrams for central extensions (Proposition 6.1 of [16]). We will use it and variants to obtain upper bounds on the Dehn functions of some mapping tori.

Suppose a group $\Gamma$ is a central extension $1 \to \mathbb{Z} \to{\Gamma } \to \overline{\Gamma } \to 1$ with kernel $\mathbb{Z} = \langle c \rangle$ . If $\overline{\Gamma }$ has presentation

\begin{equation*}\mathcal {P}_{\overline {\Gamma }} \ = \ \langle X \! \mid \! r_1= \cdots = r_n=1 \rangle,\end{equation*}

then for some $k_1, \ldots, k_n \in \mathbb{Z}$ , $\Gamma$ has presentation:

\begin{equation*}{\mathcal {P}_{\Gamma } \ = \ \langle X, c \mid r_1=c^{k_1}, \ \dots, \ r_n=c^{k_n}, \ [c,x]=1,\,\forall x \in X \rangle }.\end{equation*}

Suppose $w \in F(X \cup \{c\})$ . Since $c$ is central, $w = \overline{w}c^m$ in $\Gamma$ , for some $m \in \mathbb{Z}$ where $\overline{w}$ is $w$ with all $c^{\pm 1}$ removed. If $w$ represents the identity in $\Gamma$ , the word $\overline{w} \in F(X)$ represents the identity in $\overline{\Gamma }$ . We will describe how to construct a van Kampen diagram for $w$ over $\mathcal{P}_{\Gamma }$ from a diagram $\overline{\Delta }$ for $\overline{w}$ over $\mathcal{P}_{\overline{\Gamma }}$ .

We read a defining relator $r_{i_\sigma }$ clockwise or counterclockwise from an appropriate vertex $\ast _\sigma$ around the boundary of each 2-cell $\sigma$ in $\overline{\Delta }$ . Now “charge” every 2-cell: insert $|k_{i_\sigma }|$ loops at $\ast _{\sigma }$ each labeled with $c$ ’s and oriented in such a way that around the interior of the 2-cell we now read $r_{i_\sigma }c^{-k_{i_\sigma }}$ (to reflect the relation $r_{i_\sigma }=c^{k_{i_\sigma }}$ ), as in Figure 2. If $C\;:\!=\; \max _i |k_i|$ , then at most $C \textrm{Area}(\overline{\Delta })$ such loops labeled by $c$ are introduced by charging.

Figure 2. How “charges” would appear if $r_1=c^2$ and $r_2=c$ .

To discharge, pick a geodesic spanning tree $\mathcal{T}$ in $\overline{\Delta }^{(1)}$ —that is, a maximal tree such that the distance in the tree from any vertex to the base vertex of $\overline{\Delta }$ is the same as its distance in $\overline{\Delta }^{(1)}$ . In [16], for each introduced $c$ -edge, a $c$ -corridor is added which follows $\mathcal{T}$ to the root of the tree. (Figures 4–7 in [16] show how these corridors appear.) Each $c$ -corridor has length bounded above by $\textrm{Diam}(\overline{\Delta })$ . This produces a diagram $\Delta ^{\prime }$ for $\overline{w}c^m$ in $\Gamma$ with area at most $C \textrm{Area}(\overline{\Delta })(\textrm{Diam}(\overline{\Delta })+1)$ .

As $w=\overline{w}c^m$ in $\mathcal{P}_{\Gamma }$ , there is a van Kampen diagram $\theta$ for $wc^{-m}(\overline{w})^{-1}$ over $\mathcal{P}_{\Gamma }$ . Since the arrangement of generators other than $c$ is the same in $w$ and in $\overline{w}c^m$ , $\theta$ can be filled with $c$ -corridors and $\textrm{Area}( wc^{-m}\overline{w}^{-1}) \leq |w|^2$ . To get a diagram $\Delta$ for $w$ , we wrap the diagram $\theta$ around $\Delta ^{\prime }$ as in Figure 3.

Figure 3. Constructing $\Delta$ from $\Delta ^{\prime }$ and $\theta$ .

For example, $G = \langle a, b, c \mid [b,a] = c^2, [c, a]=[c,b]=1 \rangle$ is a central extension of $Q = \langle a, b \mid [a,b]=1 \rangle$ .

Figure 4 shows how a van Kampen diagram over $G$ for the word $w =c^{-6}b^{-3} a^{-3}bc^{-1}b^2c^{-1}a^3c^{-10}$ , beginning with a van Kampen diagram $\overline{\Delta }$ over $Q$ for $\overline{w} =b^{-3} a^{-3}b^3a^3$ .

Figure 4. An example of the electrostatic model in action.

We begin by charging the diagram, that is, adding in $c$ -edges (the yellow loops) to all 2-cells to recover the relations of $G$ . Then we “discharge” the new edges to the boundary, that is, we push the one-sided edges to the boundary by adding in c-corridors along a geodesic spanning tree $\mathcal{T}$ . For each unconnected $c$ -edge, we duplicate the path from its vertex to the base point, in $\mathcal{T}$ , and expand these paths to $c$ -corridors. For example, a path with label $abbb$ will be duplicated to a $c$ -corridor with sides $abbb$ , as $c$ is central. Finally, we add an annular diagram around the outside of the diagram to rearrange the $c$ -edges to the appropriate order, converting the van Kampen diagram $\Delta '$ for $c^{-6}b^{-3}a^{-3}b^3a^3c^{12}$ to a van Kampen diagram $\Delta$ for $w$ .

In this example, the area of $\overline{\Delta }$ is 9, and the diameter of the 1-skeleton of $\overline{\Delta }$ is 6. Each of the $2 \times 9$ new $c$ -edges can be pushed to the boundary with the addition of a $c$ -corridor of length at most 6, along a path in the spanning tree, so the van Kampen diagram $\Delta ^{\prime }$ has area at most $9 + 6 \cdot 2 \cdot 9$ , and rearranging the boundary comes at a further cost to area of at most $|w|^2$ .

This construction leads to the following theorem.

Theorem 4.1 (Gersten–Riley [16], Theorem 6.3). Suppose we have a central extension $1 \to \mathbb{Z} \to \Gamma \to \overline{\Gamma } \to 1$ of a finitely presented group $\overline{\Gamma }$ , and $f,g \;:\;\mathbb{N} \to \mathbb{N}$ are functions such that for every word $\overline{w}$ representing the identity in $\overline{\Gamma }$ , there exists a van Kampen diagram $\overline{\Delta }$ such that $\textrm{Area}(\overline{\Delta })\leq f(|\overline{w}|)$ and the diameter $\textrm{Diam}(\overline{\Delta })$ of the 1-skeleton of $\overline{\Delta }$ is at most $g(|\overline{w}|)$ . Then, the Dehn function of $\Gamma$ , $\delta _G(n)$ is bounded above by a constant times $f(n)(g(n)+1)+n^2$ .

To use Theorem 4.1, we need simultaneous control on both area and diameter of diagrams. This is available in the setting we will be concerned with thanks to the following theorem of Papasoglu. The radius $r(\Delta )$ of a van Kampen diagram $\Delta$ is the minimal $N$ such that for every vertex in $\Delta$ , there is a path of length at most $N$ in the 1-skeleton of $\Delta$ from that vertex to $\partial \Delta$ . Since one can travel between any two vertices by concatenating shortest paths to the boundary with a path part way around the boundary:

(4.1) \begin{equation} \textrm{Diam}(\Delta ) \ \leq \ 2r(\Delta ) + |\partial \Delta |. \end{equation}

Theorem 4.2 (Papasoglu, Section 3 of [22]). For a group $G$ given by a finite presentation in which every relator has length at most three, if $\Delta$ is a minimal area van Kampen diagram such that $|\partial \Delta |= n$ and $\textrm{Area}(\Delta ) \leq M n^2$ , then $r(\Delta ) \leq 12Mn$ .

Every finitely presentable group has such a presentation, and changing between two finite presentations of a group alters diameter and area by at most a multiplicative constant, so, in the light of (4.1), Theorem 4.2 gives us:

Corollary 4.3. If a finitely presented group $G$ has Dehn function bounded above by a quadratic function, then there exists $K\gt 0$ such that for every word of length $n$ representing the identity, there is a van Kampen diagram whose area is at most $Kn^2$ and whose diameter is at most $Kn$ .

5. Mapping tori of $G = F_2 \times \mathbb{Z} = \langle a,b \rangle \times \langle c \rangle$

5.1. Automorphisms of $F_2 \times \mathbb{Z}$

Recall the notation of Theorem A: $\Psi \in{\textrm{Aut}}(F_2 \times \mathbb{Z})$ induces $\psi \in{\textrm{Aut}}(F_2)$ , $\psi$ induces $\psi _{ab} \in \textrm{GL}(2,\mathbb{Z})$ via the abelianization map $F_2 \to \mathbb{Z}^2$ , $g \mapsto g_{ab}$ , and $p\;:\;F_2 \times \mathbb{Z} \to \mathbb{Z} = \langle c \rangle$ is projection onto the second factor. Let $\lambda ^{\pm 1}$ be the (complex) eigenvalues of $\psi _{ab}$ . We will prove Theorem A by separately addressing three comprehensive and mutually exclusive cases.

1. 1. $\left |\lambda \right |\neq 1$ ,

2. 2. $\left |\lambda \right | = 1$ and there exists $g \in F_2$ and $m \in \mathbb{N}$ such that $\psi _{ab}^m(g_{ab}) = g_{ab}$ and $p(\Psi ^m(g)) \neq 0$ —equivalently, $g_{ab} = [\psi ^m(g)]_{ab}$ and $\Psi ^m(g) = \psi ^m(g)c^k$ for some $k \neq 0$ .

3. 3. all other cases—that is, $\left |\lambda \right | = 1$ and for all $g \in F_2$ and all $m \in \mathbb{N}$ , if $p(\Psi ^m(g)) \neq 0$ then $\psi _{ab}^m(g_{ab}) \neq g_{ab}$ .

In Section 5.2, we will prove that the Dehn function of the mapping torus $M_{\Psi }$ of $F_2 \times \mathbb{Z} = \langle a,b \rangle \times \langle c \rangle$ is quadratic in case 1. In Section 5.3, we will prove that it is cubic in case 2 and is quadratic in case 3. First, we narrow the family of automorphisms $\Psi$ that must be explored.

Lemma 5.1 ([20, Proposition 4.1, due to Nielsen]). For all $\,\theta \in{\textrm{Aut}}(F(a,b))$ , there is $h \in F(a,b)$ such that $\theta ^2([a,b])=[a,b]^h$ .

Proof. ${\textrm{Aut}}(F(a,b))$ is generated by the following five elementary Nielsen transformations: $(a,b)$ maps to $(a^{-1}, b)$ , $(a, b^{-1})$ , $(b, a)$ , $(ab, b)$ , or $(a, ba)$ . Each sends $[a,b]$ to a conjugate of $[a,b]^{\pm 1}$ .

To prove Theorem A, it will suffice to focus only on the mapping tori of the form $M_{\Phi }$ described in the next lemma.

Lemma 5.2. Let $G = F_2 \times \mathbb{Z} = \langle a, b \rangle \times \langle c \rangle$ . Given $\Psi \in{\textrm{Aut}}(G)$ , there exists $\Phi \in{\textrm{Aut}}(G)$ such that

• there is $k \geq 0$ such that $[\Phi ] = [\Psi ^k]$ in $\textrm{Out}(F_2\times \mathbb{Z})$ ,

• the Dehn functions of $M_{\Psi }$ and $M_{\Phi }$ are equivalent,

• $\phi ([a,b]) = [a,b]$ ,

• $M_{\Phi }$ is a central extension of $M_{\phi } = \langle a, b, t \mid a^{t}=\phi (a), \ b^{t}=\phi (b) \rangle$ by $\mathbb{Z} = \langle c \rangle$ ,

where $\phi \in{\textrm{Aut}}(F(a,b))$ is the map induced from $\Phi$ by killing $c$ . Thus, there exist $k_a, k_b \in \mathbb{Z}$ such that

\begin{equation*}M_{\Phi } \ = \ \langle a, b, c, t \mid a^{t}=\phi (a)c^{k_a}, \ b^{t}=\phi (b)c^{k_b},\ c^{t}=c, \ [a,c]=1, \ [b,c]=1 \rangle .\end{equation*}

Additionally, by replacing $\Phi$ by $\Phi ^l$ for a suitable $l$ , we can further achieve that the map $\phi _{ab}$ induced by $\phi$ via abelianizing $F(a,b)$ to $\mathbb{Z}^2$ has determinant $1$ and its eigenvalues are real and positive.

Finally, each of conditions 1, 2, and 3 from the start of this section hold for $\Phi$ exactly when they hold for $\Psi$ .

Proof. The center $\langle c \rangle$ of $G$ , being characteristic, is preserved by $\Psi$ , so $\Psi (c) = c^{\pm 1}$ , and $\Psi ^2(c) =c$ . On killing $c$ , $\Psi$ induces some $\psi \in{\textrm{Aut}}(F(a,b))$ , whereby the mapping torus $M_{\Psi ^2} = G \rtimes _{\Psi ^2} \mathbb{Z}$ is

\begin{equation*}\langle a, b,c, t \mid a^{t}=\psi ^2(a)\,c^{k_a}, \ b^{t}=\psi ^2(b)\,c^{k_b},\ c^{t}=c, \ [a,c]=1, \ [b,c]=1\rangle \end{equation*}

for some $k_a, k_b \in \mathbb{Z}$ . By Lemma 5.1, $\psi ^2([a,b]) =[a,b]^h$ for some $h \in F(a,b)$ .

How we will define $\Phi$ will depend on which of the cases 1, 2, and 3 from the start of this section, $\Psi$ falls into, as well as whether $\psi _{ab}$ is finite order or has linear growth.

In case 1, define $\Phi = \iota _{h^{-1}}\circ \Psi ^2$ where $\iota _{h^{-1}}$ denotes conjugation by $h^{-1}$ . Then $\phi _{ab}$ has determinant 1 as $(\psi _{ab})^2$ has determinant 1, and $\Phi$ satisfies the properties above by definition and by Lemma 3.6. Because the eigenvalues of $\psi _{ab}$ were real, the eigenvalues of $\phi _{ab}$ are real and positive.

In cases 2 and 3, $\psi _{ab}$ has unit eigenvalues. If these eigenvalues are not real, Lemma 3.8 tells us that $\psi _{ab}$ has order dividing $6$ . Define $\Phi$ to be $\Psi ^6$ composed with an appropriate inner automorphism so that $\phi = \textrm{id}$ . Otherwise, $\phi _{ab}$ has real eigenvalues of $\pm 1$ . Define $\Phi$ to be $\Psi ^2$ , composed with the inner automorphism guaranteed by Lemma 5.1 so that $\phi ([a,b]) = [a,b]$ . In both cases, $\phi$ and $\Phi$ satisfy all the required properties (again using Lemma 3.6).

Here is why conditions 1, 2, and 3 hold for $\Phi$ exactly when they hold for $\Psi$ . Suppose that $\Psi$ satisfies condition 1, that $\psi _{ab}$ has a non-unit eigenvalue. Then $\Phi = \iota _{h^{-1}}\circ \Psi ^2$ for some $h \in F(a,b)$ , and $\psi _{ab}$ has a non-unit eigenvalue if and only if $\phi _{ab}= \psi ^2_{ab}$ does. Suppose that $\Psi$ satisfies condition 2 or 3, and $\psi _{ab}$ has complex eigenvalues. Then $\Phi = \iota _{h^{-1}}\circ \Psi ^6$ for some $h\in F(a,b)$ . If for some $g \in F(a,b)$ , we have that $g_{ab}$ is a fixed point of $\psi _{ab}^m$ , then it is also a fixed point of $\phi _{ab}^m=\psi _{ab}^{6m}$ . If there is $m\in \mathbb{N}$ so that $\phi _{ab}^m$ has a fixed point, then $\psi _{ab}^{6m}$ will also have a fixed point. Moreover, $p(\Phi ^{m}(g)) = 6p(\Psi ^m(g))$ , so $p(\Phi ^m(g))=0$ if and only if $p(\Psi ^m(g))=0$ . Thus, $\Phi$ and $\Psi$ either both satisfy 2 or both satisfy 3. The real case follows by a similar argument.

We are now ready to deduce:

Corollary 5.3. All mapping tori $M_{\Phi }$ of $F_2 \times \mathbb{Z}$ have at most a cubic Dehn function.

Proof. Bridson and Groves [8] prove that for all $\phi \in{\textrm{Aut}}(F_2)$ , $F_2 \rtimes _{\phi } \mathbb{Z}$ has a quadratic Dehn function, so Corollary 4.3 applies and allows us to use Theorem 4.1 to deduce that every central extension of $F_2 \rtimes _{\phi } \mathbb{Z}$ has at most cubic Dehn function. Lemma 5.2 then tells us that $M_{\Phi }$ has at most a cubic Dehn function.

In Sections 5.2 and 5.3, we will refine this method to improve the upper bound from cubic to quadratic in special cases. In Section 6, we will adapt the arguments to certain examples which fall short of being central extensions.

5.2. Theorem A when $\psi _{ab}$ has non-unit eigenvalues

The primary tool for this section is relative hyperbolicity, a concept introduced by Gromov, and then developed by Bowditch, Farb, Osin, and others [5, 14, 21].

Suppose $M_{\phi }$ is a group presented by:

\begin{equation*}\mathcal {P}_1 \ \;:\!=\; \ \langle a, b, t \mid a^{t}=\phi (a), \ b^{t}=\phi (b) \rangle \end{equation*}

where $\phi \in{\textrm{Aut}}(F(a,b))$ such that $\phi ([a,b]) = [a,b]$ .

Lemma 5.4. If $\phi _{ab}$ has non-unit eigenvalues, $M_{\phi }$ is strongly hyperbolic relative to the subgroup:

\begin{equation*}H\,\;:\!=\;\,\langle [a,b], \ t \rangle \,\cong \,\mathbb {Z}^2.\end{equation*}

Proof. $M_{\phi }$ is the fundamental group of a finite-volume hyperbolic once-punctured torus bundle. In Theorem 4.11 of [14], Farb showed that such groups are strongly hyperbolic relative to their cusp subgroups. In our case, that is the subgroup $\langle [a,b], \ t \rangle$ (see also Section 4 of [12] for a survey of when mapping tori of free groups are relatively hyperbolic and acylindrically hyperbolic).

Consider the presentation:

\begin{equation*}\mathcal {P}_2 \ \;:\!=\; \ \langle a, b, z, t \mid a^{t}=\phi (a), \ b^{t}=\phi (b), \ z=[a,b], \ z^t=z \rangle \end{equation*}

for $M_{\phi }$ obtained from $\mathcal{P}_1$ by adding an extra generator $z$ , an extra relation which declares that $z$ equals $[a,b]$ in the group, and a further extra relation which declares that $[a,b]$ commutes with $t$ (which is a consequence of the other defining relations since $\phi ([a,b]) = [a,b]$ , but we include it nevertheless). Then, $\langle t, z \rangle \cong \mathbb{Z}^2$ is the subgroup $H$ of Lemma 5.4. Refer to faces of a van Kampen diagram over $\mathcal{P}_2$ as $\mathbb{Z}^2$ -faces when they correspond to the relation $z^t=z$ , and refer to the remaining faces as $\mathcal{R}$ -faces.

Lemma 5.5. There exists $C\gt 0$ such that every word $w$ on $\left \{a, b, t\right \}^{\pm 1}$ of length $n$ that represents the identity has a van Kampen diagram $\Delta$ over $\mathcal{P}_2$ with the following properties.

1. 1. The number of $\mathcal{R}$ -faces is at most $Cn$ .

2. 2. The number of $\mathbb{Z}^2$ -faces in $\Delta$ is at most $Cn^2$ .

3. 3. From every vertex of $\Delta$ on the perimeter of an $\mathcal{R}$ -face, there is a path to $\partial \Delta$ of length at most $Cn$ in the 1-skeleton of the union of the $\mathcal{R}$ -faces.

Proof. Let $\mathcal{A}_H=\left \{t,z\right \} \cup \{h_{ij} \mid i,j \in \mathbb{Z}, \ (i,j) \neq (0,0), (1, 0), (0,1) \}$ be an alphabet, with a letter for each non-identity element of the subgroup $\langle t, z \rangle \cong \mathbb{Z}^2$ of $M_{\phi }$ . Here, $h_{ij}$ corresponds to the element represented by $t^{i}z^{j}$ . Let $S$ denote the set of words in $\mathcal{A}_H^{\ast }$ that represent the identity in $M_{\phi }$ . For example, $S$ includes the word $[z,t]$ and $h_{ij}z^{-j}t^{-i}$ for all $(i,j) \neq (0,0), (1, 0), (0,1)$ .

The presentation

\begin{equation*} \mathcal {P}_3 \ \;:\!=\; \ \langle a, b, \mathcal {A}_H \mid a^{t} = \phi (a), \ b^{t} = \phi (b), \ z=[a,b], \ S \rangle \end{equation*}

again gives $M_{\phi }$ . Note that the elements $t$ and $z$ appear in $\mathcal{A}_H$ , and the defining relation $z^t=z$ appears in $S$ . Again, we will refer to van Kampen diagram faces that correspond to elements of $S$ as $\mathbb{Z}^2$ -faces.

Then $\mathcal{P}_3$ is a finite relative presentation for $M_{\phi }$ with respect to the subgroup $H$ , as per Definitions 2.2 and 2.3 of Osin in [21]. Theorem 1.5 in [21] says (in particular) that a finitely generated group which is hyperbolic relative to a subgroup in the sense of Farb, as is the case for $M_{\phi }$ relative to $H$ by Lemma 5.4, has a linear relative Dehn function. What this means (as unpacked per Definitions 2.26, 2.31, and 2.32 of [21]) is that there exists $C\gt 0$ such that for every word $w$ on $\{a,b,t\}^{\pm 1}$ representing the identity, there is a van Kampen diagram $\hat{\Delta }$ over $\mathcal{P}_3$ whose number of $\mathcal{R}$ -faces is at most $C |w|$ .

Osin proves further facts that we will need concerning the geometry of $\hat{\Delta }$ . A diagram for the word $w$ is of minimal type over all diagrams for $w$ if under lexicographic ordering it minimizes

\begin{align*} (N_{\mathcal{R}} = \#\ \text{of}\ \mathcal{R}-\text{faces}, \ \ N_{\mathbb{Z}^2} = \# \ \text{of} \ \mathbb{Z}^2-\text{faces}, \ \ E= \text{total} \# \text{of edges}). \end{align*}

Choose $\hat{\Delta }$ be of minimal type.

Let $M$ be the maximum length of the relators $a^{t}\phi (a)^{-1}$ , $b^{t}\phi (b)^{-1}$ , $z[a,b]^{-1}$ , and $z^tz^{-1}$ . Call an edge of $\hat{\Delta }$ internal to the $\mathbb{Z}^2$ -faces when it has $\mathbb{Z}^2$ -faces (or a $\mathbb{Z}^2$ -face) on both sides. Osin (Lemma 2.15 of [21]) tells us that if $\hat{\Delta }$ is of minimal type then it has no edges which are internal to the $\mathbb{Z}^2$ -faces and deduces (Corollary 2.16) that the sum of the lengths of the perimeters of $\mathbb{Z}^2$ -faces in $\hat{\Delta }$ is at most $|w| + M N_{\mathcal{R}}$ .

Suppose that $w$ is a word on $\{a,b, t\}^{\pm 1}$ and take $\hat{\Delta }$ to be a diagram of minimal type for $w$ over $\mathcal{P}_3$ .

The words around $\mathcal{R}$ -faces only include the letters $t, z, a$ and $b$ , so they can overlap $\mathbb{Z}^2$ -faces only in edges labeled by $t$ and $z$ . Therefore, the word around each $\mathbb{Z}^2$ -face is a word on $\{t, z\}^{\pm 1}$ since every edge in the boundary of a $\mathbb{Z}^2$ -face is either in $\partial \hat{\Delta }$ or is also in the boundary of an $\mathcal{R}$ -face. Let $\Delta$ be a diagram obtained from $\hat{\Delta }$ by excising all $\mathbb{Z}^2$ -faces and replacing each $\mathbb{Z}^2$ -face with the appropriate minimal area diagram over $\langle t, z \mid z^t =z \rangle$ . So $\Delta$ is a van Kampen diagram over $\mathcal{P}_2$ . By Osin’s Theorem 1.5, as discussed above, $\Delta$ satisfies (1). As the Dehn function of $\langle t, z \mid z^t =z \rangle$ enjoys a quadratic upper bound, and, given the bound on the lengths of the boundaries of $\mathbb{Z}^2$ -faces explained in the previous paragraph, $\Delta$ also satisfies (2).

Because of the minimality assumption on the number of $\mathbb{Z}^2$ -faces, no two $\mathbb{Z}^2$ -faces will have a vertex in common in $\hat{\Delta }$ : two $\mathbb{Z}^2$ -faces with a vertex in common could be replaced by a single $\mathbb{Z}^2$ -face. Also the boundary circuit of any $\mathbb{Z}^2$ -face in $\hat{\Delta }$ will be a simple loop. This is because $E(\hat{\Delta })$ is minimal: a $\mathbb{Z}^2$ -face with a non-simple loop as its boundary circuit could be excised and a $\mathbb{Z}^2$ -face with a shorter and simple boundary loop inserted in its place. Thus, the $\mathbb{Z}^2$ -faces form disjoint islands in $\hat{\Delta }$ and there are no $\mathcal{R}$ -faces enclosed within these islands. In the light of this, (3) follows from (1).

Proof of Theorem A in Case 1. We suppose $\Psi \in{\textrm{Aut}}(F_2 \times \mathbb{Z})$ . By Lemma 5.2, there exists $\Phi$ so that $M_{\Phi }$ and $M_{\Psi }$ have equivalent Dehn function, and $M_{\Phi }$ has presentation:

\begin{equation*}\langle a, b,c, t \mid a^{t}=\phi (a)c^{k_a}, \ b^{t}=\phi (b)c^{k_b},\ c^{t}=c, \ [a,c]=1, \ [b,c]=1\rangle,\end{equation*}

which is a central extension of

\begin{equation*} \langle a, b, t \mid a^{t}=\phi (a), \ b^{t}=\phi (b) \rangle \end{equation*}

where $\phi \in{\textrm{Aut}}(F(a,b))$ has the property that $\phi ([a,b]) = [a,b]$ . If $z = [a,b]$ , then in $M_{\Phi }$

\begin{equation*}z^t \ = \ [a^t,b^t] \ = \ [\Phi (a),\Phi (b)] \ = \ [\phi (a)c^{k_a}, \phi (b)c^{k_b}] \ = \ [\phi (a), \phi (b)] \ = \ \phi ([a,b]) \ = \ [a,b] \ = \ z.\end{equation*}

So $M_{\Phi }$ also can be presented as:

\begin{equation*}\mathcal {Q} \ \;:\!=\; \ \langle a, b,c, t, z \mid a^{t}=\phi (a)c^{k_a}, \ b^{t}=\phi (b)c^{k_b},\ c^{t}=c, \ [a,c]=1, \ [b,c]=1, \ z = [a,b], \ z^t=z \rangle,\end{equation*}

which reveals it to be a central extension of

\begin{equation*} \mathcal {P}_2 \ = \ \langle a, b, t, z \mid a^{t}=\phi (a), \ b^{t}=\phi (b), \ z=[a,b], \ z^t =z \rangle \end{equation*}

by $\mathbb{Z} = \langle c \rangle$ .

Suppose $w$ is a word in $\{a,b, c, t\}^{\pm 1}$ of length $n$ representing the identity in $\mathcal{Q}$ . Let $\overline{w}$ be $w$ with all $c^{\pm 1}$ deleted.

Let $\overline{\Delta }$ be a van Kampen diagram for $\overline{w}$ as per Lemma 5.5. Given (3) of that lemma, there is a forest $\mathcal{F}$ in the 1-skeleton of the union of the $\mathcal{R}$ -faces in $\overline{\Delta }$ joining every vertex of an $\mathcal{R}$ -face to $\partial \overline{\Delta }$ by a path of length at most $Cn$ .

Charge $\overline{\Delta }$ . Given that the defining relation $z^t =z$ is unchanged on lifting to the central extension, the $\mathbb{Z}^2$ -faces of Lemma 5.5 (2) are unchanged. There are $Cn^2$ such $\mathbb{Z}^2$ faces. Let $m = \max \{|k_a|, |k_b|\}$ . The remaining $Cn$ $\mathcal{R}$ -faces of Lemma 5.5 (1) each acquire at most $m$ charges. These are discharged by adding partial $c$ -corridors that follow the forest $\mathcal{F}$ to the boundary and then around the boundary to a base vertex. Each partial $c$ -corridor has length at most $(C+1)n$ : the length of the path to the boundary is at most $Cn$ by Lemma 5.5 (3) and the length of the path to the base vertex is at most $n$ . In total then, $c$ -partial corridors contribute at most $(C+1)^{2}mn^2$ 2-cells to the new diagram. The result is a diagram over $\mathcal{Q}$ of area at most $((C+1)^{2}m +C) n^2$ for a word $\overline{w}c^k$ , which has length less than $n$ . By adding in an annular region to rearrange $\overline{w}c^k$ to $w$ , as per the electrostatic model of Section 4, it follows that $w$ has a diagram over $\mathcal{Q}$ of area at most $({(C+1)}^{2}m +C+1) n^2$ .

5.3. Theorem A in the case where all eigenvalues of $\psi_{\boldsymbol{ab}}$ are unit

We begin by arguing that for the purpose of determining Dehn functions, we can further specialize the family of presentations as follows.

Lemma 5.6. Suppose that $\Phi \in{\textrm{Aut}}(G)$ is as per Lemma 5.2, and that eigenvalues of $\phi _{ab}$ are $1$ . Then there exists $\Xi \in{\textrm{Aut}}(G)$ such that the eigenvalues of $\xi _{ab}$ are also $1$ , the Dehn functions of $M_{\Phi }$ and $M_{\Xi }$ are equivalent, and

\begin{equation*}M_{\Xi }=\langle a, b, c, t \mid a^t=ab^{\beta }c^{k_a}, b^t= bc^{k_b}, c^t =c, \ [a,c]=1, \ [b,c]=1\rangle \end{equation*}

for some $\beta \in \mathbb{Z}$ . Moreover, conditions 2 and 3 of Section 5.1 hold for $\Psi$ exactly when they hold for $\Xi$ , and they are characterized by $k_b \neq 0$ and $k_b = 0$ , respectively.

Proof. We have $\Phi$ per Lemma 5.2. So $\Phi (a) = \phi (a)c^{k_a'}, \ \Phi (b) = \phi (b)c^{k_b'}, \ \Phi (c) =c$ , for some $k_a', k_b' \in \mathbb{Z}$ and some $\phi \in{\textrm{Aut}}(F(a,b))$ such that $\phi _{ab}$ has determinant $1$ . Lemma 5.2 implied that the eigenvalues of $\phi _{ab}$ are 1 for automorphisms of types 2 and 3.

We will show that there is $\Xi \in{\textrm{Aut}}(F_2 \times \mathbb{Z})$ such that for some $\kappa \geq 0$ , $[\Phi ^\kappa ]$ and $[\Xi ]$ are conjugate in $\textrm{Out}(F_2 \times \mathbb{Z})$ and $\xi = \Xi \!\! \upharpoonright _{F(a,b)}$ maps $b \mapsto b$ .

As $\phi _{ab}$ has only eigenvalue 1, it is either the identity or it has linear growth. Lemma 3.7, implies that for some $\kappa$ , $\phi ^\kappa _{ab}$ is conjugate in $\textrm{SL}(2, \mathbb{Z})$ to $\left (\begin{smallmatrix} 1 & \beta \\[5pt] 0 & 1 \end{smallmatrix}\right )$ for some $\beta \in \mathbb{Z}$ . Define $\Phi ^\prime =\Phi ^\kappa$ , with restriction $\phi ^\prime$ . On account of the standard isomorphism between $\textrm{Out}(F_2)$ and $\textrm{GL}(2,\mathbb{Z})$ , $[\phi ^\prime ]$ is conjugate in $\textrm{Out}(F_2)$ to $[\xi ]$ where $\xi (a) = ab^{\beta }$ and $\xi (b) = b$ . So $\xi = f^{-1}\circ \phi ^\prime \circ f\circ \iota _g$ for some $f \in{\textrm{Aut}}(F_2)$ and some $\iota _g \in \textrm{Inn}(F_2)$ . We lift $f, \xi, \iota _g \in{\textrm{Aut}}(F_2)$ to $F, \Xi, \hat{\iota }_g \in{\textrm{Aut}}(F_2 \times \mathbb{Z})$ by defining $F(gc^k) = f(g)c^k$ for $g \in F_2$ and $k \in \mathbb{Z}$ , by taking $\hat{\iota }_g$ to be conjugation by $g$ , and by defining $\Xi \;:\!=\; F^{-1} \circ \Phi ^\prime \circ F \circ \hat{\iota }_g$ . Because $c$ is central, $\hat{\iota }_g(c) = c$ . In particular,

\begin{equation*}\Xi \;:\; a \mapsto ab^{\beta }c^{k_a}, \ \ b \mapsto bc^{k_b}, \ \ c \mapsto c,\end{equation*}

for some $k_a, k_b \in \mathbb{Z}$ . (Note that $p( \Phi ^{\prime }(b))$ and $p(\Xi (b)) = k_b$ may not be equal, as $\Phi ^\prime (f(b)^{g^{-1}})$ , and $\Phi ^\prime (b)$ will not generally have the same index sum of $c$ letters.)

Therefore, $M_{\Xi }$ has the presentation claimed and $\xi _{ab}$ has only $1$ as an eigenvalue, as required. By Lemma 3.6, the mapping tori $M_{\Phi }$ and $M_{\Xi }$ have equivalent Dehn functions.

Next we will show that

1. 1. If $\phi ^{\prime }_{ab} \neq \textrm{id}$ , then $p(\Xi (b))=k_b\neq 0$ if and only if there exists $w \in F_2$ such that $\phi ^{\prime }_{ab}(w_{ab})= w_{ab}$ and $p(\Phi ^{\prime }(w)) \neq 0$ .

2. 2. If $\phi ^{\prime }_{ab} = \textrm{id}$ , exactly one of the following holds:

   1. (a) $p(\Phi ^\prime (x)) = 0$ for all $x \in \langle a,b \rangle$ , in which case $\Xi =\textrm{Id}$ ,

   2. (b) $p(\Phi ^\prime (x)) \neq 0$ for some $x$ , in which case $p(\Xi (a))$ or $p(\Xi (b))$ is nonzero.

Moreover, this implies that $\Phi$ , $\Phi '$ and $\Xi$ either all satisfy condition 2 or all satisfy condition 3 of Section 5.1.

Proof of 1: We wish to compare $p(\Phi ^\prime (w))$ and $p(\Xi (b))$ . Let $w^{\prime } = f(b)$ . The following calculation shows that $w_{ab}^{\prime }$ is another fixed point of $\phi ^\prime _{ab}$ and that $p(\Phi ^\prime (w^{\prime })) =p(\Xi (b))= k_b$ :

\begin{equation*}\Phi ^\prime (w^{\prime }) \ = \ F\circ \Xi \circ \iota _{g^{-1}}\circ F^{-1}(f(b)) \ = \ F(\Xi (b^{g^{-1}})) \ = \ F(b^{g^{-1}}c^{p(\Xi (b))}) \ = \ f(b)^{g^{-1}}c^{p(\Xi (b))} \ = \ (w')^{g^{-1}}c^{p(\Xi (b))}.\end{equation*}

If $\phi ^{\prime }_{ab} \neq \mbox{id}$ , then since $w_{ab}$ and $w^{\prime }_{ab}$ are both fixed by $\phi ^{\prime }_{ab}$ , $w_{ab} = dw^{\prime }_{ab}$ for some $d\neq 0$ , and therefore $p(\Phi ^{\prime }(w)) = dp(\Phi ^{\prime }(w^{\prime })) = dk_b$ . So $p(\Xi (b))=k_b\neq 0$ if and only if $p(\Phi ^{\prime }(w)) \neq 0$ . In case 1, $\Phi ^{\prime }$ and $\Xi$ either both satisfy condition 2 or both satisfy condition 3, and so this holds for $\Psi$ and $\Xi$ by Lemma 5.2.

Proof of 2: $\phi ^{\prime } \in \textrm{Inn}(F_2)$ since

\begin{equation*}1\to \textrm {Inn}(F_2) \to {\textrm {Aut}}(F_2) \to \textrm {SL}(2,\mathbb {Z})\to 1\end{equation*}

is exact and $\phi ^{\prime }_{ab}=\textrm{id}$ . Therefore, $\Xi$ maps $a \mapsto ac^{k_a}$ , $b \mapsto bc^{k_b}$ , and $c \mapsto c$ for some $k_a, k_b \in \mathbb{Z}$ , and so $\xi _{ab} = \mbox{id}$ also. This suffices to show 2.

When $\phi ^{\prime }_{ab}= \mbox{id}$ , condition 2 amounts to “there exists $g \in F_2$ such that $p(\Phi ^{\prime }(g)) \neq 0$ ”. This holds for $\Phi ^{\prime }$ if and only if it holds for $\Xi$ , by 2. Again $\Phi$ , $\Phi '$ and $\Xi$ either all satisfy condition 2 or all satisfy condition 3, and so this holds for $\Psi$ and $\Xi$ by Lemma 5.2.

Proof of Theorem A in Case 2. By Lemmas 5.2 and 5.6, for the purpose of calculating the Dehn function we may work with

\begin{equation*}M_{\Xi }=\langle a, b, c, t \,|\, a^t=ab^{\beta }c^{k_a},\, b^t= bc^{k_b},\, c^t =c, \ [a,c]=1, [b,c]=1\rangle \end{equation*}

where $k_b \neq 0$ . The subgroup $K \;:\!=\; \langle b, c \mid [b,c] \rangle \cong \mathbb{Z}^2$ quasi-isometrically embeds in $F_2 \times \langle c \rangle$ and $\Xi (K) = \langle bc^{k_b}, c \rangle = K$ . So, by Lemma 3.5, $n \mapsto n^2 \max \{|\Xi ^n(b)|, |\Xi ^n(c)|\}= n^2(k_bn+1)$ is a lower bound for the Dehn function of $M_{\Xi }$ . This lower bound is cubic (as $k_b \neq 0$ ), matching our upper bound from Corollary 5.3, so the claim is established.

We now turn to case 3. This time, Lemmas 5.2 and 5.6 allow us to work with $M_{\Xi }$ which has the form:

\begin{equation*}M_{\Xi }=\langle a, b, c, t \,|\, a^t=ab^{\beta }c^{k_a}, \,b^t= b,\, c^t =c, \ [a,c]=1, [b,c]=1\rangle \end{equation*}

where, $\beta$ is nonzero. (The case $\beta =0$ and $k_a \neq 0$ is covered by Theorem A in case 2—the Dehn function of this mapping torus is cubic. If $\beta =0$ and $k_a =0$ , then $M_{\Xi } = \langle a, b, c \mid [a,c]=1, [b,c]=1 \rangle \times \langle t \rangle$ , which has quadratic Dehn function.)

The methods of case 1 cannot be used here. Indeed, Button and R. Kropholler in Theorem 4.4 [12] have shown that for $\xi$ with this form, $M_{\xi }$ is not strongly hyperbolic relative to any finitely generated proper subgroup, so van Kampen diagrams over $M_{\xi }$ do not decompose into uncharged islands with linear-area complement. Instead will use a variant of the electrostatic model whereby the diagram will be discharged along partial corridors (see Section 3.1) in a manner controlled by an application of Hall’s Marriage Theorem, which we now review.

A subgraph $F$ of a graph $\Gamma$ is a 1-factor for $\Gamma$ if it contains all vertices of $\Gamma$ and each vertex meets precisely one edge of $F$ . In other words, a 1-factor pairs every vertex with a neighbor. We will be interested in the following special case:

Lemma 5.7. A $k$ -regular bipartite graph $\Gamma$ with $k\geq 1$ has a 1-factor.

This is a consequence of Hall’s Marriage Theorem. See [13] for a proof.

Proof of Theorem A in Case 3. By Lemma 5.6, it suffices to prove that $M_{\Phi }$ , presented by:

\begin{equation*}\mathcal {P}= \langle a, b, t, c \mid a^t=ab^{\beta }c^{k_a}, \ b^t=b,\ ac=ca,\ bc=cb, \ ct=tc \rangle,\end{equation*}

has quadratic Dehn function. If $k_a =0$ , then $M_{\Phi }\cong M_{\phi }\times \langle c \rangle$ and so the Dehn functions of $M_{\Phi }$ and $M_{\phi }$ agree and are quadratic. Therefore, we may restrict our attention to the case where $\beta$ and $k_a$ are both nonzero.

Van Kampen diagrams over $\mathcal{P}$ have both partial $b$ -corridors and partial $c$ -corridors. $M_{\Phi }$ is a central extension of $M_{\phi }$ by $\langle c \rangle$ , where $M_{\phi }$ is presented by:

\begin{equation*}\mathcal {Q} \ = \ \langle a, b, t \mid a^t=ab^{\beta }, b^t=b \rangle .\end{equation*}

Van Kampen diagrams over $\mathcal{Q}$ may have partial $b$ -corridors.

Suppose $w$ is a word of length $n$ representing the identity in $\mathcal{P}$ . Let $\overline{w}$ be $w$ with all $c^{\pm 1}$ removed. Then $w = \overline{w}c^m$ in $M_{\Phi }$ for some $m \in \mathbb{Z}$ and $|\overline{w}| \leq |w|$ . Since $\mathcal{Q}$ is free-by-cyclic and non-hyperbolic, it has a quadratic Dehn function. So there exists a minimal area diagram $\overline{\Delta }$ for $\overline{w}$ over $\mathcal{Q}$ such that $\textrm{Area}(\overline{\Delta }) \leq C |\overline{w}|^2$ . We charge $\overline{\Delta }$ by replacing 2-cells in $\overline{\Delta }$ with 2-cells labeled by the defining relators from $\mathcal{P}$ , as in the first steps of the electrostatic model (see Section 4). What follows is a scheme for adding in 2-cells to “discharge” $\overline{\Delta }$ so as to create a diagram for $\overline{w}c^m$ over $\mathcal{P}$ .

The idea is that if we can pair off oppositely oriented capping faces that are joined by partial $b$ -corridors, then we can add in partial $c$ -corridors following the $b$ -corridors, as in Figure 5, in order to discharge the $c$ -edges in our diagram. As $c$ is central in $\mathcal{P}$ , partial $c$ -corridors can be run alongside this partial $b$ -corridor, and the word one reads along both the top and bottom of the $c$ -corridor will be the same as that word along the top and bottom of the $b$ -corridor, namely some power of $t$ . We wish to find a consistent way of partnering vertices so that we can replicate the picture in Figure 5, adding in partial $c$ -corridors to discharge between partners throughout the van Kampen diagram, with no leftover charges to consider.

Figure 5. If a partial $b$ -corridor joins two capping faces in $\overline{\Delta }$ , their $c$ -charges can be discharged by adding partial $c$ -corridors “following” that partial $b$ -corridor.

I. Modeling $\overline{\Delta }$ with a graph. Construct a planar graph with multi-edges, $\Gamma$ , from $\overline{\Delta }$ as illustrated in Figure 6: $\Gamma$ has a black vertex for each capping face in $\overline{\Delta }$ ; whenever two capping faces are connected by a partial $b$ -corridor, possibly of length zero, an edge connects the corresponding vertices (two vertices may share multiple edges); we also add an edge and a white vertex to $\Gamma$ for each partial $b$ -corridor that goes to the boundary. Every black vertex in the graph $\Gamma$ is degree $|\beta |$ and every white vertex has degree 1.

Figure 6. From capping faces and partial corridors in $\overline{\Delta }$ , construct a graph $\Gamma$ . Black vertices correspond to capping faces, white vertices correspond to 1-cells labeled $b$ in $\partial \overline{\Delta }$ , and the edges correspond to partial $b$ -corridor.

The graph $\Gamma$ is bipartite (but not generally black–white bipartite, as you can see in Figure 6): partition the black vertices according to whether they correspond to capping faces with clockwise or anticlockwise oriented $b$ -edges and extend this partition to the white vertices.

II. Building a regular bipartite graph. We would like to apply Lemma 5.7, but $\Gamma$ may not be regular: black vertices have degree $\left |\beta \right |$ , but white vertices have degree $1$ . So, as illustrated in Figure 7a, we construct a regular graph $\hat{\Gamma }$ which has $\Gamma$ as a subgraph. Take $|\beta |$ many copies of $\Gamma$ , and identify the white vertices in each of the copies. That is,

\begin{equation*}\hat {\Gamma } \ \;:\!=\; \ \displaystyle \left (\bigsqcup _{i=1}^{|\beta |} \Gamma \times \{i\}\right )/ \sim,\end{equation*}

where $(v,i) \sim (v,j)$ for all $i,j$ when $v$ is a white vertex. White vertices are degree one, so the identification of $|\beta |$ copies of $\Gamma$ forces $\hat{\Gamma }$ to be a $|\beta |$ -regular graph. If $\Gamma$ is bipartite with respect to a partition $A \sqcup B$ of its vertices, then $\hat{\Gamma }$ is bipartite with respect to

\begin{equation*}\left ( \bigcup _{i=1}^{|\beta |}A \times \left \{i\right \} \right )/ \sim \ \bigsqcup \ \left ( \bigcup _{i=1}^{|\beta |}B \times \left \{i\right \} \right )/ \sim .\end{equation*}

Figure 7. Finding neighbor partners for $\Gamma$ via Hall’s Marriage Theorem.

III. Finding pairing partners for $b$ - and $c$ -corridors. Lemma 5.7 tells us that $\hat{\Gamma }$ has a 1-factor. This partners each vertex $v \in \hat{\Gamma }$ with an adjacent vertex $v^{\prime }$ . View the image of $\Gamma \times \{1\}$ in $\hat{\Gamma }$ as $\Gamma$ , sitting as a subgraph in $\hat{\Gamma }$ . In the example of Figure 7c, $\Gamma$ is the gray subgraph at the back. If $v \in \Gamma$ is a black vertex, its partner $v'$ is also a vertex of $\Gamma$ , but this may fail for white vertices.

IV. Completing to a van Kampen diagram. If $v$ and $v^{\prime }$ are partnered black vertices in $\Gamma$ , then the corresponding capping faces are connected by at least one partial $b$ -corridor (possibly of length zero). In $\overline{\Delta }$ , the capping faces $f$ and $f'$ corresponding to $v$ and $v^{\prime }$ have $|k_a|$ many oppositely oriented charges. We will connect these charges with $|k_a|$ partial $c$ -corridors, as in Figure 5. Choose one of the partial $b$ -corridors joining $f$ to $f'$ (there is at least one). Run all of the partial $c$ -corridors for one capping face alongside the partial $b$ -corridor. If a black vertex $v$ is paired with a white vertex $v'$ in $\Gamma$ , run all of the partial $c$ -corridors alongside the partial $b$ -corridor to the boundary. Two white vertices will never be paired. At the ends of partial $b$ -corridors on capping faces, it may be necessary to insert rectangles in which the $b$ -and $c$ -corridors cross, as in Figure 8, but this requires no more than $|\beta ||k_a|\textrm{Area}(\overline{\Delta })$ additional 2-cells. The total number of 2-cells added to $\overline{\Delta }$ in this process is no more than $(|\beta |+1)|k_a|\textrm{Area}(\overline{\Delta })$ .

Figure 8. Partnering in $\Gamma$ gives a consistent way to discharge $c$ -charges.

V. Correcting the boundary. Partial $c$ -corridors follow partial $b$ -corridors to the boundary in groups of $|k_a|$ . The new diagram has boundary length between $|\overline{w}|$ and $(|k_a|+1)|\overline{w}|$ and is a van Kampen diagram over $\mathcal{P}$ for some word $w^{\prime }$ in the pre-image of $\overline{w}$ . Deleting all $c^{\pm 1}$ from $w^{\prime }$ produces $\overline{w}$ , but the arrangement of the $c^{\pm 1}$ letters in $w^{\prime }$ may differ from that in $w$ . As was described in Section 4, we glue around the outside of this diagram an annular diagram with the word $w^{\prime }$ along the inner boundary component and the word $w$ along the outer boundary component. Together, they form $\Delta$ , a van Kampen diagram for $w$ over $\mathcal{P}$ . This annular diagram has area at most $(|k_a|+1)^2|\overline{w}|^2$ , and summing our area estimates, $\Delta$ has area no more than $(1+ (|\beta |+1)|k_a|)\textrm{Area}(\overline{\Delta }) + (|k_a|+1)^2|\overline{w}|^2$ . Since $\textrm{Area}(\overline{\Delta }) \leq C|\overline{w}|^2$ , it follows that there is constant $A\gt 0$ such that for any given word $w$ in the generators of $\mathcal{P}$ that represents the identity, this construction produces a van Kampen diagram of area at most $A|w|^2$ .

6. Mapping tori of $G = \mathbb{Z}^2 \ast \mathbb{Z}= \langle a, b \mid [a,b] \rangle \ast \langle c \rangle$

6.1. Automorphisms of $\mathbb{Z}^2 \ast \mathbb{Z}$

Servatius [24] and Laurence [18] found a generating set for the automorphism group of a RAAG $A(\Gamma )$ based on the underlying graph $\Gamma$ (see Lemma 7.2). For

\begin{equation*}\mathbb {Z}^2 \ast \mathbb {Z} \ = \ \langle a, b \mid [a,b] \rangle \ast \langle c \rangle,\end{equation*}

it consists of the inner automorphisms, inversions, the one nontrivial graph isomorphism ( $a \mapsto b$ , $b \mapsto a$ , and $c \mapsto c$ ), and the four transvections

\begin{equation*}\begin {array}{l@{\quad}l@{\quad}l@{\quad}l} \tau _a \;:\;& a \mapsto ab, & b \mapsto b, & c \mapsto c, \\[5pt] \tau _b \;:\;& a \mapsto a, & b \mapsto ba, & c \mapsto c, \\[5pt] \psi _a \;:\;& a \mapsto a, & b \mapsto b, & c \mapsto ca, \\[5pt] \psi _b \;:\;& a \mapsto a, & b \mapsto b, & c \mapsto cb. \end {array}\end{equation*}

The following lemma and proposition are steps toward Theorem B in that they let us focus on particular presentations for the purposes of classifying Dehn functions of mapping tori of $\mathbb{Z}^2 \ast \mathbb{Z}$ . Recall that $\iota _h$ denotes the inner automorphism $x \mapsto h^{-1} x h$ .

Lemma 6.1. For all $\Psi \in{\textrm{Aut}}( \mathbb{Z}^2 \ast \mathbb{Z})$ , there exist $\Phi \in{\textrm{Aut}}( \mathbb{Z}^2 \ast \mathbb{Z})$ , $\phi \in{\textrm{Aut}}(\mathbb{Z}^2)$ , and words $w$ and $x$ on $a$ and $b$ such that

\begin{equation*}\Phi \;:\; a \mapsto \phi (a), \ \ b \mapsto \phi (b), \ \ c \mapsto wc^{\pm 1}x\end{equation*}

and $[\Phi ] = [\Psi ]$ in $\textrm{Out}(\mathbb{Z}^2 \ast \mathbb{Z})$ . Explicitly, if $\Psi (a) = u_1c^{\epsilon _1}\dots u_n c^{\epsilon _n}u_{n+1}$ , where each $\epsilon _i \neq 0$ and each $u_i \in \langle a, b\rangle$ , and $u_2, \ldots, u_n \neq 1$ , then $n=2m$ is even and for $g \;:\!=\; c^{\epsilon _{m+1}}u_{m+2}\dots u_{2m} c^{\epsilon _{2m}}u_{2m+1}$ , the map $\iota _{g^{-1}}\circ \Psi$ satisfies the properties required of $\Phi$ .

Moreover, $M_{\Psi }$ and $M_{\Phi }$ have equivalent Dehn functions for any such $\Phi$ .

Proof. Since $\textrm{Inn}(\mathbb{Z}^2 \ast \mathbb{Z}) \trianglelefteq{\textrm{Aut}}(\mathbb{Z}^2 \ast \mathbb{Z})$ , all automorphisms $\Psi \in{\textrm{Aut}}(\mathbb{Z}^2 \ast \mathbb{Z})$ can be written as $\iota _h \circ \Phi$ where $\iota _h$ denotes conjugation by some $h \in \mathbb{Z}^2 \ast \mathbb{Z}$ and $\Phi$ is some product of the inversions, transvections, and graph isomorphisms in the generating set above. These inversions, transvections, and graph isomorphisms restrict to automorphisms of the subgroup $\langle a, b \mid [a,b] \rangle$ and map the subset $\langle a, b \rangle c^{\pm 1} \langle a, b \rangle$ to itself. So

\begin{equation*}\Phi \;:\;a \mapsto \phi (a), \ \ b \mapsto \phi (b), \ \ c \mapsto wc^{\pm 1}x,\end{equation*}

for some $\phi \in{\textrm{Aut}}(\mathbb{Z}^2)$ and some words $w$ and $x$ on $a^{\pm 1}$ and $b^{\pm 1}$ . This proves the existence of a $\Phi$ with the required properties. We turn next to how to find such a $\Phi$ explicitly.

Suppose $\Psi (a)$ is as per the statement. For $h \in \mathbb{Z}^2 \ast \mathbb{Z}$ as above, we have that $\Psi (a) \in \iota _{h}( \langle a, b \rangle )$ . So

\begin{equation*} \Psi (a) \ = \ u_1c^{\epsilon _1}\dots u_n c^{\epsilon _n}u_{n+1} \ \in \ h^{-1} \langle a, b \rangle h.\end{equation*}

But, given the free product structure of $\mathbb{Z}^2 \ast \mathbb{Z}$ , that implies that $n=2m$ is even and

\begin{equation*}h \ = \ v c^{\epsilon _{m+1}}u_{m+2}c^{\epsilon _{m+2}}\cdots u_{2m}c^{\epsilon _{2m}}u_{2m+1} \ = \ vg\end{equation*}

where $v$ is some element of $\langle a, b \rangle$ and $g$ is as defined in the statement.

It follows then that $\iota _{g^{-1}} \circ \Psi = \iota _{v} \circ \iota _{h^{-1}} \circ \Psi = \iota _{v} \circ \Phi$ and maps $a \mapsto \phi '(a), \ \ b \mapsto \phi '(b), \ \ c \mapsto w'c^{\pm 1}x'$ for some $\phi ' \in{\textrm{Aut}}(\mathbb{Z}^2)$ and some words $w'$ and $x'$ on $a^{\pm 1}$ and $b^{\pm 1}$ .

By Lemma 3.6, $M_{\Psi }$ and $M_{\Phi }$ have equivalent Dehn functions.

Proposition 6.2. Given $\Phi$ as per Lemma 6.1, there exist $\,\Xi \in{\textrm{Aut}}( \mathbb{Z}^2 \ast \mathbb{Z})$ , $\xi \in{\textrm{Aut}}(\mathbb{Z}^2)$ , and $z \in \langle a, b \rangle$ such that

\begin{equation*}\Xi \;:\; a \mapsto \xi (a), \ \ b \mapsto \xi (b), \ \ c \mapsto cz\end{equation*}

and $M_{\Phi }$ and $M_{\Xi }$ have equivalent Dehn functions. Moreover, Conditions 1, 2, and 3 of Theorem B apply to $\Xi$ exactly when they apply to $\Phi$ . Additionally,

• when $\xi$ has finite order (Condition 1 of Theorem B), we may further assume $\xi \;:\;a \mapsto a, \ b \mapsto b$ , so that

  \begin{equation*}M_{\Xi } \ = \ \langle a,b,c,t \ \mid \ [a,b]=[a,t]=[b,t]=1, \ c^t=ca^kb^l \rangle,\end{equation*}

• when $\xi$ is of infinite order and has only unit eigenvalues (Condition 3 of Theorem B), we may further assume $\xi \;:\;a \mapsto ab^k, \ b \mapsto b$ for some $k \neq 0$ , so that for some $l,m \in \mathbb{Z}$ ,

  \begin{equation*} M_{\Xi } \ = \ \langle a, b,c, t \mid [a,b]=1, \ a^{t}=ab^{k}, \ b^{t}=b,\ c^{t}=c a^lb^m \rangle .\end{equation*}

Proof. How we will define $\Xi$ will depend on the form of $\Phi (c)$ . Recall $\Phi (c)= wc^{\pm 1}x$ as per Lemma 6.1. Define $\Xi _1 \;:\!=\; \iota _{w} \circ \Phi$ and $\Xi _2 \;:\!=\; \iota _{\phi (w)x^{-1}}\circ \Phi ^2$ . If $\Phi (c) = wcx$ , then $\Xi _1(c) = \iota _w \circ \Phi (c) =cz$ where $z=xw$ . If $\Phi (c) = wc^{-1}x$ , then $\Xi _2(c) = \iota _{\phi (w)x^{-1}} \circ \Phi ^2(c) = cz$ where $z=w^{-1}\phi (xw)x^{-1}$ . For $i=1,2$ , let $\xi _i \;:\!=\; \Xi _i \left |_{\langle a, b \rangle } \right .$ , the restriction of $ \Xi _i$ to the $\mathbb{Z}^2$ factor.

Suppose $\xi _i$ has exponential growth (so has a non-unit eigenvalue as per Lemma 3.9 and Condition 2 of Theorem B). Define $\Xi \;:\!=\;\Xi _i$ . Then $\Xi$ has the general form claimed in the proposition, and since $[\Xi _1] = [\Phi ]$ and $[\Xi _2] = [\Phi ]^2$ , Lemma 3.6 implies that $M_{\Phi }$ and $M_{\Xi }$ have equivalent Dehn functions.

Suppose $\xi _i \in{\textrm{Aut}}(\mathbb{Z}^2)$ has finite order $n$ (i.e. $\xi _i$ has trivial growth). Define $\Xi = \Xi _i^n$ . This has the promised form: its restriction to $\langle a,b \rangle$ is the identity and $\Xi (c) = cz$ for some $z \in \langle a,b \rangle$ . Lemma 3.6 implies that $M_{\Xi }$ and $M_{\Phi }$ have equivalent Dehn functions.

Finally, suppose $\xi _i$ is of infinite order and has only unit eigenvalues. Lemma 3.7 implies that for some power $n$ , $(\xi _i)^{n}$ is conjugate in ${\textrm{Aut}}(\mathbb{Z}^2)$ to the automorphism $\xi \;:\;a \mapsto ab^{k}$ , $b \mapsto b$ , for some $k \neq 0$ . Therefore, for some $f \in{\textrm{Aut}}(\mathbb{Z}^2)$ , ${\xi } = f^{-1}\circ{(\xi _i)}^n \circ f$ . Let $F$ be the automorphism that restricts to $f$ on $\mathbb{Z}^2$ and maps $c \mapsto c$ . Define $\Xi \;:\!=\; F^{-1}\circ (\Xi _i)^n \circ F$ . By Lemma 3.6, $M_{\Phi }$ and $M_{\Xi }$ have equivalent Dehn functions. Let $z^{\prime } = z\xi _i(z) \dots (\xi _i)^{n-1}(z)$ and $z^{\prime \prime } = f^{-1}(z^{\prime })$ . Both are elements of $\langle a,b \rangle$ . The map $\Xi$ has the desired form:

\begin{equation*}\Xi (c) = F^{-1} \circ (\Xi _i)^n \circ F(c) = F^{-1} \circ (\Xi _i)^n(c) = F^{-1}(cz^{\prime })= F^{-1}(c) F^{-1}(z^{\prime })=cf^{-1}(z^{\prime })=cz^{\prime \prime }.\end{equation*}

In every case, conditions (1), (2), and (3) of Theorem B apply to $\Xi$ exactly when they apply to $\Phi$ . After all, in each case, the restriction $\xi$ of $\Xi$ to the $\mathbb{Z}^2$ factor is a conjugate of a power of the restriction $\phi$ of $\Phi$ . Let $A$ be the Jordan Canonical Form (JCF) of $\phi$ . For all $k \in \mathbb{N}$ , $A$ is finite order if and only if $A^k$ is finite order, and $A$ has a non-unit eigenvalue if and only if $A^k$ has one too. The JCF is invariant under conjugation.

6.2. Corridors

In each instance of Proposition 6.2,

\begin{equation*}M_{\Xi } \ = \ \langle a, b, c, t \mid [a,b]=1, \ a^t= \xi (a), \ b^t= \xi (b), \ c^t=cz \rangle \end{equation*}

for some $\xi \in{\textrm{Aut}}(\mathbb{Z}^2)$ and some $z \in \langle a,b \rangle$ . In this section, we prove some preliminary results about van Kampen diagrams over this presentation. Such diagrams can have both $c$ - and $t$ -corridors.

Definition 6.3. Suppose that $\tau$ is a $t$ -corridor and $\eta$ is a $c$ -corridor. Suppose ${\hat{\tau }} \subseteq \tau$ and $\hat{\eta } \subseteq \eta$ are subcorridors. We say $\hat{\tau }$ and $\hat{\eta }$ form a bigon when they have exactly two common 2-cells, specifically their first and last ones.

A $c$ - or $t$ -corridor cannot cross itself. So, by considering an “innermost” crossing of a $c$ - and a $t$ -corridor, we observe:

Lemma 6.4. Suppose $\tau$ is a $t$ -corridor and $\eta$ is a $c$ -corridor. If $\tau$ and $\eta$ intersect more than once, then there are subcorridors $\hat{\tau } \subseteq \tau$ and $\hat{\eta } \subseteq \eta$ forming a bigon.

Per Section 3.1, a $c$ -corridor is reduced if it contains no back-to-back pair of canceling 2-cells sharing a $c$ -edge.

Lemma 6.5. In a van Kampen diagram where $c$ -corridors are reduced, if a $t$ -corridor $\tau$ intersects a $c$ -corridor $\eta$ , it will do so only once.

Proof. Since $c$ -corridors are made up of a single kind of 2-cell (arising from the defining relation $c^t=cz$ ), all 2-cells in a reduced $c$ -corridor have the same labels and are oriented the same way along the corridor. Let us assume for the contradiction that $\eta$ is reduced and that $\tau$ and $\eta$ intersect at least twice.

By Lemma 6.4, there exist subcorridors $\hat{\tau }$ and $\hat{\eta }$ that form a bigon, with precisely the first and final 2-cells, $E_1$ and $E_2$ , in common, as in Figure 9. The orientation of the edges labeled by $t$ in $E_1$ fixes an orientation for all the $t$ -labeled 1-cells along the bottom of $\hat{\eta }$ (see Remark 3.2) since $\hat{\eta }$ is reduced. It also fixes an orientation for $t$ -labeled 1-cells in $\hat{\tau }$ . But these two specifications are inconsistent for the $t$ -labeled 1-cells in $E_2$ .

We will use the same argument for alternating corridors and $c$ -corridors in Lemma 6.10 (1) and for $\alpha$ - and $t$ - partial corridors in Lemma 6.10 (4).

Figure 9. If a $t$ -corridor and a $c$ -corridor cross at least twice, the $c$ -corridor cannot be reduced.

Corollary 6.6. In a van Kampen diagram with reduced $c$ -corridors, there are no $c$ -annuli, and $t$ -annuli do not intersect $c$ -corridors.

Proof. The word around the outside of a $c$ -annulus contains $t$ ’s, so it would have to intersect once (and therefore intersect at least twice) with a $t$ -corridor, which is impossible by Lemma 6.5. Similarly, if a $c$ -corridor has common 2-cells with a $t$ -annulus, it must have at least two in common—again impossible by Lemma 6.5.

The following corollary allows us to determine the lengths of $c$ -corridors in a diagram $\Delta$ in terms of the word around its boundary and the way $c$ -edges are paired up by $c$ -corridors—the so-called $c$ -corridor pairing (see Definition 6.11).

Corollary 6.7. Suppose $\Delta$ is a van Kampen diagram with reduced $c$ -corridors. Suppose further that its boundary word is $w_1c^{\pm 1}w_2c^{\mp 1}$ for some words $w_1$ and $w_2$ and that $\eta$ is a $c$ -corridor beginning and ending on the edges labeled by these distinguished $c^{\pm 1}$ . Then the length of $\eta$ is the absolute value of the index sum of the $t^{\pm 1}$ in $w_1$ (or, equivalently, in $w_2$ ).

Proof. All $t$ -corridors intersecting $\eta$ have the same orientation with respect to $\eta$ . In particular, the word along one side of $\eta$ is $t^k$ for some $k$ , without any free reductions. Thus, the $t$ -corridors starting at $t$ -edges in $w_2$ that are oppositely oriented to the $t$ ’s in $\eta$ cannot cross it, and so must have oppositely oriented partners on the same side of $\eta$ , as shown in Figure 10. This leaves exactly the absolute value of the index sum of $t$ in $w_1$ many $t$ -corridors which have no partners on the same side of $\eta$ , and so must cross it. By Lemma 6.5, each of these $t$ -corridors can cross $\eta$ exactly once.

Since $c$ -corridors cannot cross, removing all the $c$ -corridors leaves a set of connected subdiagrams called $c$ -complementary regions. The words around the perimeters of each of these regions contain no $c^{\pm 1}$ . See Figure 11a.

Figure 10. The $t$ -corridors of oppositely oriented $t$ -edges in $w_2$ cannot cross $\eta$ .

Corollary 6.8. Let $R$ be a $c$ -complementary region in a van Kampen diagram for the word $w$ . If the word around the perimeter of $R$ is $v$ , then $|v|\leq (1+|z|)|w|$ , where $z$ is from the defining relation $c^t=cz$ for $M_{\Xi }$ .

Proof. Suppose that after cyclic conjugation $w$ has the form $x_0c^{\epsilon _0} v_0c^{-\epsilon _0}x_1c^{\epsilon _1}v_1 c^{-\epsilon _1}\cdots x_nc^{\epsilon _n}v_nc^{-\epsilon _n}$ , where $x_0,\ldots, x_n$ form part of the perimeter of the $c$ -complementary region $R$ and $v_0, \ldots, v_n$ are words in $\{a^{\pm 1}, b^{\pm 1}, c^{\pm 1}, t^{\pm 1}\}$ . Then the perimeter of $R$ can be labeled by the word $v=x_0 v'_0x_1v'_1\cdots x_nv'_n$ where $x_0,x_1,\ldots, x_n$ are part of $w$ and $v'_0, \ldots, v'_n$ label the $c$ -corridors, with $v'_i = c^{\epsilon _i}v_ic^{-\epsilon _i}$ (see Figure 11b). By Corollary 6.7, the length of each $c$ -corridor is the index sum of $t$ in the corresponding boundary word $v_i$ . Along the top of a $c$ -corridor of length $k_i$ , we have the word $(tz^{-1})^{k_i}$ , so $|v'_i| \leq (1+|z|)|v_i|$ , and so $|v|\leq (1+|z|)|w|$ .

6.3. Alternating corridors

When

\begin{equation*}M_{\Xi } \ = \ \langle a, b,c, t \mid a^{t}=ab^{k}, \ b^{t}=b,\ c^{t}=c a^lb^m, \ [a,b]=1\rangle \end{equation*}

for some $k, l, m \in \mathbb{Z}$ , killing $b$ maps $M_{\Xi }$ onto

\begin{equation*}Q_l \ \;:\!=\; \ \langle a, c, t \mid a^t=a, \ c^t = ca^l \rangle .\end{equation*}

The elements $b$ and $c$ do not commute in $M_{\Xi }$ , so $M_{\Xi }$ is not a central extension of $Q_l$ . Nevertheless, we will use a variant of the electrostatic model to establish upper bounds on area in $M_{\Xi }$ . The purpose of this section is to provide necessary preliminaries concerning van Kampen diagrams over $Q_l$ . We begin with the case $l=1$ . Setting $\alpha \;:\!=\; ta^{-1}$ , we see that

\begin{equation*}{Q}' \ \;:\!=\; \ \langle \alpha, c, t \! \mid \! \alpha ^t=\alpha, \, t^c = \alpha \rangle \end{equation*}

and $Q_1$ are the same group.

Definition 6.9. A $c$ -face is a 2-cell in a van Kampen diagram $\Delta$ over ${Q}'$ corresponding to the defining relation $t^c = \alpha$ . Partial $\alpha$ - and $t$ -corridors in $\Delta$ fit together in an alternating way: where a partial $\alpha$ -corridor ends at a $c$ -face in the interior of a diagram, a partial $t$ -corridor begins, and where this ends, another partial $\alpha$ -corridor begins. An alternating corridor in $\Delta$ is a maximal union of $\alpha$ -partial corridors, $t$ -partial corridors, and the $c$ -faces between them, fitting together in this way—see Figure 12.

Figure 11. c-Complementary regions.

Figure 12. An alternating corridor.

Like a standard corridor, an alternating corridor either closes up or connects two boundary edges (see Section 3.1). It is possible for alternating corridors to self-intersect, but, as we will see shortly, in a reduced diagram, alternating corridors do not self-intersect or close up. Every face in $\Delta$ is part of some alternating corridor. Like standard and partial corridors, an alternating corridor has a top and a bottom: the internal $\alpha$ - and $t$ -edges are directed from the bottom to the top (again, see Figure 12).

Lemma 6.10. Suppose $\Delta$ is a van Kampen diagram over $\langle \alpha, c, t \! \mid \! \alpha ^t=\alpha,\, t^c = \alpha \rangle$ in which all $c$ -corridors and all $\alpha$ - and $t$ -partial corridors are reduced (see Figures 13 and 14). Then in $\Delta$ :

1. 1. A $c$ -corridor $\eta$ and an alternating corridor $\tau$ can cross at most once.

2. 2. Alternating corridors do not close up.

3. 3. A single alternating corridor can never cross itself.

4. 4. Two alternating corridors cannot cross more than once.

Proof. For (1), it suffices (see Lemma 6.4) to prove that it is impossible to have a bigon of an alternating corridor $\tau$ and a $c$ -corridor $\eta$ in $\Delta$ . Since $c$ -corridors in $\Delta$ are reduced, the top of the $c$ -corridor is labeled by a power of $\alpha$ without any free reduction. As in our proof of Lemma 6.5, $\tau$ and $\eta$ specify inconsistent orientations for the $t$ edge in the second common 2-cell, as in Figure 15a.

Figure 13. Non-reduced subdiagrams that can occur in $\Delta$ .

Figure 14. Non-reduced subcorridors not occurring in $\Delta$ .

For (2), suppose for a contradiction, that there is an alternating corridor $\mathcal{A}$ that closes up. It cannot contain any $c$ -faces, as this would force a $c$ -corridor to cross $\mathcal{A}$ twice. If $\mathcal{A}$ contains no $c$ -faces, then it is either a $t$ - or $\alpha$ -annulus. The word along the top of the annulus is a power of $\alpha$ or $t$ , respectively. Such an annulus would imply that $t$ or $\alpha$ have finite order, but both are infinite order elements of $Q^{\prime }$ .

Figure 15. Impossible behavior for alternating corridors.

For (3), suppose for a contradiction that an alternating corridor $\eta$ has a self-intersection. An alternating corridor can only have a self-intersection at a 2-cell corresponding to the relation $[\alpha, t]=1$ . Let $\hat{\eta } \subset \eta$ be a subcorridor of $\eta$ that begins and ends at the self-intersection. Call this first and final 2-cell $E$ .

The 2-cell $E$ is part of both $t$ - and $\alpha$ - partial corridors in $\hat{\eta }$ ; therefore, $\hat{\eta }$ contains at least one $c$ -face (in particular, an odd number of $c$ -faces in order to get both an $\alpha$ - and $t$ -segment at the intersection). Each $c$ -face in $\hat{\eta }$ is part of a $c$ -corridor. By (1), $c$ -corridors can only cross $\hat{\eta }$ once, but each $c$ -corridor must cross $\hat{\eta }$ at least twice, since it cannot terminate within the region enclosed by $\hat{\eta }$ , see Figure 15b.

For (4), assume for the contradiction that two alternating corridors cross at least twice. Again, we can find a bigon of alternating corridors. There are two cases. In one, no $c$ -corridors intersect the bigon. In this case, one of the alternating corridors is a partial $t$ -corridor, and the other is a partial $\alpha$ -corridor. An argument like Lemma 6.5 shows that this kind of double intersection is impossible when $t$ - and $\alpha$ - partial corridors are reduced (see Figure 15c). In the other case, at least one $c$ -corridor intersects the bigon. We look at the triangle formed by the two bigons and the first $c$ -corridor to cross them. Since it is the first such $c$ -corridor, we have an $\alpha$ - and $t$ -partial corridor that both need to end on the same side of a $c$ -corridor. However, $c$ -corridors always have $t$ ’s along the bottom and $\alpha$ ’s along the top—there cannot be both $\alpha$ ’s and $t$ ’s on the same side of the $c$ -corridor. Figure 15d illustrates this contradiction. Therefore, neither case happens.

6.4. Quadratic area diagrams over $Q_1$

Definition 6.11. A $c$ -pairing for a word $w$ is any pairing off of the $c$ in $w$ with the $c^{-1}$ in $w$ .

If $w$ represents the identity in $M_{\Xi }$ , then a van Kampen diagram $\Delta$ for $w$ induces a $c$ -pairing: some $c$ and some $c^{-1}$ are paired when they are joined by a $c$ -corridor in $\Delta$ . We say that a $c$ -pairing is valid if it is induced by a van Kampen diagram for $w$ .

This notion of validity has content. Not all $c$ -pairings need be valid, and valid $c$ -pairings need not be unique.

Because

\begin{equation*}{Q} \ \;:\!=\; \ {Q}_1 \ = \ \langle a, c, t \mid a^t=a, \ c^t = ca \rangle \end{equation*}

is a free-by-cyclic group, its Dehn function is quadratic [8]. The point of the following lemma is that this quadratic area bound can be realized on diagrams witnessing any prescribed valid $c$ -pairing.

Lemma 6.12. There exists $A \gt 0$ such that for any word $u$ representing the identity in $Q$ (not necessarily freely reduced), and for any valid $c$ -pairing $P$ of $u$ , there is a van Kampen diagram $\theta$ for $u$ over $Q$ that induces $P$ , has $\textrm{Area}(\theta ) \leq A |u|^2$ , and has reduced $c$ -corridors.

Proof. Let $\Delta$ be a van Kampen diagram for $u$ over $Q$ that realizes the given $c$ -pairing.

Instead of $Q$ we will work with

\begin{equation*}{Q}' \ \;:\!=\; \ \langle \alpha, c, t \! \mid \! \alpha ^t=\alpha, \, t^c = \alpha \rangle,\end{equation*}

which, recall, we can see presents the same group by setting $\alpha \;:\!=\; ta^{-1}$ .

Two finite presentations $\langle A_1 \mid R_1 \rangle$ and $\langle A_2 \mid R_2 \rangle$ of the same group have $\simeq$ -equivalent Dehn functions [1, 15]. In outline, the proofs in [1, 15] go as follows. For each $a \in A_1$ , pick a word $u_a=u_a(A_2)$ representing the same group element. Suppose a word $w_1 = w_1(A_1)$ represents $1$ in $\langle A_1 \mid R_1 \rangle$ . Let $w_2$ be the word obtained from $w_1$ by replacing all of its letters $a^{\pm 1}$ by ${u_a}^{\pm 1}$ . A van Kampen diagram $w_1$ over $\langle A_1 \mid R_1 \rangle$ can be converted to a van Kampen diagram for $w_2$ over $\langle A_2 \mid R_2 \rangle$ of comparable area by converting each edge labeled $a$ to a path labeled $u_a$ and then filling all the faces. Each relator in $R_1$ can be rewritten as a word representing the identity in $A_2$ , and each can then be filled with at most some constant number of relators in $R_2$ , so the area of the diagram over $\langle A_2 \mid R_2 \rangle$ will be no more than a constant multiple of the area of the diagram over $\langle A_1 \mid R_1 \rangle$ .

In the instance of $Q$ and ${Q}'$ , the $c$ -pairings induced by the two diagrams agree, and so it suffices to prove the lemma for ${Q}'$ instead of $Q$ .

Given $u=u(a,c,t)$ , let $u'$ be the word obtained from $u(\alpha ^{-1} t, c,t)$ by canceling away all $\alpha ^{\pm 1} \alpha ^{\mp 1}$ and all $t^{\pm 1} t^{\mp 1}$ (but not all $c^{\pm 1} c^{\mp 1}$ ). Then $|u^{\prime }|\leq 2|u|$ . Construct a van Kampen diagram $\theta '$ for $u'$ over ${Q}'$ as follows. Begin with a planar polygon with edges directed and labeled so that one reads $u'$ around the perimeter. Insert reduced $c$ -corridors of 2-cells (each with perimeter $t^c \alpha ^{-1}$ ) mimicking the pattern of $c$ -corridors in $\Delta$ . Fill the complementary regions with minimal area sub-diagrams over $\langle \alpha, t \mid \alpha ^t =\alpha \rangle$ . The words around their perimeters represent the identity in $\langle \alpha, t \mid \alpha ^t =\alpha \rangle$ because the words around the corresponding loops in $\Delta$ represent the identity in $\langle a, t \mid a^t = a \rangle$ . Since the complementary regions are filled with minimal area subdiagrams, all $\alpha$ - and $t$ - partial-corridors in $\theta '$ are reduced.

Lemma 6.10 implies that the length of any alternating corridor $\mathcal{A}$ in our diagram is bounded above by the total number of $c$ -corridors and alternating corridors that intersect $\mathcal{A}$ . Since there are in total no more than $|u'|/2$ $c$ -corridors and alternating corridors, the length of $\mathcal{A}$ is at most $|u'|/2$ . Similarly, the length of each $c$ -corridor is at most $|u|/2$ by Corollary 6.7, and there are fewer than $|u|/2$ many $c$ -corridors. So altogether,

\begin{equation*}\textrm {Area}(\theta ^{\prime }) \ \leq \ \frac {|u'|^2 + |u|^2}{4} \ \leq \ 2|u|^2.\end{equation*}

6.5. Quadratic area diagrams over $Q_l$

In the previous section, we established that given a valid $c$ -pairing for a word representing the identity in $Q_1$ , we can construct a quadratic area van Kampen diagram with that $c$ -pairing. In this section, we leverage Lemma 6.12 to the case where we have a valid $c$ -pairing for a word representing the identity in $Q_l$ . Our main strategy is to rewrite words representing the identity in $Q_l$ to words in $Q_1$ , where we can apply Lemma 6.12 to build a van Kampen diagram. Then, we convert it to a diagram over $Q_l$ .

Recall that

\begin{equation*}Q_l \ \;:\!=\; \ \langle a, c, t \mid a^t=a, \ c^t = ca^l \rangle .\end{equation*}

Define

\begin{equation*}{Q}^{\tau }_{1} \ \;:\!=\; \ \langle a, c, \tau | a^{\tau }=a, c^{\tau }=ca\rangle .\end{equation*}

Identifying $t$ with $\tau ^l$ gives an isomorphism of $Q_{l}$ with the index $l$ subgroup of $Q^{\tau }_{1}$ generated by $a,c,$ and $\tau ^l$ .

Proposition 6.13. If $u$ is a (not necessarily freely reduced) word representing the identity in ${Q}_l$ and $P$ is a valid $c$ -pairing of $u$ , there exists a van Kampen diagram for the corresponding word $v\;:\!=\;u(a,c,\tau ^l)$ in $Q_1^{\tau }$ with a corresponding $c$ -pairing.

Proof. Suppose $u(a,c,t)$ represents the identity in ${Q}_l$ and $\theta _0$ is a van Kampen diagram over ${Q}_l$ for $u$ inducing the $c$ -pairing $P$ . Define $v\;:\!=\;u(a,c,\tau ^l)$ —that is, obtain $v$ by substituting a $(\tau ^l)^{\pm 1}$ for every $t^{\pm 1}$ in $u$ . Then, $v$ represents the identity in ${Q}_{1}^{\tau } = \ \langle a, c, \tau | a^{\tau }=a, c^{\tau }=ca\rangle$ and $P$ induces a valid $c$ -pairing for $v$ (which we will also call $P$ ) since $\theta _0$ can be converted to a van Kampen diagram for $v$ over ${Q}_{1}^{\tau }$ with the same pattern of $c$ -corridors as follows. First replace each $t$ -edge in $\theta _0$ by a concatenation of $l$ $\tau$ -edges. The resulting diagram has 2-cells of two types—those originating from the relation $a^t=a$ and those from the relation $c^t=ca^l$ . The perimeter words of these 2-cells become $a^{\tau ^l}a^{-1}$ and $c^{\tau ^l}(ca^{l})^{-1}$ . These words are relators in ${Q}_{1}^{\tau }$ : the first can be derived by $l$ applications of $a^{\tau }=a$ and the second by $l$ applications of $c^{\tau }=ca$ and $l(l-1)/2$ applications of $a^{\tau }=a$ . Accordingly, refine the diagram by replacing the $a^{\tau ^l}a^{-1}$ 2-cells with an $a$ -corridor of $l$ 2-cells each labeled $a^{\tau } a^{-1}$ , and the $c^{\tau ^l}(ca^{l})^{-1}$ 2-cells with a $c$ -corridor of $l$ 2-cells labeled $c^{\tau }(ca)^{-1}$ together with $l(l-1)/2$ of the $a^{\tau } a^{-1}$ 2-cells. The substitutions in the case $l=3$ are shown in Figure 16. This process maintains the $c$ -pairing during the change from $\mathcal{Q}_l$ to $\mathcal{Q}_1^{\tau }$ .

After producing a quadratic area van Kampen diagram for $v$ in $Q_1^{\tau }$ that has $c$ -pairing $P$ , we want to use it to build a quadratic area van Kampen diagram for $u$ in $Q_l$ that also has $c$ -pairing $P$ . The following lemma tells us that we will be able to replace $c$ -corridors over $Q_1^{\tau }$ with $c$ -corridors over $Q_l$ , as they always occur in multiples of $l$ .

Figure 16. Converting $\theta _0$ from $Q_l$ to $Q_1^{\tau }$ (illustrated with $l=3$ ).

Lemma 6.14. Suppose $\theta$ is a van Kampen diagram for a word $v = v(a, c, \tau ^l)$ over ${Q}^{\tau }_{1} = \langle a, c, \tau | a^{\tau }=a, c^{\tau }=ca\rangle$ , with reduced $c$ -corridors. Then, every $c$ -corridor in $\theta$ has length a multiple of $l$ .

Proof. Let $\mathcal{T}$ be the tree dual to the $c$ -corridors in $\theta$ —that is, $\mathcal{T}$ has a vertex dual to each $c$ -complementary region and an edge dual to each $c$ -corridor; the leaves of $\mathcal{T}$ correspond to regions which have one single $c$ -corridor in their perimeter (see Section 3.1). Pick any leaf $r$ of $\mathcal{T}$ to serve as the root, marked in blue in the figure. There is a bijection between vertices $v \neq r$ of $\mathcal{T}$ and $c$ -corridors $C_v$ : take $C_v$ to be dual to the first edge of the geodesic in $\mathcal{T}$ from $v$ to $r$ . This situation is illustrated in Figure 17. Each line represents a $c$ -corridor, and a vertex is drawn in each $c$ -complementary region.

Figure 17. The tree $\mathcal{T}$ dual to the $c$ -corridors of a diagram $\theta$ , with root $r$ (chosen to have degree 1). The index sum of $\tau$ around the $c$ -complementary region dual to $v$ is zero. By the induction hypothesis, the length and thus index sum of $\tau$ along the child corridors $C_{v_i}$ are multiples of $l$ , and along the boundary of $\theta$ making up the complementary region dual to $v$ are also multiples of $l$ , so the length and thus index sum of $\tau$ along $C_v$ is a multiple of $l$ .

We will show by reverse induction on distance in $\mathcal{T}$ (i.e. starting from the leaves furthest down the tree and working toward $r$ ) that the length of $C_v$ is a multiple of $l$ . Indeed when $v$ is a leaf, the argument of Corollary 6.7 implies the length of $C_v$ is given by the index sum of $\tau ^{\pm 1}$ in the boundary between the paired $c$ -edges, and $\tau$ only appears in multiples of $l$ in $v$ , so the result holds. For the induction step, suppose $v \neq r$ . The length of $C_v$ is the exponent sum of the lengths of $C_{v_i}$ (with appropriate signs) over every child $v_i$ of $v$ (each a multiple of $l$ , by induction hypothesis) and of the $\tau ^l$ in the boundary of $\theta$ that are also in the boundary of the subdiagram dual to $v$ .

Next, we examine how to build a filling for a $c$ -complementary region over $Q_{l}$ from a filling for a $c$ -complementary region over $Q_{1}^{\tau }$ when their boundaries are compatible in that the $\tau$ in the boundary of the latter occur in powers of $l$ .

Lemma 6.15. Suppose $w = w(a, \tau ^l)$ has a van Kampen diagram $\mathcal{D}$ over $\langle a, \tau \mid a^\tau = a \rangle$ of area $A$ . Then $w(a, t)$ has a van Kampen diagram $\mathcal{D}''$ over $\langle a, t \mid a^t=a \rangle$ of area at most $A$ .

Proof. Define a $\tau$ -segment to be $l$ consecutive $\tau$ -labeled edges in the boundary circuit of $\mathcal{D}$ . Such segments have a natural orientation that agrees with the orientation of the constituent $\tau$ . We will find a van Kampen diagram for $w$ over $\langle a, \tau \mid a^\tau = a \rangle$ for which the $\tau$ -segments are connected by blocks of parallel $\tau$ -corridors. (Call this a $\tau ^l$ -pairing.)

The first edge in any $\tau$ -segment can only be paired with a $\tau$ -corridor in $\mathcal{D}$ with the first edge of an oppositely oriented $\tau$ -segment. Indeed, suppose that an initial $\tau$ in a $\tau$ -segment is connected by a corridor $C$ to a $\tau$ in position $i$ on another segment, with $1\leq i \leq l$ . Let $\widehat{w}$ be the subword of $w$ between them, as shown in Figure 18a. Because $\tau$ corridors do not cross, the $\tau$ -index sum of $\widehat{w}$ must be zero. If $i \neq 1$ , the $\tau$ -index sum of $\widehat{w}$ will not be a multiple of $l$ , as $\widehat{w}$ either includes an entire $\tau$ -segment or entirely misses it, except for the partial segment which contains the $\tau$ in position $i$ . In particular, the index sum of $\tau$ in $\widehat{w}$ can only be 0 when $i=1$ .

Figure 18. In a word $w$ on $a$ and $\tau ^l$ , there is a valid $\tau$ -pairing that pairs whole $\tau$ -segments.

Construct a new van Kampen diagram $\mathcal{D}'$ for $w$ over $\langle a, \tau \mid a^\tau = a \rangle$ as follows. Begin with a planar loop with edges labeled so that we read $w(a, \tau ^l)$ around the perimeter. Add in all initial $\tau$ corridors from $\mathcal{D}$ . If an initial $\tau$ -corridor $C$ connects $\tau$ -segments $S$ and $S'$ , we will pair each $\tau$ in $S$ to the corresponding $\tau$ in $S'$ using copies of $C$ , as in Figures 18b and 19c. The remaining regions that have to be filled have perimeters labeled by words on $a^{\pm 1}$ alone, as all $\tau$ edges have been paired. Moreover, the index sum of $a$ is zero, so these can be folded together to complete the construction of $\mathcal{D}'$ without the addition of any further 2-cells.

Figure 19. A toy example of the procedure of Lemma 6.15 (illustrated with $l=3$ ).

The area of $\mathcal{D}'$ will be $l$ times the sum of the initial $\tau$ -corridor contributions, and so in particular, the area of the new diagram is at most $l A$ . Let $\mathcal{D}''$ be the van Kampen diagram for $w(a,t)$ over $\langle a, t \mid a^t = a \rangle$ of area at most $A$ obtained by replacing each stack of $l$ $\tau$ -corridors in $\mathcal{D}'$ by a single $t$ -corridor and each $\tau$ -segment in the boundary by a single $t$ -edge, as in Figure 19d.

We will promote Lemma 6.12 to the following result concerning ${Q_l = \langle a, c, t\,| a^t=a, c^t=ca^l \rangle }.$

Proposition 6.16. There exists $A_l \gt 0$ such that if $u$ is a (not necessarily freely reduced) word representing the identity in ${Q}_l$ and $P$ is a valid $c$ -pairing of $u$ , then there exists a van Kampen diagram $\theta$ for $u$ over ${Q}_l$ which has reduced $c$ -corridors, induces $P$ , and has $\textrm{Area}(\theta ) \leq A_l |u|^2$ .

Proof. Suppose $u(a,c,t)$ represents the identity in ${Q}_l$ and $u$ has a valid $c$ -pairing $P$ . Proposition 6.13 implies that $P$ is also a valid $c$ -pairing for the corresponding word $v\;:\!=\;u(a,c,\tau ^l)$ in $Q_1^{\tau }$ , which we get by substituting a $(\tau ^l)^{\pm 1}$ for every $t^{\pm 1}$ in $u$ . Now we can use what we know about building diagrams over $Q_1^{\tau }$ : by Lemma 6.12, there is a constant $A_1\gt 0$ such that $v$ admits a new van Kampen diagram $\theta _{1}$ over ${Q}_{1}^{\tau }$ that induces $P$ and has area at most $A_1{|{v}|^2} \leq A_1 l^2{|u|}^2$ . Guided by $\theta _{1}$ , we will construct a van Kampen diagram $\theta _{l}$ for $u$ over ${Q}_{l}$ which has comparable area.

By Lemma 6.14, $c$ -corridors in $\theta _1$ all have length that is a multiple of $l$ . To build $\theta _{l}$ , we begin by inserting reduced $c$ -corridors into a polygonal path labeled by $u$ , mimicking the $c$ -corridors in $\theta _1$ . Corresponding $c$ -corridors in the two diagrams differ in length by exactly the factor $l$ : where a $c$ -corridor in $\theta _1$ has $\tau ^{nl}$ along one side and $(\tau a^{-1})^{nl}$ along the other, the corresponding $c$ -corridor in $\theta _l$ has $t^n$ along one side and $(t a^{-l})^{n}$ along the other.

Next, we fill the $c$ -complementary regions. We wish to use Lemma 6.15 to convert the filling in $c$ -complementary regions of $\theta _1$ to fillings in $\theta _l$ , but for any $c$ -complementary region, the word along the perimeter of the region will not generally have an appropriate form. Its perimeter has the form $x_0(\tau a^{\epsilon _1})^{l k_1} x_1 \cdots (\tau a^{\epsilon _n})^{lk_n}x_n$ , where $\epsilon _i \in \{0, -1\}$ , $k_i \neq 0$ , and $x_i$ is a subword of $v$ and therefore is a word in $a$ and $\tau ^l$ , as in Figure 20. We add a collar of $2$ -cells to change the boundary of the $c$ -complemetary region to $x_0 (\tau ^l a^{\epsilon _1 l})^{k_1} x_1 \cdots (\tau ^l a^{\epsilon _n l})^{k_n}x_n$ . In particular, if $L$ is a minimal area diagram for the word $(\tau a^{-1})^{l}(\tau ^la^{-l})^{-1}$ , then $k_i$ copies of $L$ can be glued in to rewrite $(\tau a^{\epsilon _i})^{l k_i}$ to $(\tau ^l a^{\epsilon _i l})^{k_i}$ . The result is a region with boundary that is a word in $a$ and $\tau ^l$ .

Apply Lemma 6.15 to convert each of these diagrams, without increasing area, to diagrams over $\langle a, t \mid a^t =a \rangle$ with boundary $x_0(t a^{l \epsilon _1})^{k_1} x_1 \dots (t a^{l\epsilon _n})^{k_n}x_n$ (as in Figure 21d), and use them to fill the $c$ -complementary regions of $\theta _l$ . This produces a van Kampen diagram $\theta _l$ for $u$ over ${Q}_l$ .

Figure 20. The quadratic area diagram $\theta _1$ .

Figure 21. Converting a $c$ -complementary region filling from $\theta _1$ over ${Q}_1^{\tau }$ to one for $\theta _l$ over ${Q}_l$ .

Finally, we come to area estimates for $\theta _l$ . First, observe that the total number of 2-cells in the $c$ -corridors in $\theta _1$ is at most the area of $\theta _1$ , which we determined earlier to be at most $A_1 l^2{|u|}^2$ . Correspondingly, there are at most $A_1 l{|u|}^2$ 2-cells in the $c$ -corridors in $\theta _l$ . The number of copies of $L$ glued on to the $c$ -complementary regions is at most $A_1 l{|u|}^2$ , since it is the sum of the lengths of the $c$ -corridors, divided by $l$ . Since $L$ has area bounded above by $l^2$ , the total area taken by copies of $L$ is at most $A_1 l^3{|u|}^2$ . The total area of the $c$ -complementary regions in $\theta _1$ is also at most $A_1 l^2{|u|}^2$ . They, along with the attached copies of $L$ , are converted to the $c$ -complementary regions in $\theta _l$ without an increase in their area, as per Lemma 6.15. Therefore, the area of $\theta _l$ is at most $A_1 l{|u|}^2 + A_1 l^3{|u|}^2 + A_1 l^2{|u|}^2 \leq A_l |u|^2$ , where $A_l \;:\!=\; A_1(l + l^3+ l^2)$ .

6.6. Completing our proof of Theorem B

Proof of Theorem B (1). This is the case where $\phi$ has finite order. By Lemma 6.1 and Proposition 6.2, for the purposes of determining the Dehn function of $M_{\Phi }$ , and thus $M_{\Psi }$ , we can work with $M_{\Xi }$ , which has the form:

\begin{align*}M_{0, l, m} & \;:\!=\; \langle a, b,c, t \mid [a,b]=1, \ a^{t}=ab^{0}, \ b^{t}=b,\ c^{t}=c a^lb^m \rangle \nonumber \\[5pt] & \;= \langle a, b,c, t \mid [a,b]=[a,t] = [b,t]=1,\ c^{t}=c a^lb^m \rangle \end{align*}

for some $l, m \in \mathbb{Z}$ . Let

\begin{equation*}N_l \ \;:\!=\; \ \langle a, c, t \mid a^t=a, \ c^t = ca^l \rangle .\end{equation*}

These groups are not hyperbolic, so their Dehn functions grow at least quadratically. We will show that these mapping tori have quadratic Dehn functions for all $l, m \in \mathbb{Z}$ . All proofs of the quadratic upperbounds for these groups can be reduced to the proof for $M_{0,l,0} = \langle a, b,c, t \mid [a,b]=[a,t]=[b,t]=1,\ c^{t}=c a^l \rangle$ . We begin by considering this special case, which has the property that $b$ -corridors have the same words along their top and their bottom sides.

Suppose $w$ is a word representing the identity in $M_{0,l,0}$ . Let $\Delta$ be a minimal area van Kampen diagram for $w$ over $M_{0,l,0}$ . Let $\overline{w}$ be $w$ with all $b^{\pm 1}$ removed. Then $\overline{w}=1$ in $N_l$ . Moreover, the $c$ -pairing $P$ induced by $\Delta$ in turn induces a valid $c$ -pairing $\overline{P}$ for $\overline{w}$ because collapsing each $b$ -corridor to the path along its bottom side gives a van Kampen diagram $\overline{\Delta }$ for $\overline{w}$ over $N_l$ .

By Proposition 6.16, there is a constant $A_l \gt 0$ and a van Kampen diagram $\overline{\theta }$ for $\overline{w}$ over $N_l$ which has reduced $c$ -corridors, induces $\overline{P}$ , and has area at most $A_l |\overline{w}|^2$ .

The defining relations for $N_l$ are also defining relations for $M_{0,l,0}$ (as $m=0$ ), so $\overline{\theta }$ is a fortiori a van Kampen diagram over $M_{0,l,0}$ . We aim to convert it from a van Kampen diagram for $\overline{w}$ , which contains no letters $b^{\pm 1}$ , to a van Kampen diagram $\theta$ for the original $w$ , which may contain letters $b^{\pm 1}$ . We will do this without altering its $c$ -corridors, only changing the diagrams in the $c$ -complementary regions. Indeed, in the diagram $\Delta$ , there are no partial $b$ -corridors and no $b$ -corridor can cross a $c$ -corridor. Since the pairings of $c$ -corridors in $\overline{\theta }$ agrees with that in $\overline{\Delta }$ (and so in $\Delta$ ), for each $c$ -complementary region $\overline{C}$ in $\overline{\theta }$ , there is a corresponding $c$ -complementary region in $\Delta$ .

In $\Delta$ , no $b$ -corridor can cross a $c$ -corridor and there are no partial $b$ -corridors. So, in each word around a $c$ -complementary region the $b$ and $b^{-1}$ letters are on $\partial \Delta$ and are paired off by $b$ -corridors that connect them. Therefore, each $c$ -complementary region $\overline{C}$ in $\overline{\theta }$ can be inflated to put the necessary $b$ and $b^{-1}$ in place by adding $b$ -corridors to the boundary of $ \overline{C}$ , thereby adding an annular cuff about each $c$ -complementary region, using 2-cells for the relations $[b,t]=1,$ and $[a,b]=1$ . The total number of such $b$ -corridors that we must insert over all of these diagrams is at most $|w|/2$ . The length of each $b$ -corridor is at most the length of the boundary circuit $\partial \overline{C}$ of the relevant $c$ -complementary region $\overline{C}$ in $\overline{\theta }$ . By an argument equivalent to Corollary 6.8, the boundary circuit of each $c$ -complementary region has length at most a constant times $|\overline{w}|$ , where the constant is $|l|+1$ – if the bottom of a $c$ -corridor has $t^k$ along it, the top will have $(ta^{-l})^k$ along it.

Thus, the area of the resulting diagram $\theta$ is at most the area of $\overline{\theta }$ (which is at most $A_l |\overline{w}|^2$ ) plus the number of 2-cells in $b$ -corridors, which is no more than a constant times $|\overline{w}| \, |w|$ . In total, the area of $\theta$ is at most a constant times $|w|^2$ , as required.

Now we consider the case of $M_{0, l,m}$ for $m \neq 0$ . If $l$ and $m$ are relatively prime, by Bézout’s Lemma, there is a pair of integers $(x,y)$ such that $l y - m x = 1$ . So there is a generating set $\{A, B\}$ of $\mathbb{Z}^2 = \langle a, b \rangle$ with $A= a^{l} b^{m}$ and $B= a^xb^y$ (generating since $a = A^yB^{-m}$ and $b = B^l A^{-x}$ ), for which our group has the presentation:

\begin{equation*}{\langle A, B, c, t \mid [A, B]=1, A^t =A, B^t=B, c^t=cA \rangle },\end{equation*}

the same as $M_{0,1,0}$ . Therefore, the Dehn function is quadratic. Finally, if $l$ and $m$ are not relatively prime, let $n\;:\!=\;\mbox{gcd}(l, m)$ . Then, $M_{0,l,m}$ is a subgroup of index $n$ in $M_{0,\frac{l}{n}, \frac{m}{n}}$ . But then, $M_{0,\frac{l}{n}, \frac{m}{n}}$ has a quadratic Dehn function and hence so does $M_{0,l,m}$ .

Proof of Theorem B (2). This is the case where $\phi$ has a non-unit eigenvalue. As $K\;:\!=\;\langle a, b \rangle \cong \mathbb{Z}^2$ quasi-isometrically embeds in $\mathbb{Z}^2 \ast \mathbb{Z}$ and $\Phi \left |_{K} \right. = \phi$ is an automorphism of $K$ , Lemma 3.5 implies that the Dehn function of $M_{\Phi }$ is bounded below by an exponential function. From Lemma 3.4, the Dehn functions of mapping tori of RAAGs are always bounded above by exponential functions. Thus, $M_{\Phi }$ and so $M_{\Psi }$ has exponential Dehn function.

Proof of Theorem B (3). This is the case where $\phi$ has infinite order and only unit eigenvalues. We will show that $M_{\Phi }$ and thus $M_{\Psi }$ has a cubic Dehn function. By Lemma 6.1 and Proposition 6.2, for the purposes of determining the Dehn function, we can work with $M_{\Xi }$ which has the form:

\begin{equation*}M_{k, l, m} \ \;:\!=\; \ \langle a, b,c, t \mid [a,b]=1, \ a^{t}=ab^{k}, \ b^{t}=b,\ c^{t}=c a^lb^m \rangle \end{equation*}

for some $k, l, m \in \mathbb{Z}$ with $k \neq 0$ . Let

\begin{equation*}N_l \ \;:\!=\; \ \langle a, c, t \mid a^t=a, \ c^t = ca^l \rangle .\end{equation*}

Suppose $w$ is a freely reduced word representing the identity in $M_{k,l,m}$ . Let $\Delta$ be a minimal area van Kampen diagram for $w$ over $M_{k,l,m}$ . Let $\overline{w}$ be $w$ with all $b^{\pm 1}$ removed. Then, $\overline{w}=1$ in $N_l$ . As in case 1 above, the $c$ -pairing $P$ induced by $\Delta$ induces a valid $c$ -pairing $\overline{P}$ for $\overline{w}$ .

By Proposition 6.16, there is a constant $A_l \gt 0$ dependent only on $l$ such that $\overline{w}$ admits a van Kampen diagram $\overline{\theta }$ over $N_l$ which also induces $\overline{P}$ and has area at most $A_l |\overline{w}|^2$ . Again, as in case 1 above, by Corollary 6.8, there exists a constant $K\gt 0$ such that the boundary circuit of any $c$ -complementary region $\overline{C}$ in $\overline{\theta }$ has length at most $K | \overline{w} |$ . Each such $\overline{C}$ is a diagram over $\langle a,t \mid a^t =a \rangle$ .

Now $\overline{C}$ has a maximal geodesic tree in its 1-skeleton—that is, a tree reaching all vertices and with the property that there is a root vertex $v_{\overline{C}}$ on the boundary $\partial \overline{\theta }$ such that for every vertex $v$ in $\overline{C}$ , the distance from $v_{\overline{C}}$ in the tree is the same as in the 1-skeleton of $\overline{C}$ .

We claim that the diameter of $\overline{C}$ is at most a constant times $|\overline{w}|$ . This is because every vertex in $\overline{C}$ is contained in an $a$ -corridor that extends to $\partial \overline{C}$ . The length of each $a$ -corridor is the number of $t$ -corridors that cross it, and there are at most $K |\overline{w}|/2$ many $t$ -corridors in $\overline{C}$ , because $t$ -corridors begin and end on $\partial \overline{C}$ and do not cross $c$ -corridors more than once in minimal area diagrams. Therefore, every vertex in $\overline{C}$ is within a distance of $K |\overline{w}|/2$ from $\partial \overline{C}$ . It follows that the diameter of $\overline{C}$ is at most $ (K+1)|\overline{w}|$ , as any two points in the boundary can be connected by a path of length at most $|\overline{w}|$ .

As the diameter of $\overline{C}$ is at most a constant times $|\overline{w}|$ and $|\overline{w}|\leq |w|$ , any maximal geodesic tree in its 1-skeleton has diameter at most a constant times $|w|$ .

We now apply the electrostatic model from Section 4 to inflate $\overline{\theta }$ to a van Kampen diagram for $w$ over $M_{k,l,m}$ . Since $\overline{\theta }$ induces a valid $c$ -pairing, this can be done by inserting $b$ -corridors within the $c$ -complementary regions.

First, we charge the diagram with at most $A_l \, |\overline{w}|^2 \, \max \{k, m\}$ many $b$ -charges, in effect, replacing all of the 2-cells for defining relations from $N_{l}$ with the corresponding 2-cells for defining relations from $M_{k,l,m}$ . The area is unchanged at $A_l|\overline{w}|^2$ . Next connect each charge in $\overline{C}$ by a $b$ -partial corridor of length no more than $(K+1)|\overline{w}|$ to the root $v_{\overline{C}}$ , along the maximal tree. The total area of these $b$ -partial corridors is at most a constant times $|\overline{w}|^3$ . Finally, insert $b$ -corridors (each of at most a constant times $|w|$ ) along the boundaries of the $c$ -complementary regions to rearrange the (at most a constant times $|w|^2$ many) $b$ and $b^{-1}$ until the perimeter word is $w$ .

The resulting diagram $\theta$ for $w$ over $M_{k, l, m}$ has at most the area of $\overline{\theta }$ (at most quadratic in $|\overline{w}|$ ), plus the total area of the $b$ -partial corridors (at most cubic in $|\overline{w}|$ ), plus the total area of the $b$ -corridors (at most cubic in $|w|$ )—in total, at most cubic in $|w|$ . So the Dehn function of $M_{k,l,m}$ grows at most cubically.

As $\phi$ has infinite order and only unit eigenvalues, it has a $2 \times 2$ Jordan block $A$ and so, by Lemma 3.5, the Dehn function of the mapping torus has a cubic lower bound.

7. Mapping tori of RAAGs of the product of two free groups

Here, we will prove Theorem C concerning Dehn functions of mapping tori of products $F_k \times F_l$ of free groups.

7.1. Automorphisms of $F_k \times F_l$

Suppose $X$ and $Y$ are disjoint finite sets with $\left |X\right | = k$ , $\left |Y\right | = l$ , and $k, l \geq 2$ . Let $\Gamma$ be the bipartite graph with vertex set $X \cup Y$ and an edge between a pair of vertices if and only if one is in $X$ and the other is in $Y$ . So $G= F_k \times F_l$ is the RAAG $A_{\Gamma }$ .

Our first task is to explain the opening part of Theorem C, which amounts to:

Lemma 7.1. Given $\Psi \in{\textrm{Aut}}(G)$ , we can find $\phi _1 \in{\textrm{Aut}}(F_k)$ and $\phi _2 \in{\textrm{Aut}}(F_l)$ such that $\Phi = \phi _1 \times \phi _2$ equals $\Psi$ or $\Psi ^2$ . If $k\neq l$ , then $\Phi = \Psi$ .

This lemma will allow us to work with $\Phi$ instead of $\Psi$ when finding the Dehn function of $M_{\Psi }$ , since $\delta _{M_{\Psi }} \simeq \delta _{M_{\Phi }}$ by Lemma 3.6.

For a vertex $x$ in a graph, $\textrm{star}(x)$ is the subgraph consisting of all edges incident with $x$ and $\textrm{link}(x)$ is the set of vertices adjacent to $x$ . We will prove Lemma 7.1 with the help of:

Lemma 7.2 (Laurence [18], Servatius [24]). If $A_{\Gamma }$ is a RAAG, then the following is a generating set for ${\textrm{Aut}}(A_{\Gamma })$ :

1. 1. All inner automorphisms: for a vertex $x$ of $\Gamma$ , $\iota _x\;:\;y \mapsto x^{-1} y x$ for all $y\in A_{\Gamma }$ .

2. 2. All inversions: maps that send $x \mapsto x^{-1}$ for some vertex $x$ of $\Gamma$ and leave all other vertices fixed.

3. 3. All partial conjugations: for a vertex $x$ in $\Gamma$ and a connected component $C$ of $\Gamma - \textrm{star}(x)$ , map $y\,\mapsto \,x^{-1}yx$ for all vertices $y$ in $C$ and fix all other vertices.

4. 4. All transvections: for a pair of vertices $x, y$ of $\Gamma$ such that $\textrm{link}(x) \subseteq \textrm{star}(y)$ , $\tau _{x,y}$ maps $x\,\mapsto \,xy$ and fixes all other vertices.

5. 5. All graph symmetries: automorphisms induced by the restriction of a graph symmetry to the vertex set.

We can see how this generating set reflects the product structure in the instance of $A_{\Gamma } = F_k \times F_l$ .

Corollary 7.3. Write $F_k = F(X)$ and $F_l = F(Y)$ , where $X=\left \{x_1, \dots, x_k\right \}$ and $Y=\left \{y_1, \dots, y_l\right \}$ . When $A_{\Gamma } = F_k \times F_l$ , the inner automorphisms, inversions, partial conjugations, and transvections of the Laurence–Servatius generators of ${\textrm{Aut}}(A_{\Gamma })$ are in ${\textrm{Aut}}(F_k) \times{\textrm{Aut}}(F_l)$ . The same is true of the graph symmetries, except when $k =l$ , where we get additional graph symmetries by composing with the graph symmetry $R \in{\textrm{Aut}}(A_{\Gamma })$ that exchanges $X$ and $Y$ by mapping $x_i \mapsto y_i$ and $y_i \mapsto x_i$ for all $i$ .

Proof. This is immediate for the inversions. It is true of the inner automorophisms because $[x_i, y_j]=1$ for all $i,j$ , so conjugation by a word $w=xy$ where $x\in F_k$ and $y \in F_l$ can be expressed as $\iota _w=\iota _x \times \iota _y$ . It is true of the partial conjugations similarly. As for the transvections, suppose $y \in Y$ , and so $\textrm{star}(y) = \{y\} \cup X$ . If $w \in Y,$ then $\textrm{link}(w) = X$ , and so $\textrm{link}(w) \subseteq \textrm{star}(y)$ . So $\tau _{w,y}\;:\;w \mapsto wy$ (and fixes all other elements of $X \cup Y$ ), and $\tau _{w,y}$ restricts to automorphisms of $F_k = F(X)$ and $F_l = F(Y)$ , as claimed. If, on the other hand, $w \in X$ , then since $\textrm{link}(w)=Y$ , $\textrm{link}(w) \subseteq \textrm{star}(y)$ if and only if $Y=\{y\}$ , and so, as $l \geq 2$ , there are no transvections $\tau _{w,y}$ . Likewise, the result holds for transvections $\tau _{w,x}$ with $x \in X$ . The result for graph symmetries is straightforward.

Proof of Lemma 7.1. Every automorphism $\Omega$ of $F_k \times F_l$ can be expressed as a product $\Pi$ of the Laurence–Servatius generators. (This can be done effectively: search through an enumerated list of all such products until a suitable $\Pi$ is found.)

Suppose that $k\neq l$ and that $\Psi \in{\textrm{Aut}}(G)$ . Then by Corollary 7.3, we have that $\Phi = \phi _1 \times \phi _2$ for some $\phi _1 \in{\textrm{Aut}}(F_k)$ and $\phi _2 \in{\textrm{Aut}}(F_l)$ .

Next, consider the case $k=l$ . Any $\Psi \in{\textrm{Aut}}(G)$ can be expressed as a product of the Laurence–Servatius generators. Per Corollary 7.3, each of these generators is in ${\textrm{Aut}}(F_k) \times{\textrm{Aut}}(F_k)$ , except for some of the graph automorphisms—the latter can take the form $\rho R$ where $\rho \in{\textrm{Aut}}(F_k) \times{\textrm{Aut}}(F_k)$ and $R$ is the factor-exchanging automorphism of Corollary 7.3. Accordingly, $\Psi ^2$ can be expressed as such a product in which there is an even number of $R$ terms. So $\Psi ^2$ is a product of the Laurence–Servatius generators that are in ${\textrm{Aut}}(F_k) \times{\textrm{Aut}}(F_k)$ , because $R^2 =\textrm{id}$ , and if $\tau$ is a Laurence–Servatius generator in ${\textrm{Aut}}(F_k) \times{\textrm{Aut}}(F_k)$ , then so is $R^{-1}\circ \tau \circ R$ . Then, $\Phi =\Psi ^2$ satisfies the requirements of the lemma.

Here is a further lemma we will use to adapt a RAAG automorphism to one better suited to calculation of the Dehn function of the mapping torus.

Lemma 7.4. Suppose $\phi _1, \psi _1 \in{\textrm{Aut}}(F_k)$ and $\phi _2, \psi _2 \in{\textrm{Aut}}(F_l)$ are such that $[\phi _1]= [\psi _1]$ in $\textrm{Out}(F_k)$ and $[\phi _2] =[\psi _2]$ in $\textrm{Out}(F_l)$ . Then, $\delta _{M_{\phi _1 \times \phi _2}} \simeq \delta _{M_{\psi _1 \times \psi _2}}$ .

Proof. Suppose $\phi _1 = \iota _{a}\circ \psi _1$ for $a \in F_k$ and $\phi _2 = \iota _{b}\circ \psi _2$ for $b \in F_l$ . Then viewing $a$ and $b$ as elements of $F_k \times F_l$ via the natural embeddings $F_k \to F_k \times F_l$ and $F_l \to F_k \times F_l$ , we have that $\phi _1 \times \phi _2 = \iota _{ab}\circ (\psi _1 \times \psi _2)$ , as $b$ commutes with all elements of $F_k$ and $a$ commutes with all elements of $F_l$ . So $[\phi _1 \times \phi _2]=[\psi _1 \times \psi _2]$ in $\textrm{Out}(F_k \times F_l)$ and it follows from Lemma 3.6 that $\delta _{M_{\phi _1 \times \phi _2}} \simeq \delta _{M_{\psi _1 \times \psi _2}}$ .

7.2. Growth of free group automorphisms

Suppose $F$ is a finite-rank free group. The growth $g_{\phi, X}\;:\;\mathbb{N} \to \mathbb{N}$ of an automorphism $\phi \;:\;F \to F$ with respect to a free basis $X$ is defined by:

\begin{equation*}g_{\phi, X}(n) \ \;:\!=\; \ \max _{x\in X}\{|\phi ^n(x)|\},\end{equation*}

where $|\phi ^n(x)|$ denotes the length of a shortest word on $X$ representing $\phi ^n(x)$ . We write $f \simeq _{\ell } g$ when $f, g \;:\;\mathbb{N} \to \mathbb{N}$ are Lipschitz equivalent; that is, when there exist $C_1, C_2\gt 0$ such that $C_1 g(n) \lt f(n) \lt C_2 g(n)$ for all $n$ . Up to $\simeq _{\ell }$ , free group growth $g_{\phi,X}$ does not depend on the choice of finite basis $X$ , and so we will write $g_{\phi }$ without ambiguity. We write $f \preceq _{\ell } g$ when there exists $C\gt 0$ such that $f(n)\,\lt \,Cg(n)$ for all $n$ .

Recall that we write $f \preceq g$ when there exists $C\gt 0$ such that $f(n)\lt Cg(Cn+C)+Cn+C$ for all $n$ , and we write $f \simeq g$ when $f \preceq g$ and $g \preceq f$ . Note that $f \preceq _{\ell } g$ implies $f \preceq g$ , and so $f \simeq _{\ell } g$ implies $f \simeq g$ .

We say that $\phi \in{\textrm{Aut}}( F )$ is periodic when there is $l\gt 0$ such that $\phi ^l$ is an inner automorphism. We say that $\phi$ is polynomially growing when there is $d \geq 0$ such that $g_{\phi } (n) \simeq _{\ell } n^d$ , and $\phi$ is exponentially growing otherwise.

To build van Kampen diagrams which demonstrate the lower bound on the Dehn function of $M_{\phi _1 \times \phi _2}$ , we will use a family of words $x_m$ ( $m \in \mathbb{N}$ ) and constants $C$ and $d$ such that for all $m$ ,

\begin{equation*}Cn^d|x_m|\ \leq \ |\phi ^n(x_m)|.\end{equation*}

One approach to finding these words is to consider $x_m=x^m$ for some word $x$ . However, this approach requires care in understanding cancelation, leading us to consider the growth of cyclically reduced words. Accordingly, for $g \in F$ , let $||g||$ denote the length of the shortest word representing a conjugate of $g$ (cyclically reduced length).

Levitt [19, Theorem 3] implies that when $\phi$ is polynomially growing, for every $x \in F$ , there exists $d_x \geq 0$ such that $| \phi ^n(x) | \simeq _{\ell } n^{d_x}$ , and when it is exponentially growing, there exists $x \in F$ and $\lambda \gt 1$ such that $|\phi ^n(x)| \gt \lambda ^n$ for all $n \in \mathbb{N}$ . By [19, Theorem 6.2], the corresponding result holds for $|| \, \cdot \, ||$ in place of $| \, \cdot \, |$ , though possibly with different powers and exponential functions.

Definition 7.5. If $\phi$ is polynomially growing, let $d$ be the maximum degree so that for some $g \in F(X)$ , $||\phi ^n(g)|| \simeq _{\ell } n^d$ . In this case, define $g^{cyc}_{\phi }(n) \;:\!=\; n^{d}$ . Otherwise, $||\phi ^n(g)|| \simeq _{\ell } \lambda ^n$ for some $\lambda \gt 1$ , and we define $g^{cyc}_{\phi }(n) \;:\!=\; 2^n$ .

In general, $g^{cyc}_{\phi }(n) \not \simeq _{\ell }\ \max _{x\in X}\{||\phi ^n(x)||\}$ . That is, what happens to generators does not fully determine growth rate measured in terms of cyclically reduced length. Indeed, [19, Lemma 5.2] gives a family of automorphisms $\phi _L$ and bases $X_L$ ( $L \in \mathbb{N}$ ) such that for all $x\in X_L$ , $ ||\phi ^n(x)|| \simeq _{l} n^{d_x},$ where $d_x \in \{0,1\}$ , but there exists $g \in F(X_L)$ such that $||\phi ^n(g)|| \simeq _{l} n^{L}$ .

To establish lower bounds for the Dehn function of $M_{\phi _1 \times \phi _2}$ , we will use cyclically reduced growth to find lower bounds for the growth of a family of words under repeated application of our automorphism. To establish upper bounds for the Dehn function of $M_{\phi _1 \times \phi _2}$ , we will use growth (without cyclic reduction) to provide upper bounds for the growth of words under our automorphism. Results of Levitt bridge the gap between the two types of growth: when the cyclically reduced growth and traditional growth disagree, it is possible to exchange $\phi _1 \times \phi _2$ with a related automorphism $\hat{\xi }_1 \times \hat{\xi }_2$ for which $g_{\hat{\xi _i}} \simeq g^{\text{cyc}}_{\hat{\xi _i}}$ for $i \in \{1,2\}$ , and the mapping tori $M_{\phi _1\times \phi _2}$ and $M_{\hat{\xi _1} \times \hat{\xi _2}}$ will have equivalent Dehn functions. We expand on this below.

Here is a summary of results of Levitt [19] and Piggot [23] on properties of growth and cyclically reduced growth in finite-rank free groups $F$ :

Lemma 7.6. Suppose $\phi \in{\textrm{Aut}}( F)$ .

1. 1. $g^{cyc}_{\phi }=g^{cyc}_{\psi }$ if $[\phi ] = [\psi ] \in \textrm{Out}(F)$ .

2. 2. If $\phi$ is polynomially growing, $g^{cyc}_{\phi }\simeq _{\ell }g^{cyc}_{\phi ^k}$ for all $k\in \mathbb{N}$ .

3. 3. (Theorem 0.4 of [23]) $g_{\phi } \simeq g_{\phi ^{-1}}$ .

4. 4. (By Theorem 3 of [19], using that $\alpha ^n \simeq \beta ^n \simeq n^\gamma \beta ^n$ for $\alpha, \beta \gt 1$ and $\gamma \geq 0$ ; cf. Bestvina–Feighn–Handel [2]). Either $g_{\phi }(n) \simeq 2^n$ , or $g_{\phi }(n) \simeq _{\ell } n^{d}$ for some $d\in \{0\}\cup \mathbb{N}$ .

5. 5. (Per the discussion at the start of Section 2 of [19]) If $n \mapsto ||\phi ^n(g)||$ grows polynomially, $g^{cyc}_{\phi } \simeq _{\ell } g^{cyc}_{\phi ^{-1}}$ .

6. 6. (By Corollary 1.6 of [19]) If $n \mapsto ||\phi ^n(g)||$ grows polynomially, then there exists $p\geq 1$ and $\xi \in{\textrm{Aut}}(F)$ such that $[\phi ^p] = [\xi ]$ in $\textrm{Out}(F)$ and $\xi$ admits a nontrivial fixed point.

7. 7. (By Lemma 2.3 of [19]) Suppose $\xi \in{\textrm{Aut}}(F)$ is polynomially growing and satisfies $g_{\xi }^{cyc} (n)\simeq _{\ell } n^d$ with $d\geq 1$ and $\xi$ has a nontrivial fixed point set. Then $g_{\xi }(n) \simeq _{\ell } n^d \simeq _{\ell } g_{\xi }^{cyc} (n)$ .

Proof. We will explain (7), which is the one case that is not immediate from the sources. Corollary 1.6 of [19] guarantees that for any polynomially growing $\Phi \in{\textrm{Aut}}(F)$ that is not periodic, there exists $p$ such that there is a representative $\alpha$ in the outer automorphism class of $\Phi ^p$ , such that $\alpha$ has a nontrivial fixed point. Lemma 2.3 of [19] describes necessary conditions on a polynomially growing automorphism $\xi$ under which $g_\xi \not \simeq g_\xi ^{cyc}$ . In particular, he shows that when the fixed point set is nontrivial, they are only inequivalent when $g_\xi ^{cyc}(n)$ is bounded above by a constant. A hypothesis of (7) is that $g_\xi ^{cyc}(n)$ grows at least linearly, hence the conclusion.

In building van Kampen diagrams and shuffling relators, we will use both forward and backward iterates of our automorphism. Lemma 7.6 (3) and (5) imply that we can use the same functions to estimate both. (1) implies that cyclic growth can be defined for outer automorphisms. This can fail for growth. However, the next results imply that we can nevertheless find automorphisms with equivalent growth and cyclic growth.

Lemma 7.7. Suppose $\phi \in{\textrm{Aut}}(F)$ has polynomial growth and is not periodic. Then there exists $\xi \in{\textrm{Aut}}(F)$ and $p\geq 0$ with $[\xi ] = [\phi ^p]\in \textrm{Out}(F)$ and $g^{cyc}_{\phi } \simeq g^{cyc}_{\xi } \simeq g_{\xi }$ . Moreover, for any $q\geq 1$ , $g^{cyc}_{\phi } \simeq g^{cyc}_{\xi ^q} \simeq g_{\xi ^q}$ .

Proof. We use Lemma 7.6: take $\xi$ as per (6) and then apply (7), (1), and (2) to get that $g^{cyc}_{\phi } \simeq _{\ell } g^{cyc}_{\xi ^q} \simeq _{\ell } g_{\xi ^q}$ , and therefore $g^{cyc}_{\phi } \simeq g^{cyc}_{\xi ^q} \simeq g_{\xi ^q}$ .

Lemma 7.8. Suppose $\phi _1 \in{\textrm{Aut}}(F_k)$ and $\phi _2 \in{\textrm{Aut}}(F_l)$ . For $i =1,2$ , suppose $p_i \geq 0$ is such that $[\phi _i^{p_i}] = [\xi _i]$ as in Lemma 7.7. Define $\hat{\xi }_1 = \xi _1^{p_2}, \,\hat{\xi }_2 = \xi _2^{p_1}$ . Then, $M_{\phi _1\times \phi _2}$ and $M_{\hat{\xi }_1\times \hat{\xi }_2}$ have equivalent Dehn functions and $g_{\phi _i}^{cyc} \simeq g_{\hat{\xi }_i}^{cyc} \simeq g_{\hat{\xi }_i}$ .

Proof. By Lemma 3.6, the Dehn functions of $M_{\phi _1 \times \phi _2}$ and $M_{(\phi _1 \times \phi _2)^{p_1p_2}} = M_{(\phi _1^{p_1})^{p_2} \times (\phi _2^{p_2})^{p_1}}$ are equivalent. By Lemma 7.4, we may also pick convenient representatives of the outer automorphism classes without changing the Dehn function. So $M_{\xi _1^{p_2} \times \xi _2^{p_1}} = M_{\hat{\xi }_1\times \hat{\xi }_2}$ also has equivalent Dehn function to $M_{\phi _1 \times \phi _2}$ .

7.3. Dehn function lower bounds

A result similar to Lemma 7.9 was proved by Brady and Soroko in Proposition 3.4 in [6] in the context of Bieri doubles. The notation $\simeq _{\ell }$ , $\preceq _{\ell }$ , and $\preceq$ is from the start of Section 7.2 above.

Lemma 7.9. Suppose that $\Phi \in{\textrm{Aut}}(F_k \times F_l)$ has the form $\Phi =\phi _1 \times \phi _2$ where $\phi _1 \in{\textrm{Aut}}(F_k)$ and $\phi _2 \in{\textrm{Aut}}(F_l)$ . Suppose that $g_{\phi _1}^{cyc} \preceq _{\ell } g_{\phi _2}^{cyc}$ . We can bound the Dehn function $\delta _{M_{\Phi }}$ of $M_{\Phi }$ as follows.

1. 1. If $g_{\phi _1}^{cyc}(n) \simeq _{\ell } n^{d_1}$ , for some $d_1\geq 0$ , then $n^{d_1 +2} \ \preceq \ \delta _{M_{\Phi }}(n).$

2. 2. If $g_{\phi _1}(n) \succeq 2^n$ , then $\delta _{M_{\Phi }}(n) \succeq 2^n$ .

Proof. If $g_{\phi _1}^{cyc}(n) \simeq _{\ell } n^{d_1}$ then by Lemma 7.6 (5), $g_{\phi _1^{-1}}^{cyc}(n) \simeq _{\ell } n^{d_1}$ . Let $x \in F_k$ and $C_1\gt 0$ be such that $||\phi _1^{-n}(x)|| \geq C_1n^{d_1}$ for all $n \in \mathbb{N}$ . If $\phi _2$ is polynomially growing, there is $y \in F_l$ and $C_2\gt 0$ such that $||\phi _2^n(y)|| \geq C_2 n^{d_2}$ , and if $\phi _2$ is exponentially growing, choose $y$ such that for some $b_y\gt 1$ , $ ||\phi _2^n(y)|| \succeq{b_y}^n$ . We will present the proof for 1. The algebraic mapping torus $M_{\Phi }$ has presentation:

\begin{equation*}\langle \ a_1, \dots, a_k, \,b_1, \dots, b_l,\, t \mid t^{-1}a_it= \phi _1(a_i), \ t^{-1}b_jt= \phi _2(b_j), \ [a_i, b_j]=1 \ \ \forall i,j \rangle .\end{equation*}

Consider the word $w_n = t^{-4n}y^nt^{4n}x^n t^{-4n} y^{-n}t^{4n}x^{-n}$ .

Suppose $\Delta$ is any van Kampen diagram for $w_n$ . As indicated in Figure 22a, a $t$ -corridor beginning on side 1 can only end on sides 2 or 4. Since $t$ -corridors cannot cross, there is some value $h \in \{0, \dots, 4n\}$ so that the first $h$ $t$ -corridors emanating from side 1 end on side 2 and the remainder end on side 4. This switching point $h$ determines the diagram, as shown in Figure 22b. If $h \geq 2n$ , then a stack of at least $2n$ $t$ -corridors $\mathcal{C}_1, \mathcal{C}_2, \ldots$ (emanating from the 1st, 2nd etc., edge of side 1) start on side 1 and end on side 2. If $h \lt 2n$ , then a stack of at least $2n$ $t$ -corridors start on side 1 and end on side 4: in this case take $\mathcal{C}_1$ to be that emanating from the final edge of side 1, $\mathcal{C}_2$ to be that emanating from the penultimate edge, etc. Let $|\mathcal{C}_i|$ be the area of corridor $\mathcal{C}_i$ , that is, the number of 2-cells in the corridor.

Figure 22. Van Kampen diagrams for $w_n$ in the mapping torus with base $F_k \times F_l$ and automorphism $\phi _1 \times \phi _2$ .

The area of each corridor can be bounded from below by the length of its shortest side, and that can be bounded below by the cyclically reduced length of the shortest side. For $g \in F$ and $n \in \mathbb{N}$ , $||g^n|| = n||g||$ , so we get

\begin{equation*}|\mathcal {C}_i| \ \geq \ \min \{ ||\phi _1^{-i}(x^n)||, ||\phi _2^{i}(y^n)||\} \ = \ \min \{ n||\phi _1^{-i}(x)||, n||\phi _2^{i}(y)||\} \ \geq \ n \min \{C_1i^{d_1}, C_2i^{d_2}\}.\end{equation*}

Summing the areas of corridors $\mathcal{C}_n, \ldots, \mathcal{C}_{2n-1}$ , we find that

(7.1) \begin{equation} \textrm{Area}(\Delta ) \ \geq \ \sum _{i=n}^{2n-1}|\mathcal{C}_i| \ \geq \ n^2\min \{C_1n^{d_1}, C_2n^{d_2}\}. \end{equation}

Now $ |w_n| \leq 16n + 2n|x| + 2n|y|$ . This gives the first of the following inequalities and, as $\Delta$ was any van Kampen diagram for $w_n$ , (7.1) gives the second:

\begin{equation*}\textrm {Area}(16n + 2n|x| + 2n|y|) \ \geq \ \textrm {Area}(w_n) \ \geq \ n^2\min \{C_1n^{d_1}, C_2n^{d_2}\} \ \succeq \ n^{d_1+2}.\end{equation*}

It then follows that $\textrm{Area}(n) \succeq n^{d_1+2}$ , completing our proof of claim 1.

By hypothesis, $g_{\phi _1}(n) \succeq 2^n$ and $g_{\phi _1}^{cyc} \preceq _{\ell } g_{\phi _2}^{cyc}$ . Lemma 7.6 (5) tells us that $g_{\phi _1}^{cyc} \simeq _{\ell } g_{\phi _1^{-1}}^{cyc}$ .

Theorem 3 of [19] bounds growth of elements under an automorphism: for all $\phi \in{\textrm{Aut}}(F_k)$ and all $x \in F_k$ , there exist $C_1$ , $C_2 \gt 0$ , $\lambda \geq 1$ , and $m \in \mathbb{N}$ such that $C_1\lambda ^p p^m\leq |\phi ^p (x)|\leq C_2 \lambda ^p p^m$ for all $p\geq 1$ . (Polynomially growing automorphisms are those with $\lambda =1$ for all $x$ and exponentially growing automorphisms are those with $\lambda \gt 1$ for some $x$ .) Thus, there exist $x\in F_k$ and $y\in F_l$ such that for some $b_1, b_2 \gt 1$ we have that $||\phi _1^{-n}(x)|| \succeq{b_1}^n$ and $||\phi _2^{n}(y)|| \succeq{b_2}^n$ for all $n \geq 1$ . Then, $w_n = t^{-4n}yt^{4n}x t^{-4n} yt^{4n}x$ satisfies $\textrm{Area}(w_n) \succeq \min \{{b_1}^n,{b_2}^n\}$ as any van Kampen diagram for $w_n$ must have a stack of $n$ corridors whose lengths grow either at least like ${b_1}^n$ or ${b_2}^n$ . So, as $\min \{{b_1}^n,{b_2}^n\} \simeq 2^n$ , we conclude that $\textrm{Area}(n) \succeq 2^n$ .

7.4. Dehn function upper bounds

Lemma 7.10. Suppose $\Phi \in{\textrm{Aut}}(F_k \times F_l)$ has the form $\Phi = \phi _1 \times \phi _2$ , where $\phi _1 \in{\textrm{Aut}}(F_k)$ and $\phi _2 \in{\textrm{Aut}}(F_l)$ . If $n^{d_1} \simeq g_{\phi _1}(n) \preceq g_{\phi _2}(n)$ , then $\delta _{M_{\Phi }}(n) \preceq n^{d_1+2}$ . In the case that $\phi _1$ is periodic, $\delta _{M_{\Phi }}(n) \preceq n^{2}$ .

Proof. Suppose $w= w_1 t^{c_1} w_2 t^{c_2} \cdots w_m t^{c_{m}}$ is a length- $n$ word whose subwords $w_i$ are in $\langle a_1, \dots, a_k, b_1, \dots b_l\rangle$ . Suppose that $w=1$ in

\begin{equation*}M_{\Phi } \ = \ \langle a_1, \ldots, a_k, \, b_1, \ldots, b_l, \, t \mid [a_i,b_j]=1, \ t^{-1}a_it= \phi _1(a_i), \ t^{-1}b_jt= \phi _2(b_j), \ \forall i, j \rangle .\end{equation*}

To bound $\delta _{M_{\Phi }}(n)$ from above, we will estimate how many defining relators need to be applied to $w$ to reduce it to the empty word. (We may insert or remove inverse pairs of generators such as $a_i^{-1}a_i$ or $a_ia_i^{-1}$ at no cost. Only applications of defining relators will count toward the estimate.)

By applying fewer than $n^2$ commutators, convert each $w_i$ to $u_iv_i$ for some reduced $u_i \in \langle a_1, \dots, a_k\rangle$ and $v_i \in \langle b_1, \dots, b_l \rangle$ , thereby rewriting $w$ as a word $w^{\prime } = u_1v_1t^{c_1} \dots u_m v_m t^{c_m}$ , which has length at most $n$ .

Next convert $w^{\prime }$ to a product $\overline{v}u$ of the word $\overline{v} = v_1t^{c_1}\cdots v_m t^{c_m}$ with a word $u$ in $\langle a_1, \cdots, a_k\rangle$ , by applying defining relators to shuffle all the $a_1^{\pm 1}, \dots, a_k^{\pm 1}$ in $w'$ to the right. The word $\overline{v}$ represents the identity in $F_l \rtimes _{\phi _2} \langle t \rangle$ and $u$ represents the identity in $F_k$ . Indeed, the index sum of $t$ in $w$ is zero, so gathering all powers of $t$ together on the left would produce a word of the form $vu$ with $u \in F_k$ and $v \in F_l$ which represents the identity in $F_k \times F_l$ , and so $u$ and $v$ freely reduce to the identity—in particular, $\overline{v} = v =1$ in $F_l \rtimes _{\phi _2} \langle t \rangle$ .

This shuffling of $w'$ into $\overline{v}u$ results in the growth of slower growth elements (the $F_k$ factor), but not in growth of faster growth elements (the $F_l$ factor). We can (crudely) estimate cost by giving an upper bound on the length to which a letter $a_i^{\pm 1}$ can grow in the process: it passes at most $n$ letters $t$ or $t^{-1}$ , each time with the effect of applying $\phi _1$ or $\phi _1^{-1}$ . We are given that $n^{d_1} \simeq g_{\phi _1}(n)$ , so $n^{d_1} \simeq g_{\phi ^{-1}_1}(n)$ , by Lemma 7.6 (3). Thus, there is a constant $K\gt 0$ such that $a_i^{\pm 1}$ can grow to length at most $K n^{d_1}$ . The cost to shuffle (and in the process transform) all the (at most $n$ ) letters $a_i^{\pm 1}$ of the $u_1, \ldots, u_m$ to the right past the letters of $\overline{v}$ (of which there are at most $n$ ) is at most $K n^{d_1+2}$ .

Next freely reduce $u$ to the empty word (at no cost to area), leaving the word $\overline{v}$ , which represents the identity in $F_l\rtimes _{\phi _2}\mathbb{Z}$ and has length at most $n$ . By Bridson–Groves [8], $\overline{v}$ can be reduced to the empty word using no more than a constant $c$ times $n^2$ defining relations.

In conclusion, we have an upper bound of $n^2 + K n^{d_1+2} + cn^2$ , which gives that $\delta _{M_{\Phi }}(n) \preceq n^{d_1+2}$ as required.

Finally, we address the periodic case: suppose $l$ is such that $\phi _1^l$ is an inner automorphism. By Lemmas 3.6 and 7.4, $\delta _{M_{\Phi }} \simeq \delta _{M_{\phi _1^l \times \phi _2^l}} \simeq \delta _{M_{\textrm{Id} \times \phi _2^l}} \simeq \delta _{M_{\textrm{Id} \times \phi _2}}$ . We can estimate $\delta _{M_{\textrm{Id} \times \phi _2}}$ by the above argument in the special case that $\phi _1 = \textrm{Id}$ . In this case, the cost of shuffling the $a_i^{\pm 1}$ through the word is at most $n^2$ (rather than $K n^{d_1+2}$ ) since they do not grow in the process, and so $ \delta _{M_{\Phi }}(n) \simeq \delta _{M_{\textrm{Id} \times \phi _2}} (n) \preceq n^2$ .

Proof of Theorem C. We have $G= F_k \times F_l$ , where $k,l \geq 2$ , and $\Psi \in{\textrm{Aut}}(F_k \times F_l)$ . Lemma 7.1 identified a $\Phi = \phi _1 \times \phi _2$ with $\phi _1 \in{\textrm{Aut}}(F_k)$ and $\phi _2 \in{\textrm{Aut}}(F_l)$ which (by Lemma 3.6) has $\delta _{M_{\Psi }} \simeq \delta _{M_{\Phi }}$ .

Provided $\phi _i$ is not periodic, Lemmas 7.7 and 7.8 imply that even if $g_{\phi _i} \not \simeq g^{\text{cyc}}_{\phi _i}$ , there is $\hat{\xi }_i$ such that $g^{\text{cyc}}_{\phi _i} \simeq g_{\hat{\xi }_i} \simeq g^{\text{cyc}}_{\hat{\xi }_i}$ with $M_{\hat{\xi }_1 \times \hat{\xi }_2} \simeq M_{\Phi }$ .

The theorem claims that

1. (1) If $[\phi _1^p] = [\textrm{Id}] \in \textrm{Out}(F_k)$ for some $p \in \mathbb{N}$ (i.e. $\phi _1$ is periodic), then $\delta _{M_{\Psi }}(n) \simeq n^2$ .

2. (2) If $n^{d_1} \simeq g_{\phi _1}^{cyc}(n) \preceq g_{\phi _2}^{cyc}(n)$ , then $\delta _{M_{\Psi }}(n) \simeq n^{d_1+2}$ , and likewise with the indices $1$ and $2$ interchanged.

3. (3) If $g^{cyc}_{\phi _1}(n) \simeq g_{\phi _2}^{cyc}(n) \simeq 2^n$ , then $\delta _{M_{\Psi }}$ grows exponentially.

For (1), Lemma 7.10 gives $\delta _{M_{\Phi }}(n) \preceq n^{2}$ , and we have $\delta _{M_{\Phi }}(n) \succeq n^{2}$ by Lemma 3.4. For (2), Lemma 7.9 gives the required lower bound on the Dehn function and (since $g_{\hat{\xi }_1} \simeq g^{\text{cyc}}_{\phi _1}$ ) Lemma 7.10 gives the upper bound. For (3), Lemma 7.9 again gives the lower bound, and Lemma 3.4 gives the upper bound.

8. Concluding remarks

We finish with some remarks on the limits of our techniques and suggestions for which mapping tori to explore next.

The case $G = F_k \times \mathbb{Z}$ , when $k \geq 3$ , stands in the way of a full classification of Dehn functions of mapping tori over $F_k \times F_l$ . It differs from $F_k \times F_l$ with $k,l\geq 2$ because $F_k\times \mathbb{Z}$ has nontrivial center, which results in additional transvections, making its automorphism group more complicated. What we can say about Dehn functions $\delta$ of mapping tori of $F_k \times \mathbb{Z}$ is that they satisfy $n^2 \preceq \delta (n) \preceq n^3$ . The cubic upper bound comes by recognizing $M_{\Psi }$ as a central extension of $M_{\psi }$ and then applying Corollary 5.3. The quadratic lower bound comes from the presence of a $\mathbb{Z}^2$ -subgroup: the square of the stable letter commutes with the $\mathbb{Z}$ -factor. In special cases, we can determine the Dehn function.

For all $\Psi \in{\textrm{Aut}}(F_k \times \mathbb{Z})$ , there exists $\Phi \in{\textrm{Aut}}(F_k \times \mathbb{Z})$ with the form $\Phi \;:\;x_i \mapsto \phi (x_i)c^{k_i}, \ c \mapsto c,$ such that $[\Psi ^2] = [\Phi ]$ in $\textrm{Out}(F_k \times \mathbb{Z})$ .

1. 1. If $\phi$ is atoroidal, then $M_{\Psi }$ has quadratic Dehn function by Corollary 5.3, because the base of the central extension is hyperbolic and maximal trees have linear diameter.

2. 2. If there is $w \in F_k$ such that $\Phi (w)=wc^k$ , then $M_{\Psi }$ has cubic Dehn function by Lemma 3.5.

Our techniques in Section 5 for $F_2 \times \mathbb{Z}$ do not apply to $F_k \times \mathbb{Z}$ for $k \geq 3$ . We heavily use that $\textrm{Out}(F_2) \cong \textrm{GL}(2, \mathbb{Z})$ and that for any given $\phi \in{\textrm{Aut}}(F_2)$ some iterate $[\phi ]^m$ fixes the conjugacy class $\left [a^{-1}b^{-1}ab\right ]$ , both of which fail in higher rank.

The RAAGs on four generators that are not covered by our theorems are another natural place to continue these investigations—for instance, the RAAG whose defining graph is the path with four vertices and three edges.