Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Higgins, Peter M.
1990.
Lattices, Semigroups, and Universal Algebra.
p.
89.
Araújo, João
and
Konieczny, Janusz
2004.
Semigroups of Transformations Preserving an Equivalence Relation and a Cross-Section.
Communications in Algebra,
Vol. 32,
Issue. 5,
p.
1917.
Konieczny, Janusz
2004.
Semigroups of Transformations Commuting with Injective Nilpotents.
Communications in Algebra,
Vol. 32,
Issue. 4,
p.
1551.
KONIECZNY, JANUSZ
2013.
CENTRALISERS IN THE INFINITE SYMMETRIC INVERSE SEMIGROUP.
Bulletin of the Australian Mathematical Society,
Vol. 87,
Issue. 3,
p.
462.
Araújo, João
and
Konieczny, Janusz
2013.
Centralizers in the Full Transformation Semigroup.
Semigroup Forum,
Vol. 86,
Issue. 1,
p.
1.
Jakubíková-Studenovská, Danica
and
Šuličová, Miroslava
2015.
Centralizers of a monounary algebra.
Asian-European Journal of Mathematics,
Vol. 08,
Issue. 01,
p.
1550007.
Araújo, João
Bentz, Wolfram
and
Konieczny, Janusz
2017.
Directed graphs of inner translations of semigroups.
Semigroup Forum,
Vol. 94,
Issue. 3,
p.
650.
Konieczny, Janusz
2018.
Centralizers of full injective transformations in the symmetric inverse semigroup.
Semigroup Forum,
Vol. 96,
Issue. 3,
p.
474.
Konieczny, Janusz
2020.
Second centralizers in the semigroup of injective transformations.
Asian-European Journal of Mathematics,
Vol. 13,
Issue. 04,
p.
2050069.
Konieczny, Janusz
2020.
The structure of centralizers in the finite symmetric inverse semigroup.
Communications in Algebra,
Vol. 48,
Issue. 12,
p.
5181.

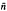 = {1, 2, …
= {1, 2, … 