Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T06:56:18.819Z Has data issue: false hasContentIssue false
  • English
  • Français

DISTAL ACTIONS OF AUTOMORPHISMS OF NILPOTENT GROUPS G ON SUBG AND APPLICATIONS TO LATTICES IN LIE GROUPS

Part of: Lie groups Topological dynamics Locally compact groups and their algebras

Published online by Cambridge University Press:  23 June 2020

RAJDIP PALIT  and
RIDDHI SHAH
RAJDIP PALIT
Affiliation:
School of Physical Sciences, Jawaharlal Nehru University, New Delhi110 067, India, e-mails: rajdip1729@gmail.com; rshah@jnu.ac.in; riddhi.kausti@gmail.com
RIDDHI SHAH
Affiliation:
School of Physical Sciences, Jawaharlal Nehru University, New Delhi110 067, India, e-mails: rajdip1729@gmail.com; rshah@jnu.ac.in; riddhi.kausti@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

For a locally compact group G, we study the distality of the action of automorphisms T of G on SubG, the compact space of closed subgroups of G endowed with the Chabauty topology. For a certain class of discrete groups G, we show that T acts distally on SubG if and only if Tn is the identity map for some 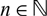$n\in\mathbb N$ . As an application, we get that for a T-invariant lattice Γ in a simply connected nilpotent Lie group G, T acts distally on SubG if and only if it acts distally on SubΓ. This also holds for any closed T-invariant co-compact subgroup Γ in G. For a lattice Γ in a simply connected solvable Lie group, we study conditions under which its automorphisms act distally on SubΓ. We construct an example highlighting the difference between the behaviour of automorphisms on a lattice in a solvable Lie group and that in a nilpotent Lie group. We also characterise automorphisms of a lattice Γ in a connected semisimple Lie group which act distally on SubΓ. For torsion-free compactly generated nilpotent (metrisable) groups G, we obtain the following characterisation: T acts distally on SubG if and only if T is contained in a compact subgroup of Aut(G). Using these results, we characterise the class of such groups G which act distally on SubG. We also show that any compactly generated distal group G is Lie projective.

MSC classification

Primary: 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.)
Secondary: 22E25: Nilpotent and solvable Lie groups 22E40: Discrete subgroups of Lie groups 22D45: Automorphism groups of locally compact groups
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 63 , Issue 2 , May 2021 , pp. 343 - 362
Copyright
© The Author(s), 2020. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abels, H., Distal affine transformation group, J. Reine Angew. Math. 299–300 (1978), 294–300.Google Scholar
Abels, H., Distal automorphism groups of Lie groups, J. Reine Angew. Math. 329 (1981), 82–87.Google Scholar
Arens, R., Topologies for homeomorphism groups, Amer. J. Math. 68 (1946), 593–610.CrossRefGoogle Scholar
Abert, M., Bergeron, N., Biringer, I., Gelander, T., Nikolov, N., Raimbault, J. and Samet, I., On the growth of L 2-invariants for sequences of lattices in Lie groups, Ann. Math. 185(2) (2017), 711–790.CrossRefGoogle Scholar
Baik, H. and Clavier, L., The space of geometric limits of one-generator closed subgroups of ${\rm PSL}_2(\mathbb R)$ , Algebr. Geom. Topol. 13 (2013), 549–576.Google Scholar
Baik, H. and Clavier, L., The space of geometric limits of abelian subgroups of ${\rm PSL}_2(\mathbb C)$ , Hiroshima Math. J. 46 (2016), 1–36.CrossRefGoogle Scholar
Benedetti, R. and Petronio, C., Lectures on hyperbolic geometry (Springer-Verlag, Berlin, 1992).CrossRefGoogle Scholar
Berglund, J. F., Junghenn, H. D. and Milnes, P., Analysis on semigroups. Function spaces, compactifications, representations, Canadian Mathematical Society Series of Monographs and Advanced Texts. A Wiley-Interscience Publication (John Wiley & Sons, Inc., New York, 1989).Google Scholar
Borel, A., Introduction to arithmetic groups, University Lecture Series, vol. 73, (American Mathematical Society, Providence, RI, 2019).CrossRefGoogle Scholar
Bridson, M., de la Harpe, P. and Kleptsyn, V., The Chabauty space of closed subgroups of the three-dimensional Heisenberg group, Pacific J. Math. 240 (2009), 1–48.CrossRefGoogle Scholar
Chabauty, C., Limite d’ensemble et géométrie des nombres, Bull. Soc. Math. France 78 (1950), 143–151.CrossRefGoogle Scholar
Dani, S. G., Convolution roots and embeddings of probability measures on locally compact groups. Indian J. Pure Appl. Math. 41 (2010), 241–250.CrossRefGoogle Scholar
Ellis, R., Distal transformation Groups, Pacific J. Math. 8 (1958) 401–405.CrossRefGoogle Scholar
Furstenberg, H., The Structure of distal flows, Amer. J. Math. 85 (1963), 477–515.Google Scholar
Heyer, H., Probability measures on locally compact groups (Springer-Verlag, Berlin-New York, 1977).Google Scholar
Hochschild, G., The Automorphism group of a Lie group, Trans. Amer. Math. Soc. 72 (1952), 209–216.Google Scholar
Iwasawa, K., On some type of topological groups, Annals of Math. II 50 (1949), 507–558.CrossRefGoogle Scholar
Jaworski, W., Contraction groups, ergodicity and distal properties of automorphisms on compact groups. Illinois J. Math. 56 (2012), 1023–1084.CrossRefGoogle Scholar
Jaworksi, W. and Raja, C. R. E., The Choquet-Deny theorem and distal properties of totally disconnected locally compact groups of polynomial growth, New York J. Math. 13 (2007), 159–174.Google Scholar
Jenkins, J., Growth of connected locally compact groups, J. Functional Analysis 12 (1973), 113–127.CrossRefGoogle Scholar
Losert, V., On the structure of groups with polynomial growth Math. Zeit. 195 (1987), 109–117.Google Scholar
Losert, V., On the structure of groups with polynomial growth II. J. Lond. Math. Soc. 63 (2001), 640–654.CrossRefGoogle Scholar
Moore, C. C., Distal affine transformation groups, Amer. J. Math. 90 (1968), 733–751.CrossRefGoogle Scholar
Pourezza, I. and Hubbard, J., The space of closed subgroups of $\mathbb R^2$ , Topology 18 (1979), 143–146.CrossRefGoogle Scholar
Raghunathan, M. S., Discrete subgroups of Lie groups (Springer-Verlag, New York-Heidelberg, 1972).CrossRefGoogle Scholar
Raja, C. R. E. and Shah, R., Distal actions and shifted convolution property, Israel J. Math. 177 (2010), 301–318.CrossRefGoogle Scholar
Raja, C. R. E. and Shah, R., Some properties of distal actions on locally compact groups, Ergodic Theory Dynam. Syst. 39 (2019), 1340–1360.Google Scholar
Reid, C. D., Dynamics of flat actions on totally disconnected, locally compact groups, New York J. Math. 22 (2016), 115–190.Google Scholar
Rosenblatt, J., A distal property of groups and the growth of connected locally compact groups, Mathematika 26 (1979), 94–98.CrossRefGoogle Scholar
Shah, R., Orbits of distal actions on locally compact groups, J. Lie Theory 22 (2010), 586–599.Google Scholar
Shah, R. and Yadav, A. K., Distality of certain actions on p-adic spheres, J. Australian Math. Soc. doi: 10.1017/S1446788719000272.Google Scholar
Shah, R. and Yadav, A. K., Distal actions of automorphisms of Lie groups G on SubG. arXiv:1909.04397.Google Scholar
Stroppel, M., Locally compact groups, EMS Textbooks in Mathematics (European Mathematical Society, Zürich. 2006).Google Scholar
Willis, G. A., Totally disconnected, nilpotent, locally compact groups, Bull. Austral. Math. Soc. 55 (1997), 143–146.CrossRefGoogle Scholar