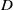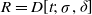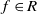1. Introduction
Rank distance codes are important both in coding theory and cryptography. One of the best-known maximum rank distance (MRD) codes is probably the Gabidulin code [Reference Gabidulin10] which was mentioned already by Delsarte [Reference Delsarte8]. In coding theory, MRD codes are well suited to correct errors [Reference Blaum and McEliece6, Reference Roth31]. In cryptography, they are used to design public-key cryptosystems, see for instance [Reference Faure and Loidreau9, Reference Gabidulin, Paramonov and Tretjakov12].
MRD codes over general (non-finite) fields, in particular number fields, were already studied in [Reference Augot, Loidreau and Robert2] and later touched on in [Reference Sheekey34]. Rank metric codes over both cyclic and more general Galois extensions were considered in [Reference Augot, Couvreur, Lavauzelle and Neri3, Reference Roth31, Reference Roth32]. Although rank metric codes have been also constructed over finite principal ideal rings [Reference Kamche and Mouaha19] and discretely valued rings [Reference Maazouz, Hahn, Neri and Stanojkovski21], to our knowledge they have not yet been studied over noncommutative rings. In this paper, we also consider MRD codes in
![]() $M_k(B)$
, where
$M_k(B)$
, where
![]() $B$
is a noncommutative division algebra.
$B$
is a noncommutative division algebra.
We construct these MRD codes using skew polynomials. Skew polynomials have been successfully used in constructions of both division algebras (mostly semifields) and linear codes [Reference Augot, Loidreau and Robert2, Reference Boucher and Ulmer4, Reference Boulagouaz and Leroy5, Reference Fogarty and Gluesing-Luerssen13, Reference Petit26–Reference Pumplün28], in particular building space-time block codes (STBCs) [Reference Pumplün29] and MRD codes [Reference Sheekey33, Reference Sheekey34].
Our codes can be seen as generalizations of both the classical and twisted Gabidulin codes in [Reference Gabidulin10], resp., [Reference Sheekey33]. We put Sheekey’s construction [Reference Sheekey34] in a broader context which helps to understand it better and potentially allows other ways to generalize MRD coding using skew polynomials. The drawback is that rather early on we have to rigorously restrict the choice of the polynomials
![]() $f$
we can employ and that the construction remains rather theoretical.
$f$
we can employ and that the construction remains rather theoretical.
Sheekey [Reference Sheekey34] only considers skew polynomials
![]() $f\in K[t;\;\sigma ]$
with coefficients in cyclic Galois field extensions for his construction and limits himself to the case that the minimal central left multiple of
$f\in K[t;\;\sigma ]$
with coefficients in cyclic Galois field extensions for his construction and limits himself to the case that the minimal central left multiple of
![]() $f$
has maximal degree. He misses out on codes (with matrix entries both in a noncommutative division algebra, and with entries in fields) and algebras that can be obtained by employing skew polynomials with coefficients in a noncommutative division algebra. He also misses out on constructions using
$f$
has maximal degree. He misses out on codes (with matrix entries both in a noncommutative division algebra, and with entries in fields) and algebras that can be obtained by employing skew polynomials with coefficients in a noncommutative division algebra. He also misses out on constructions using
![]() $f\in D[t;\;\delta ]$
. We construct both new division algebras and MRD codes with entries in a noncommutative division algebra, and with entries in fields.
$f\in D[t;\;\delta ]$
. We construct both new division algebras and MRD codes with entries in a noncommutative division algebra, and with entries in fields.
The first five Sections of the paper contain the preliminaries (Section 1) and theoretical background needed to obtain the main results (Sections 2
–5). Let
![]() $D$
be a division algebra of degree
$D$
be a division algebra of degree
![]() $d$
over its center, and
$d$
over its center, and
![]() $f\in R=D[t;\;\sigma,\delta ]$
a monic irreducible skew polynomial with a bound that lies in the center
$f\in R=D[t;\;\sigma,\delta ]$
a monic irreducible skew polynomial with a bound that lies in the center
![]() $C(R)$
of
$C(R)$
of
![]() $R$
.
$R$
.
While developing the theory, we point out how the choice of
![]() $D$
and the polynomial
$D$
and the polynomial
![]() $f$
has to be restricted in order to construct both division algebras and MRD codes out of
$f$
has to be restricted in order to construct both division algebras and MRD codes out of
![]() $f$
, a scalar
$f$
, a scalar
![]() $\nu \in D$
and a suitable
$\nu \in D$
and a suitable
![]() $\rho \in \textrm{Aut}(D)$
.
$\rho \in \textrm{Aut}(D)$
.
Apart from Section 9, we fix the following general assumptions unless specified otherwise:
![]() $R=D[t;\;\sigma ]$
, where
$R=D[t;\;\sigma ]$
, where
![]() $\sigma$
is an automorphism of
$\sigma$
is an automorphism of
![]() $D$
of finite order
$D$
of finite order
![]() $n$
modulo inner automorphisms, i.e.
$n$
modulo inner automorphisms, i.e.
![]() $\sigma ^n=i_u$
for some inner automorphism
$\sigma ^n=i_u$
for some inner automorphism
![]() $i_u(z)=uzu^{-1}$
, and
$i_u(z)=uzu^{-1}$
, and
![]() $F=C\cap \textrm{Fix}(\sigma )$
. Choose
$F=C\cap \textrm{Fix}(\sigma )$
. Choose
![]() $\rho \in \textrm{Aut}(D)$
, such that
$\rho \in \textrm{Aut}(D)$
, such that
![]() $F/F'$
with
$F/F'$
with
![]() $F'=\textrm{Fix}(\rho )\cap F$
is finite-dimensional. Let
$F'=\textrm{Fix}(\rho )\cap F$
is finite-dimensional. Let
![]() $\nu \in D^\times$
.
$\nu \in D^\times$
.
Let
![]() $f\in R$
be monic and irreducible of degree
$f\in R$
be monic and irreducible of degree
![]() $m\gt 1$
, and
$m\gt 1$
, and
![]() $h$
the minimal central left multiple of
$h$
the minimal central left multiple of
![]() $f$
, so that
$f$
, so that
![]() $ R/Rh \cong M_k(B)$
for some division algebra
$ R/Rh \cong M_k(B)$
for some division algebra
![]() $B$
(Theorem 3). Let
$B$
(Theorem 3). Let
![]() $l\lt k$
be a positive integer. Define
$l\lt k$
be a positive integer. Define
![]() $S_{n,m,l}(\nu,\rho, f)=\lbrace a+Rh\,|\, a\in P\rbrace \subset R/Rh$
with the set
$S_{n,m,l}(\nu,\rho, f)=\lbrace a+Rh\,|\, a\in P\rbrace \subset R/Rh$
with the set
![]() $P=\lbrace d_0+d_1t+\dots +d_{lm-1}t^{lm-1}+\nu \rho (d_0)t^{lm}\,|\, d_i\in D\rbrace .$
Let
$P=\lbrace d_0+d_1t+\dots +d_{lm-1}t^{lm-1}+\nu \rho (d_0)t^{lm}\,|\, d_i\in D\rbrace .$
Let
![]() $L_a\;:\;R/Rf\to R/Rf$
be the left multiplication map
$L_a\;:\;R/Rf\to R/Rf$
be the left multiplication map
![]() $L_a(b+Rf)=ab+Rf$
. We have well-defined maps
$L_a(b+Rf)=ab+Rf$
. We have well-defined maps
![]() $ S_{n,m,l}(\nu,\rho, f) \longrightarrow \textrm{End}_B(R/Rf)\longrightarrow M_k(B), a\mapsto L_a \mapsto M_a,$
where
$ S_{n,m,l}(\nu,\rho, f) \longrightarrow \textrm{End}_B(R/Rf)\longrightarrow M_k(B), a\mapsto L_a \mapsto M_a,$
where
![]() $M_a$
is the matrix representing
$M_a$
is the matrix representing
![]() $L_a$
with respect to a right
$L_a$
with respect to a right
![]() $B$
-basis of
$B$
-basis of
![]() $R/Rf$
. The image
$R/Rf$
. The image
![]() $\mathcal{C}_{n,m,l}=\lbrace M_a\mid a\in S_{n,m,l}(\nu,\rho,f)\rbrace$
of
$\mathcal{C}_{n,m,l}=\lbrace M_a\mid a\in S_{n,m,l}(\nu,\rho,f)\rbrace$
of
![]() $S_{n,m,l}(\nu,\rho,h)$
in
$S_{n,m,l}(\nu,\rho,h)$
in
![]() $M_{k}(B)$
is an
$M_{k}(B)$
is an
![]() $F'$
-linear rank metric code. If
$F'$
-linear rank metric code. If
![]() $\mathcal{C}_{n,m,l}$
has distance
$\mathcal{C}_{n,m,l}$
has distance
![]() $d_{\mathcal{C}}=k-l+1$
, then
$d_{\mathcal{C}}=k-l+1$
, then
![]() $\mathcal{C}_{n,m,l}$
is called a maximum rank distance code in
$\mathcal{C}_{n,m,l}$
is called a maximum rank distance code in
![]() $M_k(B)$
. We will usually deal with the case that
$M_k(B)$
. We will usually deal with the case that
![]() $deg (h)=dmn$
, so that
$deg (h)=dmn$
, so that
![]() $B$
is a field.
$B$
is a field.
The most general results are contained in Section 6: If
![]() $P$
does not contain a polynomial of degree
$P$
does not contain a polynomial of degree
![]() $lm$
, whose irreducible factors are all similar to
$lm$
, whose irreducible factors are all similar to
![]() $f$
, then
$f$
, then
![]() $\mathcal{C}_{n,m,l}$
is an
$\mathcal{C}_{n,m,l}$
is an
![]() $F'$
-linear MRD code in
$F'$
-linear MRD code in
![]() $M_k(B)$
with minimum distance
$M_k(B)$
with minimum distance
![]() $k-l+1$
(Theorem 19).
$k-l+1$
(Theorem 19).
Furthermore, let
![]() $D=(E/C,\gamma,a)$
be a cyclic division algebra such that
$D=(E/C,\gamma,a)$
be a cyclic division algebra such that
![]() $\sigma |_E\in \textrm{Aut}(E)$
and
$\sigma |_E\in \textrm{Aut}(E)$
and
![]() $\gamma \circ \sigma |_E=\sigma |_E\circ \gamma$
, and
$\gamma \circ \sigma |_E=\sigma |_E\circ \gamma$
, and
![]() $\sigma ^n(z)=u^{-1}zu$
for some
$\sigma ^n(z)=u^{-1}zu$
for some
![]() $u\in E$
. Let
$u\in E$
. Let
![]() $f(t)=\sum _{i=0}^ma_it^i\in E[t;\;\sigma ]$
be a monic irreducible polynomial of degree
$f(t)=\sum _{i=0}^ma_it^i\in E[t;\;\sigma ]$
be a monic irreducible polynomial of degree
![]() $m$
, such that
$m$
, such that
![]() $\textrm{deg}(h)=dmn$
, and such that all monic
$\textrm{deg}(h)=dmn$
, and such that all monic
![]() $f_i$
similar to
$f_i$
similar to
![]() $f$
lie in
$f$
lie in
![]() $E[t;\;\sigma ]$
. Then, the algebra
$E[t;\;\sigma ]$
. Then, the algebra
![]() $S_{n,m,1}(\nu,\rho, f)$
is a division algebra, if one of the following holds: (i)
$S_{n,m,1}(\nu,\rho, f)$
is a division algebra, if one of the following holds: (i)
![]() $\nu \not \in E$
and
$\nu \not \in E$
and
![]() $\rho |_E\in \textrm{Aut}(E)$
; (ii)
$\rho |_E\in \textrm{Aut}(E)$
; (ii)
![]() $\nu \in E^\times$
and
$\nu \in E^\times$
and
![]() $\rho |_E\in \textrm{Aut}(E)$
, such that
$\rho |_E\in \textrm{Aut}(E)$
, such that
![]() $N_{E/F'}(a_0) N_{E/F'}(\nu )\neq 1$
(Theorem 16). MRD codes are canonically obtained from the matrices representing the left multiplication of these division algebras.
$N_{E/F'}(a_0) N_{E/F'}(\nu )\neq 1$
(Theorem 16). MRD codes are canonically obtained from the matrices representing the left multiplication of these division algebras.
In Section 7, the nuclei of the algebras and codes are investigated. We give some examples of algebras obtained from our construction employing
![]() $f(t)=t^n-\theta \in K[t;\;\sigma ]$
in Section 8.
$f(t)=t^n-\theta \in K[t;\;\sigma ]$
in Section 8.
We conclude with a brief look at the constructions using a differential polynomial
![]() $f\in D[t;\;\delta ]$
, where the center of
$f\in D[t;\;\delta ]$
, where the center of
![]() $D$
is a field of characteristic
$D$
is a field of characteristic
![]() $p$
, in Section 9.
$p$
, in Section 9.
The fact that we are using
![]() $f\in D[t;\;\sigma ]$
, respectively
$f\in D[t;\;\sigma ]$
, respectively
![]() $f\in D[t;\;\gamma ]$
, means we have a larger choice of skew polynomials to build codes that Sheekey does, who only considers
$f\in D[t;\;\gamma ]$
, means we have a larger choice of skew polynomials to build codes that Sheekey does, who only considers
![]() $f$
with coefficients in a cyclic field extension.
$f$
with coefficients in a cyclic field extension.
This work is part of the second author’s PhD thesis [Reference Thompson35].
2. Preliminaries
2.1. Nonassociative algebras
Let
![]() $F$
be a field. We call
$F$
be a field. We call
![]() $A$
an algebra over
$A$
an algebra over
![]() $F$
if there exists an
$F$
if there exists an
![]() $F$
-bilinear map
$F$
-bilinear map
![]() $A\times A\to A$
,
$A\times A\to A$
,
![]() $(x,y) \mapsto x \cdot y$
, denoted simply by juxtaposition
$(x,y) \mapsto x \cdot y$
, denoted simply by juxtaposition
![]() $xy$
, the multiplication of
$xy$
, the multiplication of
![]() $A$
. An algebra
$A$
. An algebra
![]() $A$
is called unital if there is an element in
$A$
is called unital if there is an element in
![]() $A$
, denoted by 1, such that
$A$
, denoted by 1, such that
![]() $1x=x1=x$
for all
$1x=x1=x$
for all
![]() $x\in A$
. We will only consider unital algebras. A nonassociative algebra
$x\in A$
. We will only consider unital algebras. A nonassociative algebra
![]() $A\not =0$
is called a division algebra if for any
$A\not =0$
is called a division algebra if for any
![]() $a\in A$
,
$a\in A$
,
![]() $a\not =0$
, the left multiplication with
$a\not =0$
, the left multiplication with
![]() $a$
,
$a$
,
![]() $L_a(x)=ax$
, and the right multiplication with
$L_a(x)=ax$
, and the right multiplication with
![]() $a$
,
$a$
,
![]() $R_a(x)=xa$
, are bijective. If
$R_a(x)=xa$
, are bijective. If
![]() $A$
is finite-dimensional as an
$A$
is finite-dimensional as an
![]() $F$
-vector space, then
$F$
-vector space, then
![]() $A$
is a division algebra if and only if
$A$
is a division algebra if and only if
![]() $A$
has no zero divisors. The left nucleus of
$A$
has no zero divisors. The left nucleus of
![]() $A$
is defined as
$A$
is defined as
![]() ${\rm Nuc}_l(A) = \{ x \in A \, \vert \, [x, A, A] = 0 \}$
, the middle nucleus of
${\rm Nuc}_l(A) = \{ x \in A \, \vert \, [x, A, A] = 0 \}$
, the middle nucleus of
![]() $A$
is
$A$
is
![]() $\textrm{Nuc}_m(A) = \{ x \in A \, \vert \, [A, x, A] = 0 \}$
, and the right nucleus of
$\textrm{Nuc}_m(A) = \{ x \in A \, \vert \, [A, x, A] = 0 \}$
, and the right nucleus of
![]() $A$
is
$A$
is
![]() $\textrm{Nuc}_r(A) = \{ x \in A \, \vert \, [A,A, x] = 0 \}$
, where
$\textrm{Nuc}_r(A) = \{ x \in A \, \vert \, [A,A, x] = 0 \}$
, where
![]() $[x, y, z] = (xy) z - x (yz)$
is the associator.
$[x, y, z] = (xy) z - x (yz)$
is the associator.
![]() $\textrm{Nuc}_l(A)$
,
$\textrm{Nuc}_l(A)$
,
![]() $\textrm{Nuc}_m(A)$
, and
$\textrm{Nuc}_m(A)$
, and
![]() $\textrm{Nuc}_r(A)$
are associative subalgebras of
$\textrm{Nuc}_r(A)$
are associative subalgebras of
![]() $A$
. Their intersection
$A$
. Their intersection
![]() $\textrm{Nuc}(A) = \{ x \in A \, \vert \, [x, A, A] = [A, x, A] = [A,A, x] = 0 \}$
is the nucleus of
$\textrm{Nuc}(A) = \{ x \in A \, \vert \, [x, A, A] = [A, x, A] = [A,A, x] = 0 \}$
is the nucleus of
![]() $A$
.
$A$
.
![]() $\textrm{Nuc}(A)$
is an associative subalgebra of
$\textrm{Nuc}(A)$
is an associative subalgebra of
![]() $A$
, and
$A$
, and
![]() $x(yz) = (xy) z$
whenever one of the elements
$x(yz) = (xy) z$
whenever one of the elements
![]() $x, y, z$
is in
$x, y, z$
is in
![]() $\textrm{Nuc}(A)$
. The center of
$\textrm{Nuc}(A)$
. The center of
![]() $A$
is
$A$
is
![]() $\textrm{C}(A)=\{x\in \text{Nuc}(A)\,|\, xy=yx \text{ for all }y\in A\}$
.
$\textrm{C}(A)=\{x\in \text{Nuc}(A)\,|\, xy=yx \text{ for all }y\in A\}$
.
Let
![]() $A$
be a finite-dimensional central simple associative algebra over
$A$
be a finite-dimensional central simple associative algebra over
![]() $F$
of degree
$F$
of degree
![]() $d$
and let
$d$
and let
![]() $\overline{F}$
denote the algebraic closure of
$\overline{F}$
denote the algebraic closure of
![]() $F$
. Then,
$F$
. Then,
![]() $A\otimes _F \overline{F} \cong M_d(\overline{F})$
, so that we can fix an embedding
$A\otimes _F \overline{F} \cong M_d(\overline{F})$
, so that we can fix an embedding
![]() $A \longrightarrow M_d(\overline{F})$
and view every
$A \longrightarrow M_d(\overline{F})$
and view every
![]() $a\in A$
as a matrix in
$a\in A$
as a matrix in
![]() $M_d(\overline{F})$
. The characteristic polynomial
$M_d(\overline{F})$
. The characteristic polynomial
of
![]() $a\in A$
has coefficients in
$a\in A$
has coefficients in
![]() $F$
and is independent of the choice of the embedding. The coefficient
$F$
and is independent of the choice of the embedding. The coefficient
![]() $N_A(a)=s_d(a)$
is called the reduced norm of
$N_A(a)=s_d(a)$
is called the reduced norm of
![]() $a$
[Reference Knus, Merkurjev, Rost and Tignol20]. Let
$a$
[Reference Knus, Merkurjev, Rost and Tignol20]. Let
![]() $K/F$
be a cyclic Galois extension of degree
$K/F$
be a cyclic Galois extension of degree
![]() $d$
with Galois group
$d$
with Galois group
![]() $\textrm{Gal}(K/F)=\langle \gamma \rangle$
and norm
$\textrm{Gal}(K/F)=\langle \gamma \rangle$
and norm
![]() $N_{K/F}$
. Let
$N_{K/F}$
. Let
![]() $c\in F^\times$
. An associative cyclic algebra
$c\in F^\times$
. An associative cyclic algebra
![]() $(K/F,\gamma,c)$
of degree
$(K/F,\gamma,c)$
of degree
![]() $d$
over
$d$
over
![]() $F$
is a
$F$
is a
![]() $d$
-dimensional
$d$
-dimensional
![]() $K$
-vector space
$K$
-vector space
with multiplication given by the relations
![]() $ e^d=c,\,le=e\sigma (l),$
for all
$ e^d=c,\,le=e\sigma (l),$
for all
![]() $l\in K$
.
$l\in K$
.
![]() $(K/F,\gamma,c)$
is a division algebra for all
$(K/F,\gamma,c)$
is a division algebra for all
![]() $c\in F^\times$
, such that
$c\in F^\times$
, such that
![]() $c^s\not \in N_{K/F}(K^\times )$
for all
$c^s\not \in N_{K/F}(K^\times )$
for all
![]() $s$
which are prime divisors of
$s$
which are prime divisors of
![]() $d$
,
$d$
,
![]() $1\leq s\leq d-1$
.
$1\leq s\leq d-1$
.
2.2. MRD codes
Let
![]() $K$
be a field. A code is a set of matrices
$K$
be a field. A code is a set of matrices
![]() $\mathcal{C}\subset M_{n, m}(K)$
. Let
$\mathcal{C}\subset M_{n, m}(K)$
. Let
![]() $L\subset K$
be a subfield, then
$L\subset K$
be a subfield, then
![]() $\mathcal{C}$
is
$\mathcal{C}$
is
![]() $L$
-linear if
$L$
-linear if
![]() $\mathcal{C}$
is a vector space over
$\mathcal{C}$
is a vector space over
![]() $L$
. A rank metric code is a code
$L$
. A rank metric code is a code
![]() $\mathcal{C}\subset M_{n, m}(K)$
equipped with the rank distance function
$\mathcal{C}\subset M_{n, m}(K)$
equipped with the rank distance function
![]() $d(X,Y)=\textrm{rank}(X-Y).$
Define the minimum distance of a rank metric code
$d(X,Y)=\textrm{rank}(X-Y).$
Define the minimum distance of a rank metric code
![]() $\mathcal{C}$
as
$\mathcal{C}$
as
An
![]() $L$
-linear rank metric code
$L$
-linear rank metric code
![]() $\mathcal{C}$
satisfies the Singleton-like bound
$\mathcal{C}$
satisfies the Singleton-like bound
where
![]() $\text{dim}_L(\mathcal{C})$
is the dimension of the
$\text{dim}_L(\mathcal{C})$
is the dimension of the
![]() $L$
-vector space
$L$
-vector space
![]() $\mathcal{C}$
[Reference Augot, Loidreau and Robert2, Proposition 6].
$\mathcal{C}$
[Reference Augot, Loidreau and Robert2, Proposition 6].
An
![]() $L$
-linear rank metric code attaining the Singleton-like bound is called a maximum rank distance code or MRD code (for MRD codes over cyclic field extensions see [Reference Augot, Loidreau and Robert2]).
$L$
-linear rank metric code attaining the Singleton-like bound is called a maximum rank distance code or MRD code (for MRD codes over cyclic field extensions see [Reference Augot, Loidreau and Robert2]).
If now
![]() $B$
is a not necessarily commutative division algebra then more generally, we again define a code as a set of matrices
$B$
is a not necessarily commutative division algebra then more generally, we again define a code as a set of matrices
![]() $\mathcal{C}\subset M_{n, m}(B)$
. Let
$\mathcal{C}\subset M_{n, m}(B)$
. Let
![]() $B'\subset B$
be a subalgebra, then
$B'\subset B$
be a subalgebra, then
![]() $\mathcal{C}$
is
$\mathcal{C}$
is
![]() $B'$
-linear (or simply linear), if
$B'$
-linear (or simply linear), if
![]() $\mathcal{C}$
is a right
$\mathcal{C}$
is a right
![]() $B'$
-module.
$B'$
-module.
A rank metric code
![]() $\mathcal{C}\subset M_{n, m}(B)$
is a code together with the distance function
$\mathcal{C}\subset M_{n, m}(B)$
is a code together with the distance function
for all
![]() $X,Y\in M_{n,m}(B)$
, where
$X,Y\in M_{n,m}(B)$
, where
![]() $\textrm{colrank}$
is the column rank of
$\textrm{colrank}$
is the column rank of
![]() $A$
(the rank of the right
$A$
(the rank of the right
![]() $B$
-module generated by the columns of
$B$
-module generated by the columns of
![]() $A$
). A matrix in
$A$
). A matrix in
![]() $M_{n,m}(B)$
has column rank at most
$M_{n,m}(B)$
has column rank at most
![]() $m$
; any matrix which attains this bound is said to have attained full column rank. The minimum distance of a rank metric code
$m$
; any matrix which attains this bound is said to have attained full column rank. The minimum distance of a rank metric code
![]() $\mathcal{C}\subset M_{n,m}(B)$
is defined as
$\mathcal{C}\subset M_{n,m}(B)$
is defined as
To our knowledge, such codes
![]() $\mathcal{C}\subset M_{n, m}(B)$
have not previously been considered in the literature.
$\mathcal{C}\subset M_{n, m}(B)$
have not previously been considered in the literature.
2.3. Skew polynomial rings
In the following, let
![]() $D$
be a central simple division algebra of degree
$D$
be a central simple division algebra of degree
![]() $d$
over its center
$d$
over its center
![]() $C$
,
$C$
,
![]() $\sigma$
a ring endomorphism of
$\sigma$
a ring endomorphism of
![]() $D$
and
$D$
and
![]() $\delta\;:\;D\rightarrow D$
a left
$\delta\;:\;D\rightarrow D$
a left
![]() $\sigma$
-derivation, i.e. an additive map such that
$\sigma$
-derivation, i.e. an additive map such that
![]() $\delta (ab)=\sigma (a)\delta (b)+\delta (a)b$
for all
$\delta (ab)=\sigma (a)\delta (b)+\delta (a)b$
for all
![]() $a,b\in D$
. The skew polynomial ring
$a,b\in D$
. The skew polynomial ring
![]() $D[t;\;\sigma,\delta ]$
is the set of skew polynomials
$D[t;\;\sigma,\delta ]$
is the set of skew polynomials
![]() $g(t)=a_0+a_1t+\dots +a_nt^n$
with
$g(t)=a_0+a_1t+\dots +a_nt^n$
with
![]() $a_i\in D$
, with term-wise addition and multiplication defined via
$a_i\in D$
, with term-wise addition and multiplication defined via
![]() $ta=\sigma (a)t+\delta (a)$
for all
$ta=\sigma (a)t+\delta (a)$
for all
![]() $a\in D$
[Reference Ore22]. Define
$a\in D$
[Reference Ore22]. Define
![]() $\textrm{Fix}(\sigma )=\{a\in D\,|\, \sigma (a)=a\}$
and
$\textrm{Fix}(\sigma )=\{a\in D\,|\, \sigma (a)=a\}$
and
![]() $\textrm{Const}(\delta )=\{a\in D\,|\, \delta (a)=0\}$
. If
$\textrm{Const}(\delta )=\{a\in D\,|\, \delta (a)=0\}$
. If
![]() $\delta =0$
, define
$\delta =0$
, define
![]() $D[t;\;\sigma ]=D[t;\;\sigma,0]$
. If
$D[t;\;\sigma ]=D[t;\;\sigma,0]$
. If
![]() $\sigma =id$
, define
$\sigma =id$
, define
![]() $D[t;\;\delta ]=D[t;\;id,\delta ]$
.
$D[t;\;\delta ]=D[t;\;id,\delta ]$
.
For
![]() $f(t)=a_0+a_1t+\dots +a_nt^n\in R=D[t;\;\sigma,\delta ]$
with
$f(t)=a_0+a_1t+\dots +a_nt^n\in R=D[t;\;\sigma,\delta ]$
with
![]() $a_n\not =0$
, we define the degree of
$a_n\not =0$
, we define the degree of
![]() $f$
as
$f$
as
![]() $ \textrm{deg}(f)=n$
and
$ \textrm{deg}(f)=n$
and
![]() $\textrm{deg}(0)=-\infty$
. A skew polynomial
$\textrm{deg}(0)=-\infty$
. A skew polynomial
![]() $f\in R$
is irreducible if it is not a unit and it has no proper factors, i.e if there do not exist
$f\in R$
is irreducible if it is not a unit and it has no proper factors, i.e if there do not exist
![]() $g,h\in R$
with
$g,h\in R$
with
![]() $1\leq \textrm{deg}(g), \textrm{deg }(h)\lt \textrm{deg}(f)$
such that
$1\leq \textrm{deg}(g), \textrm{deg }(h)\lt \textrm{deg}(f)$
such that
![]() $f=gh$
[Reference Jacobson18, p. 2 ff.]. We call
$f=gh$
[Reference Jacobson18, p. 2 ff.]. We call
![]() $f\in R$
right-invariant if
$f\in R$
right-invariant if
![]() $Rf$
is a left and a right ideal in
$Rf$
is a left and a right ideal in
![]() $R$
, and a two-sided maximal element, if
$R$
, and a two-sided maximal element, if
![]() $f$
is right-invariant and
$f$
is right-invariant and
![]() $Rf$
is a nonzero maximal ideal in
$Rf$
is a nonzero maximal ideal in
![]() $R$
(equivalently, if
$R$
(equivalently, if
![]() $f\not =0$
and
$f\not =0$
and
![]() $R/Rf$
is a simple ring) [Reference Jacobson18, p. 13]. Two nonzero skew polynomials
$R/Rf$
is a simple ring) [Reference Jacobson18, p. 13]. Two nonzero skew polynomials
![]() $f_1,f_2 \in R$
are similar, written
$f_1,f_2 \in R$
are similar, written
![]() $f_1\sim f_2$
, if
$f_1\sim f_2$
, if
![]() $R/Rf_1 \cong R/Rf_2$
[Reference Jacobson18, p. 11].
$R/Rf_1 \cong R/Rf_2$
[Reference Jacobson18, p. 11].
A skew polynomial
![]() $f \in R$
is bounded if there exists a nonzero polynomial
$f \in R$
is bounded if there exists a nonzero polynomial
![]() $f^* \in R$
such that
$f^* \in R$
such that
![]() $Rf^*$
is the largest two-sided ideal of
$Rf^*$
is the largest two-sided ideal of
![]() $R$
contained in
$R$
contained in
![]() $Rf$
. The polynomial
$Rf$
. The polynomial
![]() $f^*$
is uniquely determined by
$f^*$
is uniquely determined by
![]() $f$
up to scalar multiplication by elements of
$f$
up to scalar multiplication by elements of
![]() $D^\times$
and is called a bound of
$D^\times$
and is called a bound of
![]() $f$
.
$f$
.
If
![]() $f\in R$
has degree
$f\in R$
has degree
![]() $m$
, then for all
$m$
, then for all
![]() $g\in R$
of degree
$g\in R$
of degree
![]() $l\geq m$
, there exist uniquely determined
$l\geq m$
, there exist uniquely determined
![]() $r,q\in R$
with
$r,q\in R$
with
![]() $\textrm{deg}(r)\lt \textrm{deg}(f)$
, such that
$\textrm{deg}(r)\lt \textrm{deg}(f)$
, such that
![]() $g=qf+r.$
Let
$g=qf+r.$
Let
![]() $\textrm{mod}_r f$
denote the remainder of right division by
$\textrm{mod}_r f$
denote the remainder of right division by
![]() $f$
. The skew polynomials
$f$
. The skew polynomials
![]() $R_m=\{g\in R\,|\, \textrm{deg}(g)\lt m\}$
of degree less that
$R_m=\{g\in R\,|\, \textrm{deg}(g)\lt m\}$
of degree less that
![]() $m$
canonically represent the elements of the left
$m$
canonically represent the elements of the left
![]() $R$
-modules
$R$
-modules
![]() $R/Rf$
. Furthermore,
$R/Rf$
. Furthermore,
![]() $R_m$
together with the multiplication
$R_m$
together with the multiplication
![]() $g\circ h=gh \, \textrm{mod}_r f$
is a unital nonassociative algebra
$g\circ h=gh \, \textrm{mod}_r f$
is a unital nonassociative algebra
![]() $S_f=(R_m,\circ )$
over
$S_f=(R_m,\circ )$
over
![]() $F_0=\{a\in D\,|\, ah=ha \text{ for all } h\in S_f\}=\textrm{Comm}(S_f)\cap D$
, called a Petit algebra. When the context is clear, we simply use juxtaposition for multiplication in
$F_0=\{a\in D\,|\, ah=ha \text{ for all } h\in S_f\}=\textrm{Comm}(S_f)\cap D$
, called a Petit algebra. When the context is clear, we simply use juxtaposition for multiplication in
![]() $S_f$
. Note that
$S_f$
. Note that
![]() $ C(D)\cap \textrm{Fix}(\sigma )\cap \textrm{Const}(\delta )\subset F_0.$
For all
$ C(D)\cap \textrm{Fix}(\sigma )\cap \textrm{Const}(\delta )\subset F_0.$
For all
![]() $a\in D^\times$
, we have
$a\in D^\times$
, we have
![]() $S_f = S_{af}$
; thus, without loss of generality we can assume
$S_f = S_{af}$
; thus, without loss of generality we can assume
![]() $f$
is monic when working with Petit algebras
$f$
is monic when working with Petit algebras
![]() $S_f$
. If
$S_f$
. If
![]() $f$
has degree 1 then
$f$
has degree 1 then
![]() $S_f\cong D$
.
$S_f\cong D$
.
Lemma 1.
Let
![]() $R$
be a ring with no zero divisors. For all
$R$
be a ring with no zero divisors. For all
![]() $g\in C(R)$
, every right divisor of
$g\in C(R)$
, every right divisor of
![]() $g$
in
$g$
in
![]() $R$
also divides
$R$
also divides
![]() $g$
on the left.
$g$
on the left.
Proof. Suppose
![]() $\gamma$
is a right divisor of
$\gamma$
is a right divisor of
![]() $g$
. Then,
$g$
. Then,
![]() $g=\delta \gamma$
for some
$g=\delta \gamma$
for some
![]() $\delta \in R$
. As
$\delta \in R$
. As
![]() $g$
lies in the center of
$g$
lies in the center of
![]() $R$
, we have
$R$
, we have
![]() $\delta g = g\delta =\delta \gamma \delta$
. This rearranges to
$\delta g = g\delta =\delta \gamma \delta$
. This rearranges to
![]() $0=\delta g-\delta \gamma \delta =\delta (g-\gamma \delta ).$
As
$0=\delta g-\delta \gamma \delta =\delta (g-\gamma \delta ).$
As
![]() $R$
contains no zero divisors and
$R$
contains no zero divisors and
![]() $\delta \neq 0$
, it follows that
$\delta \neq 0$
, it follows that
![]() $g=\gamma \delta$
.
$g=\gamma \delta$
.
2.4. The minimal central left multiple of f
 $\boldsymbol\in$
D[t;
$\boldsymbol\in$
D[t;
 $\boldsymbol\sigma$
]
$\boldsymbol\sigma$
]
From now on let,
![]() $\sigma$
be an automorphism of
$\sigma$
be an automorphism of
![]() $D$
of finite order
$D$
of finite order
![]() $n$
modulo inner automorphisms, i.e.
$n$
modulo inner automorphisms, i.e.
![]() $\sigma ^n=i_u$
for some inner automorphism
$\sigma ^n=i_u$
for some inner automorphism
![]() $i_u(z)=uzu^{-1}$
. Then, the order of
$i_u(z)=uzu^{-1}$
. Then, the order of
![]() $\sigma |_C$
is
$\sigma |_C$
is
![]() $n$
. W.l.o.g., we choose
$n$
. W.l.o.g., we choose
![]() $u\in \textrm{Fix}(\sigma )$
. Let
$u\in \textrm{Fix}(\sigma )$
. Let
![]() $R=D[t;\;\sigma ]$
and define
$R=D[t;\;\sigma ]$
and define
![]() $F=C\cap \textrm{Fix}(\sigma )$
.
$F=C\cap \textrm{Fix}(\sigma )$
.
![]() $R$
has center
$R$
has center
 \begin{equation*}C(R) = F[u^{-1}t^n]=\left\{\sum _{i=0}^{k}a_i(u^{-1}t^n)^i\,|\, a_i\in F \right\}\cong F[x]\end{equation*}
\begin{equation*}C(R) = F[u^{-1}t^n]=\left\{\sum _{i=0}^{k}a_i(u^{-1}t^n)^i\,|\, a_i\in F \right\}\cong F[x]\end{equation*}
with
![]() $x=u^{-1}t^n$
[Reference Jacobson18, Theorem 1.1.22]. All polynomials
$x=u^{-1}t^n$
[Reference Jacobson18, Theorem 1.1.22]. All polynomials
![]() $f\in R$
are bounded.
$f\in R$
are bounded.
For any
![]() $f \in R=D[t;\;\sigma ]$
with a bound in
$f \in R=D[t;\;\sigma ]$
with a bound in
![]() $C(R)$
, we define the minimal central left multiple
$C(R)$
, we define the minimal central left multiple
![]() $mclm(f)$
of
$mclm(f)$
of
![]() $f$
in
$f$
in
![]() $R$
to be the unique polynomial of minimal degree
$R$
to be the unique polynomial of minimal degree
![]() $h \in C(R)=F[u^{-1}t^n]$
such that
$h \in C(R)=F[u^{-1}t^n]$
such that
![]() $h = gf$
for some
$h = gf$
for some
![]() $g \in R$
, and such that
$g \in R$
, and such that
![]() $h(t)=\hat{h}(u^{-1}t^n)$
for some monic
$h(t)=\hat{h}(u^{-1}t^n)$
for some monic
![]() $\hat{h}(x) \in F[x]$
. Define
$\hat{h}(x) \in F[x]$
. Define
![]() $E_{\hat{h}}=F[x]/(\hat{h}(x))$
. If
$E_{\hat{h}}=F[x]/(\hat{h}(x))$
. If
![]() $f$
has nonzero constant term, then
$f$
has nonzero constant term, then
![]() $f^*\in C(R)$
[Reference Gòmez-Torrecillas, Lobillo and Navarro11, Lemma 2.11]). From now on, we assume that
$f^*\in C(R)$
[Reference Gòmez-Torrecillas, Lobillo and Navarro11, Lemma 2.11]). From now on, we assume that
![]() $f$
has nonzero constant term and denote by
$f$
has nonzero constant term and denote by
![]() $h \in C(R)$
,
$h \in C(R)$
,
![]() $h(t)=\hat{h}(u^{-1}t^n)$
, the minimal central left multiple of
$h(t)=\hat{h}(u^{-1}t^n)$
, the minimal central left multiple of
![]() $f$
. Then,
$f$
. Then,
![]() $h$
equals the bound of
$h$
equals the bound of
![]() $f$
up to a scalar multiple from
$f$
up to a scalar multiple from
![]() $D$
. If
$D$
. If
![]() $f$
is irreducible in
$f$
is irreducible in
![]() $R$
, then
$R$
, then
![]() $\hat{h}(x)$
is irreducible in
$\hat{h}(x)$
is irreducible in
![]() $F[x]$
. If
$F[x]$
. If
![]() $\hat{h}\in F[x]$
is irreducible, then
$\hat{h}\in F[x]$
is irreducible, then
![]() $f=f_1\cdots f_r$
for irreducible
$f=f_1\cdots f_r$
for irreducible
![]() $f_i\in R$
such that
$f_i\in R$
such that
![]() $f_i\sim f_j$
for all
$f_i\sim f_j$
for all
![]() $i,j$
([Reference Owen23], cf. [Reference Thompson and Pumplün36]).
$i,j$
([Reference Owen23], cf. [Reference Thompson and Pumplün36]).
Lemma 2.
Let
![]() $f\in R$
.
$f\in R$
.
-
(i) If
 $f\in R$
is irreducible, then every
$f\in R$
is irreducible, then every
 $g\in R$
similar to
$g\in R$
similar to
 $f$
has
$f$
has
 $h$
as its minimal central left multiple.
$h$
as its minimal central left multiple.
-
(ii) Suppose that
 $\hat{h}\in F[x]$
is irreducible. Then,
$\hat{h}\in F[x]$
is irreducible. Then,
 $f=f_1\cdots f_r$
for irreducible
$f=f_1\cdots f_r$
for irreducible
 $f_i\in R$
such that
$f_i\in R$
such that
 $f_i\sim f_j$
for all
$f_i\sim f_j$
for all
 $i,j$
.
$i,j$
.
This follows easily from [Reference Carcanague7, p. 9, Corollary 2] and [Reference Jacobson18, Theorem 1.2.9].
The quotient algebra
![]() $ R/Rh$
has center
$ R/Rh$
has center
![]() $ C(R/Rh)\cong F[x]/ (\hat{h}(x) )$
, cf. [Reference Gòmez-Torrecillas, Lobillo and Navarro11, Lemma 4.2]. Define
$ C(R/Rh)\cong F[x]/ (\hat{h}(x) )$
, cf. [Reference Gòmez-Torrecillas, Lobillo and Navarro11, Lemma 4.2]. Define
![]() $E_{\hat{h}}=F[x]/ (\hat{h}(x) )$
. Suppose that
$E_{\hat{h}}=F[x]/ (\hat{h}(x) )$
. Suppose that
![]() $\hat{h}(x) \neq x$
and that
$\hat{h}(x) \neq x$
and that
![]() $\hat{h}$
is irreducible in
$\hat{h}$
is irreducible in
![]() $F[x]$
. Then,
$F[x]$
. Then,
![]() $h$
generates a maximal two-sided ideal
$h$
generates a maximal two-sided ideal
![]() $Rh$
in
$Rh$
in
![]() $R$
[Reference Jacobson18, p. 16] and
$R$
[Reference Jacobson18, p. 16] and
![]() $R/Rh$
is simple over its center
$R/Rh$
is simple over its center
![]() $ E_{\hat{h}}$
.
$ E_{\hat{h}}$
.
Theorem 3 [Reference Owen23]. Let
![]() $f \in R=D[t;\;\sigma ]$
be monic and irreducible of degree
$f \in R=D[t;\;\sigma ]$
be monic and irreducible of degree
![]() $m\gt 1$
with minimal central left multiple
$m\gt 1$
with minimal central left multiple
![]() $h(t)=\hat{h}(u^{-1}t^n)$
. Then,,
$h(t)=\hat{h}(u^{-1}t^n)$
. Then,,
![]() $\textrm{Nuc}_r(S_f)$
is a central division algebra over
$\textrm{Nuc}_r(S_f)$
is a central division algebra over
![]() $E_{\hat{h}}$
of degree
$E_{\hat{h}}$
of degree
![]() $s=dn/k$
, where
$s=dn/k$
, where
![]() $k$
is the number of irreducible factors of
$k$
is the number of irreducible factors of
![]() $h$
in
$h$
in
![]() $R$
, and
$R$
, and
In particular, this means
![]() $\textrm{deg}(\hat{h})=\frac{dm}{s}$
,
$\textrm{deg}(\hat{h})=\frac{dm}{s}$
,
![]() $\textrm{deg}(h)=km=\frac{dn m}{s}$
, and
$\textrm{deg}(h)=km=\frac{dn m}{s}$
, and
Moreover,
![]() $s$
divides
$s$
divides
![]() $gcd(dm,dn)$
. If
$gcd(dm,dn)$
. If
![]() $f$
is not right-invariant, then
$f$
is not right-invariant, then
![]() $k\gt 1$
and
$k\gt 1$
and
![]() $s\not =dn$
.
$s\not =dn$
.
We know that
![]() $[S_f\;:\;F]=[S_f\;:\;C][C\;:\;F]=d^2m\cdot n$
. Since
$[S_f\;:\;F]=[S_f\;:\;C][C\;:\;F]=d^2m\cdot n$
. Since
![]() $\textrm{Nuc}_r(S_f)$
is a subalgebra of
$\textrm{Nuc}_r(S_f)$
is a subalgebra of
![]() $S_f$
, comparing dimensions we obtain that
$S_f$
, comparing dimensions we obtain that
that is
![]() $[S_f\;:\;\textrm{Nuc}_r(S_f)]=k.$
$[S_f\;:\;\textrm{Nuc}_r(S_f)]=k.$
If
![]() $f$
is not right-invariant which is equivalent to
$f$
is not right-invariant which is equivalent to
![]() $S_f$
being not associative, which in turn is equivalent to
$S_f$
being not associative, which in turn is equivalent to
![]() $k\gt 1$
, then
$k\gt 1$
, then
![]() $s\not =dn$
looking at the degree of
$s\not =dn$
looking at the degree of
![]() $h$
. Note that
$h$
. Note that
![]() $\textrm{deg}(h)=dn m$
is the largest possible degree of
$\textrm{deg}(h)=dn m$
is the largest possible degree of
![]() $h$
.
$h$
.
All of the above applies in particular to the special case that
![]() $D$
is a finite field extension
$D$
is a finite field extension
![]() $K$
of
$K$
of
![]() $C$
of degree
$C$
of degree
![]() $n$
, and
$n$
, and
![]() $\sigma \in \textrm{Aut}(K)$
has order
$\sigma \in \textrm{Aut}(K)$
has order
![]() $n$
. Then,
$n$
. Then,
![]() $R=K[t;\;\sigma ]$
has center
$R=K[t;\;\sigma ]$
has center
![]() $C(R) = F[t^n]=\{\sum _{i=0}^{k}a_i(t^n)^i\,|\, a_i\in F \}= F[x]$
where
$C(R) = F[t^n]=\{\sum _{i=0}^{k}a_i(t^n)^i\,|\, a_i\in F \}= F[x]$
where
![]() $F= \textrm{Fix}(\sigma )$
[Reference Jacobson18, Theorem 1.1.22].
$F= \textrm{Fix}(\sigma )$
[Reference Jacobson18, Theorem 1.1.22].
3. Constructing sets of matrices employing irreducible f
 $\in$
D[t;
$\in$
D[t;
 $\sigma$
]
$\sigma$
]
Let
![]() $R=D[t;\;\sigma ]$
be as in Section 2.3 and
$R=D[t;\;\sigma ]$
be as in Section 2.3 and
![]() $f\in R$
be an irreducible monic polynomial of degree
$f\in R$
be an irreducible monic polynomial of degree
![]() $m\gt 1$
with nonzero constant term and minimal central left multiple
$m\gt 1$
with nonzero constant term and minimal central left multiple
![]() $h(t)=\hat{h}(u^{-1}t^n)$
. Let
$h(t)=\hat{h}(u^{-1}t^n)$
. Let
Together with the multiplication
![]() $(x+Rf)\circ (y+Rf)= (xy)+Rf$
for all
$(x+Rf)\circ (y+Rf)= (xy)+Rf$
for all
![]() $x,y\in F[u^{-1}t^n]$
,
$x,y\in F[u^{-1}t^n]$
,
![]() $E_f$
becomes an
$E_f$
becomes an
![]() $F$
-algebra.
$F$
-algebra.
Lemma 4.
(i) For each
![]() $z(t)=\hat{z}(u^{-1}t^n)\in F[u^{-1}t^n]$
with
$z(t)=\hat{z}(u^{-1}t^n)\in F[u^{-1}t^n]$
with
![]() $\hat{z}\in F[x]$
, we have
$\hat{z}\in F[x]$
, we have
![]() $z\in Rf$
if and only if
$z\in Rf$
if and only if
![]() $z\in Rh$
. (ii)
$z\in Rh$
. (ii)
![]() $(E_f,\circ )$
is a field isomorphic to
$(E_f,\circ )$
is a field isomorphic to
![]() $E_{\hat{h}}$
.
$E_{\hat{h}}$
.
Proof. (i) As
![]() $h=gf$
for some
$h=gf$
for some
![]() $g\in R$
, each
$g\in R$
, each
![]() $z\in Rh$
also lies in
$z\in Rh$
also lies in
![]() $Rf$
.
$Rf$
.
Conversely, let
![]() $z(t)=\hat{z}(u^{-1}t^n)\in F[u^{-1}t^n]$
with
$z(t)=\hat{z}(u^{-1}t^n)\in F[u^{-1}t^n]$
with
![]() $\hat{z}\in F[x]$
be such that
$\hat{z}\in F[x]$
be such that
![]() $z\in Rf$
. By the Euclidean division algorithm in
$z\in Rf$
. By the Euclidean division algorithm in
![]() $F[x]$
, there exist unique
$F[x]$
, there exist unique
![]() $\hat{q}(x),\hat{r}(x)\in F[x]$
such that
$\hat{q}(x),\hat{r}(x)\in F[x]$
such that
![]() $\hat{z}=\hat{q}\hat{h}+\hat{r},$
where
$\hat{z}=\hat{q}\hat{h}+\hat{r},$
where
![]() $\textrm{deg}(\hat{r})\lt \textrm{deg}(\hat{h})=s$
or
$\textrm{deg}(\hat{r})\lt \textrm{deg}(\hat{h})=s$
or
![]() $\hat{r}=0$
. If
$\hat{r}=0$
. If
![]() $\hat{r}\neq 0$
, then
$\hat{r}\neq 0$
, then
![]() $\hat{r}=\hat{z}-\hat{q}\hat{h}$
, i.e. we found
$\hat{r}=\hat{z}-\hat{q}\hat{h}$
, i.e. we found
![]() $q(t)=\hat{q}(u^{-1}t^n),r(t)=\hat{r}(u^{-1}t^n)\in F[u^{-1}t^n]$
, such that
$q(t)=\hat{q}(u^{-1}t^n),r(t)=\hat{r}(u^{-1}t^n)\in F[u^{-1}t^n]$
, such that
![]() $r(t)=z(t)-q(t)h(t)\in Rf.$
Let
$r(t)=z(t)-q(t)h(t)\in Rf.$
Let
![]() $\hat{r'}(x)=r_0^{-1}\hat{r}(x)\in F[x]$
, where
$\hat{r'}(x)=r_0^{-1}\hat{r}(x)\in F[x]$
, where
![]() $r_0\in F^{\times }$
is the leading coefficient of
$r_0\in F^{\times }$
is the leading coefficient of
![]() $\hat{r}(x)$
, then
$\hat{r}(x)$
, then
![]() $r'(t)=\hat{r'}(u^{-1}t^n)$
is monic by definition.
$r'(t)=\hat{r'}(u^{-1}t^n)$
is monic by definition.
As
![]() $r'(t)=\hat{r'}(u^{-1}t^n)\in Rf$
, too, there exists
$r'(t)=\hat{r'}(u^{-1}t^n)\in Rf$
, too, there exists
![]() $a(t)\in R$
such that
$a(t)\in R$
such that
![]() $r'(t)=a(t)f(t)$
. Thus,
$r'(t)=a(t)f(t)$
. Thus,
![]() $r'(t)\in F[u^{-1}t^n]$
is a monic polynomial of degree less than
$r'(t)\in F[u^{-1}t^n]$
is a monic polynomial of degree less than
![]() $s$
which is right divisible by
$s$
which is right divisible by
![]() $f$
. This contradicts the definition of
$f$
. This contradicts the definition of
![]() $h$
as the minimal central left multiple of
$h$
as the minimal central left multiple of
![]() $f$
. Thus, we conclude that
$f$
. Thus, we conclude that
![]() $r=0$
and
$r=0$
and
![]() $z=qh \in Rh$
, as required. (ii)
$z=qh \in Rh$
, as required. (ii)
![]() $E_f$
is a commutative associative ring with identity
$E_f$
is a commutative associative ring with identity
![]() $1+Rf$
. Define the map
$1+Rf$
. Define the map
![]() $G\;:\; E_f\to E_{\hat{h}}$
,
$G\;:\; E_f\to E_{\hat{h}}$
,
![]() $G(z+Rf)=z+Rh$
for all
$G(z+Rf)=z+Rh$
for all
![]() $z\in F[u^{-1}t^n]$
.
$z\in F[u^{-1}t^n]$
.
![]() $G$
is well-defined and surjective. For all
$G$
is well-defined and surjective. For all
![]() $x,y\in F[u^{-1}t^n]$
, we have
$x,y\in F[u^{-1}t^n]$
, we have
![]() $G(x+Rf)+G(y+Rf)=(x+Rh)+(y+Rh)=(x+y)+Rh=G(x+y+Rf),$
$G(x+Rf)+G(y+Rf)=(x+Rh)+(y+Rh)=(x+y)+Rh=G(x+y+Rf),$
![]() $G(1+Rf)=1+Rh$
, and
$G(1+Rf)=1+Rh$
, and
![]() $G(x+Rf)G(y+Rf)=(x+Rh)(y+Rh)=xy+Rh=G(xy+Rf),$
yielding that
$G(x+Rf)G(y+Rf)=(x+Rh)(y+Rh)=xy+Rh=G(xy+Rf),$
yielding that
![]() $G$
is an isomorphism. To check injectivity, we note that
$G$
is an isomorphism. To check injectivity, we note that
![]() $G(x+Rf)=0+Rh$
if and only if
$G(x+Rf)=0+Rh$
if and only if
![]() $x\in Rh$
. By Lemma 4 (i), this implies
$x\in Rh$
. By Lemma 4 (i), this implies
![]() $x\in Rf$
and so
$x\in Rf$
and so
![]() $x+Rf=0+Rf$
.
$x+Rf=0+Rf$
.
Let
![]() $B=\textrm{Nuc}_r(S_f)$
and
$B=\textrm{Nuc}_r(S_f)$
and
![]() $k$
be the number of irreducible factors of
$k$
be the number of irreducible factors of
![]() $h(t)$
in
$h(t)$
in
![]() $R$
.
$R$
.
Lemma 5.
The left
![]() $R$
-module
$R$
-module
![]() $R/Rf$
is a right
$R/Rf$
is a right
![]() $B$
-module of rank
$B$
-module of rank
![]() $k$
via the scalar multiplication
$k$
via the scalar multiplication
![]() $R/Rf\times B\longrightarrow R/Rf$
,
$R/Rf\times B\longrightarrow R/Rf$
,
![]() $(a+Rf)(z+Rf)=az+Rf$
for all
$(a+Rf)(z+Rf)=az+Rf$
for all
![]() $z\in F[u^{-1}t^n]$
and
$z\in F[u^{-1}t^n]$
and
![]() $a\in R$
. We can identify
$a\in R$
. We can identify
![]() $R/Rf$
with
$R/Rf$
with
![]() $B^{k}$
via a canonical basis.
$B^{k}$
via a canonical basis.
Proof. Since the Petit algebra
![]() $S_f=R/Rf$
with its multiplication
$S_f=R/Rf$
with its multiplication
![]() $ab=ab \, \textrm{mod}_r\, f$
is a nonassociative unital algebra with right nucleus
$ab=ab \, \textrm{mod}_r\, f$
is a nonassociative unital algebra with right nucleus
![]() $B$
,
$B$
,
![]() $R/Rf$
is a right
$R/Rf$
is a right
![]() $B$
-module via the given scalar multiplication. As
$B$
-module via the given scalar multiplication. As
![]() $R/Rf$
is a vector space of dimension
$R/Rf$
is a vector space of dimension
![]() $d^2mn$
over
$d^2mn$
over
![]() $F$
,
$F$
,
![]() $R/Rf$
is free of rank
$R/Rf$
is free of rank
![]() $k$
over
$k$
over
![]() $B$
.
$B$
.
Let
![]() $\nu \in D^\times$
and
$\nu \in D^\times$
and
![]() $\rho \in \textrm{Aut}(D)$
, and define
$\rho \in \textrm{Aut}(D)$
, and define
![]() $F'=\textrm{Fix}(\rho )\cap F$
. We assume in the following that
$F'=\textrm{Fix}(\rho )\cap F$
. We assume in the following that
![]() $F/F'$
is finite-dimensional. Let
$F/F'$
is finite-dimensional. Let
![]() $s$
be the degree of
$s$
be the degree of
![]() $B$
over
$B$
over
![]() $E_{\hat{h}}$
. We assume
$E_{\hat{h}}$
. We assume
![]() $f$
is not right-invariant, i.e.
$f$
is not right-invariant, i.e.
![]() $k\gt 1$
.
$k\gt 1$
.
Let
![]() $l\lt k=dn/s$
be a positive integer. Define the set
$l\lt k=dn/s$
be a positive integer. Define the set
![]() $S_{n,m,l}(\nu,\rho, f)=\lbrace a+Rh\,|\, a\in P\rbrace \subset R/Rh,$
where
$S_{n,m,l}(\nu,\rho, f)=\lbrace a+Rh\,|\, a\in P\rbrace \subset R/Rh,$
where
![]() $S_{n,m,l}(\nu,\rho, f)$
is a vector space over
$S_{n,m,l}(\nu,\rho, f)$
is a vector space over
![]() $F'$
of dimension
$F'$
of dimension
![]() $d^2nml[F\;:\;F']$
.
$d^2nml[F\;:\;F']$
.
![]() $R/Rf$
is a right
$R/Rf$
is a right
![]() $B$
-module of rank
$B$
-module of rank
![]() $k$
, as shown above. Let
$k$
, as shown above. Let
![]() $L_a\;:\;R/Rf\to R/Rf$
be the left multiplication map
$L_a\;:\;R/Rf\to R/Rf$
be the left multiplication map
![]() $L_a(b+Rf)=ab+Rf$
. Then,
$L_a(b+Rf)=ab+Rf$
. Then,
![]() $L_a$
is
$L_a$
is
![]() $B$
-linear, as we have
$B$
-linear, as we have
![]() $a( x \alpha )= ( ax) \alpha$
for all
$a( x \alpha )= ( ax) \alpha$
for all
![]() $\alpha \in B$
,
$\alpha \in B$
,
![]() $a,x\in R/Rf$
, and therefore,
$a,x\in R/Rf$
, and therefore,
![]() $L_a( x \alpha )= L_a(x) \alpha$
for all
$L_a( x \alpha )= L_a(x) \alpha$
for all
![]() $\alpha \in B$
. Thus,
$\alpha \in B$
. Thus,
![]() $L_a\in \textrm{End}_{B}(R/Rf)$
and
$L_a\in \textrm{End}_{B}(R/Rf)$
and
by Theorem 3. Hence, we have well-defined maps
where
![]() $M_a$
is the matrix representing
$M_a$
is the matrix representing
![]() $L_a$
with respect to a
$L_a$
with respect to a
![]() $B$
-basis of
$B$
-basis of
![]() $R/Rf$
. We denote the image of
$R/Rf$
. We denote the image of
![]() $S_{n,m,l}(\nu,\rho,h)$
in
$S_{n,m,l}(\nu,\rho,h)$
in
![]() $M_{k}(B)$
by
$M_{k}(B)$
by
The code
![]() $\mathcal{C}=\mathcal{C}_{n,m,l}$
is
$\mathcal{C}=\mathcal{C}_{n,m,l}$
is
![]() $F'$
-linear by construction, and a generalized rank metric code. If
$F'$
-linear by construction, and a generalized rank metric code. If
![]() $\mathcal{C}$
has minimum distance
$\mathcal{C}$
has minimum distance
![]() $d_{\mathcal{C}}$
, the Singleton-like bound canonically generalizes to the bound
$d_{\mathcal{C}}$
, the Singleton-like bound canonically generalizes to the bound
with
![]() $[B\;:\;F']=s[F\;:\;F']$
. If
$[B\;:\;F']=s[F\;:\;F']$
. If
![]() $d_{\mathcal{C}}=k-l+1$
, then
$d_{\mathcal{C}}=k-l+1$
, then
![]() $\textrm{dim}_{F'}(S_{n,m,l}(\nu,\rho, f))=d^2nml/dms [B\;:\;F']=d^2mnl$
$\textrm{dim}_{F'}(S_{n,m,l}(\nu,\rho, f))=d^2nml/dms [B\;:\;F']=d^2mnl$
![]() $[F\;:\;F'] = lk [B\;:\;F']=lkdms[F\;:\;F']$
. Thus, if
$[F\;:\;F'] = lk [B\;:\;F']=lkdms[F\;:\;F']$
. Thus, if
![]() $d_{\mathcal{C}}=k-l+1$
, then
$d_{\mathcal{C}}=k-l+1$
, then
![]() $\mathcal{C}$
attains this bound and
$\mathcal{C}$
attains this bound and
![]() $\mathcal{C}$
is a maximum rank distance code in
$\mathcal{C}$
is a maximum rank distance code in
![]() $M_k(B)$
.
$M_k(B)$
.
We will usually deal with the case that
![]() $\textrm{deg }(h)=dmn$
, so that
$\textrm{deg }(h)=dmn$
, so that
![]() $B=E_{\hat{h}}$
is a field,
$B=E_{\hat{h}}$
is a field,
![]() $s=1,$
and
$s=1,$
and
![]() $\mathcal{C}_{n,m,l}\subset M_{dn}(E_f)$
. Note that if
$\mathcal{C}_{n,m,l}\subset M_{dn}(E_f)$
. Note that if
![]() $l=1$
and
$l=1$
and
![]() $d_{\mathcal{{C}}}=k$
, this generalized Singleton-like bound is achieved trivially: we obtain examples of MRD codes in
$d_{\mathcal{{C}}}=k$
, this generalized Singleton-like bound is achieved trivially: we obtain examples of MRD codes in
![]() $M_k(B)$
. This arises when we look at division algebras
$M_k(B)$
. This arises when we look at division algebras
![]() $S_{n,m,1}(\nu,\rho, f)$
and the matrices representing their left multiplication, cf. Remark 17 and Corollary 18.
$S_{n,m,1}(\nu,\rho, f)$
and the matrices representing their left multiplication, cf. Remark 17 and Corollary 18.
4. The rank of the matrix that corresponds to the element
 $\boldsymbol{{a}}\boldsymbol{+}\boldsymbol{{Rh}}$
$\boldsymbol{{a}}\boldsymbol{+}\boldsymbol{{Rh}}$
Let
![]() $ R=D[t;\;\sigma ]$
be as in Section 3, and
$ R=D[t;\;\sigma ]$
be as in Section 3, and
![]() $f\in R$
be an irreducible monic polynomial of degree
$f\in R$
be an irreducible monic polynomial of degree
![]() $m\gt 1$
with minimal central left multiple
$m\gt 1$
with minimal central left multiple
![]() $h$
. Let
$h$
. Let
![]() $B=\textrm{Nuc}_r(S_f)$
. We have
$B=\textrm{Nuc}_r(S_f)$
. We have
![]() $\textrm{deg}(\hat{h})=km$
and
$\textrm{deg}(\hat{h})=km$
and
![]() $R/Rh\cong M_{k}(B)$
as
$R/Rh\cong M_{k}(B)$
as
![]() $E_{\hat{h}}$
-algebras by Theorem 3. Let
$E_{\hat{h}}$
-algebras by Theorem 3. Let
![]() $\Psi \;:\;R/Rh\to M_k(B),$
$\Psi \;:\;R/Rh\to M_k(B),$
![]() $\Psi (a+Rh)=M_a$
, be this isomorphism. For
$\Psi (a+Rh)=M_a$
, be this isomorphism. For
![]() $M_a\in M_k(B)$
, consider the right
$M_a\in M_k(B)$
, consider the right
![]() $B$
-linear map
$B$
-linear map
![]() $L_{M_a}\;:\;M_k(B)\to M_k(B)$
,
$L_{M_a}\;:\;M_k(B)\to M_k(B)$
,
![]() $L_{M_a}\;:\;X\mapsto M_aX.$
Then, we obtain the following generalization of [Reference Sheekey34], Proposition 7 (which was only proved for
$L_{M_a}\;:\;X\mapsto M_aX.$
Then, we obtain the following generalization of [Reference Sheekey34], Proposition 7 (which was only proved for
![]() $f$
with coefficients in a finite field, i.e. for the special case that
$f$
with coefficients in a finite field, i.e. for the special case that
![]() $\textrm{deg}(h)=nm$
is maximal):
$\textrm{deg}(h)=nm$
is maximal):
Theorem 6.
Let
![]() $\textrm{deg}(h)=km$
. Then
$\textrm{deg}(h)=km$
. Then
![]() $M_a\in M_{k}(B)$
and
$M_a\in M_{k}(B)$
and
for all
![]() $a+Rh\in R/Rh$
. In particular, if
$a+Rh\in R/Rh$
. In particular, if
![]() $\textrm{deg}(h)=dmn$
, then
$\textrm{deg}(h)=dmn$
, then
![]() $M_a\in M_n(E_{\hat{h}})$
, and
$M_a\in M_n(E_{\hat{h}})$
, and
Proof. For each
![]() $M_a\in M_k(B)$
, define
$M_a\in M_k(B)$
, define
![]() $\textrm{Ann}_r(M_a)=\lbrace N\in M_k(B)\,|\, M_aN=0\rbrace$
. Then,
$\textrm{Ann}_r(M_a)=\lbrace N\in M_k(B)\,|\, M_aN=0\rbrace$
. Then,
![]() $\textrm{Ann}_r(M_a)$
is the kernel of the endomorphism
$\textrm{Ann}_r(M_a)$
is the kernel of the endomorphism
![]() $L_{M_a}\;:\;M_k(B)\to M_k(B)$
. By the Rank-Nullity Theorem for free right
$L_{M_a}\;:\;M_k(B)\to M_k(B)$
. By the Rank-Nullity Theorem for free right
![]() $B$
-modules of finite rank [Reference Hungerford16, ch. IV, Cor. 2.14], it follows that
$B$
-modules of finite rank [Reference Hungerford16, ch. IV, Cor. 2.14], it follows that
We conclude that
![]() $\textrm{dim}_{B}(im(L_{M_a}))= k^2-\textrm{dim}_{B}(\textrm{Ann}_r(M_a)).$
Now for each
$\textrm{dim}_{B}(im(L_{M_a}))= k^2-\textrm{dim}_{B}(\textrm{Ann}_r(M_a)).$
Now for each
![]() $b+Rh$
,
$b+Rh$
,
![]() $M_aM_b=0$
if and only if
$M_aM_b=0$
if and only if
![]() $\Psi (a+Rh)\Psi (b+Rh)=0$
. As
$\Psi (a+Rh)\Psi (b+Rh)=0$
. As
![]() $\Psi$
is multiplicative, this is true if and only if
$\Psi$
is multiplicative, this is true if and only if
![]() $\Psi ((a+Rh)(b+Rh))=0$
. This means
$\Psi ((a+Rh)(b+Rh))=0$
. This means
![]() $(a+Rh)(b+Rh)=0$
. Hence, it is clear that
$(a+Rh)(b+Rh)=0$
. Hence, it is clear that
![]() $\textrm{Ann}_r(M_a)\cong \textrm{Ann}_r(a)$
, where
$\textrm{Ann}_r(M_a)\cong \textrm{Ann}_r(a)$
, where
so
![]() $\textrm{dim}(\textrm{Ann}_r(M_a))=\textrm{dim}(\textrm{Ann}_r(a))$
. Let
$\textrm{dim}(\textrm{Ann}_r(M_a))=\textrm{dim}(\textrm{Ann}_r(a))$
. Let
![]() $\gamma =gcrd(a,h)$
so
$\gamma =gcrd(a,h)$
so
![]() $h=\delta \gamma$
for some
$h=\delta \gamma$
for some
![]() $\delta \in R$
. As
$\delta \in R$
. As
![]() $h\in C(R)$
and
$h\in C(R)$
and
![]() $R$
is a domain, we also have
$R$
is a domain, we also have
![]() $h=\gamma \delta$
by Lemma 1. Let
$h=\gamma \delta$
by Lemma 1. Let
![]() $b\in R$
be the unique element such that
$b\in R$
be the unique element such that
![]() $a=b\gamma$
. Then,
$a=b\gamma$
. Then,
![]() $gcrd(b,\delta )=1$
, else
$gcrd(b,\delta )=1$
, else
![]() $\gamma$
is not the greatest common right divisor of
$\gamma$
is not the greatest common right divisor of
![]() $a$
and
$a$
and
![]() $h$
.Let
$h$
.Let
![]() $v\in R$
. By the left Euclidean division algorithm, there exist unique
$v\in R$
. By the left Euclidean division algorithm, there exist unique
![]() $u,w\in R$
such that
$u,w\in R$
such that
![]() $v=\delta u+w$
where
$v=\delta u+w$
where
![]() $deg(w)\lt \textrm{deg}(\delta )$
and
$deg(w)\lt \textrm{deg}(\delta )$
and
![]() $\textrm{gcld}(w,\delta )=1$
. It follows that
$\textrm{gcld}(w,\delta )=1$
. It follows that
![]() $av = a\delta u+aw = b\gamma \delta u+ b\gamma w = bhu+b\gamma w,$
and therefore,
$av = a\delta u+aw = b\gamma \delta u+ b\gamma w = bhu+b\gamma w,$
and therefore,
![]() $av+Rh=b\gamma w+Rh$
. Suppose
$av+Rh=b\gamma w+Rh$
. Suppose
![]() $b\gamma w\equiv 0 \textrm{mod}_rh$
. As
$b\gamma w\equiv 0 \textrm{mod}_rh$
. As
![]() $gcrd(b,\delta )=1$
, there exist
$gcrd(b,\delta )=1$
, there exist
![]() $c,d\in R$
such that
$c,d\in R$
such that
![]() $cb+d\delta =1$
, so
$cb+d\delta =1$
, so
![]() $cb\gamma +d\delta \gamma =\gamma .$
As
$cb\gamma +d\delta \gamma =\gamma .$
As
![]() $\delta \gamma =h$
, this implies
$\delta \gamma =h$
, this implies
![]() $cb\gamma \equiv \gamma \;:\; \textrm{mod}_rh$
. Hence,
$cb\gamma \equiv \gamma \;:\; \textrm{mod}_rh$
. Hence,
![]() $\gamma w\equiv cb\gamma w\equiv 0\;:\; \textrm{mod}_rh.$
However,
$\gamma w\equiv cb\gamma w\equiv 0\;:\; \textrm{mod}_rh.$
However,
![]() $\textrm{deg}(w)\lt deg(\delta )$
so
$\textrm{deg}(w)\lt deg(\delta )$
so
![]() $\textrm{deg}(\gamma w)\lt \textrm{deg}(\gamma \delta )=\textrm{deg}(h)$
; due to this,
$\textrm{deg}(\gamma w)\lt \textrm{deg}(\gamma \delta )=\textrm{deg}(h)$
; due to this,
![]() $\gamma w\equiv 0\;:\; \textrm{mod}_rh$
implies that
$\gamma w\equiv 0\;:\; \textrm{mod}_rh$
implies that
![]() $\gamma w=0$
. As
$\gamma w=0$
. As
![]() $\gamma \neq 0$
and
$\gamma \neq 0$
and
![]() $R$
is a domain, we conclude that
$R$
is a domain, we conclude that
![]() $w=0$
.Hence,
$w=0$
.Hence,
![]() $(a+Rh)(v+Rh)=0+Rh$
if and only if
$(a+Rh)(v+Rh)=0+Rh$
if and only if
![]() $v=\delta u$
where
$v=\delta u$
where
![]() $\textrm{deg}(u)\lt \textrm{deg}(\gamma )$
. As
$\textrm{deg}(u)\lt \textrm{deg}(\gamma )$
. As
![]() $\delta$
is uniquely defined by
$\delta$
is uniquely defined by
![]() $a$
and
$a$
and
![]() $h$
, every element of
$h$
, every element of
![]() $\textrm{Ann}_r(a)$
is determined by
$\textrm{Ann}_r(a)$
is determined by
![]() $u\in R$
such that
$u\in R$
such that
![]() $\textrm{deg}(u)\lt \textrm{deg}(\gamma )$
. Thus,
$\textrm{deg}(u)\lt \textrm{deg}(\gamma )$
. Thus,
As
![]() $\lbrace 1, t,\dots, t^{ deg(\gamma )-1}\rbrace$
is a
$\lbrace 1, t,\dots, t^{ deg(\gamma )-1}\rbrace$
is a
![]() $D$
-basis for the free left
$D$
-basis for the free left
![]() $D$
-module
$D$
-module
![]() $R_{\gamma }$
, it follows that
$R_{\gamma }$
, it follows that
![]() $\textrm{dim}_{D}(\textrm{Ann}_r(a))=\textrm{deg}(\gamma )$
, so
$\textrm{dim}_{D}(\textrm{Ann}_r(a))=\textrm{deg}(\gamma )$
, so
![]() $\textrm{dim}_{F}(\textrm{Ann}_r(a))=\textrm{deg}(\gamma )d^2n$
. Since
$\textrm{dim}_{F}(\textrm{Ann}_r(a))=\textrm{deg}(\gamma )d^2n$
. Since
![]() $\textrm{dim}_{E_{\hat{h}}}(B)=s^2=d^2n^2/k^2$
and
$\textrm{dim}_{E_{\hat{h}}}(B)=s^2=d^2n^2/k^2$
and
![]() $[E_{\hat{h}}\;:\;F]=km/n$
, we obtain
$[E_{\hat{h}}\;:\;F]=km/n$
, we obtain
![]() $\textrm{dim}_F(B)=d^2mn/k$
. Hence, we get
$\textrm{dim}_F(B)=d^2mn/k$
. Hence, we get
and so
Let
![]() $\underline{c_i}$
, respectively
$\underline{c_i}$
, respectively
![]() $\underline{r_i}$
, denote the columns, and rows of
$\underline{r_i}$
, denote the columns, and rows of
![]() $M_a$
and
$M_a$
and
![]() $\underline{x_i}$
denote the columns of
$\underline{x_i}$
denote the columns of
![]() $X$
. Computing the matrix using dot product notation, we have
$X$
. Computing the matrix using dot product notation, we have
 \begin{equation*} M_aX=\left ( \begin {array}{c@{\quad}c@{\quad}c} \underline {r_1}\cdot \underline {x_1}&\dots &\underline {r_1}\cdot \underline {x_k}\\ \vdots & \ddots & \vdots \\ \underline {r_k}\cdot \underline {x_1}&\dots & \underline {r_k}\cdot \underline {x_k} \end {array}\right ) \end{equation*}
\begin{equation*} M_aX=\left ( \begin {array}{c@{\quad}c@{\quad}c} \underline {r_1}\cdot \underline {x_1}&\dots &\underline {r_1}\cdot \underline {x_k}\\ \vdots & \ddots & \vdots \\ \underline {r_k}\cdot \underline {x_1}&\dots & \underline {r_k}\cdot \underline {x_k} \end {array}\right ) \end{equation*}
The
![]() $i^{th}$
column of
$i^{th}$
column of
![]() $M_aX$
is equal to
$M_aX$
is equal to
 \begin{equation*} \begin {pmatrix} \underline {r_1}\cdot \underline {x_i}\\ \vdots \\ \underline {r_k}\cdot \underline {x_i} \end {pmatrix} =\underline {c_1}\lambda _1+\dots +\underline {c_k}\lambda _k \end{equation*}
\begin{equation*} \begin {pmatrix} \underline {r_1}\cdot \underline {x_i}\\ \vdots \\ \underline {r_k}\cdot \underline {x_i} \end {pmatrix} =\underline {c_1}\lambda _1+\dots +\underline {c_k}\lambda _k \end{equation*}
for some
![]() $\lambda _j\in B$
. Hence, the dimension of the right
$\lambda _j\in B$
. Hence, the dimension of the right
![]() $B$
-module generated by the
$B$
-module generated by the
![]() $i^{th}$
column of
$i^{th}$
column of
![]() $M_aX$
is exactly the column rank of
$M_aX$
is exactly the column rank of
![]() $M_a$
. As there are
$M_a$
. As there are
![]() $k$
columns of
$k$
columns of
![]() $M_aX$
, it follows that
$M_aX$
, it follows that
![]() $\textrm{dim}_B(\textrm{im}(L_{M_a}))=k \,\textrm{colrank}(M_a)$
.
$\textrm{dim}_B(\textrm{im}(L_{M_a}))=k \,\textrm{colrank}(M_a)$
.
All of the above applies in particular to the special case that
![]() $K/F$
is a field extension and
$K/F$
is a field extension and
![]() $\sigma \in \textrm{Aut}_F(K)$
of finite order
$\sigma \in \textrm{Aut}_F(K)$
of finite order
![]() $n$
,
$n$
,
![]() $R=K[t;\;\sigma ]$
and
$R=K[t;\;\sigma ]$
and
![]() $C(R) = F[t^n]\cong F[x]$
. Let
$C(R) = F[t^n]\cong F[x]$
. Let
![]() $f\in R$
be a monic irreducible polynomial of degree
$f\in R$
be a monic irreducible polynomial of degree
![]() $m\gt 1$
,
$m\gt 1$
,
![]() $B=\textrm{Nuc}_r(S_f)$
, and
$B=\textrm{Nuc}_r(S_f)$
, and
![]() $h(t)=\hat{h}(t^n)$
its minimal central left multiple,
$h(t)=\hat{h}(t^n)$
its minimal central left multiple,
![]() $\textrm{deg}(\hat{h})=km$
. Then,
$\textrm{deg}(\hat{h})=km$
. Then,
![]() $\Psi \;:\;R/Rh\to M_k(B),$
$\Psi \;:\;R/Rh\to M_k(B),$
![]() $\Psi (a+Rh)=M_a$
is an
$\Psi (a+Rh)=M_a$
is an
![]() $E_f$
-algebra isomorphism. For each
$E_f$
-algebra isomorphism. For each
![]() $M_a\in M_k(B)$
, we have the endomorphism
$M_a\in M_k(B)$
, we have the endomorphism
![]() $L_{M_a}\;:\;M_k(B)\to M_k(B)$
by
$L_{M_a}\;:\;M_k(B)\to M_k(B)$
by
![]() $L_{M_a}\;:\;X\mapsto M_aX.$
Analogously to Theorem 6, we can prove:
$L_{M_a}\;:\;X\mapsto M_aX.$
Analogously to Theorem 6, we can prove:
Theorem 7 (for fnite fields and thus deg(h) = nm maximal, cf. [Reference Sheekey34], Proposition 7). Suppose that
![]() $\textrm{deg}(h)=km$
, then for all
$\textrm{deg}(h)=km$
, then for all
![]() $a+Rh\in R/Rh$
we have
$a+Rh\in R/Rh$
we have
In particular, if
![]() $\textrm{deg}(h)=mn$
then
$\textrm{deg}(h)=mn$
then
![]() $M_a\in M_n(E_{\hat{h}})$
and
$M_a\in M_n(E_{\hat{h}})$
and
![]() $\textrm{rank}(M_a)= n - \frac{1}{m}\textrm{deg}(\textrm{gcrd}(a,h))$
.
$\textrm{rank}(M_a)= n - \frac{1}{m}\textrm{deg}(\textrm{gcrd}(a,h))$
.
This generalizes [Reference Sheekey34, Remark 6].
5. Using the norm of
 $\boldsymbol{{D}}(\boldsymbol{{t}};\; \boldsymbol\sigma )$
to investigate
$\boldsymbol{{D}}(\boldsymbol{{t}};\; \boldsymbol\sigma )$
to investigate
 $\boldsymbol{{f}}$
$\boldsymbol{{f}}$
5.1. The algebra (D(x),
 $\widetilde{\sigma }$
, ux)
$\widetilde{\sigma }$
, ux)
Let
![]() $C/F$
be a finite cyclic field extension of degree
$C/F$
be a finite cyclic field extension of degree
![]() $n$
with
$n$
with
![]() $\textrm{Gal}(C/F) = \langle \sigma \rangle$
. Let
$\textrm{Gal}(C/F) = \langle \sigma \rangle$
. Let
![]() $D$
be a finite-dimensional division algebra of degree
$D$
be a finite-dimensional division algebra of degree
![]() $d$
with center
$d$
with center
![]() $C$
and suppose that
$C$
and suppose that
![]() $\sigma$
extends to a
$\sigma$
extends to a
![]() $C$
-algebra automorphism of
$C$
-algebra automorphism of
![]() $D$
that we call
$D$
that we call
![]() $\sigma$
, too. Let
$\sigma$
, too. Let
![]() $R=D[t;\;\sigma ]$
as in Section 3. Then, there exists
$R=D[t;\;\sigma ]$
as in Section 3. Then, there exists
![]() $u \in D^\times$
such that
$u \in D^\times$
such that
![]() $\sigma ^n = i_u$
and
$\sigma ^n = i_u$
and
![]() $\sigma (u) = u$
. These two relations determine
$\sigma (u) = u$
. These two relations determine
![]() $u$
up to multiplication with elements from
$u$
up to multiplication with elements from
![]() $F^\times$
[Reference Pierce25, Lemma 19.7].
$F^\times$
[Reference Pierce25, Lemma 19.7].
The quotient algebra
![]() $(D,\sigma,a)=D[t;\;\sigma ]/(t^n-a)D[t;\;\sigma ]$
, where
$(D,\sigma,a)=D[t;\;\sigma ]/(t^n-a)D[t;\;\sigma ]$
, where
![]() $f(t)=t^n-a\in D[t;\;\sigma ]$
with
$f(t)=t^n-a\in D[t;\;\sigma ]$
with
![]() $d\in F^\times$
, is called a generalized cyclic algebra. The special case where
$d\in F^\times$
, is called a generalized cyclic algebra. The special case where
![]() $D=C$
yields the cyclic algebra
$D=C$
yields the cyclic algebra
![]() $(C/F,\gamma,a)$
[Reference Jacobson18, p. 19].
$(C/F,\gamma,a)$
[Reference Jacobson18, p. 19].
Let
![]() $D(t;\;\sigma ) = \{f/g \,|\, f \in D[t;\;\sigma ], g \in C(D[t;\;\sigma ])\}$
be the ring of central quotients of
$D(t;\;\sigma ) = \{f/g \,|\, f \in D[t;\;\sigma ], g \in C(D[t;\;\sigma ])\}$
be the ring of central quotients of
![]() $D[t;\;\sigma ]$
. Let
$D[t;\;\sigma ]$
. Let
![]() $\widetilde{\sigma }$
denote the extension of
$\widetilde{\sigma }$
denote the extension of
![]() $\sigma$
to
$\sigma$
to
![]() $D(x)$
that fixes
$D(x)$
that fixes
![]() $x$
[Reference Hanke14, Lemma 2.1]. Then,
$x$
[Reference Hanke14, Lemma 2.1]. Then,
![]() $C(D(t;\; \sigma )) = \textrm{Quot}(C(D[t;\;\sigma ])) = F(x)$
,
$C(D(t;\; \sigma )) = \textrm{Quot}(C(D[t;\;\sigma ])) = F(x)$
,
![]() $x =u^{-1}t^n$
, is the center of
$x =u^{-1}t^n$
, is the center of
![]() $D(t;\;\sigma )$
, where
$D(t;\;\sigma )$
, where
![]() $\textrm{Quot}(U)$
denotes the quotient field of an integral domain
$\textrm{Quot}(U)$
denotes the quotient field of an integral domain
![]() $U$
. More precisely,
$U$
. More precisely,
![]() $D(t;\;\sigma ) \cong (D(x), \widetilde{\sigma }, ux )$
is a generalized cyclic algebra of degree
$D(t;\;\sigma ) \cong (D(x), \widetilde{\sigma }, ux )$
is a generalized cyclic algebra of degree
![]() $dn$
over its center
$dn$
over its center
![]() $F(x)$
and a division algebra [Reference Hanke14, Theorems 2.2, 2.3].
$F(x)$
and a division algebra [Reference Hanke14, Theorems 2.2, 2.3].
Let
![]() $N$
be the reduced norm of
$N$
be the reduced norm of
![]() $(D(x), \widetilde{\sigma }, ux )$
.
$(D(x), \widetilde{\sigma }, ux )$
.
Lemma 8.
Let
![]() $f\in R$
. If
$f\in R$
. If
![]() $N(f)$
is irreducible in
$N(f)$
is irreducible in
![]() $F[x],$
then
$F[x],$
then
![]() $f$
is irreducible in
$f$
is irreducible in
![]() $R$
.
$R$
.
Proof. If
![]() $f=gp$
for
$f=gp$
for
![]() $g,p\in R$
then
$g,p\in R$
then
![]() $N(f)=N(g)N(p)$
is reducible in
$N(f)=N(g)N(p)$
is reducible in
![]() $F[x],$
since both
$F[x],$
since both
![]() $N(g)$
and
$N(g)$
and
![]() $N(p)$
lie in
$N(p)$
lie in
![]() $F[x]$
, which immediately yields the assertion.
$F[x]$
, which immediately yields the assertion.
From now on, we assume that
Then,
![]() $\sigma |_E$
has order
$\sigma |_E$
has order
![]() $n$
. Write
$n$
. Write
![]() $m=kn+r$
for some
$m=kn+r$
for some
![]() $0\leq r\lt n$
. Let
$0\leq r\lt n$
. Let
![]() $f=\sum _{i=0}^ma_it^i\in R$
be a polynomial such that
$f=\sum _{i=0}^ma_it^i\in R$
be a polynomial such that
![]() $a_0\not =0$
and
$a_0\not =0$
and
![]() $h\in R$
be the minimal central left multiple of
$h\in R$
be the minimal central left multiple of
![]() $f$
in
$f$
in
![]() $R$
.
$R$
.
Theorem 9 [Reference Thompson and Pumplün36]. For
![]() $f\in E[t;\;\sigma ]\subset D[t;\;\sigma ]$
, we have
$f\in E[t;\;\sigma ]\subset D[t;\;\sigma ]$
, we have
Theorem 10.
Suppose that
![]() $\textrm{deg}(h)=dmn$
.
$\textrm{deg}(h)=dmn$
.
-
(i) [Reference Thompson and Pumplün36, Theorem 14 (i)] If
 $\hat{h}$
is irreducible in
$\hat{h}$
is irreducible in
 $F[x]$
, then
$F[x]$
, then
 $f$
is irreducible in
$f$
is irreducible in
 $R$
.
$R$
. -
(ii) [Reference Thompson and Pumplün36, Theorem 14 (ii)] If
 $f$
is irreducible, then
$f$
is irreducible, then
 $N(f)$
is irreducible in
$N(f)$
is irreducible in
 $F[x]$
.
$F[x]$
. -
(iii) If
 $f\in E[t;\;\sigma ]$
, then
$f\in E[t;\;\sigma ]$
, then
 $N(f)= (\!-\!1)^{dr(n-1)}N_{E/F}(a_m)N_{E/C}(u)^{m} \hat{h}$
and
$N(f)= (\!-\!1)^{dr(n-1)}N_{E/F}(a_m)N_{E/C}(u)^{m} \hat{h}$
and
if
![]() $h_0$
denotes the constant term of
$h_0$
denotes the constant term of
![]() $\hat{h}$
.
$\hat{h}$
.
Proof. (iii) By Theorem 9, we have
![]() $\textrm{deg}(N(f))=dmn$
in
$\textrm{deg}(N(f))=dmn$
in
![]() $R$
.
$R$
.
![]() $N(f)$
is a two-sided multiple of
$N(f)$
is a two-sided multiple of
![]() $f$
in
$f$
in
![]() $R$
; therefore, the bound
$R$
; therefore, the bound
![]() $f^*$
of
$f^*$
of
![]() $f$
divides
$f$
divides
![]() $N(f)$
in
$N(f)$
in
![]() $R$
. Since
$R$
. Since
![]() $(f,t)_r=1,$
$(f,t)_r=1,$
![]() $f^*\in C(R)$
and therefore
$f^*\in C(R)$
and therefore
![]() $f^*$
equals
$f^*$
equals
![]() $h$
up to some factor in
$h$
up to some factor in
![]() $F^\times$
. Thus,
$F^\times$
. Thus,
![]() $h(t)=\hat{h}(u^{-1}t^n)$
must divide
$h(t)=\hat{h}(u^{-1}t^n)$
must divide
![]() $N(f)$
in
$N(f)$
in
![]() $R$
. Write
$R$
. Write
![]() $N(f)=g (t)h(t)$
for some
$N(f)=g (t)h(t)$
for some
![]() $g\in R$
. Comparing degrees in
$g\in R$
. Comparing degrees in
![]() $R$
, we obtain
$R$
, we obtain
![]() $\textrm{deg} N(f)=\textrm{deg}(g(t))+dmn=dmn$
, which implies
$\textrm{deg} N(f)=\textrm{deg}(g(t))+dmn=dmn$
, which implies
![]() $\textrm{deg}(g)=0$
, i.e.
$\textrm{deg}(g)=0$
, i.e.
![]() $g(t)=a\in A^\times$
. This implies that
$g(t)=a\in A^\times$
. This implies that
![]() $N(f)=ah(t)=a \hat{h}(u^{-1}t^n)$
. Comparing highest coefficients of
$N(f)=ah(t)=a \hat{h}(u^{-1}t^n)$
. Comparing highest coefficients of
![]() $N(f)$
and
$N(f)$
and
![]() $a\hat{h}$
yields that
$a\hat{h}$
yields that
![]() $a=(\!-\!1)^{dr(n-1)}N_{E/F}(a_m)N_{E/C}(u)^{m}$
by Theorem 9, so that comparing constant terms we get that
$a=(\!-\!1)^{dr(n-1)}N_{E/F}(a_m)N_{E/C}(u)^{m}$
by Theorem 9, so that comparing constant terms we get that
![]() $N_{E/F}(a_0)=(\!-\!1)^{dr(n-1)}$
$N_{E/F}(a_0)=(\!-\!1)^{dr(n-1)}$
![]() $N_{E/F}(a_m)N_{E/C}(u)^{m}h_0$
, if
$N_{E/F}(a_m)N_{E/C}(u)^{m}h_0$
, if
![]() $h_0$
is the constant term of
$h_0$
is the constant term of
![]() $\hat{h}(x)$
.
$\hat{h}(x)$
.
Theorem 11.
Let
![]() $f\in E[t;\;\sigma ]\subset R$
be monic and irreducible of degree
$f\in E[t;\;\sigma ]\subset R$
be monic and irreducible of degree
![]() $m$
. Let
$m$
. Let
![]() $\textrm{deg}(\hat{h})=dm$
and suppose that all the monic polynomials similar to
$\textrm{deg}(\hat{h})=dm$
and suppose that all the monic polynomials similar to
![]() $f$
lie in
$f$
lie in
![]() $E[t;\;\sigma ]$
. If
$E[t;\;\sigma ]$
. If
![]() $g$
is a monic divisor of
$g$
is a monic divisor of
![]() $h$
in
$h$
in
![]() $R$
of degree
$R$
of degree
![]() $lm$
, then
$lm$
, then
Proof. We know that
![]() $h(t)=\hat{h}(u^{-1}t^n)$
, with
$h(t)=\hat{h}(u^{-1}t^n)$
, with
![]() $\hat{h}(x)$
irreducible in
$\hat{h}(x)$
irreducible in
![]() $F[x]$
, since
$F[x]$
, since
![]() $f$
is irreducible. Thus,
$f$
is irreducible. Thus,
![]() $h$
is a t.s.m. element in Jacobson’s terminology [Reference Jacobson18] and the irreducible factors
$h$
is a t.s.m. element in Jacobson’s terminology [Reference Jacobson18] and the irreducible factors
![]() $f_1(t),\dots, f_k(t)$
of any decomposition of
$f_1(t),\dots, f_k(t)$
of any decomposition of
![]() $h(t)$
are all similar and are all similar to
$h(t)$
are all similar and are all similar to
![]() $f$
, as
$f$
, as
![]() $f$
must be one of them by the definition of
$f$
must be one of them by the definition of
![]() $h$
. Now,
$h$
. Now,
![]() $g(t)$
is a monic divisor of
$g(t)$
is a monic divisor of
![]() $h$
. Thus, we can decompose
$h$
. Thus, we can decompose
![]() $g(t)$
into a product of irreducible factors and up to similarity the irreducible factors of
$g(t)$
into a product of irreducible factors and up to similarity the irreducible factors of
![]() $g$
will be the same as suitably chosen irreducible factors of
$g$
will be the same as suitably chosen irreducible factors of
![]() $h$
by [Reference Jacobson18, Theorem 1.2.9.]. Hence, w.l.o.g.
$h$
by [Reference Jacobson18, Theorem 1.2.9.]. Hence, w.l.o.g.
![]() $g=f_1 f_2\cdots f_l$
, where the
$g=f_1 f_2\cdots f_l$
, where the
![]() $f_i$
are irreducible in
$f_i$
are irreducible in
![]() $R$
and
$R$
and
![]() $f_i$
is similar to
$f_i$
is similar to
![]() $f$
for all
$f$
for all
![]() $i=1,2,\dots,l$
[Reference Jacobson18, Theorem 1.2.19]. Thus by Lemma 2, the minimal central left multiple of each
$i=1,2,\dots,l$
[Reference Jacobson18, Theorem 1.2.19]. Thus by Lemma 2, the minimal central left multiple of each
![]() $f_i$
is equal to
$f_i$
is equal to
![]() $h$
. Since
$h$
. Since
![]() $f$
is monic, we may assume w.l.o.g. that all
$f$
is monic, we may assume w.l.o.g. that all
![]() $f_i$
are monic. By Theorem 10 and since all
$f_i$
are monic. By Theorem 10 and since all
![]() $f_i\in E[t;\;\sigma ]$
by our assumption, this implies that
$f_i\in E[t;\;\sigma ]$
by our assumption, this implies that
![]() $N_{E/F}(f_i(0))=(\!-\!1)^{dm(n-1)}N_{E/C}(u)^{m}h_0=N_{E/F}(a_0)$
. As the constant term of
$N_{E/F}(f_i(0))=(\!-\!1)^{dm(n-1)}N_{E/C}(u)^{m}h_0=N_{E/F}(a_0)$
. As the constant term of
![]() $g$
is equal to
$g$
is equal to
![]() $\prod _{i=1}^l f_i(0)$
, we see that
$\prod _{i=1}^l f_i(0)$
, we see that
 \begin{align*}N_{E/F}(g_0)&=\prod _{i=1}^l N_{E/F}(f_i(0))=[ (\!-\!1)^{dm(n-1)}N_{E/C}(u)^{m}h_0]^l\\[2pt] &=(\!-\!1)^{l dm(n-1)}N_{E/C}(u)^{lm}h_0^l=N_{E/F}(a_0)^l.\end{align*}
\begin{align*}N_{E/F}(g_0)&=\prod _{i=1}^l N_{E/F}(f_i(0))=[ (\!-\!1)^{dm(n-1)}N_{E/C}(u)^{m}h_0]^l\\[2pt] &=(\!-\!1)^{l dm(n-1)}N_{E/C}(u)^{lm}h_0^l=N_{E/F}(a_0)^l.\end{align*}
We are not able to say if the assumptions on the
![]() $f_i$
’s in the above result are empty or trivial.
$f_i$
’s in the above result are empty or trivial.
5.2. The algebra
 $(\boldsymbol{{K}}(\boldsymbol{{x}})/\boldsymbol{{F}}(\boldsymbol{{x}}),\widetilde{\boldsymbol\sigma },\boldsymbol{{x}})$
$(\boldsymbol{{K}}(\boldsymbol{{x}})/\boldsymbol{{F}}(\boldsymbol{{x}}),\widetilde{\boldsymbol\sigma },\boldsymbol{{x}})$
Let
![]() $K/F$
be a cyclic field extension of degree
$K/F$
be a cyclic field extension of degree
![]() $n$
with
$n$
with
![]() $\textrm{Gal}(K/F)=\langle \sigma \rangle$
,
$\textrm{Gal}(K/F)=\langle \sigma \rangle$
,
![]() $R=K[t;\;\sigma ]$
and
$R=K[t;\;\sigma ]$
and
![]() $x=t^n$
. We now look at the cyclic algebra
$x=t^n$
. We now look at the cyclic algebra
![]() $(K(x)/F(x),\widetilde{\sigma },x)$
(this case corresponds to
$(K(x)/F(x),\widetilde{\sigma },x)$
(this case corresponds to
![]() $D=C$
in the previous Section). Let
$D=C$
in the previous Section). Let
![]() $N$
be the reduced norm of
$N$
be the reduced norm of
![]() $(K(x)/F(x),\widetilde{\sigma },x)$
over
$(K(x)/F(x),\widetilde{\sigma },x)$
over
![]() $F(x)$
(cf. also [Reference Jacobson18, Proposition 1.4.6]). We have
$F(x)$
(cf. also [Reference Jacobson18, Proposition 1.4.6]). We have
![]() $\widetilde{\sigma }|_K=\sigma$
, and
$\widetilde{\sigma }|_K=\sigma$
, and
![]() $N$
is a nondegenerate form of degree
$N$
is a nondegenerate form of degree
![]() $n$
. Let
$n$
. Let
![]() $f=\sum _{i=0}^ma_it^i\in R$
be a polynomial of degree
$f=\sum _{i=0}^ma_it^i\in R$
be a polynomial of degree
![]() $m$
such that
$m$
such that
![]() $a_0\not =0$
and
$a_0\not =0$
and
![]() $h\in R$
be the minimal central left multiple of
$h\in R$
be the minimal central left multiple of
![]() $f$
in
$f$
in
![]() $R$
. Then
$R$
. Then
![]() $N(f(t))=N_{K/F}(a_0)+\dots + (\!-\!1)^{m(n-1)}N_{K/F}(a_m)x^m$
[Reference Thompson and Pumplün36, Theorem 3].
$N(f(t))=N_{K/F}(a_0)+\dots + (\!-\!1)^{m(n-1)}N_{K/F}(a_m)x^m$
[Reference Thompson and Pumplün36, Theorem 3].
Theorem 12.
Suppose that
![]() $\textrm{deg}(h)=mn$
.
$\textrm{deg}(h)=mn$
.
-
(i) [Reference Thompson and Pumplün36, Theorem 6 (i)] If
 $\hat{h}$
is irreducible in
$\hat{h}$
is irreducible in
 $F[x]$
, then
$F[x]$
, then
 $f$
is irreducible in
$f$
is irreducible in
 $R$
.
$R$
. -
(ii) [Reference Thompson and Pumplün36, Theorem 6 (ii)] If
 $f$
is irreducible, then
$f$
is irreducible, then
 $N(f)$
is irreducible in
$N(f)$
is irreducible in
 $F[x]$
.
$F[x]$
. -
(iii)
 $N_{K/F}(a_0)=(\!-\!1)^{m(n-1)}h_0,$
if
$N_{K/F}(a_0)=(\!-\!1)^{m(n-1)}h_0,$
if
 $h_0$
denotes the constant term of
$h_0$
denotes the constant term of
 $\hat{h}$
.
$\hat{h}$
.
Theorem 12 (iii) is proved analogously as Theorem 10 (iii).
Theorem 13 (cf. [Reference Sheekey34, Theorem 5] for finite fields, the proof is the same). Suppose that
![]() $f$
is not right-invariant. If
$f$
is not right-invariant. If
![]() $\textrm{deg}(h)=mn$
and
$\textrm{deg}(h)=mn$
and
![]() $g$
is a monic divisor of
$g$
is a monic divisor of
![]() $h(t)$
in
$h(t)$
in
![]() $R$
of degree
$R$
of degree
![]() $ml$
, then
$ml$
, then
6. Division algebras and MRD codes employing
 $\boldsymbol{{f}}\boldsymbol\in \boldsymbol{{R}}$
$\boldsymbol{{f}}\boldsymbol\in \boldsymbol{{R}}$
6.1. The case that f
 $\in$
D[t;
$\in$
D[t;
 $\sigma$
]
$\sigma$
]
Let
![]() $f\in R=D[t;\;\sigma ]$
be a monic polynomial of degree
$f\in R=D[t;\;\sigma ]$
be a monic polynomial of degree
![]() $m$
. Let
$m$
. Let
![]() $\rho \in \textrm{Aut }(D)$
,
$\rho \in \textrm{Aut }(D)$
,
![]() $\nu \in D$
and
$\nu \in D$
and
![]() $F'=\textrm{Fix}(\rho )\cap F$
where
$F'=\textrm{Fix}(\rho )\cap F$
where
![]() $F=C\cap \textrm{Fix}(\sigma )$
. Let
$F=C\cap \textrm{Fix}(\sigma )$
. Let
![]() $b(t), c(t)\in R_m=\{g\in R\,|\, \textrm{deg}(g)\lt m\}$
and
$b(t), c(t)\in R_m=\{g\in R\,|\, \textrm{deg}(g)\lt m\}$
and
![]() $b_0$
be the constant term of
$b_0$
be the constant term of
![]() $b(t)$
. Then, the multiplication defined via
$b(t)$
. Then, the multiplication defined via
makes
![]() $R_m$
into a non-unital nonassociative ring
$R_m$
into a non-unital nonassociative ring
![]() $(R_m,\circ )$
. When the context is clear, we will drop the
$(R_m,\circ )$
. When the context is clear, we will drop the
![]() $\circ$
notation and simply use juxtaposition.
$\circ$
notation and simply use juxtaposition.
![]() $(R_m,\circ )$
is an algebra over
$(R_m,\circ )$
is an algebra over
![]() $F'$
.
$F'$
.
Example 14.
If
![]() $f(t)=t-c\in D[t;\;\sigma ]$
for some
$f(t)=t-c\in D[t;\;\sigma ]$
for some
![]() $c\in D$
,
$c\in D$
,
![]() $\nu \neq 0$
, then
$\nu \neq 0$
, then
![]() $(R_m,\circ )$
has the multiplication
$(R_m,\circ )$
has the multiplication
 \begin{align*} a\circ b&=(a+\nu\rho(a)t)b)\hspace{0.222em}\hspace{0.167em}\hspace{0.167em}{\text{mod}}_rf\\[5pt] &=ab+\nu\rho(a)\sigma(b)t\hspace{0.222em}\hspace{0.167em}\hspace{0.167em}{\text{mod}}_rf\\[5pt] &=ab+\nu\rho(a)\sigma(b)c,\end{align*}
\begin{align*} a\circ b&=(a+\nu\rho(a)t)b)\hspace{0.222em}\hspace{0.167em}\hspace{0.167em}{\text{mod}}_rf\\[5pt] &=ab+\nu\rho(a)\sigma(b)t\hspace{0.222em}\hspace{0.167em}\hspace{0.167em}{\text{mod}}_rf\\[5pt] &=ab+\nu\rho(a)\sigma(b)c,\end{align*}
for all
![]() $a,b\in D$
. This generalizes the algebras studied in [Reference Pumplün30]. If
$a,b\in D$
. This generalizes the algebras studied in [Reference Pumplün30]. If
![]() $R=K[t;\;\sigma ]$
for some finite field extension
$R=K[t;\;\sigma ]$
for some finite field extension
![]() $K/F$
; this is the multiplication of Albert’s twisted semifields [Reference Albert1]. If
$K/F$
; this is the multiplication of Albert’s twisted semifields [Reference Albert1]. If
![]() $F/F'$
is finite and
$F/F'$
is finite and
![]() $(R_m,\circ )$
is not a division algebra,
$(R_m,\circ )$
is not a division algebra,
![]() $a\circ b=0$
for some nonzero
$a\circ b=0$
for some nonzero
![]() $a,b\in D$
, if and only if
$a,b\in D$
, if and only if
![]() $ ab=-\nu \rho (a)\sigma (b)c$
. Taking norms of both sides and canceling
$ ab=-\nu \rho (a)\sigma (b)c$
. Taking norms of both sides and canceling
![]() $N_{D/F'}(ab)$
on both sides, we obtain that
$N_{D/F'}(ab)$
on both sides, we obtain that
![]() $N_{D/F'}(\!-\!\nu c)=(\!-\!1)^{d^2n[F\;:\;F']} N_{D/F'}(\nu c)=1.$
Thus, if
$N_{D/F'}(\!-\!\nu c)=(\!-\!1)^{d^2n[F\;:\;F']} N_{D/F'}(\nu c)=1.$
Thus, if
![]() $F/F'$
is finite and
$F/F'$
is finite and
![]() $N_{D/F'}(\nu c)\neq (\!-\!1)^{d^2n[F\;:\;F']}$
then
$N_{D/F'}(\nu c)\neq (\!-\!1)^{d^2n[F\;:\;F']}$
then
![]() $(R_m,\circ )$
is a division algebra.
$(R_m,\circ )$
is a division algebra.
From now on for the rest of the paper, we again assume that
![]() $f$
is an irreducible monic polynomial of degree
$f$
is an irreducible monic polynomial of degree
![]() $m\gt 1$
,
$m\gt 1$
,
![]() $(f,t)_r= 1$
, and that
$(f,t)_r= 1$
, and that
![]() $h$
is the minimal central left multiple of
$h$
is the minimal central left multiple of
![]() $f$
. Let
$f$
. Let
![]() $F/F'$
be finite-dimensional, and
$F/F'$
be finite-dimensional, and
Theorem 15.
Let
![]() $l=1$
. Then:
$l=1$
. Then:
-
(i) Let
 $b(t)\in R_m$
with constant coefficient
$b(t)\in R_m$
with constant coefficient
 $b_0$
. If
$b_0$
. If
 $b(t)+\nu \rho (b_0)t^m\in P$
is reducible in
$b(t)+\nu \rho (b_0)t^m\in P$
is reducible in
 $R$
, then
$R$
, then
 $b(t)$
is not a left zero divisor in
$b(t)$
is not a left zero divisor in
 $(R_m, \circ )$
.
$(R_m, \circ )$
. -
(ii) If
 $\nu =0$
, then
$\nu =0$
, then
 $(R_m, \circ )$
is a division algebra over
$(R_m, \circ )$
is a division algebra over
 $F'$
, which for
$F'$
, which for
 $m\geq 2$
is a Petit algebra.
$m\geq 2$
is a Petit algebra.
-
(iii) If
 $P$
does not contain any polynomial similar to
$P$
does not contain any polynomial similar to
 $f$
, then
$f$
, then
 $(R_m, \circ )$
is a division algebra over
$(R_m, \circ )$
is a division algebra over
 $F'$
.
$F'$
.
Note that
![]() $f$
may be right-invariant.
$f$
may be right-invariant.
Proof. Suppose that there are
![]() $b(t)=b_0+b_1t+\dots +b_{m-1}t^{m-1}, c(t)\in R_m$
, such that
$b(t)=b_0+b_1t+\dots +b_{m-1}t^{m-1}, c(t)\in R_m$
, such that
Then, there exists
![]() $g\in R_m$
such that
$g\in R_m$
such that
![]() $(b(t)+\nu \rho (b_0)t^m) c(t)=g(t)f(t).$
Since
$(b(t)+\nu \rho (b_0)t^m) c(t)=g(t)f(t).$
Since
![]() $f$
is irreducible and of degree
$f$
is irreducible and of degree
![]() $m$
, while
$m$
, while
![]() $deg(c) \lt m$
,
$deg(c) \lt m$
,
![]() $f$
must be similar to an irreducible factor of
$f$
must be similar to an irreducible factor of
![]() $b(t)+\nu \rho (b_0)t^m$
, because of the uniqueness of an irreducible decomposition in
$b(t)+\nu \rho (b_0)t^m$
, because of the uniqueness of an irreducible decomposition in
![]() $R$
up to similarity. But
$R$
up to similarity. But
![]() $b(t)+\nu \rho (b_0)t^m$
has degree at most
$b(t)+\nu \rho (b_0)t^m$
has degree at most
![]() $m$
, so
$m$
, so
![]() $f$
is similar to
$f$
is similar to
![]() $b(t)+\nu \rho (b_0)t^m$
. Thus,
$b(t)+\nu \rho (b_0)t^m$
. Thus,
![]() $b(t)+\nu \rho (b_0)t^m$
must have degree
$b(t)+\nu \rho (b_0)t^m$
must have degree
![]() $m$
and be irreducible as well. Hence if
$m$
and be irreducible as well. Hence if
![]() $b(t)+\nu \rho (b_0)t^m$
is not similar to
$b(t)+\nu \rho (b_0)t^m$
is not similar to
![]() $f$
then
$f$
then
![]() $b(t)+\nu \rho (b_0)t^m$
is not a left zero divisor in
$b(t)+\nu \rho (b_0)t^m$
is not a left zero divisor in
![]() $(R_m, \circ )$
. This happens for instance, if
$(R_m, \circ )$
. This happens for instance, if
![]() $\nu =0$
or if
$\nu =0$
or if
![]() $b(t)+\nu \rho (b_0)t^m$
is reducible. Moreover,
$b(t)+\nu \rho (b_0)t^m$
is reducible. Moreover,
![]() $(R_m, \circ )$
is a division algebra if
$(R_m, \circ )$
is a division algebra if
![]() $P$
does not contain any polynomial similar to
$P$
does not contain any polynomial similar to
![]() $f$
.
$f$
.
We are again not able to say if the assumptions on the
![]() $f_i$
’s in the following result are empty or trivial.
$f_i$
’s in the following result are empty or trivial.
Theorem 16.
Let
![]() $D=(E/C,\gamma,a)$
be a cyclic division algebra over
$D=(E/C,\gamma,a)$
be a cyclic division algebra over
![]() $C$
of degree
$C$
of degree
![]() $d$
such that
$d$
such that
![]() $\sigma |_E\in \textrm{Aut}(E)$
and
$\sigma |_E\in \textrm{Aut}(E)$
and
![]() $\gamma \circ \sigma |_E=\sigma |_E\circ \gamma$
. Suppose that
$\gamma \circ \sigma |_E=\sigma |_E\circ \gamma$
. Suppose that
![]() $\sigma ^n(z)=u^{-1}zu$
with
$\sigma ^n(z)=u^{-1}zu$
with
![]() $u\in E$
.
$u\in E$
.
Let
![]() $f(t)=\sum _{i=0}^ma_it^i\in E[t;\;\sigma ]\subset D[t;\;\sigma ]$
be monic and irreducible, and let
$f(t)=\sum _{i=0}^ma_it^i\in E[t;\;\sigma ]\subset D[t;\;\sigma ]$
be monic and irreducible, and let
![]() $\textrm{deg}(h)=dmn$
. Suppose that all monic
$\textrm{deg}(h)=dmn$
. Suppose that all monic
![]() $f_i$
similar to
$f_i$
similar to
![]() $f$
lie in
$f$
lie in
![]() $E[t;\;\sigma ]$
. Then,
$E[t;\;\sigma ]$
. Then,
![]() $(R_m, \circ )$
is a division algebra over
$(R_m, \circ )$
is a division algebra over
![]() $F'$
, if one of the following holds: (i)
$F'$
, if one of the following holds: (i)
![]() $\nu \not \in E$
and
$\nu \not \in E$
and
![]() $\rho |_E\in \textrm{Aut}(E)$
. (ii)
$\rho |_E\in \textrm{Aut}(E)$
. (ii)
![]() $\nu \in E^\times$
and
$\nu \in E^\times$
and
![]() $\rho |_E\in \textrm{Aut}(E)$
, such that
$\rho |_E\in \textrm{Aut}(E)$
, such that
Note that our global assumption that
![]() $\sigma ^n(z)=u^{-1}zu$
for all
$\sigma ^n(z)=u^{-1}zu$
for all
![]() $z\in D$
, so that
$z\in D$
, so that
![]() $\sigma ^n(e)=u^{-1}eu=e$
for all
$\sigma ^n(e)=u^{-1}eu=e$
for all
![]() $e\in E$
, forces
$e\in E$
, forces
![]() $(\sigma |_E)^n=id$
.
$(\sigma |_E)^n=id$
.
Proof. By Theorem 15,
![]() $(R_m, \circ )$
is a division algebra, if the set
$(R_m, \circ )$
is a division algebra, if the set
![]() $P$
with
$P$
with
![]() $l=1$
does not contain any polynomial similar to
$l=1$
does not contain any polynomial similar to
![]() $f$
. All polynomials similar to
$f$
. All polynomials similar to
![]() $f$
are irreducible factors of
$f$
are irreducible factors of
![]() $h(t)$
, so
$h(t)$
, so
![]() $(R_m, \circ )$
is a division algebra, if
$(R_m, \circ )$
is a division algebra, if
![]() $P$
does not contain any irreducible factor of
$P$
does not contain any irreducible factor of
![]() $h(t)$
. Suppose that
$h(t)$
. Suppose that
![]() $P$
contains an irreducible factor
$P$
contains an irreducible factor
![]() $g$
of
$g$
of
![]() $h$
with constant term
$h$
with constant term
![]() $g_0$
. Then,
$g_0$
. Then,
![]() $g$
has degree
$g$
has degree
![]() $m$
as it is similar to
$m$
as it is similar to
![]() $f$
. Let
$f$
. Let
![]() $g_{m} t^{m}$
be its highest coefficient, so that
$g_{m} t^{m}$
be its highest coefficient, so that
![]() $g_{m}^{-1}g$
is a monic divisor of
$g_{m}^{-1}g$
is a monic divisor of
![]() $h$
.
$h$
.
By Theorem 10 and since
![]() $g\in E[t;\;\sigma ]$
by assumption, this implies
$g\in E[t;\;\sigma ]$
by assumption, this implies
and in particular, that
![]() $g_0$
and
$g_0$
and
![]() $g_m$
are both nonzero. Since
$g_m$
are both nonzero. Since
![]() $g\in P$
, we also have
$g\in P$
, we also have
![]() $g_{m}=\nu \rho (g_0)$
. Suppose
$g_{m}=\nu \rho (g_0)$
. Suppose
![]() $\nu \not \in E$
and
$\nu \not \in E$
and
![]() $\rho (E)\subset E$
. Since the coefficients of the
$\rho (E)\subset E$
. Since the coefficients of the
![]() $f_i$
all lie in
$f_i$
all lie in
![]() $E$
, we have
$E$
, we have
![]() $g_{m}\not =\nu \rho (g_0)$
which yields a contradiction. Hence, there is no divisor
$g_{m}\not =\nu \rho (g_0)$
which yields a contradiction. Hence, there is no divisor
![]() $g$
of
$g$
of
![]() $h$
in
$h$
in
![]() $P$
and
$P$
and
![]() $S$
is a division algebra. Suppose that
$S$
is a division algebra. Suppose that
![]() $\nu \in E^\times$
and
$\nu \in E^\times$
and
![]() $\rho (E)\subset E$
. Substituting
$\rho (E)\subset E$
. Substituting
![]() $g_{m}=\nu \rho (g_0)$
into the above equation yields
$g_{m}=\nu \rho (g_0)$
into the above equation yields
Applying
![]() $N_{F/F'}$
to both sides implies that
$N_{F/F'}$
to both sides implies that
Now
![]() $N_{E/F'}(\rho (g_0))=N_{E/F'}(g_0)$
, so we can cancel the nonzero term
$N_{E/F'}(\rho (g_0))=N_{E/F'}(g_0)$
, so we can cancel the nonzero term
![]() $N_{E/F'}(g_0)$
to obtain
$N_{E/F'}(g_0)$
to obtain
![]() $1=N_{E/F'}(a_0)$
$1=N_{E/F'}(a_0)$
![]() $N_{E/F'}(\nu ).$
$N_{E/F'}(\nu ).$
Remark 17.
Let
![]() $S=S_{n,m,1}(\nu,\rho, f)=\lbrace a+Rh\,|\, a\in P\rbrace$
. We can use
$S=S_{n,m,1}(\nu,\rho, f)=\lbrace a+Rh\,|\, a\in P\rbrace$
. We can use
![]() $\mathcal{C}(S)\subset M_k(B)$
to define a multiplication on
$\mathcal{C}(S)\subset M_k(B)$
to define a multiplication on
![]() $B^m$
. As
$B^m$
. As
![]() $\textrm{dim}_F(D)=d^2n$
and
$\textrm{dim}_F(D)=d^2n$
and
![]() $\textrm{dim}_F(B)=d^2mn/k$
, there exists an
$\textrm{dim}_F(B)=d^2mn/k$
, there exists an
![]() $F$
-vector space isomorphism between
$F$
-vector space isomorphism between
![]() $D^m$
and
$D^m$
and
![]() $B^k$
. Similarly, there exists an isomorphism
$B^k$
. Similarly, there exists an isomorphism
![]() $G\;:\;V_f\to B^k$
,
$G\;:\;V_f\to B^k$
,
![]() $G(a+Rf)=\underline{a}$
. Define
$G(a+Rf)=\underline{a}$
. Define
![]() $\ast\;:\;B^k\times B^k\to B^k$
by
$\ast\;:\;B^k\times B^k\to B^k$
by
for all
![]() $\underline{a},\underline{b}\in B^k$
, where
$\underline{a},\underline{b}\in B^k$
, where
![]() $M_a\in \mathcal{C}(S)$
is the representation of the map
$M_a\in \mathcal{C}(S)$
is the representation of the map
![]() $L_{a(t)+\nu \rho (a_0)t^m}\in \textrm{End}_B(R/Rf)$
induced by
$L_{a(t)+\nu \rho (a_0)t^m}\in \textrm{End}_B(R/Rf)$
induced by
![]() $G$
. (Each
$G$
. (Each
![]() $a\in R_m$
corresponds to a map
$a\in R_m$
corresponds to a map
![]() $L_{a(t)+\nu \rho (a_0)t^m}$
. As
$L_{a(t)+\nu \rho (a_0)t^m}$
. As
![]() $\textrm{End}_B(R/Rf)\cong M_k(B)$
and
$\textrm{End}_B(R/Rf)\cong M_k(B)$
and
![]() $\textrm{dim}(R_m)=\textrm{dim}(\mathcal{C}(S))$
, there is a canonical bijection between
$\textrm{dim}(R_m)=\textrm{dim}(\mathcal{C}(S))$
, there is a canonical bijection between
![]() $L_{a(t)+\nu \rho (a_0)t^m}$
and
$L_{a(t)+\nu \rho (a_0)t^m}$
and
![]() $M_a$
.) As
$M_a$
.) As
![]() $M_a$
represents
$M_a$
represents
![]() $L_a\in \text{End}_B(R/Rf)$
,
$L_a\in \text{End}_B(R/Rf)$
,
![]() $(B^k,\ast )$
is isomorphic to
$(B^k,\ast )$
is isomorphic to
![]() $R/Rf$
equipped with the multiplication
$R/Rf$
equipped with the multiplication
![]() $(a+Rf)(b+Rf)=L_{a(t)+\nu \rho (a_0)t^m}(b+Rf)$
. Thus,
$(a+Rf)(b+Rf)=L_{a(t)+\nu \rho (a_0)t^m}(b+Rf)$
. Thus,
![]() $(R_m,\circ )$
and
$(R_m,\circ )$
and
![]() $(B^k,\ast )$
are isomorphic algebras and
$(B^k,\ast )$
are isomorphic algebras and
![]() $S_{n,m,1}(\nu,\rho, f)$
is the same algebra as
$S_{n,m,1}(\nu,\rho, f)$
is the same algebra as
![]() $(R_m, \circ )$
.
$(R_m, \circ )$
.
If
![]() $l=1$
, we write
$l=1$
, we write
![]() $S(\nu,\rho, f)=S_{n,m,1}(\nu,\rho, f)$
for
$S(\nu,\rho, f)=S_{n,m,1}(\nu,\rho, f)$
for
![]() $(R_m,\circ )$
.
$(R_m,\circ )$
.
![]() $S(\nu,\rho, f)$
is a division algebra if and only if every matrix in
$S(\nu,\rho, f)$
is a division algebra if and only if every matrix in
![]() $\mathcal{C}_{n,m,1}$
has full column rank. It then canonically defines an
$\mathcal{C}_{n,m,1}$
has full column rank. It then canonically defines an
![]() $F'$
-linear
$F'$
-linear
![]() $MRD$
code in
$MRD$
code in
![]() $M_k(B)$
,
$M_k(B)$
,
![]() $B=\textrm{Nuc}_r(S_f)$
. Therefore, we obtain from all of the above results:
$B=\textrm{Nuc}_r(S_f)$
. Therefore, we obtain from all of the above results:
Corollary 18.
Let
![]() $D=(E/C,\gamma,a)$
be a cyclic division algebra over
$D=(E/C,\gamma,a)$
be a cyclic division algebra over
![]() $C$
of degree
$C$
of degree
![]() $d$
such that
$d$
such that
![]() $\sigma |_E\in \textrm{Aut}(E)$
and
$\sigma |_E\in \textrm{Aut}(E)$
and
![]() $\gamma \circ \sigma =\sigma \circ \gamma$
. Suppose that
$\gamma \circ \sigma =\sigma \circ \gamma$
. Suppose that
![]() $\sigma ^n(z)=u^{-1}zu$
with
$\sigma ^n(z)=u^{-1}zu$
with
![]() $u\in E$
.
$u\in E$
.
Let
![]() $f=\sum _{i=0}^ma_it^i\in R$
be monic and irreducible of degree
$f=\sum _{i=0}^ma_it^i\in R$
be monic and irreducible of degree
![]() $m$
. Then,
$m$
. Then,
![]() $B$
is a division algebra over
$B$
is a division algebra over
![]() $E_{\hat{h}}$
and
$E_{\hat{h}}$
and
![]() $S(\nu,\rho, f)$
defines an
$S(\nu,\rho, f)$
defines an
![]() $F'$
-linear MRD code in
$F'$
-linear MRD code in
![]() $M_k(B)$
with minimum distance
$M_k(B)$
with minimum distance
![]() $k$
, if one of the following holds:
$k$
, if one of the following holds:
-
(i)
 $\nu =0$
. Then,
$\nu =0$
. Then,
 $S(\nu,\rho, f)$
is a (unital) Petit algebra.
$S(\nu,\rho, f)$
is a (unital) Petit algebra.
-
(ii)
 $P$
does not contain any polynomial similar to
$P$
does not contain any polynomial similar to
 $f$
.
$f$
. -
(iii) Suppose
 $\rho |_E\in \textrm{Aut}(E)$
,
$\rho |_E\in \textrm{Aut}(E)$
,
 $f=\sum _{i=0}^ma_it^i\in E[t;\;\sigma ]\subset R$
,
$f=\sum _{i=0}^ma_it^i\in E[t;\;\sigma ]\subset R$
,
 $\textrm{deg}(h)=dmn$
, all the monic polynomials similar to
$\textrm{deg}(h)=dmn$
, all the monic polynomials similar to
 $f$
lie in
$f$
lie in
 $E[t;\;\sigma ]$
, and one of the following holds:
$E[t;\;\sigma ]$
, and one of the following holds:
-
(a)
 $\nu \not \in E$
,
$\nu \not \in E$
, -
(b)
 $N_{E/F'}(\nu )N_{E/F'}(a_0)\neq 1.$
Then, we get an
$N_{E/F'}(\nu )N_{E/F'}(a_0)\neq 1.$
Then, we get an
 $F'$
-linear MRD code in
$F'$
-linear MRD code in
 $M_{dn}(E_{\hat{h}})$
with minimum distance
$M_{dn}(E_{\hat{h}})$
with minimum distance
 $dn$
.
$dn$
.
The case
![]() $\nu =0$
produces the MRD codes which are associated with the unital Petit algebras. They can be viewed as generalized Gabidulin codes.
$\nu =0$
produces the MRD codes which are associated with the unital Petit algebras. They can be viewed as generalized Gabidulin codes.
More generally, we can also construct MRD codes for
![]() $l\gt 1$
. Let
$l\gt 1$
. Let
![]() $f\in R$
not be right-invariant, and let
$f\in R$
not be right-invariant, and let
![]() $l\lt k$
be a positive integer.
$l\lt k$
be a positive integer.
Theorem 19.
Suppose that
![]() $P$
does not contain any polynomial of degree
$P$
does not contain any polynomial of degree
![]() $lm$
, whose irreducible factors are all similar to
$lm$
, whose irreducible factors are all similar to
![]() $f$
. Then, the set
$f$
. Then, the set
![]() $S_{n,m,l}(\nu,\rho, f)$
defines an
$S_{n,m,l}(\nu,\rho, f)$
defines an
![]() $F'$
-linear MRD code in
$F'$
-linear MRD code in
![]() $M_k(B)$
with minimum distance
$M_k(B)$
with minimum distance
![]() $k-l+1$
. In particular, if
$k-l+1$
. In particular, if
![]() $\textrm{deg}(h)=dmn$
, then this code is an
$\textrm{deg}(h)=dmn$
, then this code is an
![]() $F'$
-linear MRD code in
$F'$
-linear MRD code in
![]() $M_{dn}(E_{\hat{h}})$
with minimum distance
$M_{dn}(E_{\hat{h}})$
with minimum distance
![]() $dn-l+1$
.
$dn-l+1$
.
We are not able to say if the assumption on
![]() $P$
can be satisfied in this general setup. It is satisfied in the case considered in [Reference Sheekey34, Theorem 7].
$P$
can be satisfied in this general setup. It is satisfied in the case considered in [Reference Sheekey34, Theorem 7].
Proof. We have to show that the minimum column rank of the matrix corresponding to a nonzero element in
![]() $S_{n,m,l}(\nu,\rho, f)$
is
$S_{n,m,l}(\nu,\rho, f)$
is
![]() $k-l+1$
. By Theorem 6, this is equivalent to finding an element
$k-l+1$
. By Theorem 6, this is equivalent to finding an element
![]() $g\in A$
such that the greatest common right divisor of
$g\in A$
such that the greatest common right divisor of
![]() $g$
and
$g$
and
![]() $h$
has degree at most
$h$
has degree at most
![]() $(l-1)m$
. Suppose towards a contradiction that there exists
$(l-1)m$
. Suppose towards a contradiction that there exists
![]() $g\in A$
such that
$g\in A$
such that
![]() $\textrm{deg}(\textrm{gcrd}(g,h))=lm$
; since
$\textrm{deg}(\textrm{gcrd}(g,h))=lm$
; since
![]() $\textrm{deg}(g)\leq lm$
, it follows that
$\textrm{deg}(g)\leq lm$
, it follows that
![]() $g$
must be a divisor of
$g$
must be a divisor of
![]() $h$
. As any divisor of
$h$
. As any divisor of
![]() $h$
is a product of irreducible polynomials similar to
$h$
is a product of irreducible polynomials similar to
![]() $f$
,
$f$
,
![]() $g$
must be a product of polynomials similar to
$g$
must be a product of polynomials similar to
![]() $f$
. This contradicts our assumption, so any matrix has rank at least
$f$
. This contradicts our assumption, so any matrix has rank at least
![]() $k-l+1$
.
$k-l+1$
.
Theorem 20 (for
![]() $f\in K[t;\;\sigma ]$
,
$f\in K[t;\;\sigma ]$
,
![]() $K$
a finite field, this is [Reference Sheekey34, Theorem 7]). Let
$K$
a finite field, this is [Reference Sheekey34, Theorem 7]). Let
![]() $f=\sum _{i=0}^ma_it^i \in E[t;\;\sigma ]\subset R=D[t;\;\sigma ]$
be monic irreducible, and let
$f=\sum _{i=0}^ma_it^i \in E[t;\;\sigma ]\subset R=D[t;\;\sigma ]$
be monic irreducible, and let
![]() $\textrm{deg}(h)=dmn$
. Suppose that all monic
$\textrm{deg}(h)=dmn$
. Suppose that all monic
![]() $f_i$
similar to
$f_i$
similar to
![]() $f$
lie in
$f$
lie in
![]() $E[t;\;\sigma ]$
. Then,
$E[t;\;\sigma ]$
. Then,
![]() $S_{n,m,l}(\nu,\rho, f)$
defines an
$S_{n,m,l}(\nu,\rho, f)$
defines an
![]() $F'$
-linear MRD code in
$F'$
-linear MRD code in
![]() $M_{dn}(E_{\hat{h}})$
with minimum distance
$M_{dn}(E_{\hat{h}})$
with minimum distance
![]() $dn-l+1$
, if one of the following holds:
$dn-l+1$
, if one of the following holds:
-
(i)
 $\nu =0$
$\nu =0$
-
(ii)
 $\nu \not \in E$
and
$\nu \not \in E$
and
 $\rho |_E\in \textrm{Aut}(E)$
.
$\rho |_E\in \textrm{Aut}(E)$
. -
(iii)
 $\nu \in E$
,
$\nu \in E$
,
 $\rho |_E\in \textrm{Aut}(E)$
and
$\rho |_E\in \textrm{Aut}(E)$
and
 $N_{E/F'}(\nu )N_{E/F'}(a_0)^l\neq 1.$
$N_{E/F'}(\nu )N_{E/F'}(a_0)^l\neq 1.$
The proof is straightforward.
6.2. The case R = K[t;
 $\sigma$
]
$\sigma$
]
Let
![]() $f=\sum _{i=0}^ma_it^i\in R=K[t;\;\sigma ]$
be an irreducible monic polynomial of degree
$f=\sum _{i=0}^ma_it^i\in R=K[t;\;\sigma ]$
be an irreducible monic polynomial of degree
![]() $m$
with minimal central left multiple
$m$
with minimal central left multiple
![]() $h$
. Suppose throughout this section that
$h$
. Suppose throughout this section that
![]() $F/F'$
is a finite field extension,
$F/F'$
is a finite field extension,
![]() $\nu \in K$
, and
$\nu \in K$
, and
![]() $\rho \in \textrm{Aut}(K)$
. Let
$\rho \in \textrm{Aut}(K)$
. Let
![]() $1\lt l\lt k$
and
$1\lt l\lt k$
and
![]() $S_{n,m,l}(\nu,\rho, f)=\lbrace a+Rh\,|\, a\in P\rbrace \subset R/Rh,$
where
$S_{n,m,l}(\nu,\rho, f)=\lbrace a+Rh\,|\, a\in P\rbrace \subset R/Rh,$
where
![]() $P=\lbrace d_0+d_1t+\dots +d_{lm-1}t^{lm-1}+\nu \rho (d_0)t^{lm}\,|\, d_i\in K \rbrace .$
Then, we obtain the following results:
$P=\lbrace d_0+d_1t+\dots +d_{lm-1}t^{lm-1}+\nu \rho (d_0)t^{lm}\,|\, d_i\in K \rbrace .$
Then, we obtain the following results:
Theorem 21.
Let
![]() $l=1$
.
$l=1$
.
-
(i) Let
 $b(t)\in R_m$
with constant coefficient
$b(t)\in R_m$
with constant coefficient
 $b_0$
. If
$b_0$
. If
 $b(t)+\nu \rho (b_0)t^m\in P$
is reducible in
$b(t)+\nu \rho (b_0)t^m\in P$
is reducible in
 $R$
, then
$R$
, then
 $b(t)$
is not a left zero divisor in
$b(t)$
is not a left zero divisor in
 $S(\nu,\rho, f)$
.
$S(\nu,\rho, f)$
. -
(ii) If
 $\nu =0$
, then
$\nu =0$
, then
 $S(\nu,\rho, f)$
is a division algebra over
$S(\nu,\rho, f)$
is a division algebra over
 $F'$
, a unital Petit algebra.
$F'$
, a unital Petit algebra.
-
(iii) If
 $P$
does not contain any polynomial similar to
$P$
does not contain any polynomial similar to
 $f$
, then
$f$
, then
 $S(\nu,\rho, f)$
is a division algebra over
$S(\nu,\rho, f)$
is a division algebra over
 $F'$
.
$F'$
.
The proof is analogous to the one of Theorem 15. Note that
![]() $f$
may be right-invariant here. Using Theorems 10 and 13, we obtain (for finite fields, cf. [Reference Sheekey34], the proof is analogous):
$f$
may be right-invariant here. Using Theorems 10 and 13, we obtain (for finite fields, cf. [Reference Sheekey34], the proof is analogous):
Theorem 22.
Suppose that
![]() $\textrm{deg}(h)=mn$
. Then,
$\textrm{deg}(h)=mn$
. Then,
![]() $S(\nu,\rho, f)$
is a division algebra over
$S(\nu,\rho, f)$
is a division algebra over
![]() $F'$
if
$F'$
if
Corollary 23.
![]() $B=\textrm{Nuc}_r(S_f)$
is a division algebra and the left multiplication of the algebra
$B=\textrm{Nuc}_r(S_f)$
is a division algebra and the left multiplication of the algebra
![]() $S(\nu,\rho, f)$
defines an
$S(\nu,\rho, f)$
defines an
![]() $F'$
-linear MRD code in
$F'$
-linear MRD code in
![]() $M_k(B)$
with minimum distance
$M_k(B)$
with minimum distance
![]() $k$
, if one of the following holds:
$k$
, if one of the following holds:
-
(i)
 $\nu =0$
.
$\nu =0$
. -
(ii)
 $P$
does not contain any polynomial similar to
$P$
does not contain any polynomial similar to
 $f$
.
$f$
. -
(iii)
 $\textrm{deg}(h)=mn$
and
$\textrm{deg}(h)=mn$
and
 $\nu \in K$
such that
$\nu \in K$
such that
 $N_{K/F'}(\nu )\neq 1/N_{K/F'}(a_0).$
In this case, the algebra
$N_{K/F'}(\nu )\neq 1/N_{K/F'}(a_0).$
In this case, the algebra
 $S(\nu,\rho, f)$
defines an
$S(\nu,\rho, f)$
defines an
 $F'$
-linear MRD code in
$F'$
-linear MRD code in
 $M_n(E_{\hat{h}})$
with minimum distance
$M_n(E_{\hat{h}})$
with minimum distance
 $n$
.
$n$
.
Note that the condition on
![]() $f$
in (iii) is satisfied for all
$f$
in (iii) is satisfied for all
![]() $f$
if
$f$
if
![]() $gcd(m,n)=1$
or if
$gcd(m,n)=1$
or if
![]() $n$
is prime.
$n$
is prime.
We now look at the case that
![]() $1\lt l\lt k$
and also assume that
$1\lt l\lt k$
and also assume that
![]() $f$
is not right-invariant.
$f$
is not right-invariant.
Theorem 24 (for finite fields, cf. [Reference Sheekey34, Theorem 7]). If
![]() $\textrm{deg}(h)=mn$
, then the set
$\textrm{deg}(h)=mn$
, then the set
![]() $S_{n,m,l}(\nu,\rho, f)$
defines an
$S_{n,m,l}(\nu,\rho, f)$
defines an
![]() $F'$
-linear MRD code in
$F'$
-linear MRD code in
![]() $M_n(E_{\hat{h}})$
with minimum distance
$M_n(E_{\hat{h}})$
with minimum distance
![]() $n-l+1$
for any
$n-l+1$
for any
![]() $\nu \in K$
such that
$\nu \in K$
such that
Note that
![]() $k=n$
here since
$k=n$
here since
![]() $\textrm{deg}(h)=mn$
.
$\textrm{deg}(h)=mn$
.
Corollary 25.
The set
![]() $S_{n,m,l}(\nu,\rho, h)$
defines an
$S_{n,m,l}(\nu,\rho, h)$
defines an
![]() $F'$
-linear MRD code in
$F'$
-linear MRD code in
![]() $M_n(E_{\hat{h}})$
with minimum distance
$M_n(E_{\hat{h}})$
with minimum distance
![]() $n-l+1$
, if one of the following holds:
$n-l+1$
, if one of the following holds:
-
(i)
 $\textrm{deg}(h)=mn$
and
$\textrm{deg}(h)=mn$
and
 $\nu =0$
,
$\nu =0$
, -
(ii)
 $n$
is prime or
$n$
is prime or
 $gcd(m,n)=1$
, and
$gcd(m,n)=1$
, and
 $1\not =N_{K/F'}(\nu )N_{K/F'}(a_0)^l$
$1\not =N_{K/F'}(\nu )N_{K/F'}(a_0)^l$
-
(iii)
 $\textrm{deg}(h)=mn$
and
$\textrm{deg}(h)=mn$
and
 $N_{K/F'}(\nu )\not \in ({F'}^\times )^l$
.
$N_{K/F'}(\nu )\not \in ({F'}^\times )^l$
.
The codes
![]() $S_{n,m,l}(0,\rho, h)$
generalize the Gabidulin codes constructed in [Reference Gabidulin10] that go back to [Reference Delsarte8].
$S_{n,m,l}(0,\rho, h)$
generalize the Gabidulin codes constructed in [Reference Gabidulin10] that go back to [Reference Delsarte8].
Note that
![]() $N_{K/F'}(\nu )\not \in ({F'}^\times )^l$
implies
$N_{K/F'}(\nu )\not \in ({F'}^\times )^l$
implies
![]() $N_{K/F'}(\nu )\not =N_{K/F'}(a_0)^l$
for any
$N_{K/F'}(\nu )\not =N_{K/F'}(a_0)^l$
for any
![]() $f$
. Thus, (ii) implies (iii) above.
$f$
. Thus, (ii) implies (iii) above.
Theorem 26.
Suppose that
![]() $P$
does not contain any polynomial of degree
$P$
does not contain any polynomial of degree
![]() $lm$
, whose irreducible factors are all similar to
$lm$
, whose irreducible factors are all similar to
![]() $f$
. Then the set
$f$
. Then the set
![]() $S_{n,m,l}(\nu,\rho, f)$
defines an
$S_{n,m,l}(\nu,\rho, f)$
defines an
![]() $F'$
-linear MRD code in
$F'$
-linear MRD code in
![]() $M_k(B)$
with minimum distance
$M_k(B)$
with minimum distance
![]() $k-l+1$
. In particular, if
$k-l+1$
. In particular, if
![]() $\textrm{deg}(h)=mn$
then
$\textrm{deg}(h)=mn$
then
![]() $S_{n,m,l}(\nu,\rho, f)$
defines an
$S_{n,m,l}(\nu,\rho, f)$
defines an
![]() $F'$
-linear MRD code in
$F'$
-linear MRD code in
![]() $M_n(E_{\hat{h}})$
with minimum distance
$M_n(E_{\hat{h}})$
with minimum distance
![]() $n-l+1$
.
$n-l+1$
.
Proof. We have to show that the minimum column rank of the matrix corresponding to a nonzero element in
![]() $S_{n,m,l}(\nu,\rho, f)$
is
$S_{n,m,l}(\nu,\rho, f)$
is
![]() $k-l+1$
. By Theorem 7, this is equivalent to finding an element
$k-l+1$
. By Theorem 7, this is equivalent to finding an element
![]() $g\in P$
such that the greatest common right divisor of
$g\in P$
such that the greatest common right divisor of
![]() $g$
and
$g$
and
![]() $h$
has degree at most
$h$
has degree at most
![]() $(l-1)m$
. Suppose towards a contradiction that
$(l-1)m$
. Suppose towards a contradiction that
![]() $\text{deg}(gcrd(g,h))=lm$
; since
$\text{deg}(gcrd(g,h))=lm$
; since
![]() $\text{deg}(g)\leq lm$
, it follows that
$\text{deg}(g)\leq lm$
, it follows that
![]() $g$
must be a divisor of
$g$
must be a divisor of
![]() $h$
.
$h$
.
As any divisor of
![]() $h$
is a product of irreducible polynomials similar to
$h$
is a product of irreducible polynomials similar to
![]() $f$
,
$f$
,
![]() $g$
must be a product of polynomials similar to
$g$
must be a product of polynomials similar to
![]() $f$
. This contradicts our assumption, so any matrix has rank at least
$f$
. This contradicts our assumption, so any matrix has rank at least
![]() $k-l+1$
.
$k-l+1$
.
7. Nuclei
Let
![]() $\mathcal{M}=\mathcal{M}(A)=\lbrace L_a \,|\,a\in A\rbrace \subseteq \textrm{End}_F(A)$
be the spread set of an
$\mathcal{M}=\mathcal{M}(A)=\lbrace L_a \,|\,a\in A\rbrace \subseteq \textrm{End}_F(A)$
be the spread set of an
![]() $F$
-algebra
$F$
-algebra
![]() $A$
, where
$A$
, where
![]() $L_a$
is the left multiplication map in
$L_a$
is the left multiplication map in
![]() $A$
. We define the left and right idealizers of
$A$
. We define the left and right idealizers of
![]() $\mathcal{M}$
as
$\mathcal{M}$
as
The centralizer of
![]() $\mathcal{M}$
is defined as
$\mathcal{M}$
is defined as
![]() $\textrm{Cent}(\mathcal{M})=\lbrace \Phi \in \textrm{End}_{F}(A)\,|\, \Phi M=M\Phi \quad \forall M\in \mathcal{M}\rbrace .$
We call
$\textrm{Cent}(\mathcal{M})=\lbrace \Phi \in \textrm{End}_{F}(A)\,|\, \Phi M=M\Phi \quad \forall M\in \mathcal{M}\rbrace .$
We call
![]() $Z(\mathcal{M})=I_l(\mathcal{M}) \cap \textrm{Cent}(\mathcal{M})$
the center of
$Z(\mathcal{M})=I_l(\mathcal{M}) \cap \textrm{Cent}(\mathcal{M})$
the center of
![]() $\mathcal{M}$
.
$\mathcal{M}$
.
Theorem 27 (cf. [Reference Sheekey34, Proposition 5] for finite fields). Let
![]() $A$
be a unital division algebra and
$A$
be a unital division algebra and
![]() $\mathcal{M}$
be the spread set of
$\mathcal{M}$
be the spread set of
![]() $A$
. Let
$A$
. Let
![]() $\mathcal{M}^*$
be the spread set associated with the opposite algebra
$\mathcal{M}^*$
be the spread set associated with the opposite algebra
![]() $A^{op}$
. Then
$A^{op}$
. Then
The proof from [Reference Sheekey34] holds verbatim in our general setting.
The above results can now be applied to determine the nuclei and center of the non-unital algebras
![]() $S=S_{n,m,l}(\nu,\rho,f)$
.
$S=S_{n,m,l}(\nu,\rho,f)$
.
In the following, let
![]() $R=D[t;\;\sigma ]$
. We use the assumptions on
$R=D[t;\;\sigma ]$
. We use the assumptions on
![]() $D$
, respectively
$D$
, respectively
![]() $K$
, and
$K$
, and
![]() $\sigma$
from Section 6.
$\sigma$
from Section 6.
Let
![]() $f\in R$
be an irreducible monic polynomial of degree
$f\in R$
be an irreducible monic polynomial of degree
![]() $m$
, and let
$m$
, and let
![]() $h$
be the minimal central left multiple of
$h$
be the minimal central left multiple of
![]() $f$
. We assume throughout that
$f$
. We assume throughout that
![]() $f$
is not right-invariant, so that
$f$
is not right-invariant, so that
![]() $k\gt 1$
.
$k\gt 1$
.
Remark 28.
The algebras
![]() $S_{n,m,l}(0,\rho,f)$
are unital Petit algebras and hence have left nucleus
$S_{n,m,l}(0,\rho,f)$
are unital Petit algebras and hence have left nucleus
![]() $\textrm{Nuc}_m(S)=D$
, and their right nucleus
$\textrm{Nuc}_m(S)=D$
, and their right nucleus
![]() $\lbrace g\in R_m\mid fg\in Rf\rbrace$
is the eigenspace of
$\lbrace g\in R_m\mid fg\in Rf\rbrace$
is the eigenspace of
![]() $f$
. If
$f$
. If
![]() $S_{n,m,l}(0,\rho,f)$
is not associative, then
$S_{n,m,l}(0,\rho,f)$
is not associative, then
![]() $\{d\in D\,|\, dg=gd \text{ for all }g\in S\}$
is their center [Reference Petit26].
$\{d\in D\,|\, dg=gd \text{ for all }g\in S\}$
is their center [Reference Petit26].
Theorem 29.
Let
![]() $R=D[t;\;\sigma ]$
and
$R=D[t;\;\sigma ]$
and
![]() $\textrm{deg}(h)=dmn$
. Suppose
$\textrm{deg}(h)=dmn$
. Suppose
![]() $l\leq dn/2$
,
$l\leq dn/2$
,
![]() $n\gt 1$
and
$n\gt 1$
and
![]() $lm\gt 2$
. Let
$lm\gt 2$
. Let
![]() $S=S_{n,m,l}(\nu,\rho,f)$
and
$S=S_{n,m,l}(\nu,\rho,f)$
and
![]() $\mathcal{M}$
be the image of
$\mathcal{M}$
be the image of
![]() $S$
in
$S$
in
![]() $\textrm{End}_{E_f}(R/Rf)$
, that means the corresponding rank metric code lies in
$\textrm{End}_{E_f}(R/Rf)$
, that means the corresponding rank metric code lies in
![]() $M_n(E_{\hat{h}})$
. If
$M_n(E_{\hat{h}})$
. If
![]() $\nu \neq 0$
, we have
$\nu \neq 0$
, we have
-
(i)
 $I_l(\mathcal{M})\cong \lbrace g_0\in D \,|\, g_0\nu =\nu \rho ( g_0)\rbrace \subset D$
(in particular,
$I_l(\mathcal{M})\cong \lbrace g_0\in D \,|\, g_0\nu =\nu \rho ( g_0)\rbrace \subset D$
(in particular,
 $I_l(\mathcal{M})\cong \textrm{Fix}(\rho )$
if
$I_l(\mathcal{M})\cong \textrm{Fix}(\rho )$
if
 $\nu \in C$
),
$\nu \in C$
),
-
(ii)
 $I_r(\mathcal{M})\cong \textrm{Fix}(\rho ^{-1}\circ \sigma ^{lm})\subset D$
,
$I_r(\mathcal{M})\cong \textrm{Fix}(\rho ^{-1}\circ \sigma ^{lm})\subset D$
, -
(iii)
 $\textrm{Cent}(\mathcal{M})\cong E_{\hat{h}}$
,
$\textrm{Cent}(\mathcal{M})\cong E_{\hat{h}}$
,
 $Z(\mathcal{M}) \cong F'$
.
$Z(\mathcal{M}) \cong F'$
.
If
![]() $\nu =0$
, we have
$\nu =0$
, we have
-
(iv)
 $I_l(\mathcal{M})\cong D$
,
$I_l(\mathcal{M})\cong D$
,
 $I_r(\mathcal{M})\cong D$
,
$I_r(\mathcal{M})\cong D$
, -
(v)
 $\textrm{Cent}(\mathcal{M})\cong E_{\hat{h}}$
,
$\textrm{Cent}(\mathcal{M})\cong E_{\hat{h}}$
,
 $Z(\mathcal{M})\cong F$
.
$Z(\mathcal{M})\cong F$
.
Much of the proof works identically to the proof of [Reference Sheekey34, Theorem 9]. We sketch the proof to highlight the main differences in this more general case. The
![]() $lm=2$
case has to be considered separately, and we have only been able to solve that for
$lm=2$
case has to be considered separately, and we have only been able to solve that for
![]() $F=\mathbb{R}$
.
$F=\mathbb{R}$
.
Proof. Let
![]() $\mathcal{M}=\{L_a\in \textrm{End}_{E_f}(R/Rf)\,|\, a\in P\}$
be the image of
$\mathcal{M}=\{L_a\in \textrm{End}_{E_f}(R/Rf)\,|\, a\in P\}$
be the image of
![]() $S$
in
$S$
in
![]() $\textrm{End}_{E_f}(R/Rf)\subset \textrm{End}_{F}(R/Rf)$
. In the following, we identify each element in
$\textrm{End}_{E_f}(R/Rf)\subset \textrm{End}_{F}(R/Rf)$
. In the following, we identify each element in
![]() $\mathcal{M}$
with the element
$\mathcal{M}$
with the element
![]() $g\in S$
that induces it. Analogously to the proof of [Reference Sheekey34, Theorem 9],
$g\in S$
that induces it. Analogously to the proof of [Reference Sheekey34, Theorem 9],
![]() $\lbrace g\in I_l(\mathcal{M}) \,|\, \text{deg}(g)\leq lm\rbrace = \lbrace g_0\in D \,|\, g_0\nu =\nu \rho (g_0)\rbrace$
. If
$\lbrace g\in I_l(\mathcal{M}) \,|\, \text{deg}(g)\leq lm\rbrace = \lbrace g_0\in D \,|\, g_0\nu =\nu \rho (g_0)\rbrace$
. If
![]() $\nu =0$
, then
$\nu =0$
, then
![]() $1\in \mathcal{M}$
so
$1\in \mathcal{M}$
so
![]() $I_l(\mathcal{M})\subset \mathcal{M}$
so all
$I_l(\mathcal{M})\subset \mathcal{M}$
so all
![]() $g\in I_l(\mathcal{M})$
have degree at most
$g\in I_l(\mathcal{M})$
have degree at most
![]() $lm$
. Consider
$lm$
. Consider
![]() $\nu \neq 0$
. To check there are no elements
$\nu \neq 0$
. To check there are no elements
![]() $g\in I_l(\mathcal{M})$
of degree higher than
$g\in I_l(\mathcal{M})$
of degree higher than
![]() $lm$
, we follow the approach of [Reference Sheekey34, Theorem 9] and consider
$lm$
, we follow the approach of [Reference Sheekey34, Theorem 9] and consider
![]() $gt \text{ mod } \hat{h}(u^{-1}t^n)$
. Recalling
$gt \text{ mod } \hat{h}(u^{-1}t^n)$
. Recalling
![]() $\text{deg}(h)=dm$
, we have
$\text{deg}(h)=dm$
, we have
![]() $h(t)=(u^{-1}t^n)^{dm}+\dots = u^{-dm}(t^n+h'_{dm-1}t^{(dm-1)n}+\dots +h'_0)$
so
$h(t)=(u^{-1}t^n)^{dm}+\dots = u^{-dm}(t^n+h'_{dm-1}t^{(dm-1)n}+\dots +h'_0)$
so
 \begin{equation*}gt \text { mod } h(t)=\left (\sum _{i=0}^{dmn-1}g_{i-1}t^i\right )-g_{dmn-1}u^{dm}\left (\sum _{j=0}^{dm-1}h'_jt^{nj}\right ).\end{equation*}
\begin{equation*}gt \text { mod } h(t)=\left (\sum _{i=0}^{dmn-1}g_{i-1}t^i\right )-g_{dmn-1}u^{dm}\left (\sum _{j=0}^{dm-1}h'_jt^{nj}\right ).\end{equation*}
As
![]() $g\in I_l(\mathcal{M})$
, this implies
$g\in I_l(\mathcal{M})$
, this implies
![]() $gt \text{ mod } h\in \mathcal{M}$
, so for all
$gt \text{ mod } h\in \mathcal{M}$
, so for all
![]() $i\in \lbrace lm+1,\dots, dmn-1\rbrace$
, we have
$i\in \lbrace lm+1,\dots, dmn-1\rbrace$
, we have
 \begin{equation} g_{i-1}=\begin{cases} 0& \text{for } i\not \equiv 0\text{ mod }n\\ g_{dmn-1}u^{dm}h'_{i/n}& \text{for } i\equiv 0\text{ mod }n \end{cases} \end{equation}
\begin{equation} g_{i-1}=\begin{cases} 0& \text{for } i\not \equiv 0\text{ mod }n\\ g_{dmn-1}u^{dm}h'_{i/n}& \text{for } i\equiv 0\text{ mod }n \end{cases} \end{equation}
where
![]() $h'_{i/n}=0$
if
$h'_{i/n}=0$
if
![]() $i/n$
is not an integer. We will show that
$i/n$
is not an integer. We will show that
![]() $g_{dmn-1}=0$
and thus
$g_{dmn-1}=0$
and thus
![]() $\text{deg}(g)\leq lm-1$
. As
$\text{deg}(g)\leq lm-1$
. As
![]() $lm\gt 2$
, this follows verbatim from [Reference Sheekey34, Theorem 9].
$lm\gt 2$
, this follows verbatim from [Reference Sheekey34, Theorem 9].
The same holds for
![]() $I_r(\mathcal{M})$
following Sheekey’s proof with the appropriate amendments made for
$I_r(\mathcal{M})$
following Sheekey’s proof with the appropriate amendments made for
![]() $D[t;\;\sigma ]$
. The results for
$D[t;\;\sigma ]$
. The results for
![]() $\textrm{Cent}(\mathcal{M})$
and
$\textrm{Cent}(\mathcal{M})$
and
![]() $Z(\mathcal{M})$
hold verbatim from [Reference Sheekey34, Theorem 9].
$Z(\mathcal{M})$
hold verbatim from [Reference Sheekey34, Theorem 9].
Corollary 30.
Let
![]() $R=D[t;\;\sigma ]$
and
$R=D[t;\;\sigma ]$
and
![]() $\text{deg}(h)=dmn$
. Suppose
$\text{deg}(h)=dmn$
. Suppose
![]() $n\gt 1$
,
$n\gt 1$
,
![]() $m\gt 2$
and
$m\gt 2$
and
![]() $S=S_{n,m,1}(\nu,\rho,f)$
with
$S=S_{n,m,1}(\nu,\rho,f)$
with
![]() $\nu \neq 0$
be a division algebra. Then,
$\nu \neq 0$
be a division algebra. Then,
-
(i)
 $\textrm{Nuc}_l(S)\cong \lbrace g_0\in D \,|\, g_0\nu =\nu \rho ( g_0)\rbrace \subset D$
, so in particular
$\textrm{Nuc}_l(S)\cong \lbrace g_0\in D \,|\, g_0\nu =\nu \rho ( g_0)\rbrace \subset D$
, so in particular
 $\textrm{Nuc}_l(S)= \textrm{Fix}(\rho )\subset D$
, if
$\textrm{Nuc}_l(S)= \textrm{Fix}(\rho )\subset D$
, if
 $\nu \in C$
.
$\nu \in C$
. -
(ii)
 $\textrm{Nuc}_m(S)\cong \textrm{Fix}(\rho ^{-1}\circ \sigma ^{m})\subset D$
.
$\textrm{Nuc}_m(S)\cong \textrm{Fix}(\rho ^{-1}\circ \sigma ^{m})\subset D$
. -
(iii)
 $ C(S)= \textrm{Fix}(\rho )\cap F=F'$
.
$ C(S)= \textrm{Fix}(\rho )\cap F=F'$
. -
(iv)
 $\textrm{dim}_{F'}\textrm{Nuc}_r(S)=\textrm{dim}_{F'}(E_{\hat{h}})=\textrm{deg}(\hat{h})[F\;:\;F']=[F\;:\;F']dm$
.
$\textrm{dim}_{F'}\textrm{Nuc}_r(S)=\textrm{dim}_{F'}(E_{\hat{h}})=\textrm{deg}(\hat{h})[F\;:\;F']=[F\;:\;F']dm$
.
Theorem 31.
Let
![]() $R=K[t;\;\sigma ]$
and
$R=K[t;\;\sigma ]$
and
![]() $\textrm{deg}(h)=mn$
. Suppose
$\textrm{deg}(h)=mn$
. Suppose
![]() $l\leq n/2$
,
$l\leq n/2$
,
![]() $n\gt 1$
and
$n\gt 1$
and
![]() $lm\gt 2$
. Let
$lm\gt 2$
. Let
![]() $S=S_{n,m,l}(\nu,\rho,f)$
with
$S=S_{n,m,l}(\nu,\rho,f)$
with
![]() $\nu \neq 0$
and
$\nu \neq 0$
and
![]() $\mathcal{M}$
be the image of
$\mathcal{M}$
be the image of
![]() $S$
in
$S$
in
![]() $\textrm{End}_{E_f}(R/Rf)$
, so that the corresponding rank metric code lies in
$\textrm{End}_{E_f}(R/Rf)$
, so that the corresponding rank metric code lies in
![]() $M_n(E_{\hat{h}})$
. Then,
$M_n(E_{\hat{h}})$
. Then,
-
(i)
 $I_l(\mathcal{M})\cong \textrm{Fix}(\rho )\subset K$
,
$I_l(\mathcal{M})\cong \textrm{Fix}(\rho )\subset K$
,
 $I_r(\mathcal{M})\cong \textrm{Fix}(\rho ^{-1}\circ \sigma ^{lm})\subset K$
,
$I_r(\mathcal{M})\cong \textrm{Fix}(\rho ^{-1}\circ \sigma ^{lm})\subset K$
, -
(ii)
 $\textrm{Cent}(\mathcal{M})\cong E_{\hat{h}}$
,
$\textrm{Cent}(\mathcal{M})\cong E_{\hat{h}}$
,
 $Z(\mathcal{M})\cong F'$
. If
$Z(\mathcal{M})\cong F'$
. If
 $\nu =0$
, we have
$\nu =0$
, we have
-
(iii)
 $I_l(\mathcal{M})\cong K$
,
$I_l(\mathcal{M})\cong K$
,
 $I_r(\mathcal{M})\cong K$
,
$I_r(\mathcal{M})\cong K$
, -
(iv)
 $\textrm{Cent}(\mathcal{M})\cong E_{\hat{h}}$
,
$\textrm{Cent}(\mathcal{M})\cong E_{\hat{h}}$
,
 $Z(\mathcal{M})\cong F$
.
$Z(\mathcal{M})\cong F$
.
Again, the proof is analogous to the one of [Reference Sheekey34], Theorem 9 (it does not use the fact that for finite fields the right nucleus of
![]() $S_f$
is
$S_f$
is
![]() $E_{\hat{h}}$
, it only uses that
$E_{\hat{h}}$
, it only uses that
![]() $R/Rh$
has center
$R/Rh$
has center
![]() $E_{\hat{h}}$
).
$E_{\hat{h}}$
).
Corollary 32.
Let
![]() $R=K[t;\;\sigma ]$
and
$R=K[t;\;\sigma ]$
and
![]() $\textrm{deg}(h)=mn$
. Suppose that
$\textrm{deg}(h)=mn$
. Suppose that
![]() $n\gt 1$
,
$n\gt 1$
,
![]() $m\gt 2$
and that
$m\gt 2$
and that
![]() $S=(S(\nu,\rho,f),\circ )$
is a division algebra with
$S=(S(\nu,\rho,f),\circ )$
is a division algebra with
![]() $\nu \neq 0$
. Then,
$\nu \neq 0$
. Then,
-
(i)
 $\textrm{Nuc}_l(S)= \textrm{Fix}(\rho )\subset K$
,
$\textrm{Nuc}_l(S)= \textrm{Fix}(\rho )\subset K$
, -
(ii)
 $\textrm{Nuc}_m(S)= \textrm{Fix}(\rho ^{-1}\circ \sigma ^m)\subset K$
,
$\textrm{Nuc}_m(S)= \textrm{Fix}(\rho ^{-1}\circ \sigma ^m)\subset K$
, -
(iii)
 $ C(S)= \textrm{Fix}(\rho )\cap F=F'$
.
$ C(S)= \textrm{Fix}(\rho )\cap F=F'$
. -
(iv)
 $\textrm{ dim}_{F'}\textrm{Nuc}_r(S)=\textrm{ dim}_{F'}(E_{\hat{h}})=\textrm{deg}(\hat{h})[F\;:\;F']=[F\;:\;F']m$
.
$\textrm{ dim}_{F'}\textrm{Nuc}_r(S)=\textrm{ dim}_{F'}(E_{\hat{h}})=\textrm{deg}(\hat{h})[F\;:\;F']=[F\;:\;F']m$
.
Theorems 29, 31 and Corollaries 30, 32 generalize [Reference Sheekey34, Theorem 9, Corollary 1] which were proved for semifields.
8. Examples of division algebras and an MRD code when f(t) = t
 $^{\boldsymbol{{n}}}-\theta \in$
K[t;
$^{\boldsymbol{{n}}}-\theta \in$
K[t;
 $\sigma$
]
$\sigma$
]
8.1.
K = F(
 $\theta$
)
$\theta$
)
Let
![]() $K=F(\theta )$
be an extension of prime degree
$K=F(\theta )$
be an extension of prime degree
![]() $n$
. Let
$n$
. Let
![]() $f(t)=t^n-\theta \in K[t;\;\sigma ]$
. We now compute the rank metric code associated with the
$f(t)=t^n-\theta \in K[t;\;\sigma ]$
. We now compute the rank metric code associated with the
![]() $F'$
-algebra
$F'$
-algebra
![]() $S_{n,n,1}(\nu,\rho,f)$
. Note that
$S_{n,n,1}(\nu,\rho,f)$
. Note that
![]() $f(t) = t^3-\theta \in K[t;\;\sigma ]$
is irreducible if and only if
$f(t) = t^3-\theta \in K[t;\;\sigma ]$
is irreducible if and only if
![]() $\theta \not =\sigma ^{2}(z)\sigma (z)z$
for all
$\theta \not =\sigma ^{2}(z)\sigma (z)z$
for all
![]() $z\in K$
. If
$z\in K$
. If
![]() $F$
contains a primitive
$F$
contains a primitive
![]() $n$
th root of unity, then
$n$
th root of unity, then
![]() $f(t)$
is irreducible if and only if
$f(t)$
is irreducible if and only if
![]() $\theta \not =\sigma ^{n-1}(z)\cdots \sigma (z)z$
for all
$\theta \not =\sigma ^{n-1}(z)\cdots \sigma (z)z$
for all
![]() $z\in K$
.
$z\in K$
.
We assume that
![]() $f$
is irreducible. Define
$f$
is irreducible. Define
![]() $h(t)=(t^n-\theta )(t^n-\sigma (\theta ))\cdots (t^n-\sigma ^{n-1}(\theta ))=(t^n)^n+\dots +(\!-\!1)^nN_{K/F}(\theta ),$
then
$h(t)=(t^n-\theta )(t^n-\sigma (\theta ))\cdots (t^n-\sigma ^{n-1}(\theta ))=(t^n)^n+\dots +(\!-\!1)^nN_{K/F}(\theta ),$
then
![]() $h(t)=\textrm{mclm}(f)$
: as
$h(t)=\textrm{mclm}(f)$
: as
![]() $t^n-\sigma ^i(\theta )\in K[t^n]$
, the factors of
$t^n-\sigma ^i(\theta )\in K[t^n]$
, the factors of
![]() $h(t)$
all commute and
$h(t)$
all commute and
![]() $h(t)\in K[t^n]$
. Since
$h(t)\in K[t^n]$
. Since
![]() $\sigma (h(t))=(t^n-\sigma (\theta ))\cdots (t^n-\sigma ^{n-1}(\theta ))(t^n-\theta )=h(t),$
we know that
$\sigma (h(t))=(t^n-\sigma (\theta ))\cdots (t^n-\sigma ^{n-1}(\theta ))(t^n-\theta )=h(t),$
we know that
![]() $h(t)\in \textrm{Fix}(\sigma )[t]=F[t]$
so
$h(t)\in \textrm{Fix}(\sigma )[t]=F[t]$
so
![]() $h(t)\in F[t]\cap K[t^n]=F[t^n]=C(R)$
. Hence
$h(t)\in F[t]\cap K[t^n]=F[t^n]=C(R)$
. Hence
![]() $h(t)=\hat{h}(t^n)$
with
$h(t)=\hat{h}(t^n)$
with
![]() $\hat{h}(x)=x^n+(\!-\!1)^nN_{K/F}(\theta )\in F[x]$
. Thus
$\hat{h}(x)=x^n+(\!-\!1)^nN_{K/F}(\theta )\in F[x]$
. Thus
![]() $f$
divides
$f$
divides
![]() $h$
both from the left and the right by Lemma 1.
$h$
both from the left and the right by Lemma 1.
As
![]() $n$
is prime, the minimal central left multiple of
$n$
is prime, the minimal central left multiple of
![]() $f$
must have degree
$f$
must have degree
![]() $n$
in
$n$
in
![]() $F[x]$
by Theorem 3; thus,
$F[x]$
by Theorem 3; thus,
![]() $h(t)=\textrm{mclm}(f)$
, and hence,
$h(t)=\textrm{mclm}(f)$
, and hence,
![]() $\hat{h}(x)=x^n+(\!-\!1)^nN_{K/F}(\theta )$
also is an irreducible polynomial in
$\hat{h}(x)=x^n+(\!-\!1)^nN_{K/F}(\theta )$
also is an irreducible polynomial in
![]() $F[x]$
. As a field,
$F[x]$
. As a field,
![]() $E_f=\lbrace z+Rf \,|\, z\in F[t^n]\rbrace$
is generated by
$E_f=\lbrace z+Rf \,|\, z\in F[t^n]\rbrace$
is generated by
![]() $\lbrace 1+Rf,t^n+Rf,t^{2n}+Rf,\dots,t^{n(n-1)}+Rf\rbrace =\lbrace 1+Rf,\theta +Rf,\theta ^2+Rf,\dots,\theta ^{n-1}+Rf\rbrace$
over
$\lbrace 1+Rf,t^n+Rf,t^{2n}+Rf,\dots,t^{n(n-1)}+Rf\rbrace =\lbrace 1+Rf,\theta +Rf,\theta ^2+Rf,\dots,\theta ^{n-1}+Rf\rbrace$
over
![]() $F$
. As
$F$
. As
![]() $K$
is generated by
$K$
is generated by
![]() $\lbrace 1,\theta,\dots, \theta ^{n-1}\rbrace$
, there is a canonical isomorphism
$\lbrace 1,\theta,\dots, \theta ^{n-1}\rbrace$
, there is a canonical isomorphism
![]() $E_f\longrightarrow K$
,
$E_f\longrightarrow K$
,
![]() $x+Rf\mapsto x.$
$x+Rf\mapsto x.$
It is clear that
![]() $\lbrace 1+Rf,t+Rf,\dots,t^{n-1}+Rf\rbrace$
is an
$\lbrace 1+Rf,t+Rf,\dots,t^{n-1}+Rf\rbrace$
is an
![]() $E_f$
-basis for
$E_f$
-basis for
![]() $R/Rf$
. Let
$R/Rf$
. Let
![]() $a=a_0+a_1t+\dots +a_{n-1}t^{n-1}+\nu \rho (a_0)t^n\in S(\nu,\rho,h)$
. In order to determine
$a=a_0+a_1t+\dots +a_{n-1}t^{n-1}+\nu \rho (a_0)t^n\in S(\nu,\rho,h)$
. In order to determine
![]() $M_a$
, we consider how
$M_a$
, we consider how
![]() $L_{a_it^i}$
acts on the basis elements of
$L_{a_it^i}$
acts on the basis elements of
![]() $R/Rf$
. As left multiplication is distributive, i.e.
$R/Rf$
. As left multiplication is distributive, i.e.
![]() $L_{a+b}(x)=L_a(x)+L_b(x)$
, it follows that
$L_{a+b}(x)=L_a(x)+L_b(x)$
, it follows that
![]() $L_a=\sum _{i=0}^n L_{a_it^i},$
where
$L_a=\sum _{i=0}^n L_{a_it^i},$
where
![]() $a_n=\nu \rho (a_0)$
. For each
$a_n=\nu \rho (a_0)$
. For each
![]() $i$
, we have:
$i$
, we have:
 \begin{align*} L_{a_it^i}(1+Rf)=&a_it^i+Rf=(t^i+Rf)(\sigma ^{n-i}(a_i)+Rf)\\ L_{a_it^i}(t+Rf)=&a_it^{i+1}+Rf=(t^{i+1}+Rf)(\sigma ^{n-i-1}(a_i)+Rf)\\ \vdots & \qquad \qquad \qquad \qquad \vdots \\ L_{a_it^i}(t^{n-i}+Rf)=&a_it^n+Rf=a_i\theta +Rf=(1+Rf)(a_i\theta +Rf)\\ L_{a_it^i}(t^{n-i+1}+Rf)=&a_it^{n+1}+Rf=a_ix\theta +Rf=(t+Rf)(\sigma (a_i)\theta +Rf)\\ \vdots & \qquad \qquad \qquad \qquad \vdots \\ L_{a_it^i}(t^{n-1}+Rf)=&a_it^{i-1}\theta +Rf=(t^{i-1}+Rf)(\sigma ^{n-i+1}(a_i)\theta +Rf). \end{align*}
\begin{align*} L_{a_it^i}(1+Rf)=&a_it^i+Rf=(t^i+Rf)(\sigma ^{n-i}(a_i)+Rf)\\ L_{a_it^i}(t+Rf)=&a_it^{i+1}+Rf=(t^{i+1}+Rf)(\sigma ^{n-i-1}(a_i)+Rf)\\ \vdots & \qquad \qquad \qquad \qquad \vdots \\ L_{a_it^i}(t^{n-i}+Rf)=&a_it^n+Rf=a_i\theta +Rf=(1+Rf)(a_i\theta +Rf)\\ L_{a_it^i}(t^{n-i+1}+Rf)=&a_it^{n+1}+Rf=a_ix\theta +Rf=(t+Rf)(\sigma (a_i)\theta +Rf)\\ \vdots & \qquad \qquad \qquad \qquad \vdots \\ L_{a_it^i}(t^{n-1}+Rf)=&a_it^{i-1}\theta +Rf=(t^{i-1}+Rf)(\sigma ^{n-i+1}(a_i)\theta +Rf). \end{align*}
Thus, the matrix representing
![]() $L_{a_it^i}$
is given by
$L_{a_it^i}$
is given by
 \begin{equation*}M_{a_it^i}= \left ( \begin {array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 0 & 0 & \cdots & 0 & \sigma ^{n-i}(a_i)& 0 & \cdots & 0\\ 0 & 0 & \cdots & 0 &0 & \sigma ^{n-(i+1)}(a_i) & \cdots & 0\\ \vdots & & \ddots & & & & \ddots & \vdots \\ 0 & & & \ddots & & & & \sigma (a_{m})\\ a_i\theta & & & & & \ddots & & 0\\ 0 & \sigma ^{n-1}(a_i)\theta & & & & & & \\ \vdots & & \ddots & & & & \ddots & \vdots \\ 0 & 0 & \cdots & \sigma ^{n-(i-1)}(a_i)\theta & 0 & 0 & \cdots & 0\\ \end {array} \right ). \end{equation*}
\begin{equation*}M_{a_it^i}= \left ( \begin {array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 0 & 0 & \cdots & 0 & \sigma ^{n-i}(a_i)& 0 & \cdots & 0\\ 0 & 0 & \cdots & 0 &0 & \sigma ^{n-(i+1)}(a_i) & \cdots & 0\\ \vdots & & \ddots & & & & \ddots & \vdots \\ 0 & & & \ddots & & & & \sigma (a_{m})\\ a_i\theta & & & & & \ddots & & 0\\ 0 & \sigma ^{n-1}(a_i)\theta & & & & & & \\ \vdots & & \ddots & & & & \ddots & \vdots \\ 0 & 0 & \cdots & \sigma ^{n-(i-1)}(a_i)\theta & 0 & 0 & \cdots & 0\\ \end {array} \right ). \end{equation*}
As
![]() $M_a=\sum _{i=0}^nM_{a_it^i}$
, we obtain
$M_a=\sum _{i=0}^nM_{a_it^i}$
, we obtain
![]() $M_a=(m_{i,j})_{i,j}$
where
$M_a=(m_{i,j})_{i,j}$
where
 \begin{equation*} m_{i,j}=\begin {cases} \sigma ^{n+1-i}(a_0)+\sigma ^{n+1-i}(\nu \rho (a_0))\theta &\mbox {for } i=j,\\ \sigma ^{n+1-i}(a_{i-j}) &\mbox {for } i\gt j,\\ \sigma ^{n+1-i}(a_{n+i-j})\theta &\mbox {for } i\lt j. \end {cases} \end{equation*}
\begin{equation*} m_{i,j}=\begin {cases} \sigma ^{n+1-i}(a_0)+\sigma ^{n+1-i}(\nu \rho (a_0))\theta &\mbox {for } i=j,\\ \sigma ^{n+1-i}(a_{i-j}) &\mbox {for } i\gt j,\\ \sigma ^{n+1-i}(a_{n+i-j})\theta &\mbox {for } i\lt j. \end {cases} \end{equation*}
This yields
![]() $\mathcal{C}_{n,n,1}=\lbrace M_a\mid a_k\in K \mbox{ for } k=0,1,\dots,n-1\rbrace \subset M_n(K)$
as the matrix spread set of the
$\mathcal{C}_{n,n,1}=\lbrace M_a\mid a_k\in K \mbox{ for } k=0,1,\dots,n-1\rbrace \subset M_n(K)$
as the matrix spread set of the
![]() $n^2[F\;:\;F']$
-dimensional
$n^2[F\;:\;F']$
-dimensional
![]() $F'$
-algebra
$F'$
-algebra
![]() $S_{n,n,1}(\nu,\rho,f)$
. The algebra associated with this spread set is a division algebra if
$S_{n,n,1}(\nu,\rho,f)$
. The algebra associated with this spread set is a division algebra if
![]() $N_{K/F'}(\theta ) N_{K/F'}(\nu )\neq 1$
(Theorem 22). In that case, the spread set will be an MRD code. In particular, for
$N_{K/F'}(\theta ) N_{K/F'}(\nu )\neq 1$
(Theorem 22). In that case, the spread set will be an MRD code. In particular, for
![]() $\nu =0$
this condition is satisfied for any irreducible
$\nu =0$
this condition is satisfied for any irreducible
![]() $f(t)=t^n-\theta$
. This is the well known result that for irreducible
$f(t)=t^n-\theta$
. This is the well known result that for irreducible
![]() $f$
, the Petit algebra
$f$
, the Petit algebra
![]() $S_f$
is a division algebra and so are all its isotopes. For
$S_f$
is a division algebra and so are all its isotopes. For
![]() $n\gt 2$
and
$n\gt 2$
and
![]() $\nu \neq 0$
, Corollary 32 yields
$\nu \neq 0$
, Corollary 32 yields
8.2. Real division algebras of dimension 4
Over a finite field
![]() $F$
, all division algebras of dimension 4 over
$F$
, all division algebras of dimension 4 over
![]() $F$
which have
$F$
which have
![]() $F$
as their center and a nucleus of dimension 2 over
$F$
as their center and a nucleus of dimension 2 over
![]() $F$
can be constructed as algebras
$F$
can be constructed as algebras
![]() $S_{n,m,1}(\nu,\rho, f)$
for suitable parameters [Reference Sheekey34]. Let us now look at some real division algebras we obtain with our construction. If
$S_{n,m,1}(\nu,\rho, f)$
for suitable parameters [Reference Sheekey34]. Let us now look at some real division algebras we obtain with our construction. If
![]() $\nu =0$
, then any choice of an irreducible
$\nu =0$
, then any choice of an irreducible
![]() $f\in \mathbb{C}[t;\;\overline{\phantom{x}}]$
will yield an algebra isotopic to a real Petit division algebra. If
$f\in \mathbb{C}[t;\;\overline{\phantom{x}}]$
will yield an algebra isotopic to a real Petit division algebra. If
![]() $\nu \neq 0$
, any choice of irreducible
$\nu \neq 0$
, any choice of irreducible
![]() $f\in \mathbb{C}[t;\;\overline{\phantom{x}}]$
where
$f\in \mathbb{C}[t;\;\overline{\phantom{x}}]$
where
![]() $N_{\mathbb{C}/\mathbb{R}}(a_0)\not = 1/N_{\mathbb{C}/\mathbb{R}}(\nu )$
also yields a division algebra (Theorem 22).
$N_{\mathbb{C}/\mathbb{R}}(a_0)\not = 1/N_{\mathbb{C}/\mathbb{R}}(\nu )$
also yields a division algebra (Theorem 22).
Let
![]() $b\in \mathbb{R}$
and
$b\in \mathbb{R}$
and
![]() $f(t)=t^2-bi\in \mathbb{C}[t;\;\overline{\phantom{x}}]$
. Then,
$f(t)=t^2-bi\in \mathbb{C}[t;\;\overline{\phantom{x}}]$
. Then,
![]() $h(t)=\hat{h}(t^2)$
,
$h(t)=\hat{h}(t^2)$
,
![]() $\hat{h}(x)=x^2+b^2\in \mathbb{R}[x]$
, is the minimal central left multiple of
$\hat{h}(x)=x^2+b^2\in \mathbb{R}[x]$
, is the minimal central left multiple of
![]() $f$
, as
$f$
, as
![]() $h(t)=t^4+b^2=(t^2+bi)(t^2-bi).$
For all
$h(t)=t^4+b^2=(t^2+bi)(t^2-bi).$
For all
![]() $b\gt 0$
,
$b\gt 0$
,
![]() $f(t)=t^2-bi$
is irreducible in
$f(t)=t^2-bi$
is irreducible in
![]() $\mathbb{C}[t;\;\overline{\phantom{x}}]$
.
$\mathbb{C}[t;\;\overline{\phantom{x}}]$
.
For every irreducible
![]() $f(t)=t^2-bi$
, and
$f(t)=t^2-bi$
, and
![]() $\nu \in \mathbb{C}$
such that
$\nu \in \mathbb{C}$
such that
![]() $N_{\mathbb{C}/\mathbb{R}}(\nu )\neq \frac{1}{b^2},$
we obtain a four-dimensional real division algebra
$N_{\mathbb{C}/\mathbb{R}}(\nu )\neq \frac{1}{b^2},$
we obtain a four-dimensional real division algebra
![]() $S_{2,2,1}(\nu,\rho,f)$
and an MRD code given by its matrix spread set
$S_{2,2,1}(\nu,\rho,f)$
and an MRD code given by its matrix spread set
where
![]() $\rho$
is either the identity or the complex conjugation.
$\rho$
is either the identity or the complex conjugation.
As mentioned in Theorem 7, [Reference Sheekey34, Theorem 9] uses results to deal with the case when
![]() $lm=2$
that are valid over finite fields, but can be extended to
$lm=2$
that are valid over finite fields, but can be extended to
![]() $R=\mathbb{C}[t;\;\overline{\phantom{x}}]$
, for instance for
$R=\mathbb{C}[t;\;\overline{\phantom{x}}]$
, for instance for
![]() $f(t)=t^2-i$
:
$f(t)=t^2-i$
:
Theorem 33.
Let
![]() $f(t)=t^2-i\in \mathbb{C}[t;\;\overline{\phantom{x}}]$
. Suppose
$f(t)=t^2-i\in \mathbb{C}[t;\;\overline{\phantom{x}}]$
. Suppose
![]() $S=S_{2,2,1}(\nu,\rho,f)$
is a division algebra for some
$S=S_{2,2,1}(\nu,\rho,f)$
is a division algebra for some
![]() $\nu \neq 0$
and
$\nu \neq 0$
and
![]() $\rho \in \textrm{Aut}_{\mathbb{R}}(\mathbb{C})$
. Then,
$\rho \in \textrm{Aut}_{\mathbb{R}}(\mathbb{C})$
. Then,
-
(i)
 $\textrm{Nuc}_l(S)=\textrm{Nuc}_m(S)=\textrm{Fix}(\rho )$
,
$\textrm{Nuc}_l(S)=\textrm{Nuc}_m(S)=\textrm{Fix}(\rho )$
, -
(ii)
 $ C(S)=\mathbb{R}$
,
$ C(S)=\mathbb{R}$
, -
(iii)
 $\textrm{dim}_{\mathbb{R}}(\textrm{Nuc}_r(S))=\textrm{dim}_{\mathbb{R}}(\mathbb{R}[t^2])=2$
.
$\textrm{dim}_{\mathbb{R}}(\textrm{Nuc}_r(S))=\textrm{dim}_{\mathbb{R}}(\mathbb{R}[t^2])=2$
.
Proof. We have
![]() $h(t)=t^4+1\in \mathbb{R}[t^2]$
. Suppose
$h(t)=t^4+1\in \mathbb{R}[t^2]$
. Suppose
![]() $g+Rh\in I_l(\mathcal{M})$
for some
$g+Rh\in I_l(\mathcal{M})$
for some
![]() $g(t)=g_0+g_1t+g_2t^2+g_3t^3\in R$
. Then,
$g(t)=g_0+g_1t+g_2t^2+g_3t^3\in R$
. Then,
![]() $ga\in S(\nu,\rho,h)$
for all
$ga\in S(\nu,\rho,h)$
for all
![]() $a\in S$
. Direct and laborious computation yields
$a\in S$
. Direct and laborious computation yields
![]() $g_2=0$
,
$g_2=0$
,
![]() $g_3=-g_1\overline{\nu }$
, and
$g_3=-g_1\overline{\nu }$
, and
![]() $\nu \rho (g_0a_0+g_1\overline{\nu }\overline{a_1})=g_0\nu \rho (a_0)+g_1\overline{a_1}.$
This is satisfied for all
$\nu \rho (g_0a_0+g_1\overline{\nu }\overline{a_1})=g_0\nu \rho (a_0)+g_1\overline{a_1}.$
This is satisfied for all
![]() $a_0,a_1\in \mathbb{C}$
if and only if
$a_0,a_1\in \mathbb{C}$
if and only if
![]() $\nu \rho (g_0)=g_0\nu$
and
$\nu \rho (g_0)=g_0\nu$
and
![]() $g_1=\nu \rho (g_1\overline{\nu }).$
$g_1=\nu \rho (g_1\overline{\nu }).$
If
![]() $\rho =id$
, it follows that either
$\rho =id$
, it follows that either
![]() $g_1=0$
or
$g_1=0$
or
![]() $N_{\mathbb{C}/\mathbb{R}}(\nu )=1$
; as
$N_{\mathbb{C}/\mathbb{R}}(\nu )=1$
; as
![]() $S$
is a division algebra, Theorem 13 (or [Reference Sheekey34, Theorem 4]) forces
$S$
is a division algebra, Theorem 13 (or [Reference Sheekey34, Theorem 4]) forces
![]() $g_1=0$
and so
$g_1=0$
and so
![]() $g=g_0$
for some
$g=g_0$
for some
![]() $g_0\in \mathbb{C}$
. Thus
$g_0\in \mathbb{C}$
. Thus
![]() $I_l(\mathcal{M})=\mathbb{C}$
.If
$I_l(\mathcal{M})=\mathbb{C}$
.If
![]() $\rho =\overline{\phantom{x}}$
, then
$\rho =\overline{\phantom{x}}$
, then
![]() $g_1=\nu ^2g_1$
so either
$g_1=\nu ^2g_1$
so either
![]() $g_1=0$
or
$g_1=0$
or
![]() $\nu =\pm 1$
. As
$\nu =\pm 1$
. As
![]() $N_{\mathbb{C}/\mathbb{R}}(\nu )\neq 1$
[Reference Sheekey34, Theorem 4], this forces
$N_{\mathbb{C}/\mathbb{R}}(\nu )\neq 1$
[Reference Sheekey34, Theorem 4], this forces
![]() $g_1=0$
so
$g_1=0$
so
![]() $g=g_0$
for some
$g=g_0$
for some
![]() $g_0\in \mathbb{R}$
. In this case,
$g_0\in \mathbb{R}$
. In this case,
![]() $I_l(\mathcal{M})=\mathbb{R}$
.
$I_l(\mathcal{M})=\mathbb{R}$
.
The computations for
![]() $I_r(\mathcal{M})$
follow analogously and
$I_r(\mathcal{M})$
follow analogously and
![]() $\textrm{Cent}(\mathcal{M})$
and
$\textrm{Cent}(\mathcal{M})$
and
![]() $Z(\mathcal{M})$
follow from the proof of [Reference Sheekey34, Theorem 4]. We obtain the final result on the nuclei using Theorem 27 to relate the idealizers and centralizer of
$Z(\mathcal{M})$
follow from the proof of [Reference Sheekey34, Theorem 4]. We obtain the final result on the nuclei using Theorem 27 to relate the idealizers and centralizer of
![]() $\mathcal{M}$
to the nuclei of the algebra
$\mathcal{M}$
to the nuclei of the algebra
![]() $S$
.
$S$
.
Example 34.
If
![]() $f(t)=t^2-i$
, we obtain division algebras
$f(t)=t^2-i$
, we obtain division algebras
![]() $S$
for all
$S$
for all
![]() $\nu \in \mathbb{C}$
such that
$\nu \in \mathbb{C}$
such that
![]() $N_{\mathbb{C}/\mathbb{R}}(\nu )\neq 1.$
If
$N_{\mathbb{C}/\mathbb{R}}(\nu )\neq 1.$
If
![]() $\nu \neq 0$
and
$\nu \neq 0$
and
![]() $S$
is a division algebra, then
$S$
is a division algebra, then
![]() $ C(S)= \mathbb{R}$
and
$ C(S)= \mathbb{R}$
and
![]() $\textrm{dim}_{\mathbb{R}}\textrm{Nuc}_r(S)= 2.$
Since therefore
$\textrm{dim}_{\mathbb{R}}\textrm{Nuc}_r(S)= 2.$
Since therefore
![]() $\textrm{Nuc}_r(S)$
is a two-dimensional division algebra over
$\textrm{Nuc}_r(S)$
is a two-dimensional division algebra over
![]() $\mathbb{R}$
,
$\mathbb{R}$
,
![]() $\textrm{Nuc}_r(S)$
is an Albert isotope of
$\textrm{Nuc}_r(S)$
is an Albert isotope of
![]() $\mathbb{C}$
and can be found in the classification in [Reference Hübner and Petersson15, Theorem 1]: it must be
$\mathbb{C}$
and can be found in the classification in [Reference Hübner and Petersson15, Theorem 1]: it must be
![]() $ \mathbb{C}$
,
$ \mathbb{C}$
,
![]() $ \mathbb{C}^{(\overline{\phantom{x}},\overline{\phantom{x}})}$
,
$ \mathbb{C}^{(\overline{\phantom{x}},\overline{\phantom{x}})}$
,
![]() $ \mathbb{C}^{(1+L(v)\overline{\phantom{x}},\overline{\phantom{x}})}$
,
$ \mathbb{C}^{(1+L(v)\overline{\phantom{x}},\overline{\phantom{x}})}$
,
![]() $ \mathbb{C}^{(\overline{\phantom{x}}, 1+L(v)\overline{\phantom{x}})}$
, or
$ \mathbb{C}^{(\overline{\phantom{x}}, 1+L(v)\overline{\phantom{x}})}$
, or
![]() $ \mathbb{C}^{(1+L(v)\overline{\phantom{x}},1+L(w)\overline{\phantom{x}})}$
, with
$ \mathbb{C}^{(1+L(v)\overline{\phantom{x}},1+L(w)\overline{\phantom{x}})}$
, with
![]() $u,v\in \mathbb{C}$
suitably chosen.
$u,v\in \mathbb{C}$
suitably chosen.
If additionally
![]() $\rho =id$
, then
$\rho =id$
, then
![]() $\textrm{Nuc}_l(S) =\textrm{Nuc}_m(S)= \mathbb{C},$
and if
$\textrm{Nuc}_l(S) =\textrm{Nuc}_m(S)= \mathbb{C},$
and if
![]() $\rho =\overline{\phantom{x}}$
then
$\rho =\overline{\phantom{x}}$
then
![]() $\textrm{Nuc}_l(S)=\textrm{Nuc}_m(S)= \mathbb{R}.$
Note that the four-dimensional algebras in the first class are all isotopes of nonassociative quaternion algebras.
$\textrm{Nuc}_l(S)=\textrm{Nuc}_m(S)= \mathbb{R}.$
Note that the four-dimensional algebras in the first class are all isotopes of nonassociative quaternion algebras.
9. Constructing algebras and codes using irreducible f
 $\in$
R = D[t;
$\in$
R = D[t;
 $\delta$
]
$\delta$
]
We now consider the same construction using differential polynomial rings. Let
![]() $C$
a field of characteristic
$C$
a field of characteristic
![]() $p$
and
$p$
and
![]() $D$
be a finite-dimensional division algebra with center
$D$
be a finite-dimensional division algebra with center
![]() $C$
. Let
$C$
. Let
![]() $R=D[t;\;\delta ]$
, where
$R=D[t;\;\delta ]$
, where
![]() $\delta$
is a derivation of
$\delta$
is a derivation of
![]() $D$
, such that
$D$
, such that
![]() $\delta |_C$
is algebraic with minimum polynomial
$\delta |_C$
is algebraic with minimum polynomial
![]() $g(t)=t^{p^e}+c_1t^{p^{e-1}}+\dots + c_et\in F[t]$
of degree
$g(t)=t^{p^e}+c_1t^{p^{e-1}}+\dots + c_et\in F[t]$
of degree
![]() $p^e$
, with
$p^e$
, with
![]() $F=C\cap \textrm{Const}(\delta )$
. (This includes the special case where
$F=C\cap \textrm{Const}(\delta )$
. (This includes the special case where
![]() $d=1$
, that is
$d=1$
, that is
![]() $R=K[t;\;\delta ]$
, and
$R=K[t;\;\delta ]$
, and
![]() $\delta$
is an algebraic derivation with minimum polynomial
$\delta$
is an algebraic derivation with minimum polynomial
![]() $g$
.) Then,
$g$
.) Then,
![]() $g(\delta )=id_{d_0}$
is an inner derivation of
$g(\delta )=id_{d_0}$
is an inner derivation of
![]() $D$
. W.l.o.g. we choose
$D$
. W.l.o.g. we choose
![]() $d_0\in F$
, so that
$d_0\in F$
, so that
![]() $\delta (d_0)=0$
[Reference Jacobson18, Lemma 1.5.3]. Then,
$\delta (d_0)=0$
[Reference Jacobson18, Lemma 1.5.3]. Then,
![]() $C(D[t;\;\delta ]) = F[x]=\{\sum _{i=0}^{k}a_i(g(t)-d_0)^i\,|\, a_i\in F \}$
with
$C(D[t;\;\delta ]) = F[x]=\{\sum _{i=0}^{k}a_i(g(t)-d_0)^i\,|\, a_i\in F \}$
with
![]() $x=g(t)-d_0$
. The two-sided
$x=g(t)-d_0$
. The two-sided
![]() $f\in R$
are of the form
$f\in R$
are of the form
![]() $f(t)=uc(t)$
with
$f(t)=uc(t)$
with
![]() $u\in D$
and
$u\in D$
and
![]() $c(t)\in C(R)$
[Reference Jacobson18, Theorem 1.1.32]. All polynomials
$c(t)\in C(R)$
[Reference Jacobson18, Theorem 1.1.32]. All polynomials
![]() $f\in R$
are bounded.
$f\in R$
are bounded.
For every
![]() $f \in R$
, the minimal central left multiple of
$f \in R$
, the minimal central left multiple of
![]() $f$
in
$f$
in
![]() $R$
is the unique polynomial of minimal degree
$R$
is the unique polynomial of minimal degree
![]() $h \in C(R)=F[x]$
such that
$h \in C(R)=F[x]$
such that
![]() $h = gf$
for some
$h = gf$
for some
![]() $g \in R$
, and such that
$g \in R$
, and such that
![]() $h(t)=\hat{h}(g(t)-d_0)$
for some monic
$h(t)=\hat{h}(g(t)-d_0)$
for some monic
![]() $\hat{h}(x) \in F[x]$
. The bound
$\hat{h}(x) \in F[x]$
. The bound
![]() $f^*$
of
$f^*$
of
![]() $f$
is the unique minimal central left multiple of
$f$
is the unique minimal central left multiple of
![]() $f$
up to some scalar.
$f$
up to some scalar.
From now on, let
![]() $f \in R=D[t;\;\delta ]$
be a monic irreducible polynomial of degree
$f \in R=D[t;\;\delta ]$
be a monic irreducible polynomial of degree
![]() $m\gt 1$
and let
$m\gt 1$
and let
![]() $h(t)=\hat{h}(g(t)-d_0)$
be its minimal central left multiple. Then,
$h(t)=\hat{h}(g(t)-d_0)$
be its minimal central left multiple. Then,
![]() $\hat{h}(x)$
is irreducible in
$\hat{h}(x)$
is irreducible in
![]() $F[x]$
and
$F[x]$
and
![]() $h$
generates a maximal two-sided ideal
$h$
generates a maximal two-sided ideal
![]() $Rh$
in
$Rh$
in
![]() $R$
[Reference Jacobson18, p. 16]. We have
$R$
[Reference Jacobson18, p. 16]. We have
[Reference Ikehata17, Proposition 4], and
![]() $\textrm{deg}(h)=p^e deg(\hat{h})$
. Define
$\textrm{deg}(h)=p^e deg(\hat{h})$
. Define
![]() $E_{\hat{h}}=F[x]/F[x] \hat{h}(x)$
and let
$E_{\hat{h}}=F[x]/F[x] \hat{h}(x)$
and let
![]() $k$
be the number of irreducible factors of
$k$
be the number of irreducible factors of
![]() $h$
in
$h$
in
![]() $R$
.
$R$
.
Theorem 35 [Reference Owen23].
![]() $\textrm{Nuc}_r(S_f)$
is a central division algebra over
$\textrm{Nuc}_r(S_f)$
is a central division algebra over
![]() $E_{\hat{h}}$
of degree
$E_{\hat{h}}$
of degree
![]() $s=d p^e/k$
, and
$s=d p^e/k$
, and
In particular, this means that
![]() $\textrm{deg}(\hat{h})=\frac{dm}{s}$
,
$\textrm{deg}(\hat{h})=\frac{dm}{s}$
,
![]() $\textrm{deg}(h)=km=\frac{d p^e m}{s}$
, and
$\textrm{deg}(h)=km=\frac{d p^e m}{s}$
, and
Moreover,
![]() $s$
divides
$s$
divides
![]() $\textrm{gcd}(dm,d p^e)$
. If
$\textrm{gcd}(dm,d p^e)$
. If
![]() $f$
is not right-invariant, then
$f$
is not right-invariant, then
![]() $k\gt 1$
and
$k\gt 1$
and
![]() $s\not =d p^e$
.
$s\not =d p^e$
.
The proof is analogous to the one of Theorem 3. In particular,
![]() $[S_f\;:\;F]=[S_f\;:\;C] p^e =d^2 m\cdot p^e$
. Comparing dimensions, we obtain again that
$[S_f\;:\;F]=[S_f\;:\;C] p^e =d^2 m\cdot p^e$
. Comparing dimensions, we obtain again that
![]() $[S_f\;:\;\textrm{Nuc}_r(S_f)]=k$
, and if
$[S_f\;:\;\textrm{Nuc}_r(S_f)]=k$
, and if
![]() $f$
is not right-invariant,
$f$
is not right-invariant,
![]() $k\gt 1$
.
$k\gt 1$
.
For each
![]() $z(t)=\hat{z}(g(t)-d_0)\in F[g(t)-d_0]$
with
$z(t)=\hat{z}(g(t)-d_0)\in F[g(t)-d_0]$
with
![]() $\hat{z}\in F[x]$
, we have
$\hat{z}\in F[x]$
, we have
![]() $z\in Rf$
if and only if
$z\in Rf$
if and only if
![]() $z\in Rh$
. Let
$z\in Rh$
. Let
Together with the multiplication
![]() $(x+Rf)\circ (y+Rf)= (xy)+Rf$
for all
$(x+Rf)\circ (y+Rf)= (xy)+Rf$
for all
![]() $x,y\in F[(g(t)-d_0)]$
,
$x,y\in F[(g(t)-d_0)]$
,
![]() $E_f$
is a field extension of
$E_f$
is a field extension of
![]() $F$
of degree
$F$
of degree
![]() $\textrm{ deg }(\hat{h})$
isomorphic to
$\textrm{ deg }(\hat{h})$
isomorphic to
![]() $E_{\hat{h}}$
. Let
$E_{\hat{h}}$
. Let
![]() $B=\textrm{Nuc}_r(S_f)$
, then
$B=\textrm{Nuc}_r(S_f)$
, then
![]() $B$
has degree
$B$
has degree
![]() $s$
over
$s$
over
![]() $E_{\hat{h}}$
, and
$E_{\hat{h}}$
, and
![]() $R/Rf$
is a free right
$R/Rf$
is a free right
![]() $B$
-module of dimension
$B$
-module of dimension
![]() $k$
via
$k$
via
![]() $R/Rf\times B\longrightarrow R/Rf$
,
$R/Rf\times B\longrightarrow R/Rf$
,
![]() $(a+Rf)(z+Rf)=az+Rf$
. We assume
$(a+Rf)(z+Rf)=az+Rf$
. We assume
![]() $f$
is not right-invariant which yields
$f$
is not right-invariant which yields
![]() $k\gt 1$
.
$k\gt 1$
.
For
![]() $\rho \in \textrm{Aut}(D)$
define
$\rho \in \textrm{Aut}(D)$
define
![]() $F'=\textrm{Fix}(\rho )\cap F$
. We assume that
$F'=\textrm{Fix}(\rho )\cap F$
. We assume that
![]() $F/F'$
is finite-dimensional. Let
$F/F'$
is finite-dimensional. Let
![]() $\nu \in D$
and
$\nu \in D$
and
![]() $1\leq l\lt k=dp^e/s$
. Define the set
$1\leq l\lt k=dp^e/s$
. Define the set
![]() $S_{p^e,m,l}(\nu,\rho, f)=\lbrace a+Rh\,|\, a\in P\rbrace \subset R/Rh,$
where
$S_{p^e,m,l}(\nu,\rho, f)=\lbrace a+Rh\,|\, a\in P\rbrace \subset R/Rh,$
where
![]() $S_{p^e,m,l}(\nu,\rho, f)$
is a vector space over
$S_{p^e,m,l}(\nu,\rho, f)$
is a vector space over
![]() $F'$
of dimension
$F'$
of dimension
![]() $d^2 p^em[F\;:\;F']$
. We identify each element of
$d^2 p^em[F\;:\;F']$
. We identify each element of
![]() $S_{p^e,m,l}(\nu,\rho,f)$
with a map in
$S_{p^e,m,l}(\nu,\rho,f)$
with a map in
![]() $\textrm{End}_B(R/Rf)$
as follows: For each
$\textrm{End}_B(R/Rf)$
as follows: For each
![]() $a\in S_{p^e,m,l}(\nu,\rho,f)$
, let
$a\in S_{p^e,m,l}(\nu,\rho,f)$
, let
![]() $L_a\;:\;R/Rf\to R/Rf$
be the left multiplication map
$L_a\;:\;R/Rf\to R/Rf$
be the left multiplication map
![]() $L_a(b+Rf)=ab+Rf$
. Let
$L_a(b+Rf)=ab+Rf$
. Let
![]() $M_a$
be the matrix in
$M_a$
be the matrix in
![]() $M_k(B)$
representing
$M_k(B)$
representing
![]() $L_a$
with respect to a
$L_a$
with respect to a
![]() $B$
-basis of
$B$
-basis of
![]() $R/Rf$
and denote the image of
$R/Rf$
and denote the image of
![]() $S=S_{p^e,m,l}(\nu,\rho,f)$
in
$S=S_{p^e,m,l}(\nu,\rho,f)$
in
![]() $M_k(B)$
by
$M_k(B)$
by
For
![]() $l=1$
, this construction again yields algebras over
$l=1$
, this construction again yields algebras over
![]() $F'$
: define a multiplication on the
$F'$
: define a multiplication on the
![]() $F'$
-vector space
$F'$
-vector space
![]() $R_m=\lbrace g\in R \,|\, deg (g)\lt m\rbrace$
via
$R_m=\lbrace g\in R \,|\, deg (g)\lt m\rbrace$
via
For
![]() $m\gt 1$
,
$m\gt 1$
,
![]() $(R_m,\circ )$
is isomorphic to
$(R_m,\circ )$
is isomorphic to
![]() $S(\nu,\rho,f)=S_{p^e,m,1}(\nu,\rho,f)$
. Therefore, we also denote
$S(\nu,\rho,f)=S_{p^e,m,1}(\nu,\rho,f)$
. Therefore, we also denote
![]() $(R_m,\circ )$
by
$(R_m,\circ )$
by
![]() $S(\nu,\rho,f)=S_{p^e,m,1}(\nu,\rho,f)$
.
$S(\nu,\rho,f)=S_{p^e,m,1}(\nu,\rho,f)$
.
Example 36.
Let
![]() $R=D[t;\;\delta ]$
and
$R=D[t;\;\delta ]$
and
![]() $f(t)=t+c$
for some
$f(t)=t+c$
for some
![]() $c\in D$
. For
$c\in D$
. For
![]() $\nu \in D^\times$
and
$\nu \in D^\times$
and
![]() $\rho \in \textrm{Aut}(D)$
,
$\rho \in \textrm{Aut}(D)$
,
![]() $S_{p^e,1,1}(\nu,\rho,f)=(D,\circ )$
has the multiplication
$S_{p^e,1,1}(\nu,\rho,f)=(D,\circ )$
has the multiplication
for all
![]() $x,y\in D$
.
$x,y\in D$
.
Theorem 37.
Let
![]() $f\in D[t;\;\delta ]$
be irreducible and
$f\in D[t;\;\delta ]$
be irreducible and
![]() $\textrm{deg}(h)=km$
. For all
$\textrm{deg}(h)=km$
. For all
![]() $a+Rh\in R/Rh$
,
$a+Rh\in R/Rh$
,
In particular, if
![]() $\textrm{deg}(h)=dmp^e$
then
$\textrm{deg}(h)=dmp^e$
then
![]() $M_a\in M_{p^e}(E_{\hat{h}})$
and
$M_a\in M_{p^e}(E_{\hat{h}})$
and
Thus,
![]() $S_{p^e,m,1}(\nu,\rho,f)$
is a division algebra if and only if there are no divisors of
$S_{p^e,m,1}(\nu,\rho,f)$
is a division algebra if and only if there are no divisors of
![]() $h$
in
$h$
in
![]() $S_{p^e,m,1}(\nu,\rho,f)$
. More generally for
$S_{p^e,m,1}(\nu,\rho,f)$
. More generally for
![]() $l\gt 1$
, the above result means:
$l\gt 1$
, the above result means:
Theorem 38.
Suppose that
![]() $P$
does not contain any polynomial of degree
$P$
does not contain any polynomial of degree
![]() $lm$
, whose irreducible factors are all similar to
$lm$
, whose irreducible factors are all similar to
![]() $f$
. Then, the set
$f$
. Then, the set
![]() $S_{p^e,m,l}(\nu,\rho, f)$
defines an
$S_{p^e,m,l}(\nu,\rho, f)$
defines an
![]() $F'$
-linear MRD code in
$F'$
-linear MRD code in
![]() $M_k(B)$
with minimum distance
$M_k(B)$
with minimum distance
![]() $k-l+1$
. In particular, if
$k-l+1$
. In particular, if
![]() $\textrm{deg}(h)=dmp^e$
, then this code is an
$\textrm{deg}(h)=dmp^e$
, then this code is an
![]() $F'$
-linear MRD code in
$F'$
-linear MRD code in
![]() $M_{dp^e}(E_{\hat{h}})$
with minimum distance
$M_{dp^e}(E_{\hat{h}})$
with minimum distance
![]() $dp^e-l+1$
.
$dp^e-l+1$
.
Corollary 39.
Suppose that
![]() $l=1$
.
$l=1$
.
-
(i) If
 $a(t)+\nu \rho (a_0)t^m \in P$
is reducible, then
$a(t)+\nu \rho (a_0)t^m \in P$
is reducible, then
 $a(t)$
is not a left zero divisor of
$a(t)$
is not a left zero divisor of
 $(R_m,\circ )$
.
$(R_m,\circ )$
. -
(ii) If
 $\nu =0$
then
$\nu =0$
then
 $(R_m,\circ )$
is a division algebra over
$(R_m,\circ )$
is a division algebra over
 $F'$
, which for
$F'$
, which for
 $m\geq 2$
is a Petit algebra.
$m\geq 2$
is a Petit algebra.
-
(iii) If
 $P$
does not contain any polynomial similar to
$P$
does not contain any polynomial similar to
 $f$
, then
$f$
, then
 $(R_m,\circ )$
is a division algebra over
$(R_m,\circ )$
is a division algebra over
 $F'$
.
$F'$
.
The proofs are all identical to their analogues where
![]() $f\in D[t;\;\sigma ]$
.
$f\in D[t;\;\sigma ]$
.
Remark 40.
One can also use the reduced norm
![]() $N$
of the central simple algebra
$N$
of the central simple algebra
![]() $D(t;\;\delta )$
in this setting: given a central simple algebra
$D(t;\;\delta )$
in this setting: given a central simple algebra
![]() $D$
with a maximal subfield
$D$
with a maximal subfield
![]() $E$
and
$E$
and
![]() $R=D[t;\;\delta ]$
, take the ring of central quotients
$R=D[t;\;\delta ]$
, take the ring of central quotients
![]() $D(t;\;\delta )=\lbrace f/g\mid f\in R, g\in C(R)\rbrace$
of
$D(t;\;\delta )=\lbrace f/g\mid f\in R, g\in C(R)\rbrace$
of
![]() $R$
. It has center
$R$
. It has center
![]() $C(D(t;\;\delta ))=\textrm{Quot}(C(R))=F(x)$
, where
$C(D(t;\;\delta ))=\textrm{Quot}(C(R))=F(x)$
, where
![]() $x=g(t)=d_0$
. Let
$x=g(t)=d_0$
. Let
![]() $\tilde{\delta }$
be the extension of
$\tilde{\delta }$
be the extension of
![]() $\delta$
to
$\delta$
to
![]() $D(x)$
such that
$D(x)$
such that
![]() $\tilde{\delta }=id_{t\mid D(x)}$
. Then,
$\tilde{\delta }=id_{t\mid D(x)}$
. Then,
![]() $D(t;\;\delta )$
is a central simple
$D(t;\;\delta )$
is a central simple
![]() $F(x)$
-algebra, more precisely
$F(x)$
-algebra, more precisely
![]() $D(t;\;\delta )\cong (D(x),\tilde{\delta },d_0+x),$
i.e.
$D(t;\;\delta )\cong (D(x),\tilde{\delta },d_0+x),$
i.e.
![]() $D(t;\;\delta )$
is a generalized differential algebra.
$D(t;\;\delta )$
is a generalized differential algebra.
Let
![]() $N$
be the reduced norm of
$N$
be the reduced norm of
![]() $D(t;\;\delta )$
. For all
$D(t;\;\delta )$
. For all
![]() $f\in R$
,
$f\in R$
,
![]() $N(f)\in F[x]$
and
$N(f)\in F[x]$
and
![]() $f$
divides
$f$
divides
![]() $N(f)$
. Let
$N(f)$
. Let
![]() $\omega\;:\;D\to M_d(E)$
be the left regular representation of
$\omega\;:\;D\to M_d(E)$
be the left regular representation of
![]() $D$
. For any
$D$
. For any
![]() $f\in R$
of degree
$f\in R$
of degree
![]() $m$
,
$m$
,
![]() $N(f)=\pm \textrm{det}(\omega (a_m))^{p^e}x^{dm}+\dots .$
In particular,
$N(f)=\pm \textrm{det}(\omega (a_m))^{p^e}x^{dm}+\dots .$
In particular,
![]() $N(f)$
has degree
$N(f)$
has degree
![]() $dm$
[Reference Thompson and Pumplün36]. As the bound of
$dm$
[Reference Thompson and Pumplün36]. As the bound of
![]() $f$
has degree
$f$
has degree
![]() $dm$
in
$dm$
in
![]() $F[x]$
, it follows that
$F[x]$
, it follows that
![]() $N(f)$
is equal to the bound of
$N(f)$
is equal to the bound of
![]() $f$
. Thus if
$f$
. Thus if
![]() $\textrm{deg} (\hat{h})=dm$
, we conclude that
$\textrm{deg} (\hat{h})=dm$
, we conclude that
![]() $\hat{h}(x)=\pm N(f)$
.
$\hat{h}(x)=\pm N(f)$
.
There is more work to be done, for example, to determine the constant term of
![]() $N(f(t))$
. This may lead to criteria on how to obtain division algebras using our construction. Additionally, the nuclei of both the algebras and the codes need to be calculated. For instance, consider the special case where
$N(f(t))$
. This may lead to criteria on how to obtain division algebras using our construction. Additionally, the nuclei of both the algebras and the codes need to be calculated. For instance, consider the special case where
![]() $d=1$
, i.e.
$d=1$
, i.e.
![]() $R=K[t;\;\delta ]$
for some field extension
$R=K[t;\;\delta ]$
for some field extension
![]() $K/F$
. If
$K/F$
. If
![]() $f(t)=a_0+a_1t+\dots +a_mt^m\in R=K[t;\;\delta ]$
has degree
$f(t)=a_0+a_1t+\dots +a_mt^m\in R=K[t;\;\delta ]$
has degree
![]() $m$
, then
$m$
, then
![]() $N(f(t))=(\!-\!1)^{m(p^e-1)} a_m ^{p^e}x^m+\dots$
[Reference Thompson and Pumplün36, Thm 18(ii)] Thus,
$N(f(t))=(\!-\!1)^{m(p^e-1)} a_m ^{p^e}x^m+\dots$
[Reference Thompson and Pumplün36, Thm 18(ii)] Thus,
To find the constant term of
![]() $N(f)$
is difficult. It is possible to compute special cases though, for example, for
$N(f)$
is difficult. It is possible to compute special cases though, for example, for
![]() $f(t)=g(t)+a\in K[t;\;\delta ]$
,
$f(t)=g(t)+a\in K[t;\;\delta ]$
,
![]() $N(f(t))=(x+a)^{p^e}$
[Reference Thompson and Pumplün36].
$N(f(t))=(x+a)^{p^e}$
[Reference Thompson and Pumplün36].
Acknowledgement
We would like to thank J. Sheekey for several helpful discussions on the subject, and the referee, whose comments greatly improved our paper.