Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Werner, Dirk
1992.
New classes of Banach spaces which are M-ideals in their biduals.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 111,
Issue. 2,
p.
337.
Bierstedt, K. D.
and
Summers, W. H.
1993.
Biduals of weighted banach spaces of analytic functions.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 54,
Issue. 1,
p.
70.
Galbis, Antonio
1994.
Weighted Banach spaces of entire functions.
Archiv der Mathematik,
Vol. 62,
Issue. 1,
p.
58.
Blasco, Oscar
and
Galbis, Antonio
2001.
On Taylor Coefficients of Entire Functions Integrable against Exponential Weights.
Mathematische Nachrichten,
Vol. 223,
Issue. 1,
p.
5.
Boyd, Christopher
and
Rueda, Pilar
2006.
Complete weights andv-peak points of spaces of weighted holomorphic functions.
Israel Journal of Mathematics,
Vol. 155,
Issue. 1,
p.
57.
Wolf, Elke
2007.
The density condition and distinguishedness for weighted Fréchet spaces of holomorphic functions.
Journal of Mathematical Analysis and Applications,
Vol. 329,
Issue. 1,
p.
530.
Wolf, Elke
2008.
A characterization of weighted (LB)-spaces of holomorphic functions having the dual density condition.
Czechoslovak Mathematical Journal,
Vol. 58,
Issue. 3,
p.
741.
Wolf, Elke
2009.
Differences of weighted composition operators.
Collectanea mathematica,
Vol. 60,
Issue. 1,
p.
1.
Wolf, Elke
2011.
WEIGHTED COMPOSITION OPERATORS BETWEEN WEIGHTED BLOCH TYPE SPACES.
Mathematical Proceedings of the Royal Irish Academy,
Vol. 111,
Issue. -1,
p.
37.
Wolf, Elke
2011.
WEAKLY COMPACT DIFFERENCES OF (WEIGHTED) COMPOSITION OPERATORS.
Asian-European Journal of Mathematics,
Vol. 04,
Issue. 04,
p.
695.
Wegner, Sven-Ake
2011.
Projective limits of weighted LB-spaces of holomorphic functions.
Journal of Mathematical Analysis and Applications,
Vol. 383,
Issue. 2,
p.
409.
WOLF, ELKE
2012.
ORDER BOUNDED WEIGHTED COMPOSITION OPERATORS.
Journal of the Australian Mathematical Society,
Vol. 93,
Issue. 3,
p.
333.
Miralles, Alejandro
2012.
Schur spaces and weighted spaces of typeH∞.
Quaestiones Mathematicae,
Vol. 35,
Issue. 4,
p.
463.
Perfekt, Karl-Mikael
2013.
Duality and distance formulas in spaces defined by means of oscillation.
Arkiv för Matematik,
Vol. 51,
Issue. 2,
p.
345.
Miralles, Alejandro
and
Wolf, Elke
2013.
Hypercyclic composition operators on Hv0‐spaces.
Mathematische Nachrichten,
Vol. 286,
Issue. 1,
p.
34.
Wolf, Elke
2014.
Bellwethers of composition operators for typical-growth spaces.
Asian-European Journal of Mathematics,
Vol. 07,
Issue. 03,
p.
1450048.
Fernández, Julio C. Ramos
2016.
On the norm and the essential norm of weighted composition operators acting on the weighted Banach space of analytic functions.
Quaestiones Mathematicae,
Vol. 39,
Issue. 4,
p.
497.

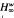 , respectively
, respectively 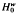 denote the Banach spaces of those entire functions φ(
denote the Banach spaces of those entire functions φ(