No CrossRef data available.
Article contents
Enriques surfaces and an Apollonian packing in eight dimensions
Published online by Cambridge University Press: 11 July 2022
Abstract
We call a packing of hyperspheres in n dimensions an Apollonian sphere packing if the spheres intersect tangentially or not at all; they fill the n-dimensional Euclidean space; and every sphere in the packing is a member of a cluster of 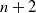 $n+2$ mutually tangent spheres (and a few more properties described herein). In this paper, we describe an Apollonian packing in eight dimensions that naturally arises from the study of generic nodal Enriques surfaces. The
$n+2$ mutually tangent spheres (and a few more properties described herein). In this paper, we describe an Apollonian packing in eight dimensions that naturally arises from the study of generic nodal Enriques surfaces. The 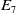 $E_7$,
$E_7$, 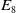 $E_8$ and Reye lattices play roles. We use the packing to generate an Apollonian packing in nine dimensions, and a cross section in seven dimensions that is weakly Apollonian. Maxwell described all three packings but seemed unaware that they are Apollonian. The packings in seven and eight dimensions are different than those found in an earlier paper. In passing, we give a sufficient condition for a Coxeter graph to generate mutually tangent spheres and use this to identify an Apollonian sphere packing in three dimensions that is not the Soddy sphere packing.
$E_8$ and Reye lattices play roles. We use the packing to generate an Apollonian packing in nine dimensions, and a cross section in seven dimensions that is weakly Apollonian. Maxwell described all three packings but seemed unaware that they are Apollonian. The packings in seven and eight dimensions are different than those found in an earlier paper. In passing, we give a sufficient condition for a Coxeter graph to generate mutually tangent spheres and use this to identify an Apollonian sphere packing in three dimensions that is not the Soddy sphere packing.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust


