Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T07:00:22.219Z Has data issue: false hasContentIssue false
  • English
  • Français

ESTIMATES FOR MARCINKIEWICZ INTEGRALS IN BMO AND CAMPANATO SPACES

Published online by Cambridge University Press:  09 August 2007

GUOEN HU ,
YAN MENG  and
DACHUN YANG
GUOEN HU
Affiliation:
Department of Applied Mathematics, University of Information Engineering, P. O. Box 1001-747, Zhengzhou 450002, People's Republic of China e-mail: huguoen@eyou.com
YAN MENG
Affiliation:
School of Information, Renmin University of China, Beijing 100872, People's Republic of China e-mail: mengyan@ruc.edu.cn
DACHUN YANG
Affiliation:
School of Mathematical Sciences, Beijing Normal University, Beijing 100875, People's Republic of China e-mail: dcyang@bnu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

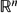In this paper, the authors consider the behavior on BMO() and Campanato spaces for the higher-dimensional Marcinkiewicz integral operator which is defined by where Ω is homogeneous of degree zero, has mean value zero and is integrable on the unit sphere. Under certain weak regularity condition on Ω, the authors prove that if f belongs to BMO() or to a certain Campanato space, then [μΩ(f)]2 is either infinite everywhere or finite almost everywhere, and in the latter case, some kind of boundedness is also obtained. The corresponding Lusin area integral is also considered.

Keywords

42B25
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 49 , Issue 2 , May 2007 , pp. 167 - 187
Copyright
Copyright © Glasgow Mathematical Journal Trust 2007

References

REFERENCES

1. Al-Salman, A., Al-Qassem, H., Cheng, L. C. and Pan, Y., Lp bounds for the function of Marcinkiewicz, Math. Res. Lett. 9 (2002), 697–700.Google Scholar
2. Campanato, S., Proprietà di hölderianitá di alcune classi di funzioni, Ann. Scuola Norm. Sup. Pisa (3) 17 (1963), 175–188.Google Scholar
3. Coifman, R. R. and Rochberg, R., Another characterization of BMO, Proc. Amer. Math. Soc. 79 (1980), 249–254.CrossRefGoogle Scholar
4. Ding, Y., Fan, D. and Pan, Y., Lp-boundedness of Marcinkiewicz integrals with Hardy space function kernels, Acta Math. Sin. (Engl. Ser.) 16 (2000), 593–600.CrossRefGoogle Scholar
5. Ding, Y., Lu, S. and Xue, Q., Marcinkiewicz integral on Hardy spaces, Integral Equations Operator Theory 42 (2002), 174–182.CrossRefGoogle Scholar
6. Ding, Y., Lu, S. and Xue, Q., On, Marcinkiewicz integral with homogeneous kernels, J. Math. Anal. Appl. 245 (2000), 471–488.CrossRefGoogle Scholar
7. Han, Y., On some properties of the s-function and the Marcinkiewicz integral (in Chinese), Beijing Daxue Xuebao 5 (1987), 21–34.Google Scholar
8. Janson, S., Taibleson, M. H. and Weiss, G., Elementary characterizations of the Morrey-Campanato spaces, in: Harmonic analysis (Cortona, 1982), Lecture Notes in Mathematics No. 992 (Springer-Verlag, 1983), 101–114CrossRefGoogle Scholar
9. John, F. and Nirenberg, L., On functions of bounded mean oscillation, Comm. Pure Appl. Math. 14 (1961), 415–426.CrossRefGoogle Scholar
10. Marcinkiewicz, J., Sur quelques intégrales du type de Dini, Ann. Soc. Polon. Math. 17 (1938), 42–50.Google Scholar
11. Fan, D. and Sato, S., Weak type (1,1) estimates for Marcinkiewicz integrals with rough kernels, Tohoku Math. J. (2) 53 (2001), 265–284.CrossRefGoogle Scholar
12. Leckband, M., A note on exponential integrability and pointwise estimates of Littlewood-Paley functions, Proc. Amer. Math. Soc. 109 (1990), 185–194.Google Scholar
13. Pérez, C. and Trujillo-González, R., Sharp weighted estimates for multilinear commutators, J. London Math. Soc. (2) 65 (2002), 672–692.CrossRefGoogle Scholar
14. Qiu, S., Boundedness of Littlewood-Paley operators and Marcinkiewicz integral on ceaz, p, J. Math. Res. Exposition 12 (1992), 41–50.Google Scholar
15. Sakamoto, M. and Yabuta, K., Boundedness of Marcinkiewicz functions, Studia Math. 135 (1999), 103–142.Google Scholar
16. Torchinsky, A. and Wang, S., A note on the Marcinkiewicz integral, Colloq. Math. 60/61 (1990), 235–243.CrossRefGoogle Scholar
17. Stein, E. M., On the functions of Littlewood-Paley, Lusin, and Marcinkiewicz, Trans. Amer. Math. Soc. 88 (1958), 430–466.CrossRefGoogle Scholar
18. Zygmund, A., On certain integrals, Trans. Amer. Math. Soc. 55 (1944), 170–204.CrossRefGoogle Scholar