Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T05:40:46.374Z Has data issue: false hasContentIssue false
  • English
  • Français

EXISTENCE OF INFINITELY MANY SOLUTIONS FOR SUBLINEAR ELLIPTIC PROBLEMS

Published online by Cambridge University Press:  30 March 2012

X. ZHONG  and
W. ZOU
X. ZHONG
Affiliation:
Department of Mathematical Sciences, Tsinghua University, Beijing 100084, China e-mail: zhongxuexiu1989@163.com
W. ZOU*
Affiliation:
Department of Mathematical Sciences, Tsinghua University, Beijing 100084, China e-mail: wzou@math.tsinghua.edu.cn
*
Corresponding author.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the following nonlinear Dirichlet boundary value problem: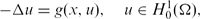 where Ω is a bounded domain in ℝN(N ≥ 2) with a smooth boundary ∂Ω and g ∈ C(Ω × ℝ) is a function satisfying 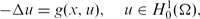for all x ∈ Ω. Under appropriate assumptions, we prove the existence of infinitely many solutions when g(x, t) is not odd in t.

Keywords

35J2035J2535J60
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 54 , Issue 3 , September 2012 , pp. 535 - 545
Copyright
Copyright © Glasgow Mathematical Journal Trust 2012

References

REFERENCES

1.Ambrosetti, A., Brezis, H. and Cerami, G., Combined effects of concave and convex nonlinearities in some elliptic problems, J. Funct. Anal. 122 (1994), 519–543.CrossRefGoogle Scholar
2.Ambrosetti, A. and Badiale, M., The dual variational principle and elliptic problems with discontinuous nonlinearities, J. Math. Anal. Appl. 140 (1989), 363–373.CrossRefGoogle Scholar
3.Bahri, A. and Berestycki, H., A perturbation method in critical point theory and applications, Trans. Amer. Math. Soc. 267 (1981) 1–31.CrossRefGoogle Scholar
4.Bartsch, T. and Willem, M., On an elliptic equations with convex and concave nonlinearties, Proc. Amer. Math. Soc. 123 (1995), 3555–3561.CrossRefGoogle Scholar
5.Chang, K. C., Infinite dimensional morse theory and multiple solution problems (Birkhäuser, 1993).CrossRefGoogle Scholar
6.Courant, R. and Hilbert, D., Methods of mathematical physics, Vol. I (Inerscience, New York, 1953).Google Scholar
7.Garcia Azorero, J. and Peral, I.Alonso, Multiplicity of solutions for elliptic problems with critical exponent or with a nonsymmetric term, Trans. Amer. Math. Soc. 323 (1991), 877–895.CrossRefGoogle Scholar
8.Hirano, N., Existence of infinitely many solutions for sublinear elliptic problems, J. Math. Anal. Appl. 218 (2003), 83–92.CrossRefGoogle Scholar
9.Kajikiya, R., Non-radial solutions with group invariance for the sublinear Emden-Fowler equation, Nonlinear Anal. 28 (2002), 567–597.Google Scholar
10.Spanier, E., Algebraic topology (McGraw-Hill, New York, 1966).Google Scholar
11.Wang, Z. Q., Nonlinear boundary value problems with concave nonlinearities near the origin, Nonlinear differ. equ. appl., 8 (2001) 15–33.CrossRefGoogle Scholar
12.Willem, M., Minimax theorems (Birkhäuser, 1996).CrossRefGoogle Scholar