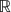Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ospanov, Kordan
2011.
Coercive estimates for a degenerate elliptic system of equations with spectral applications.
Applied Mathematics Letters,
Vol. 24,
Issue. 9,
p.
1594.
Hang, Trinh Thi Minh
and
Toan, Hoang Quoc
2011.
ON EXISTENCE OF WEAK SOLUTIONS OF NEUMANN PROBLEM FOR QUASILINEAR ELLIPTIC EQUATIONS INVOLVING p-LAPLACIAN IN AN UNBOUNDED DOMAIN.
Bulletin of the Korean Mathematical Society,
Vol. 48,
Issue. 6,
p.
1169.
Hang, Trinh Thi Minh
and
Toan, Hoang Quoc
2012.
EXISTENCE OF WEAK NON-NEGATIVE SOLUTIONS FOR A CLASS OF NONUNIFORMLY BOUNDARY VALUE PROBLEM.
Bulletin of the Korean Mathematical Society,
Vol. 49,
Issue. 4,
p.
737.
Hoang, Quoc Toan
and
Bui, Quoc Hung
2014.
ON A NEUMANN PROBLEM AT RESONANCE FOR NONUNIFORMLY SEMILINEAR ELLIPTIC SYSTEMS IN AN UNBOUNDED DOMAIN WITH NONLINEAR BOUNDARY CONDITION.
Bulletin of the Korean Mathematical Society,
Vol. 51,
Issue. 6,
p.
1669.
Hang, Trinh Thi Minh
and
Toan, Hoang Quoc
2014.
On Some Semilinear Nonuniformly Elliptic Problems with Subcritical Nonlinearity Without the Ambrosetti and Rabinowitz Condition.
Vietnam Journal of Mathematics,
Vol. 42,
Issue. 1,
p.
1.