Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T07:11:45.127Z Has data issue: false hasContentIssue false
  • English
  • Français

EXPLICIT CONSTRUCTION OF COMPANION BASES

Part of: Algebraic combinatorics Arithmetic rings and other special rings Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  21 July 2015

MARK JAMES PARSONS
MARK JAMES PARSONS*
Affiliation:
Institut für Mathematik und Wissenschaftliches Rechnen, Universität Graz Heinrichstraße 36, A-8010 Graz, Austria e-mail: mark.parsons@uni-graz.at
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A companion basis for a quiver Γ mutation equivalent to a simply-laced Dynkin quiver is a subset of the associated root system which is a 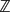$\mathbb{Z}$-basis for the integral root lattice with the property that the non-zero inner products of pairs of its elements correspond to the edges in the underlying graph of Γ. It is known in type A (and conjectured for all simply-laced Dynkin cases) that any companion basis can be used to compute the dimension vectors of the finitely generated indecomposable modules over the associated cluster-tilted algebra. Here, we present a procedure for explicitly constructing a companion basis for any quiver of mutation type A or D.

MSC classification

Primary: 13F60: Cluster algebras
Secondary: 05E10: Combinatorial aspects of representation theory 17B22: Root systems
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 58 , Issue 2 , May 2016 , pp. 357 - 384
Copyright
Copyright © Glasgow Mathematical Journal Trust 2015 

References

REFERENCES

1.Barot, M., Geiss, C. and Zelevinsky, A., Cluster algebras of finite type and positive symmetrizable matrices, J. London Math. Soc. 73 (3) (2006), 545–564.CrossRefGoogle Scholar
2.Barot, M. and Marsh, R., Reflection group presentations arising from cluster algebras, Trans. Amer. Math. Soc. 367 (2015), 1945–1967.Google Scholar
3.Bastian, J., Holm, T. and Ladkani, S., Derived equivalences for cluster-tilted algebras of Dynkin type D, J. Algebra. 410 (2014), 277–332.CrossRefGoogle Scholar
4.Buan, A., Marsh, R. and Reiten, I., Cluster-tilted algebras, Trans. Amer. Math. Soc. 359 (2007), 323–332.CrossRefGoogle Scholar
5.Buan, A., Marsh, R. and Reiten, I., Cluster mutation via quiver representations, Comment. Math. Helv. 83 (2) (2008), 143–177.Google Scholar
6.Buan, A., Marsh, R. and Reiten, I., Cluster-tilted algebras of finite representation type, J. Algebr. 306 (2) (2006), 412–431.Google Scholar
7.Buan, A. and Vatne, D., Derived equivalence classification for cluster-tilted algebras of type An, J. Algebr. 319 (7) (2008), 2723–2738.Google Scholar
8.Butler, M. C. R. and Ringel, C. M., Auslander-Reiten sequences with few middle terms and applications to string algebras, Comm. Algebr. 15 (1987), 145–179.Google Scholar
9.Caldero, P., Chapoton, F. and Schiffler, R., Quivers with relations arising from clusters (An case), Trans. Amer. Math. Soc. 358 (3) (2006), 1347–1364.Google Scholar
10.Caldero, P., Chapoton, F. and Schiffler, R., Quivers with relations and cluster-tilted algebras, Algebr. Represent. Theory 9 (4) (2006), 359–376.CrossRefGoogle Scholar
11.Derksen, H., Weyman, J. and Zelevinsky, A., Quivers with potentials and their representations I: Mutations, Sel. Math. (N.S.) 14 (1) (2008), 59–119.Google Scholar
12.Fomin, S. and Zelevinsky, A., Cluster algebras II: Finite type classification, Invent. Math. 154 (1) (2003), 63–121.Google Scholar
13.Nájera, A.Chávez, C-vectors and dimension vectors for cluster-finite quivers, Bull. London Math. Soc. 45 (3) (2013), 1259–1266.Google Scholar
14.Nakanishi, T. and Stella, S., Diagrammatic description of c-vectors and d-vectors of cluster algebras of finite type, Electron. J. Combin. 21 (1) (2014), #P1.3.Google Scholar
15.Parsons, M. J., On indecomposable modules over cluster-tilted algebras of type A, PhD Thesis (University of Leicester, 2007).Google Scholar
16.Parsons, M. J., Companion bases for cluster-tilted algebras, Algebr. Represent. Theory 17 (3) (2014), 775–808. doi:10.1007/s10468-013-9418-y.Google Scholar
17.Ringel, C. M., Cluster-concealed algebras, Adv. Math. 226 (2) (2011), 1513–1537.Google Scholar
18.Vatne, D. F., The mutation class of Dn quivers, Comm. Algebr. 38 (3) (2010), 1137–1146.Google Scholar