Published online by Cambridge University Press: 06 August 2021
In this paper, we characterize surjective isometries on certain classes of noncommutative spaces associated with semi-finite von Neumann algebras: the Lorentz spaces 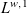 $L^{w,1}$
, as well as the spaces
$L^{w,1}$
, as well as the spaces 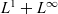 $L^1+L^\infty$
and
$L^1+L^\infty$
and 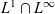 $L^1\cap L^\infty$
. The technique used in all three cases relies on characterizations of the extreme points of the unit balls of these spaces. Of particular interest is that the representations of isometries obtained in this paper are global representations.
$L^1\cap L^\infty$
. The technique used in all three cases relies on characterizations of the extreme points of the unit balls of these spaces. Of particular interest is that the representations of isometries obtained in this paper are global representations.