Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T16:17:22.813Z Has data issue: false hasContentIssue false
  • English
  • Français

EXTREME POINTS FOR COMBINATORIAL BANACH SPACES

Published online by Cambridge University Press:  27 July 2018

KEVIN BEANLAND ,
NOAH DUNCAN ,
MICHAEL HOLT  and
JAMES QUIGLEY
KEVIN BEANLAND
Affiliation:
Department of Mathematics, Washington and Lee University, Lexington, VA 24450. e-mail: beanlandk@wlu.edu, naduncan16@gmail.com, holtm11493@gmail.com, jamesbquigley93@gmail.com
NOAH DUNCAN
Affiliation:
Department of Mathematics, Washington and Lee University, Lexington, VA 24450. e-mail: beanlandk@wlu.edu, naduncan16@gmail.com, holtm11493@gmail.com, jamesbquigley93@gmail.com
MICHAEL HOLT
Affiliation:
Department of Mathematics, Washington and Lee University, Lexington, VA 24450. e-mail: beanlandk@wlu.edu, naduncan16@gmail.com, holtm11493@gmail.com, jamesbquigley93@gmail.com
JAMES QUIGLEY
Affiliation:
Department of Mathematics, Washington and Lee University, Lexington, VA 24450. e-mail: beanlandk@wlu.edu, naduncan16@gmail.com, holtm11493@gmail.com, jamesbquigley93@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A norm ‖ċ‖ on c00 is called combinatorial if there is a regular family of finite subsets 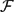$\mathcal{F}$, so that 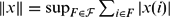$\|x\|=\sup_{F \in \mathcal{F}} \sum_{i \in F} |x(i)|$. We prove the set of extreme points of the ball of a combinatorial Banach space is countable. This extends a theorem of Shura and Trautman. The second contribution of this article is to exhibit many new examples of extreme points for the unit ball of dual Tsirelson's original space and give an explicit construction of an uncountable collection of extreme points of the ball of Tsirelson's original space. We also prove some stability properties of the intermediate norms used to define Tsirelson's space and give a lower bound of the stabilization function for these intermediate norms.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 61 , Issue 2 , May 2019 , pp. 487 - 500
Copyright
Copyright © Glasgow Mathematical Journal Trust 2018 

Footnotes

Noah Duncan, Michael Holt and James Quigley were undergraduate students at Washington and Lee University when the main results of this paper were obtained.

References

REFERENCES

1. Alspach, D. E. and Argyros, S. A., Complexity of weakly null sequences, Dissertationes Math. (Rozprawy Mat.), 321 (44) (1992).Google Scholar
2. Argyros, S. A. and Tolias, A., Methods in the theory of hereditarily indecomposable Banach spaces, Mem. Amer. Math. Soc. 170 (806) (2004), vi+114, 2004.Google Scholar
3. Aron, R. M. and Lohman, R. H., A geometric function determined by extreme points of the unit ball of a normed space, Pac. J. Math. 127 (2) (1987), 209–231.Google Scholar
4. Beanland, K. and Chu, H., The λ-property for combinatorial Banach spaces. Preprint.Google Scholar
5. Beanland, K., Duncan, N. and Holt, M., Time stopping for Tsirelson's norm. Involve 11 (5) (2018), 857–866.Google Scholar
6. Casazza, P. G. and Shura, T. J., Tsirel′son's space, Lecture notes in mathematics, vol. 1363 (Springer-Verlag, Berlin, 1989). With an appendix by Baker, J., Slotterbeck, O. and Aron, R..Google Scholar
7. Gasparis, I. and Leung, D. H., On the complemented subspaces of the Schreier spaces, Stud. Math. 141 (3) (2000), 273–300.Google Scholar
8. Lindenstrauss, J. and Phelps, R. R., Extreme point properties of convex bodies in reflexive Banach spaces, Isr. J. Math. 6 (1968), 39–48.Google Scholar
9. Shura, T. J. and Trautman, D., The λ-property in Schreier's space S and the Lorentz space d(a, 1), Glasg. Math. J. 32 (3) (1990), 277–284.Google Scholar
10. Tsirelson, B. S., It is impossible to imbed ℓp of c 0 into an arbitrary Banach space, Funkcional. Anal. Priložen 8 (2) (1974), 57–60.Google Scholar