Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-15T13:21:42.749Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite coverings by subgroups with a given property

Published online by Cambridge University Press:  18 May 2009

Marc A. Brodie  and
Luise-Charlotte Kappe
Marc A. Brodie
Affiliation:
Adirondack Community CollegeQueensbury, NY 12804-1498USA
Luise-Charlotte Kappe
Affiliation:
Suny at BinghamtonDepartment of Mathematical SciencesBinghamton, NY 13902-6000USA
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 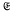be a group-theoretic property. We say a group has a finite covering by 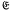-subgroups if it is the set-theoretic union of finitely many 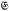-subgroups. The topic of this paper is the investigation of groups having a finite covering by nilpotent subgroups, n-abelian subgroups or 2-central subgroups.

R. Baer [12; 4.16] characterized central-by-finite groups as those groups having a finite covering by abelian subgroups. In [6] it was shown that [G: ZC (G)] finite implies the existence of a finite covering by subgroups of nilpotency class c, i.e. ℜc-groups. However, an example of a group is given there which has a finite covering by ℜ2-groups, but Z2(G) does not have finite index in the group. These results raise two questions, on which we will focus our investigations.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 35 , Issue 2 , May 1993 , pp. 179 - 188
Copyright
Copyright © Glasgow Mathematical Journal Trust 1993

References

REFERENCES

1.Baer, R., Endlichkeitskriterien für Kommutatorgruppen, Math. Annalen 124 (1952), 166–177.Google Scholar
2.Baer, R., Factorization of n-soluble and n-nilpotent groups, Proc. Amer. Math. Soc. 4 (1953), 15–26.Google Scholar
3.Brodie, M. A., Chamberlain, R. F. and Kappe, L. C., Finite coverings by normal subgroups, Proc. Amer. Math. Soc. 104 (1988), 669–674.CrossRefGoogle Scholar
4.Dietrich, A., Durch Einbettung beschriebene charakteristische Untergruppen, Diplomarbeit, Würzburg, 1990.Google Scholar
5.Hall, P., Verbal and Marginal Subgroups, J. Reine Angew. Math. 182 (1940), 156–157.CrossRefGoogle Scholar
6.Kappe, L. C., Finite coverings by 2-Engel groups, Bull. Austral. Math. Soc. 38 (1988), 141–150.CrossRefGoogle Scholar
7.Kappe, L. C. and Morse, R. F., Groups with 3-abelian normal closures, Arch. Math. 51 (1988), 104–110.CrossRefGoogle Scholar
8.Kappe, L. C. and Newell, M. L., On the n-centre of a group, Groups St. Andrews 1989, LMS Lecture Notes 160 (1991), 339–352.CrossRefGoogle Scholar
9.Neumann, B. H., Groups covered by finitely many cosets, Publ. Math. Debrecen 3 (1954), 227–242.CrossRefGoogle Scholar
10.Neumann, B. H., Groups covered by permutable subsets, J. London Math. Soc. 29 (1954), 236–248.CrossRefGoogle Scholar
11.Neumann, B. H., A problem of Paul Erdös on groups, J. Austral. Math. Soc. 21 A (1976), 467–472.CrossRefGoogle Scholar
12.Robinson, D. J. S., Finiteness conditions and generalized soluble groups, Part I, (Springer-Verlag 1972).CrossRefGoogle Scholar