Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ali, Asif
1998.
Groups ofp-length one for all primesp.
Communications in Algebra,
Vol. 26,
Issue. 9,
p.
2895.
Robinson, Derek J. S.
1999.
Algebra.
p.
171.
Robinson, Derek J. S.
1999.
Algebra.
p.
171.
Robinson, Derek J. S.
2001.
The structure of finite groups in which permutability is a transitive relation.
Journal of the Australian Mathematical Society,
Vol. 70,
Issue. 2,
p.
143.
Beidleman, J. C.
and
Heineken, H.
2003.
On the fitting core of a formation.
Bulletin of the Australian Mathematical Society,
Vol. 68,
Issue. 1,
p.
107.
Beidleman, James
Hauck, Peter
and
Heineken, Hermann
2004.
Totally permutable products of certain classes of finite groups.
Journal of Algebra,
Vol. 276,
Issue. 2,
p.
826.
Beidleman, James
and
Heineken, Hermann
2004.
Pairwise -connected Products of Certain Classes of Finite Groups.
Communications in Algebra,
Vol. 32,
Issue. 12,
p.
4741.
Beidleman, James C.
and
Heineken, Hermann
2010.
Fitting cores and supersolvable groups.
Ricerche di Matematica,
Vol. 59,
Issue. 2,
p.
319.
Ballester-Bolinches, Adolfo
Heineken, Hermann
and
Spagnuolo, Francesca
2017.
On Sylow permutable subgroups of finite groups.
Forum Mathematicum,
Vol. 29,
Issue. 6,
p.
1307.
Monakhov, Victor S.
and
Trofimuk, Alexander A.
2020.
On the supersolubility of a group with semisubnormal factors.
Journal of Group Theory,
Vol. 23,
Issue. 5,
p.
893.

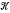 the class of finite groups that can be generated by subnormal
the class of finite groups that can be generated by subnormal 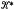 the subclass of
the subclass of 