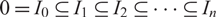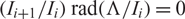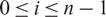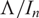Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zheng, Junling
2022.
The derived dimensions of (m,n)-Igusa-Todorov algebras.
Journal of Algebra,
Vol. 612,
Issue. ,
p.
227.